Continuamos la serie dedicada al álgebra geométrica con esta entrada, en la que seguiremos extrayendo consecuencias de los axiomas vistos hace dos entradas. Concretamente, después de haber visto el producto interior de dos vectores, examinaremos el producto exterior de dos vectores, que habíamos definido como la parte antisimétrica del producto geométrico de dos vectores. Veremos que el producto exterior de dos vectores no colineales no es ni escalar ni vector, sino un nuevo tipo de objeto del álgebra geométrica, un bivector simple.
El producto exterior de dos vectores no colineales no es un escalar
Según el axioma 3 de las álgebras geométricas (tenéis la exposición de los axiomas en esta entrada) el producto geométrico de un escalar con un vector siempre conmuta. Veamos pues si  conmuta con el vector
conmuta con el vector  . Si no conmuta, podremos descartar que el producto
exterior de vectores sea un escalar.[1].
. Si no conmuta, podremos descartar que el producto
exterior de vectores sea un escalar.[1].
Supongamos que tenemos dos vectores diferentes de  y no colineales, que nombramos
y no colineales, que nombramos  y
y  . Desarrollemos el producto siguiente:
. Desarrollemos el producto siguiente:
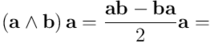
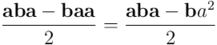
Veamos ahora el producto en orden inverso:
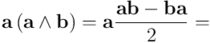
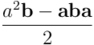
Comparando resultados, vemos que el producto geométrico del vector  con
con  cambia de signo al cambiar el orden del producto. La única forma de salvar la conmutatividad y que el primer producto pueda coincidir con el segundo es que ambos valgan
cambia de signo al cambiar el orden del producto. La única forma de salvar la conmutatividad y que el primer producto pueda coincidir con el segundo es que ambos valgan  . Pero no es difícil ver que eso sólo sucede cuando
. Pero no es difícil ver que eso sólo sucede cuando  se anula, o sea, cuando
se anula, o sea, cuando  y
y  son colineales.[2] Pero eso contradice nuestra suposición inicial,la de que partíamos de dos vectores no colineales.
son colineales.[2] Pero eso contradice nuestra suposición inicial,la de que partíamos de dos vectores no colineales.
Con ello queda claro que el producto exterior de dos vectores linealmente independientes no puede ser escalar.
El producto exterior de dos vectores tampoco puede ser un vector
El cuadrado de un vector, según el axioma 5b,[3] es un número real positivo. Comprobemos si el cuadrado del producto exterior  es positivo.
es positivo.
Primero volvamos a la identidad que expresa el producto geométrico de vectores como suma de producto interior y producto exterior:
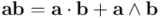
Si intercambio  con
con  , obtendré:
, obtendré:
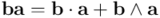
Teniendo en cuenta en la última igualdad que 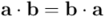 (por la simetría del producto interior de vectores) y que
(por la simetría del producto interior de vectores) y que 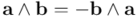 (por la antisimetría del producto exterior de vectores), la anterior igualdad queda así:
(por la antisimetría del producto exterior de vectores), la anterior igualdad queda así:
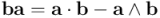
Bien, ahora calculemos el producto geométrico de  por
por  . Si calculamos directamente podríamos comenzar así:
. Si calculamos directamente podríamos comenzar así:
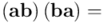
(siguiendo con la aplicación de la asociatividad del producto geométrico, el axioma 1)
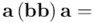
(dentro del paréntesis está el cuadrado de  , que por el axioma 5b, será un número real y positivo que llamaremos
, que por el axioma 5b, será un número real y positivo que llamaremos 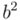 )
)
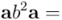
(como los reales conmutan con los vectores, según el axioma 3, podemos pasar 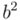 al principio y a continuación hacer el cuadrado de
al principio y a continuación hacer el cuadrado de  , que será el número real y positivo
, que será el número real y positivo 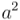 )
)
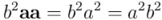
Pero, por otro lado, también podemos calcular 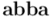 a partir de las expresiones en función de productos interiores y exteriores:
a partir de las expresiones en función de productos interiores y exteriores:
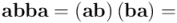
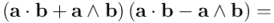
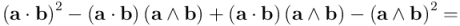
En la anterior expresión he utilizado, a la hora de escribir el tercer término, el hecho de que  es escalar y, por tanto, conmuta con
es escalar y, por tanto, conmuta con  . Por ello, el tercer término se anula con el segundo y tendremos finalmente este resultado:
. Por ello, el tercer término se anula con el segundo y tendremos finalmente este resultado:
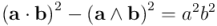
Recordemos ahora que el producto interior de dos vectores, en función del ángulo que forman entre ellos y de sus normas es: 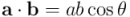 . Sustituyendo en el resultado anterior:
. Sustituyendo en el resultado anterior:

Finalmente, despejemos 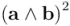 :
:

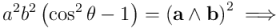
Y aquí aplicamos un fórmula fundamental de trigonometría: 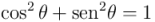 , de la que se deduce
, de la que se deduce 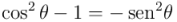 , y por tanto:
, y por tanto:

Vemos, pues, que el cuadrado del producto exterior de dos vectores, cuando es diferente de  (cosa que pasa si y sólo si los vectores son linealmente independientes), es negativo: el último miembro de la igualdad es un producto de cuadrados de números reales con un signo menos por delante. Esto quiere decir que el producto exterior de dos vectores no puede ser un vector, ya que estaría en contradicción con el axioma 5b.
(cosa que pasa si y sólo si los vectores son linealmente independientes), es negativo: el último miembro de la igualdad es un producto de cuadrados de números reales con un signo menos por delante. Esto quiere decir que el producto exterior de dos vectores no puede ser un vector, ya que estaría en contradicción con el axioma 5b.
Pero para mí, como físico, el argumento más contundente (sobre todo porque no necesita suponer el axioma 5b y métricas euclídeas)
de que  no es un vector es la bilinealidad. Si multiplicamos los vectores por un número diferente de 1, por ejemplo 2 o 3, el resultado del producto exterior no queda multiplicado respectivamente por 2 o 3, sino respectivamente, por 4 o 9. Y si cambiamos
los vectores de signo, multiplicándolos por -1, lo que en Física se conoce como aplicar una transformación de paridad al espacio, el producto exterior no cambia de signo, no cambia su paridad, a diferencia de los vectores.
no es un vector es la bilinealidad. Si multiplicamos los vectores por un número diferente de 1, por ejemplo 2 o 3, el resultado del producto exterior no queda multiplicado respectivamente por 2 o 3, sino respectivamente, por 4 o 9. Y si cambiamos
los vectores de signo, multiplicándolos por -1, lo que en Física se conoce como aplicar una transformación de paridad al espacio, el producto exterior no cambia de signo, no cambia su paridad, a diferencia de los vectores.
Por otra parte, el hecho de que el cuadrado de un producto exterior de dos vectores sea negativo recuerda inmediatamente a los números imaginarios. Ya iremos viendo lo lejos que llega esta analogía. De momento, del mismo modo que la norma de un número imaginario es la raíz cuadrada de su cuadrado cambiado de signo (ya que el cuadrado cambiado de signo es precisamente el producto de un número imaginario por su conjugado), podemos definir la norma del producto exterior de dos vectores a partir del resultado que hemos obtenido antes:

Esta norma la podemos interpretar como el valor del área del paralelogramo que se puede construir con los vectores  y
y  , como se puede apreciar en la figura:
, como se puede apreciar en la figura:

El área S (sombreada en rosa) del paralelogramo de la figura es igual al producto de la longitud de una base del paralelogramo por la altura relativa a la base. Podemos tomar la norma del vector  como la longitud de la base del paralelogramo, y la longitud de la altura respecto a ella será la norma de
como la longitud de la base del paralelogramo, y la longitud de la altura respecto a ella será la norma de  . La componente del vector
. La componente del vector  paralela a
paralela a  , que se ha etiquetado como
, que se ha etiquetado como  , no influye en el valor del área del paralelogramo. El valor del producto exterior
, no influye en el valor del área del paralelogramo. El valor del producto exterior  tampoco depende de
tampoco depende de  . Como la norma del producto exterior coincide con el del área del paralelogramo, es lógico identificar el producto exterior de dos vectores con el área orientada del paralelogramo que forman. El sentido del ángulo se establece desde el primer vector hasta el segundo vector del producto exterior.
. Como la norma del producto exterior coincide con el del área del paralelogramo, es lógico identificar el producto exterior de dos vectores con el área orientada del paralelogramo que forman. El sentido del ángulo se establece desde el primer vector hasta el segundo vector del producto exterior.
Si tomamos 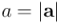 como la longitud de la base del paralelogramo, la respectiva altura del paralelogramo es
como la longitud de la base del paralelogramo, la respectiva altura del paralelogramo es 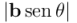 (la norma de la parte ortogonal de
(la norma de la parte ortogonal de  respecto a
respecto a  ,
,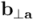 ). Por tanto, lo natural es aceptar que
). Por tanto, lo natural es aceptar que  no es un vector, sino un nuevo tipo de entidad, un bivector, más concretamente, un bivector simple.[4] Un bivector simple es un objeto del álgebra geométrica que representa una superficie orientada.
no es un vector, sino un nuevo tipo de entidad, un bivector, más concretamente, un bivector simple.[4] Un bivector simple es un objeto del álgebra geométrica que representa una superficie orientada.
Dos bivectores simples son iguales si representan la misma superficie orientada. Dos paralelogramos con la misma área, en planos paralelos y con la misma orientación (la orientación de un bivector simple cambia de signo al cambiar el orden del los vectores del producto exterior) representan un mismo bivector. De hecho, cualquier bivector simple se puede representar por una superficie orientada de cualquier forma. Puede servir un triángulo, un círculo o una elipse, por ejemplo.

En la figura vemos diferentes representaciones de un mismo bivector simple. Un bivector simple se puede entender como una área orientada. Los paralelogramos de la figura, así como la elipse, tienen todos ellos la misma área (si consideramos como base del paralelogramo el vector más largo, la altura de todos ellos es igual). Además, se encuentran en el mismo plano o en planos paralelos, La orientación del bivector la acaban de precisar las flechas verdes: se puede indicar con una flecha que va del primer vector del producto exterior hacia el segundo. También se puede indicar (y así no hace falta que el área tenga forma de paralelogramo) con una flecha curvada que de la vuelta al área orientada, de modo que cuando la flecha curva apunte en el mismo sentido que el primer vector del producto exterior cuando sea paralela a este, y que apunte en sentido contrario al segundo cuando le sea paralela. Si se cambia el sentido de la flecha verde, se entiende que el bivector representado cambia de signo (sería lo mismo que cambiar el orden del producto exterior).
En la figura, todas las áreas son iguales, tienen la misma orientación y representan por tanto el mismo bivector  . Si se cambia
. Si se cambia  por
por  , que resulta de sumar a
, que resulta de sumar a  un múltiplo escalar de
un múltiplo escalar de  , obtenemos un paralelogramo con la misma área orientada. También representarían el mismo bivector simple las mismas áreas si las hacemos rotar un ángulo cualquiera, siempre, eso sí, que se mantenga el plano original en que se encuentren.
, obtenemos un paralelogramo con la misma área orientada. También representarían el mismo bivector simple las mismas áreas si las hacemos rotar un ángulo cualquiera, siempre, eso sí, que se mantenga el plano original en que se encuentren.
Distributividad del producto exterior. Suma de bivectores simples contenidos en un espacio tridimensional
La distributividad del producto exterior de vectores respecto a la suma de vectores se deduce fácilmente a partir de la distributividad del producto geométrico. Recordemos antes la expresión fundamental:
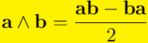
De ahí deducimos, por ejemplo, la distributividad por la derecha:
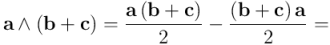

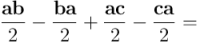
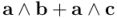
Así pues, tendremos:
Distributividad por la derecha:
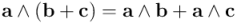
Distributividad por la izquierda:

En las expresiones de la distributividad del producto exterior, lo que tenemos es un bivector simple igualado a una suma de bivectores simples. En la figura siguiente podemos ver cómo la ley de distributividad da la clave para sumar bivectores simples contenidos en un espacio tridimensional.

En la parte izquierda de la figura se representa la suma de dos vectores. Fijémonos cómo se colocan los vectores a sumar de modo que la flecha que marca el extremo final de un vector entra por donde sale el extremo inicial del vector con el que se suma. En la parte derecha de la figura se indica la orientación de los bivectores simples con un circuito de flechas que va resiguiendo de cerca el contorno del bivector. Fijaos cómo la flecha del circuito asociado a cada bivector apunta siempre en el mismo sentido que la flecha del primer vector del producto exterior cuando pasa a su lado, y en sentido contrario al segundo vector del producto exterior cuando pasa a su lado (se puede comenzar a comprobar, por ejemplo, el bivector naranja:  ). Los bivectores simples que se suman (en naranja y rojo en la figura) se enganchan por un segmento (donde se puede superponer una copia del vector
). Los bivectores simples que se suman (en naranja y rojo en la figura) se enganchan por un segmento (donde se puede superponer una copia del vector  ) que es recorrido a cada lado por flechas que van en sentidos opuestos, en analogía con lo que pasa en el vértice del triángulo donde se enganchan los vectores sumandos en la parte izquierda de la figura.
) que es recorrido a cada lado por flechas que van en sentidos opuestos, en analogía con lo que pasa en el vértice del triángulo donde se enganchan los vectores sumandos en la parte izquierda de la figura.
Para obtener gráficamente la suma de dos bivectores simples en el espacio tridimensional tendremos, por tanto, que encontrar un factor común (en el caso de la figura, el vector  ), que será un vector contenido en la recta en que se cortan los planos de los respectivos bivectores simples, y reexpresar cada uno de los bivectores a multiplicar como producto exterior de ese vector factor común por otro vector. La ley de distributividad proporcionará el bivector simple que da el resultado de la suma. Encontrar un factor común siempre es posible en el caso de bivectores en el espacio tridimensional, pero no en general en el caso de espacios de cuatro o más dimensiones.[5]
), que será un vector contenido en la recta en que se cortan los planos de los respectivos bivectores simples, y reexpresar cada uno de los bivectores a multiplicar como producto exterior de ese vector factor común por otro vector. La ley de distributividad proporcionará el bivector simple que da el resultado de la suma. Encontrar un factor común siempre es posible en el caso de bivectores en el espacio tridimensional, pero no en general en el caso de espacios de cuatro o más dimensiones.[5]
Diferencia del producto exterior de vectores con el producto vectorial
Los que ya estáis habituados al producto vectorial de vectores reconoceréis el parecido con el producto vectorial: ambos productos representan la superficie orientada del paralelogramo construido con los factores, ambos productos cambian de signo al cambiar el orden de los factores, los dos son distributivos… Pero hay diferencias esenciales:
El producto vectorial es un vector que representa una superficie perpendicular a él. Eso sólo es posible en tres dimensiones, y limita el uso del producto vectorial a espacios de tres dimensiones. El producto exterior de dos vectores es, en cambio, un bivector, que ya es directamente una superficie orientada.

El producto exterior 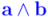 de dos vectores
de dos vectores  y
y  es una superficie orientada. El producto vectorial
es una superficie orientada. El producto vectorial  es un vector perpendicular a los dos vectores que se multiplican, y cuyo sentido se asigna con la regla de la mano derecha. Tanto la norma del producto exterior como la del producto vectorial dan el mismo valor numérico: el del área del paralelogramo construido a partir de los vectores
es un vector perpendicular a los dos vectores que se multiplican, y cuyo sentido se asigna con la regla de la mano derecha. Tanto la norma del producto exterior como la del producto vectorial dan el mismo valor numérico: el del área del paralelogramo construido a partir de los vectores  y
y  .
.
El producto exterior es, como veremos, asociativo:
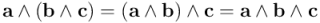
¿Y qué es el resultado de multiplicar exteriormente tres vectores? Veremos que es un trivector simple, el volumen orientado del paralelepípedo que tiene por aristas esos tres vectores.
El producto vectorial no es asociativo, ya que el resultado cambia según se multipliquen primero los dos primeros vectores o los dos últimos. En general se cumple:
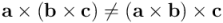
El primer miembro es un vector ortogonal a  que se encuentra en un plano que contiene simultáneamente los vectores
que se encuentra en un plano que contiene simultáneamente los vectores  y
y  . El segundo miembro de la desigualdad es un vector ortogonal a
. El segundo miembro de la desigualdad es un vector ortogonal a  que se encuentra en un plano que contiene simultáneamente los vectores
que se encuentra en un plano que contiene simultáneamente los vectores  y
y  . Excepcionalmente pueden coincidir, pero no en el caso general. En todo caso, ni uno ni otro se pueden relacionar con el volumen del paralelepípedo asociado a la tríada de vectores
. Excepcionalmente pueden coincidir, pero no en el caso general. En todo caso, ni uno ni otro se pueden relacionar con el volumen del paralelepípedo asociado a la tríada de vectores  ,
,  y
y  .
.
En álgebra geométrica evitaremos usar el producto vectorial. Recordemos que el producto exterior lo indicaremos con una cuña,  , y el producto vectorial con una aspa,
, y el producto vectorial con una aspa,  .
.
-
Sirve también comprobar si conmuta con el vector
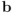 , o incluso un vector que sea una combinación lineal de los vectores
, o incluso un vector que sea una combinación lineal de los vectores  y
y 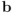 :
:  [↩]
[↩] -
Efectivamente, si
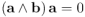 , podemos multiplicar por la derecha ambos lados de la igualdad por el inverso de
, podemos multiplicar por la derecha ambos lados de la igualdad por el inverso de  , que existe por ser el vector
, que existe por ser el vector  diferente de
diferente de 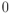 , y obtenemos inmediatamente
, y obtenemos inmediatamente 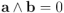 [↩]
[↩] -
Recordemos que este axioma se exige en el caso de métricas euclídeas. En el caso de métricas no euclídeas, como la de la relatividad especial, sí podemos tener vectores con cuadrado tanto positivo como negativo. [↩]
-
Ya veremos posteriormente en qué consiste la simplicidad de un multivector. De momento, sólo comentaré que, en todas las álgebras geométricas asociadas a espacios de tres dimensiones o menos, todos los bivectores son simples. [↩]
-
Esto está relacionado con la anterior nota al pie sobre la simplicidad de los multivectores, tema que queda para más adelante, como ya se indicaba allí. [↩]

The Explorando el álgebra geométrica 9 – El producto exterior de vectores y su interpretación geométrica by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.




{ 3 } Comentarios
La definición de producto geométrico no es coherente
La auténtica definición debe ser UV = -U.V +U^V
Así mismo U / V= 1/v² (U.V – U^V) que propicia la comprobación de dividendo=cociente por divisir. Lo que no ocurre en el otro caso. .
Hola José Manuel,
La definición que das se corresponde con la del producto de cuaterniones, a los que dediqué la tercera y cuarta entregas de esta serie sobre el álgebra geométrica. Allí vimos que los cuaterniones, que tienen cuatro componentes reales (que a su vez podemos agrupar en una componente escalar y tres componentes que forman lo que para Hamilton era un “vector”), tenían estructura de cuerpo no conmutativo (o más técnicamente quizás, anillo de división). Ello tiene como consecuencia que todo cuaternión no nulo tiene inverso y puede ser utilizado para dividir a otro cuaternión, usando la fórmula que das, y que yo apliqué en la última sección (Invertibilidad del producto de cuaterniones) del segundo capítulo dedicado a los cuaterniones.
En esa última sección de aquel capítulo ejemplifico precisamente a partir de la definición que das la invertibilidad del producto cuaterniónico. Pero una álgebra geométrica no es un cuerpo no conmutativo, como los cuaterniones, ya que un elemento genérico de una álgebra geométrica no sólo incluye parte escalar (parte real) y parte vectorial, sino que además puede incluir parte bivectorial, trivectorial… y hasta parte n-vectorial, donde n es la dimensión del espacio vectorial sobre el que se construye el álgebra vectorial que deseemos (puedes mirarte la décima entrega de la serie).
La definición de producto geométrico que doy es plenamente coherente, porque no pretendo definir un cuerpo multiplicativo (no conmutativo), sino un tipo de álgebra asociativa . El ejemplo típico y tópico de álgebra asociativa es la que forman las matrices cuadradas respecto a suma y producto de matrices entre sí, y al producto de números (reales o complejos) por las susodichas matrices. De hecho, cualquier álgebra asociativa es representable mediante una álgebra de matrices cuadradas, cosa que ha influido en la “obsesión” (si hemos de hacer caso a David Hestenes, gran promotor de la interpretación geométrica de las álgebras de Clifford) entre los físicos del pasado siglo por expresar diferentes álgebras geométricas mediante álgebras generadas por matrices (las matrices de Pauli, en el caso del álgebra geométrica del espacio euclídeo tridimensional, o las matrices de Dirac, en caso del álgebra asociada al espacio pseudoeuclídeo de cuadridimensional de la relatividad, cosa que contribuye a ocultar el significado geométrico subyacente). Recordemos que el inverso de una matriz no siempre existe: si la matriz tiene determinante nulo, no existe el inverso. En el álgebra geométrica no sólo contiene escalares y vectores, sino bivectores, trivectores y hasta n-vectores (donde n es la dimensionalidad del espacio vectorial sobre el que se construye). El producto de estos multivectores queda definido por los axiomas presentados en la séptima entrega de la serie. Por tanto, cuando digo que uv = u.v + u^v no estoy definiendo el producto geométrico en general, sólo me refiero al caso particular en que u y v son vectores: el resultado tiene una parte escalar (u.v) y otra bivectorial (u ^ v. El producto exterior de vectores, que represento con el símbolo ^, no es lo mismo que el producto vectorial, que represento con una aspa (x): el primero es asociativo, y da como resultado un bivector (cuando son dos los vectores multiplicados), el segundo da como resultado otro vector, pero no es asociativo.
Para que quede más claro, voy a rehacer a continuación, pero en el lenguaje del álgebra geométrica, el mismo ejemplo que puse al final de la cuarta entrega de la serie para ilustrar cómo la invertibilidad de los cuaterniones permitía encontrar dos vectores conociendo su producto escalar y su producto vectorial: allá sería como exactamente dices, supongo que estarás de acuerdo, porque está hecho con el lenguaje de los cuaterniones. Pero ahora voy a encontrar el vector incógnita a partir de su producto interior (que en el caso de vectores coincide con el producto escalar de vectores de toda la vida, y a la fecha en que escribo este comentario todavía no he llegado al capítulo en que defino el producto interior en el caso general) y de su producto exterior con otro vector conocido. Y verás que todo encajará perfectamente. Allá vamos:
Teníamos dos vectores v y w . El primero de ellos valía:
v = 6 i – 3 j + 2 k
Y nos piden encontrar w conociendo el producto escalar y vectorial de ambos:
v.w = -1
v x w = 13 i + 34 j + 12 k
Reescribamos ahora todo en el lenguaje del álgebra geométrica: los vectores i, j y k corresponden a los vectores e_1, e_2 y e_3:
v = 6 e_1 – 3 e_2 + 2 e_3
v . w = -1
Pero ojo al producto vectorial, que se transforma en producto exterior de esta forma:
v ^ w = 13 e_2 e_3 + 34 e_3 e_1 + 12 e_1 e_2
…porque v y w son vectores, y en cambio v ^ w es un bivector simple (no representa una longitud orientada, sino una área orientada). Escribimos e_2 e_3 en vez de e_2 ^ e_3 por comodidad, sencillamente porque el producto geométrico de dos vectores diferentes de una base ortogonal coincide con su producto exterior, por anularse el producto interior.
Pues bien, si conocemos el producto interior y el exterior de dos vectores, conocemos su producto geométrico, que será la suma formal de ambos:
v w = v . w + v . w =-1 + 13 e_2 e_3 + 34 e_3 e_1 + 12 e_1 e_2
Como el producto geométrico es asociativo, exactamente igual que el producto de matrices, y conocemos uno de los factores, tendremos forma de despejar w:
vw = ( 6 e_1 – 3 e_2 + 2 e_3 ) w = -1 + 13 e_2 e_3 + 34 e_3 e_1 + 12 e_1 e_2
Ya que como si de matrices se tratara, puedo multiplicar ambos miembros por v por la izquierda (no hace falta poner paréntesis en el producto geométrico de tres multivectores gracias a la asociatividad):
vvw = v (-1 + 13 e_2 e_3 + 34 e_3 e_1 + 12 e_1 e_2)
Y como el cuadrado de v sabemos que tiene que valer:
vv = (6 e_1 ? 3 e_2 + 2 e_3) (6 e_1 ? 3 e_2 + 2 e_3) = 6^2 + (-3)^2 + 2^2 = 36 + 9 + 4 = 49
Ya que el producto geométrico de un vector por sí mismo es escalar (no tiene parte vectorial, por el axioma de contracción) y queda expresado como suma de los cuadrados de sus componentes en la base ortonormal. Así pues, sustituimos en la fórmula anterior, que queda:
vvw = 49 w = (6 e_1 ? 3 e_2 + 2 e_3) (-1 + 13 e_2 e_3 + 34 e_3 e_1 + 12 e_1 e_2)
Ahora hacemos el producto geométrico en el miembro final antes de despejar w, como siempre, aplicando la asociatividad y recordando siempre que el cuadrado geométrico de un vector es un escalar (coincide con el producto interior del vector por s?? mismo) y que el producto geomérico de dos vectores ortogonales anticonmuta, por coincidir con su producto exterior:
49 w = 6 e_1 (-1) + 6 e_1 13 e_2 e_3 + 6 e_1 34 e_3 e_1 + 6 e_1 12 e_1 e_2 +
-3 e_2 (-1) – 3 e_2 13 e_2 e_3 – 3 e_2 34 e_3 e_1 – 3 e_2 12 e_1 e_2 +
+2 e_3 (-1) + 2 e_3 13 e_2 e_3 + 2 e_3 34 e_3 e_1 + 2 e_3 12 e_1 e_2
Efectuamos, pues, operaciones:
49 w = -6 e_1 + 78 e_1 e_2 e_3 – 204 e_3 + 72 e_2 +
+3 e_2 – 39 e_3 -102 e_1 e_2 e_3 + 36 e_1 +
= (-6 + 36 + 68) e_1 + (72 + 3 – 26) e_2 + (-204 – 39 – 2) e_3 + (78 – 102 + 24) e_1 e_2 e_3 =
= 98 e_1 + 49 e_ – 245 e_3 + 0 e_1 e_2 e_3
Vemos que en la versión en álgebra geométrica, el producto de vv por w es un vector, ya que la parte trivectorial (que es el volumen orientado del paralelepípedo de aristas v, v y w) se anula (en la versión con cuaterniones, lo que se anulaba era una parte escalar resultado de hacer un producto escalar de un vector con un producto vectorial de vectores: en los cuaterniones no sólo se “confunden” vectores con bivectores, sino además escalares con trivectores (que en álgebra geométrica asociada al espacio tridimensional son pseudoescalares, o sea, duales de escalares), lo que limita el uso de cuaterniones exclusivamente a la geometría tridimensional.
Finalmente puedo despejar w, aprovechando que el inverso de un escalar no nulo siempre existe:
w = 1/49 (98 e_1 + 49 e_2 – 245 e_3 ) = 2 e_1 + e_2 - 5 e_3
En plena concordancia con la versión “cuaterniónica” vista entonces, que sería lo que conoces. Espero haberte convencido de forma definitiva de que la definición de producto geométrico ??s absolutamente coherente…
Impresionante, Juan.
Qué gozada leerte.
Abrazos
Mac
Escribe un comentario