En esta entrada introduciré el concepto de base ortonormal, que hasta ahora no habíamos visto dentro del contexto del álgebra geométrica que estamos explorando en esta serie. A partir de la base ortonormal de vectores se construirá una base canónica de todos los multivectores del álgebra geométrica. El uso de bases ortonormales nos permitirá hacer cómputos de forma práctica en álgebra geométrica, facilitará la introducción de nuevos conceptos y permitirá avanzar de forma más directa.
Por otro lado, el abuso de las bases ortonormales conduce con demasiada frecuencia a pensar en los vectores como una “lista ordenada de coordenadas” en vez de una entidad matemática tan fundamental como los números reales o los complejos. No saber trabajar con magnitudes vectoriales o multivectoriales sin tener que recurrir siempre a descomponerlos en componentes es una muestra de limitación conceptual que lastra frecuentemente a los estudiantes, y sobre la que desde el principio han llamado la atención todos los proponentes del álgebra geométrica. Voy, pues, a introducir las bases ortonormales y aprovecharé para introducir más rápidamente nuevos conceptos, pero conviene no olvidar que los vectores, y los multivectores del álgebra geométrica en general, no deben concebirse como una simple lista de componentes expresadas en una cierta base.
Antes que nada, repasemos unos conceptos básicos de álgebra lineal.
Combinación lineal de vectores
Se dice que un vector  es combinación lineal de los m vectores
es combinación lineal de los m vectores  ,
, …
…  cuando podemos expresar el vector
cuando podemos expresar el vector  como suma de múltiplos escalares de los vectores
como suma de múltiplos escalares de los vectores  ,
,  …
…  :
:

El la figura siguiente se muestra un caso en que es posible expresar un vector como combinación lineal de vectores de más de una manera:

Vector expresado como combinación lineal de otros tres, en dos dimensiones. La figura muestra un vector  como combinación lineal de los tres vectores
como combinación lineal de los tres vectores  ,
,  y
y  , que se representan con flechas gruesas negras. Todos los vectores se suponen dentro de un mismo plano. De hecho, se muestran dos combinaciones lineales diferentes de
, que se representan con flechas gruesas negras. Todos los vectores se suponen dentro de un mismo plano. De hecho, se muestran dos combinaciones lineales diferentes de  ,
,  y
y  que producen el mismo vector
que producen el mismo vector  .
.
Independencia lineal de vectores
Un conjunto de m vectores  ,
,  …
…  es linealmente independiente si es imposible expresar cualquiera de ellos como combinación lineal de los demás o, de forma equivalente, si la única forma de obtener el vector
es linealmente independiente si es imposible expresar cualquiera de ellos como combinación lineal de los demás o, de forma equivalente, si la única forma de obtener el vector  como combinación lineal de los vectores
como combinación lineal de los vectores  ,
, …
…  es que todos los correspondientes factores
es que todos los correspondientes factores  ,
,  …
…  valgan
valgan  , es decir, la combinación lineal trivial que siempre proporciona el vector
, es decir, la combinación lineal trivial que siempre proporciona el vector  . Expresado formalmente:
. Expresado formalmente:

Siguiendo con el ejemplo de la figura anterior, los tres vectores  ,
,  y
y  no son linealmente independientes. La pista la da el hecho de poder expresar el vector
no son linealmente independientes. La pista la da el hecho de poder expresar el vector  con más de una combinación lineal. Tenemos por un lado:
con más de una combinación lineal. Tenemos por un lado:

y por otro:

Restemos las dos expresiones:

Es decir:

Con lo cual hemos obtenido 0 como combinación lineal no trivial.[1] Por lo tanto, los vectores  ,
,  y
y  no son linealmente independientes. Esto quiere decir que podemos expresar alguno de ellos en función de los demás. En este caso, podría ser cualquiera de los tres, pero es fácil decidirse por
no son linealmente independientes. Esto quiere decir que podemos expresar alguno de ellos en función de los demás. En este caso, podría ser cualquiera de los tres, pero es fácil decidirse por  :
:

Sustituyendo la expresión anterior en cualquiera de las combinaciones lineales que teníamos para expresar el vector  , obtendremos
, obtendremos  como combinación lineal de sólo dos vectores:
como combinación lineal de sólo dos vectores:  y
y  . ¿Son los vectores
. ¿Son los vectores  y
y  linealmente independientes? No cuesta mucho ver que sí lo son: si fueran linealmente dependientes, podríamos expresar uno como múltiplo real del otro, y sólo podríamos generar por combinación lineal vectores una familia de vectores paralelos.
linealmente independientes? No cuesta mucho ver que sí lo son: si fueran linealmente dependientes, podríamos expresar uno como múltiplo real del otro, y sólo podríamos generar por combinación lineal vectores una familia de vectores paralelos.
Base de un espacio vectorial
Se dice conjunto de n vectores linealmente independientes  ,
, …
…  forma una base de un espacio vectorial si cualquier vector
forma una base de un espacio vectorial si cualquier vector  del espacio vectorial se puede expresar como combinación lineal de los vectores
del espacio vectorial se puede expresar como combinación lineal de los vectores  ,
, …
…  . De la independencia lineal de estos n vectores se deduce que esta combinación lineal es única. Si hubiera dos maneras diferentes de expresar el vector
. De la independencia lineal de estos n vectores se deduce que esta combinación lineal es única. Si hubiera dos maneras diferentes de expresar el vector  como combinación lineal de los vectores
como combinación lineal de los vectores 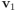 ,
, …
…  , por ejemplo así:
, por ejemplo así:

Podríamos hacer entonces como en el ejemplo propuesto y restar la segunda forma de expresar  de la primera, quedándonos esto:
de la primera, quedándonos esto:
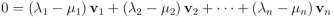
Si cada diferencia  la rebautizamos como
la rebautizamos como  , tendremos:
, tendremos:

Y como suponemos que partíamos de dos combinaciones lineales diferentes, no todos los números  ,
,  …
…  pueden ser a la vez iguales a
pueden ser a la vez iguales a 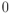 . Pero eso es una contradicción, porque significa que los n vectores
. Pero eso es una contradicción, porque significa que los n vectores 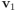 ,
, …
…  no son linealmente independientes.
no son linealmente independientes.
Por lo tanto, dado un vector sólo puede haber una combinación lineal única de los vectores de una base que lo produzca. Los correspondientes coeficientes de la combinación lineal, los números reales  ,
,  …
… 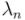 son las componentes del vector
son las componentes del vector  en la base adoptada.
en la base adoptada.
Todas las diferentes bases de un mismo espacio vectorial tienen el mismo número n de vectores, que no es más que la dimensión del espacio vectorial.
Siguiendo con el ejemplo, los vectores  y
y  de la figura de arriba, al ser linealmente independientes, forman una base de un espacio vectorial de dos dimensiones.
de la figura de arriba, al ser linealmente independientes, forman una base de un espacio vectorial de dos dimensiones.
Base ortogonal
Es aquella base de vectores en que cada uno de los vectores que la forman es ortogonal (perpendicular) a todos los demás de la base. Es decir, si  ,
,  …
…  forman una base ortogonal se cumplirá:
forman una base ortogonal se cumplirá:

o lo que es lo mismo:

A partir de una base no ortogonal se puede obtener siempre una base ortogonal. La idea del procedimiento es que a un vector 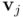 de la base no ortogonal de partida se le puede restar su proyección respecto a otro vector de la base
de la base no ortogonal de partida se le puede restar su proyección respecto a otro vector de la base  y el vector resultante, que siempre será diferente de
y el vector resultante, que siempre será diferente de  y que denominaremos
y que denominaremos  , será ortogonal a
, será ortogonal a  y podrá sustituir a
y podrá sustituir a 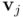 en la base original. Esa es la clave del conocido procedimiento de ortogonalización de Gram-Schmidt, que veremos en detalle en una entrada próxima.
en la base original. Esa es la clave del conocido procedimiento de ortogonalización de Gram-Schmidt, que veremos en detalle en una entrada próxima.
Base ortonormal
Es aquella base ortogonal en que los vectores están normalizados, es decir, tienen norma unidad. Para obtener una base ortonormal a partir de una base ortogonal, basta dividir cada vector de la base original por su norma. Los vectores  ,
,  …
…  de una base ortonormal de un espacio vectorial de n dimensiones cumplen:
de una base ortonormal de un espacio vectorial de n dimensiones cumplen:
 , cuando
, cuando 
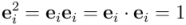 [2]
[2]

Una base ortonormal de  . Los vectores
. Los vectores  ,
,  y
y  que la forman son mutuamente ortogonales y tienen norma unidad.
que la forman son mutuamente ortogonales y tienen norma unidad.
Generación de la base de bivectores
Una vez tenemos la expresión de los vectores del espacio de un espacio n dimensional  en función de una base ortonormal, podemos hacer fácilmente cálculos en el álgebra geométrica asociada
en función de una base ortonormal, podemos hacer fácilmente cálculos en el álgebra geométrica asociada  , una vez expresamos los multivectores en términos de los vectores de esta base.
, una vez expresamos los multivectores en términos de los vectores de esta base.
Recordemos que podemos generar cualquier elemento del álgebra geométrica a partir de los vectores, haciendo productos geométricos y sumas. Partamos, pues, de nuestra base ortonormal de vectores,  ,
,  …
…  , y comencemos por generar todos los posibles productos geométricos de dos vectores de la base ortonormal:
, y comencemos por generar todos los posibles productos geométricos de dos vectores de la base ortonormal:
1) Los productos geométricos de un vector  por sí mismo darán escalares, como ya sabemos, a consecuencia de la ley de contracción (axioma 5 del álgebra geométrica). Como, además, cada
por sí mismo darán escalares, como ya sabemos, a consecuencia de la ley de contracción (axioma 5 del álgebra geométrica). Como, además, cada  está normalizado, cada cuadrado de
está normalizado, cada cuadrado de  será igual a
será igual a  .
.
2) Los productos geométricos de dos vectores diferentes de la base ortonormal generarán una base de bivectores unitarios, a partir de la cual, a su vez, podremos generar mediante combinación lineal cualquier bivector. Efectivamente, tenemos que, para  :
:
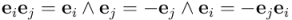
Por tanto podemos formar una base de bivectores, si partimos de una base de n vectores, con los productos geométricos de parejas de vectores diferentes de la base ortonormal de vectores. Como al cambiar el orden del producto de dos vectores se obtiene el mismo bivector, sólo que cambiado de signo, basta con tomar las combinaciones sin repetición de parejas de vectores de la base ortonormal. Para ello, basta tomar las parejas de vectores diferentes de la base ortonormal ordenadas por subíndices crecientes. En dos dimensiones, como sólo tenemos dos vectores en la base ortonormal,  y
y  , la base de bivectores que podremos formar con ellos sólo podrá tener un elemento,
, la base de bivectores que podremos formar con ellos sólo podrá tener un elemento,  . Eso quiere decir que los bivectores de
. Eso quiere decir que los bivectores de  sólo tienen una componente, como los escalares. De hecho, los bivectores son los pseudoescalares de
sólo tienen una componente, como los escalares. De hecho, los bivectores son los pseudoescalares de  . En
. En  , el álgebra geométrica del espacio de dos dimensiones, ya no existen multivectores de grado superior (los trivectores ya representan volúmenes y necesitan por lo menos tres dimensiones).
, el álgebra geométrica del espacio de dos dimensiones, ya no existen multivectores de grado superior (los trivectores ya representan volúmenes y necesitan por lo menos tres dimensiones).

El bivector  (
( ) es la base canónica de los bivectores de
) es la base canónica de los bivectores de  . Como sólo se puede hacer una pareja de vectores ortogonales con los vectores de la base ortonormal de vectores (
. Como sólo se puede hacer una pareja de vectores ortogonales con los vectores de la base ortonormal de vectores ( y
y  ), el bivector
), el bivector  es por sí solo una base de bivectores de
es por sí solo una base de bivectores de  . Cambiando el orden del producto se obtendría
. Cambiando el orden del producto se obtendría  , que no es más que
, que no es más que  . Todos los bivectores (superficies orientadas) de
. Todos los bivectores (superficies orientadas) de  son el producto de un número real por
son el producto de un número real por  , es decir, tienen una única componente real en términos de la base. Por ello, los bivectores son los pseudoescalares de
, es decir, tienen una única componente real en términos de la base. Por ello, los bivectores son los pseudoescalares de  .
.
Si pasamos a tres dimensiones, partiremos de una base ortogonal de tres vectores:  ,
,  y
y  . Con ellos podemos formar tres combinaciones de dos en dos sin repetición.
. Con ellos podemos formar tres combinaciones de dos en dos sin repetición.
Podríamos escoger sin ningún problema como base de bivectores la formada por los productos geométricos donde los índices aparecen ordenados de menor a mayor, es decir:
 ,
,  y
y 
Pero también podemos escoger esta otra base, aparte de otras, que es casi la misma, con la excepción de que se ha cambiado  por
por 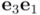 , además de un cambio de orden:
, además de un cambio de orden:
 ,
, 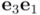 y
y 
Esta base tiene la particularidad, como veremos, de ser la base de bivectores cuyos respectivos duales[3] son los vectores  ,
,  y
y  de la base ortonormal de vectores y frecuentemente es la que se prefiere a la anterior, aunque se trate de una preferencia fundamentalmente estética. En el ejemplo que tenéis al final de la entrada podéis ver por qué.
de la base ortonormal de vectores y frecuentemente es la que se prefiere a la anterior, aunque se trate de una preferencia fundamentalmente estética. En el ejemplo que tenéis al final de la entrada podéis ver por qué.

A la izquierda de la figura, la base de bivectores de  formada por los bivectores
formada por los bivectores  ,
,  y
y  .
.
A la derecha, otra base de bivectores de  , en la que simplemente se ha cambiado el bivector
, en la que simplemente se ha cambiado el bivector  , representado por la superficie orientada de color azul claro, por el bivector
, representado por la superficie orientada de color azul claro, por el bivector 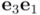 , el bivector con orientación opuesta, representado en por la superficie orientada de color verde claro.
, el bivector con orientación opuesta, representado en por la superficie orientada de color verde claro.
Como la base de los bivectores de  tiene 3 elementos, los bivectores de
tiene 3 elementos, los bivectores de  forman un subespacio lineal de 3 dimensiones, al igual que los vectores de
forman un subespacio lineal de 3 dimensiones, al igual que los vectores de  .
.
En general, cuando partimos de un espacio  de n dimensiones, el número de bivectores de la base serán las combinaciones sin repetición de n elementos tomados de 2 en 2:
de n dimensiones, el número de bivectores de la base serán las combinaciones sin repetición de n elementos tomados de 2 en 2:

Recordemos que la expresión  , que se lee n sobre dos, da el número de combinaciones sin repetición de n tomados de dos en dos. El signo de admiración indica el factorial del número que lo precede. El factorial de un número natural m se puede definir por recurrencia:
, que se lee n sobre dos, da el número de combinaciones sin repetición de n tomados de dos en dos. El signo de admiración indica el factorial del número que lo precede. El factorial de un número natural m se puede definir por recurrencia:
Definimos el factorial de  como:
como:

Definimos el factorial de  en función del factorial de
en función del factorial de  de esta manera:
de esta manera:

Así pues:



y en general:

Por consistencia, se considera también que  .
.
En fin, si en 2 dimensiones el número de bivectores que forman la base es 1, y en 3 dimensiones, la base de bivectores tiene 3 bivectores, en 4 dimensiones, la base de bivectores de  tendrá
tendrá  bivectores.
bivectores.
Generación de las bases de trivectores
Si la dimensión n de  es 3 o superior, habrá que considerar las diferentes combinaciones de productos geométricos de tres vectores diferentes de la base ortonormal de vectores, que nos darán una base de trivectores.
es 3 o superior, habrá que considerar las diferentes combinaciones de productos geométricos de tres vectores diferentes de la base ortonormal de vectores, que nos darán una base de trivectores.
Si consideráramos productos de tres vectores de la base ortonormal con al menos algún vector repetido, lo que obtendríamos serían vectores, como es fácil ver. Ahí va un ejemplo:

Donde hemos aplicado la propiedad de la anticonmutatividad del producto geométrico de los vectores ortogonales, la propiedad de asociatividad del producto geométrico y la ley de contracción del producto geométrico de un vector por sí mismo, vector que ya sabemos normalizado.
En el caso del álgebra  , asociada al espacio tridimensional, como la base de vectores está formada por
, asociada al espacio tridimensional, como la base de vectores está formada por  ,
,  y
y
 , la única forma posible[4]
de obtener un trivector es multiplicar los tres vectores de que se dispone en la base:
, la única forma posible[4]
de obtener un trivector es multiplicar los tres vectores de que se dispone en la base: 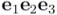 , (que es exactamente lo mismo que
, (que es exactamente lo mismo que  , al ser el producto de tres vectores todos ortogonales entre sí) y representa el volumen orientado del paralelepípedo que tiene por aristas
, al ser el producto de tres vectores todos ortogonales entre sí) y representa el volumen orientado del paralelepípedo que tiene por aristas  ,
,  y
y  , por este orden. Un cambio de orden en el producto representa como mucho un cambio de signo en el resultado final, por ejemplo:
, por este orden. Un cambio de orden en el producto representa como mucho un cambio de signo en el resultado final, por ejemplo:

Es fácil comprobar que los productos de una permutación de tipo par de los vectores en el orden original, es decir, una permutación que se haga a partir de un número par de transposiciones (a cada una de las cuales va asociada un cambio de signo) tienen el mismo signo que 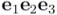 , y los productos de una permutación impar de los vectores tienen el signo cambiado.
, y los productos de una permutación impar de los vectores tienen el signo cambiado.
Por ejemplo, se puede ver que  porque hacen falta dos transposiciones (y un número par de cambios de signo), para transformar un producto en otro. Primero intercambio los dos primeros factores:
porque hacen falta dos transposiciones (y un número par de cambios de signo), para transformar un producto en otro. Primero intercambio los dos primeros factores:

y a continuación los dos últimos factores:

quedando:

De forma parecida procederíamos para en los demás casos.
Como los trivectores de  tienen una única componente, son los pseudoescalares de
tienen una única componente, son los pseudoescalares de  .
.

En la figura se representa el trivector 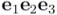 como el volumen orientado del cubo determinado, por los vectores
como el volumen orientado del cubo determinado, por los vectores  ,
,  y
y  , en este orden. La línea quebrada verde, que resigue la dirección de los vectores del producto, indica el sentido del trivector. Si intercambiamos dos vectores cualesquiera en el producto, el trivector resultante cambia de signo.
, en este orden. La línea quebrada verde, que resigue la dirección de los vectores del producto, indica el sentido del trivector. Si intercambiamos dos vectores cualesquiera en el producto, el trivector resultante cambia de signo.
El álgebra geométrica como álgebra graduada
Tal como estamos viendo, los elementos de una álgebra geométrica asociada a un espacio vectorial de n dimensiones se pueden ver como suma formal de diferentes términos, comenzando por una parte escalar, de grado 0, que tendrá una única componente, una parte vectorial, de grado 1, que tendrá n componentes, una parte bivectorial, de grado 2, que tendrá  componentes… y así hasta llegar a una parte n-vectorial con sólo una componente (ya que
componentes… y así hasta llegar a una parte n-vectorial con sólo una componente (ya que  ).
).
Caso n = 2
En un multivector genérico  del álgebra geométrica asociada al espacio bidimensional,
del álgebra geométrica asociada al espacio bidimensional,  , podremos distinguir tres partes: una escalar (real), una vectorial y una bivectorial:
, podremos distinguir tres partes: una escalar (real), una vectorial y una bivectorial:

1) La parte escalar, de grado 0, es un número real  .
.

La notación  indica que nos quedamos con la parte de grado m del multivector
indica que nos quedamos con la parte de grado m del multivector  . En el caso m = 0, lo más habitual es no indicar la m y ya se sobreentiende que vale 0:
. En el caso m = 0, lo más habitual es no indicar la m y ya se sobreentiende que vale 0:  es la parte de grado 0, o parte escalar, de
es la parte de grado 0, o parte escalar, de  .
.
2) La parte vectorial  , de grado 1, consta de dos componentes
, de grado 1, consta de dos componentes  ,
,  que multiplican a los respectivos vectores de la base ortonormal:
que multiplican a los respectivos vectores de la base ortonormal:
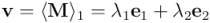
En este caso,  indica la parte de grado 1, o parte vectorial, de
indica la parte de grado 1, o parte vectorial, de  .
.
Por tanto, la parte vectorial vendrá descrita por dos componentes en función de los elementos de la base de vectores.
3) La parte bivectorial  , de grado 2, que resultará de multiplicar un escalar por el bivector
, de grado 2, que resultará de multiplicar un escalar por el bivector  :
:

Por tanto tenemos una única componente bivectorial.  indica la parte de grado 2, o parte bivectorial, de
indica la parte de grado 2, o parte bivectorial, de  .
.
Considerando el álgebra  como espacio lineal,[5] vemos que tiene cuatro dimensiones, al poderse describir sus elementos con cuatro componentes reales:
como espacio lineal,[5] vemos que tiene cuatro dimensiones, al poderse describir sus elementos con cuatro componentes reales:  ,
,  ,
,  y
y  .
.
El álgebra geométrica  , como todas las álgebras geométricas, es una álgebra graduada: en ella hay elementos de grado 0, los escalares (números reales); elementos de grado 1, los vectores (segmentos orientados); y elementos de grado 2, los bivectores (superficies orientadas). Cualquier multivector de
, como todas las álgebras geométricas, es una álgebra graduada: en ella hay elementos de grado 0, los escalares (números reales); elementos de grado 1, los vectores (segmentos orientados); y elementos de grado 2, los bivectores (superficies orientadas). Cualquier multivector de  es una suma formal de estos tres tipos de elementos.
es una suma formal de estos tres tipos de elementos.
Caso n = 3
Un multivector genérico de  tendrá un total de 8 componentes: una componente escalar, tres componentes vectoriales, otras tres componentes bivectoriales y, finalmente, una componente trivectorial:
tendrá un total de 8 componentes: una componente escalar, tres componentes vectoriales, otras tres componentes bivectoriales y, finalmente, una componente trivectorial:

La parte de grado 0, o parte escalar de  , es:
, es:

La parte de grado 1, o parte vectorial de  , es:
, es:

La parte de grado 2, o parte bivectorial de  , es:
, es:

Los bivectores de  tienen tres componentes, como los vectores. En
tienen tres componentes, como los vectores. En  se puede establecer una correspondencia 1 a 1 entre vectores y bivectores.[6] Podemos referirnos a los bivectores de
se puede establecer una correspondencia 1 a 1 entre vectores y bivectores.[6] Podemos referirnos a los bivectores de  como los pseudovectores de
como los pseudovectores de  .
.
Finalmente, la parte de grado 3, la parte trivectorial de  , es:
, es:

Los trivectores de  tienen una sola componente y son los pseudoescalares de
tienen una sola componente y son los pseudoescalares de  . Siempre sucede que los n-vectores de
. Siempre sucede que los n-vectores de  tienen una única componente, como los escalares, y por tanto, son los pseudoescalares de
tienen una única componente, como los escalares, y por tanto, son los pseudoescalares de  .
.

El triángulo de Tartaglia, o también triángulo de Pascal, representa en la posición m de la fila n el coeficiente binomial  , que es el número de m-vectores que forman la base de m-vectores de
, que es el número de m-vectores que forman la base de m-vectores de  . Por las propiedades de los coeficientes binomiales, cada coeficiente binomial puede obtenerse como suma de los dos coeficientes en posiciones más cercanas de la fila superior. En total, si se suman todos los coeficientes binomiales de una cierta fila n, se obtiene
. Por las propiedades de los coeficientes binomiales, cada coeficiente binomial puede obtenerse como suma de los dos coeficientes en posiciones más cercanas de la fila superior. En total, si se suman todos los coeficientes binomiales de una cierta fila n, se obtiene  , que es la dimensión total del álgebra
, que es la dimensión total del álgebra  considerada como espacio lineal.
considerada como espacio lineal.
La figura muestra como sigue el proceso en dimensiones superiores. Por ejemplo, para n = 4, tendremos una componente escalar, 4 componentes vectoriales, 6 componentes bivectoriales, 4 componentes trivectoriales y una componente cuadrivectorial. Se puede apreciar la simetría de los coeficientes binomiales respecto al eje vertical del triángulo de Tartaglia.[7] Para cualquier valor de n, siempre tendremos una sola componente escalar y también una sola componente n-vectorial o pseudoescalar. También tendremos n componentes vectoriales, tantas como componentes (n – 1)-vectoriales,[8] y tantas componentes bivectoriales como (n – 2)-vectoriales, etc. Finalmente, la dimensión total del álgebra geométrica  , considerada como espacio lineal, es la suma de los números del triángulo de Tartaglia para la fila de la n correspondiente: 2 para n = 1, 4 para n = 2, 8 para n = 3, 16 para n = 4, 32 para n = 5, y en el caso general,
, considerada como espacio lineal, es la suma de los números del triángulo de Tartaglia para la fila de la n correspondiente: 2 para n = 1, 4 para n = 2, 8 para n = 3, 16 para n = 4, 32 para n = 5, y en el caso general,  .[9]
.[9]
Ejemplo práctico de cálculo de un producto geométrico
Para acabar esta entrada, veamos cómo se hace en la práctica un producto geométrico de vectores expresados en función de una base ortonormal. No es difícil, lo que hay que saber básicamente es que el producto de un vector unitario por sí mismo es igual a 1 y que el producto de dos vectores ortogonales anticonmuta.[10]
Por ejemplo, supongamos que partimos del espacio vectorial euclídeo de 3 dimensiones,  , en el que tenemos una base ortonormal formada por unos vectores
, en el que tenemos una base ortonormal formada por unos vectores  ,
,  y
y  y tenemos los vectores
y tenemos los vectores  y
y  .
.
Calculemos el producto geométrico  :
:
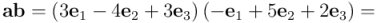
Desarrollemos el producto según la propiedad distributiva:

Aplicamos el axioma 3, según el cual los escalares conmutan con los vectores, y así hacemos los productos de los coeficientes:

Recordemos ahora cómo el producto geométrico de un vector por sí mismo es igual al cuadrado de su norma (la ley de contracción). Como los vectores de la base están normalizados, tendremos que  , sea cual sea el valor del subíndice i. Por otro lado, en los productos cruzados, donde los subíndices son diferentes, aplicaremos la expresión fundamental de descomposición del producto geométrico de vectores en suma de producto escalar y producto vectorial. Pero como dos vectores diferentes de la base son ortonormales tendremos que
, sea cual sea el valor del subíndice i. Por otro lado, en los productos cruzados, donde los subíndices son diferentes, aplicaremos la expresión fundamental de descomposición del producto geométrico de vectores en suma de producto escalar y producto vectorial. Pero como dos vectores diferentes de la base son ortonormales tendremos que  . Es decir, el producto geométrico de dos vectores diferentes de una base ortonormal coincide con el producto exterior, y por tanto anticonmutan, por lo que tendremos que
. Es decir, el producto geométrico de dos vectores diferentes de una base ortonormal coincide con el producto exterior, y por tanto anticonmutan, por lo que tendremos que  , cuando
, cuando  . Por tanto, tendremos:
. Por tanto, tendremos:

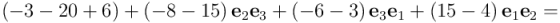

Y nos queda, como esperábamos, la suma formal de un escalar y de un bivector. El escalar es, naturalmente el producto interior  , y el bivector es
, y el bivector es  :
:


Como habéis podido ver, he preferido la ordenación 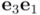 a
a  , ya que es más sugerente a la hora de comparar el producto exterior con el producto vectorial de Heaviside-Gibbs, que sería este:
, ya que es más sugerente a la hora de comparar el producto exterior con el producto vectorial de Heaviside-Gibbs, que sería este:

El producto vectorial de Heaviside-Gibbs da como resultado un vector, que será, como veremos, el vector dual del producto exterior en  . En dimensiones diferentes de n = 3, el dual de un bivector ya no es un vector, y no podemos definir un producto vectorial haciendo el dual de un producto exterior de vectores.
. En dimensiones diferentes de n = 3, el dual de un bivector ya no es un vector, y no podemos definir un producto vectorial haciendo el dual de un producto exterior de vectores.
-
Podríamos utilizar esta expresión y sumarla, previamente multiplicada por un factor real cualquiera, a una expresión del vector
 como combinación lineal de los vectores
como combinación lineal de los vectores 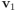 ,
,  y
y  , y obtener infinitas combinaciones lineales, dependiendo del factor que utilicemos, de los tres vectores que producen el vector
, y obtener infinitas combinaciones lineales, dependiendo del factor que utilicemos, de los tres vectores que producen el vector  . Si existen dos combinaciones lineales diferentes que producen un mismo vector, hay infinitas. [↩]
. Si existen dos combinaciones lineales diferentes que producen un mismo vector, hay infinitas. [↩] -
Los matemáticos han inventado una forma compacta, que imagino que muchos conoceréis, para escribir las dos expresiones a la vez:

Donde el símbolo
 , conocido como delta de Kronecker, vale
, conocido como delta de Kronecker, vale 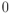 cuando
cuando  y
y  cuando
cuando 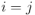 . [↩]
. [↩] -
Ya defineremos en otra entrada en qué consiste la dualidad. [↩]
-
El número de combinaciones sin repetición de n elementos, tomados de 3 en 3 es:

Eso quiere decir que en el caso en que n es igual a 3 la base de trivectores tendrá un único elemento, ya que
 . [↩]
. [↩] -
Espacio lineal es lo mismo que espacio vectorial, pero en álgebra geométrica se prefiere decir espacio lineal, ya que se restringe el concepto de vector al aspecto estrictamente geométrico (“flecha” o “segmento orientado”). [↩]
-
Mediante un mecanismo llamado dualidad, que pronto veremos. [↩]
-
La simetria del triángulo de Tartaglia viene impuesta porque siempre tendremos
 , que expresa el hecho de que el número de formas de elegir m elementos diferentes entre n elementos dados es el mismo número de formas de elegir los n – m elementos que se quieren rechazar. [↩]
, que expresa el hecho de que el número de formas de elegir m elementos diferentes entre n elementos dados es el mismo número de formas de elegir los n – m elementos que se quieren rechazar. [↩] -
Por ello a los (n – 1)-vectores del álgebra
 los podemos llamar pseudovectores. [↩]
los podemos llamar pseudovectores. [↩] -
Una manera de obtener el valor
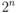 es aplicar la fórmula del teorema del binomio al cálculo de
es aplicar la fórmula del teorema del binomio al cálculo de  :
:
… que, efectivamente, no es más que la suma de los coeficientes de la fila n del triángulo de Tartaglia:
 [↩]
[↩] -
Esto se puede escribir en forma compacta utilizando otra vez la delta de Kronecker, de la que hablábamos anteriormente:

Cuando
 la fórmula equivale a la ley de contracción, y cuando
la fórmula equivale a la ley de contracción, y cuando  equivale a la ley de anticonmutatividad del producto geométrico de vectores ortogonales, como no cuesta comprobar. A veces se ve en algún texto esta fórmula como definición rápida del concepto álgebra de Clifford, para el caso de métrica euclídea. [↩]
equivale a la ley de anticonmutatividad del producto geométrico de vectores ortogonales, como no cuesta comprobar. A veces se ve en algún texto esta fórmula como definición rápida del concepto álgebra de Clifford, para el caso de métrica euclídea. [↩]

The Explorando el álgebra geométrica 10 – Bases ortonormales de vectores, base canónica del álgebra by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.




{ 2 } Comentarios
“Para obtener una base ortonormal a partir de una base ortonormal, … ” (?)
Hola Txarli, …a partir de una base ortogonal, naturalmente. Gracias por la corrección.
Escribe un comentario