Continúo dedicando esta entrada a los números complejos, todavía dentro de la parte de introducción de la serie dedicada al álgebra geométrica. Si en la anterior entrada habíamos tratado los números complejos desde un punto de vista puramente aritmético, ahora veremos cómo los números complejos se representan como puntos en un plano y cómo se visualiza en el plano complejo la suma y el producto de complejos. El producto de complejos será especialmente importante, ya que los rotores (los operadores de rotación) del álgebra geométrica del plano  se pueden identificar con complejos de módulo
se pueden identificar con complejos de módulo  .
.
Representación de los complejos en un plano
Los números complejos no dejaron de ser para los matemáticos esos misteriosos “números imposibles” hasta que se dio con una representación geométrica para ellos. Hubo quien se quedó muy cerca, como John Wallis (1616-1703),[1] pero el primero que lo consiguió fue el danés Caspar Wessel (1745-1818). Wessel fue el primero que identificó un número complejo con un punto en el plano, de modo que la parte real y la parte imaginaria del número complejo, respectivamente, se identifican con las coordenadas cartesianas del punto. También se considera a Wessel el primero que sumó dos vectores. Wessel era cartógrafo, pero al ser como matemático un no profesional, y como además su trabajo de 1797 sobre números complejos solamente fue publicado en danés por la Academia de Ciencias Danesa en 1797, no consiguió despertar el interés de la comunidad matemática internacional. Una lástima, porque en su trabajo ya incluía aplicaciones a la trigonometría, a la geometría plana y esférica e incluso se anunciaban los números hipercomplejos. Hubo que esperar a 1895 para que su figura fuera redescubierta y su prioridad en el descubrimiento reivindicada.
El siguiente en redescubrir la representación en el plano de los números complejos fue otro matemático aficionado, Jean-Robert Argand (1768-1822), un librero ginebrino establecido en París. En 1806 publicó en francés por su cuenta su Ensayo sobre una forma de representar las cantidades imaginarias mediante construcciones geométricas, un libro en que ni siquiera aparece su nombre y que tenía todos los números para caer en el olvido. No obstante, Argand hizo llegar un ejemplar a Adrien-Marie Legendre (1752-1833), quien a su vez lo envió a François Français (1768-1810) para que lo estudiara. Tras la muerte de Français su hermano, Jacques Fréderic, descubre el libro y finalmente lo hizo publicar (1813) en una revista matemática, introduciendo algún añadido personal y dejando claro que la idea no era suya, y que buscaba al autor original. Argand respondió en el siguiente número de la misma revista, y el año siguiente, 1814, publicó la primera demostración rigurosa del teorema fundamental del álgebra, su otra gran contribución a las Matemáticas. Argand es el primero en introducir el concepto de módulo de un número complejo. Por lo demás, en su libro no hay aplicaciones a la geometría, como sí era en el caso del de Wessel.

Carl Friedrich Gauß (Wikimedia, dominio público)
Aún así, los matemáticos todavía siguieron considerando los números complejos como un artificio de cálculo e hizo falta que un matemático de prestigio, pero prestigio de verdad, nada menos que Carl Friedrich Gauß [2] (1777-1855), el príncipe de los matemáticos, para convencer a la comunidad matemática de que los números complejos abrían las puertas a fascinantes resultados. Gauß introduce la interpretación geométrica de los números complejos en una memoria de 1831, pero allí hace la observación de que ya había usado la idea en su tesis doctoral de 1799.[3]
La idea que inspiró a Wessel, Argand y Gauß viene a ser esta: si representamos los números reales en una recta, ordenados crecientemente, con los números positivos a la derecha del  y los negativos a su izquierda, multiplicar por
y los negativos a su izquierda, multiplicar por  un número real es aplicarle un giro de
un número real es aplicarle un giro de  alrededor del
alrededor del  . Para multiplicar
. Para multiplicar  por
por  en la recta real, giro
en la recta real, giro  en torno al
en torno al  y voy a parar al
y voy a parar al  . Si vuelvo a multiplicar
. Si vuelvo a multiplicar  por
por  , doy otra vuelta de
, doy otra vuelta de  y vuelvo a
y vuelvo a  . Multiplicar dos veces seguidas por
. Multiplicar dos veces seguidas por  es lo mismo que multiplicar por
es lo mismo que multiplicar por  , y gráficamente corresponde a dar dos medias vueltas de
, y gráficamente corresponde a dar dos medias vueltas de  , o sea,
, o sea,  . Pues bien, ¿qué puede significar entonces multiplicar por
. Pues bien, ¿qué puede significar entonces multiplicar por  ?
?
Pues bien, como  , multiplicar dos veces por
, multiplicar dos veces por  es aplicar un giro de
es aplicar un giro de  . Entonces, multiplicar una vez por
. Entonces, multiplicar una vez por  tendrá que ser… aplicar un giro de
tendrá que ser… aplicar un giro de  . Y de esta forma, al multiplicar los números reales por
. Y de esta forma, al multiplicar los números reales por  , la recta real se transforma en un eje perpendicular de números imaginarios:
, la recta real se transforma en un eje perpendicular de números imaginarios:
Y ya está: multiplicar por  hace girar la semirrecta de los reales positivos
hace girar la semirrecta de los reales positivos  , multiplicar por
, multiplicar por  la hace girar la semirrecta
la hace girar la semirrecta  , convirtiendo cada número real
, convirtiendo cada número real 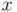 en su opuesto,
en su opuesto,  , multiplicar por
, multiplicar por  hará girar la semirrecta
hará girar la semirrecta  , multiplicar por
, multiplicar por  deja la semirrecta de los reales positivos igual (sería girar
deja la semirrecta de los reales positivos igual (sería girar  ). Es decir:
). Es decir:
Las sucesivas potencias enteras de la unidad imaginaria  van girando por cuartos de vuelta en el plano complejo a medida que el exponente se va incrementando en una unidad:
van girando por cuartos de vuelta en el plano complejo a medida que el exponente se va incrementando en una unidad:






Los complejos se pueden representar geométricamente en un plano (llamado plano de Argand, y a veces también plano de Gauß, aunque ahora sepamos que deberíamos llamarlo plano de Wessel ) definiendo en él un sistema de coordenadas cartesianas, y asignando a cada complejo un punto del plano cuya primera componente sea la parte real de  y la segunda su parte imaginaria.
y la segunda su parte imaginaria.
La suma de complejos se puede visualizar en el plano de Argand igual que una suma de vectores. A un número complejo  representado en un punto del plano le podemos asignar igualmente el vector que parte del punto asociado al número complejo
representado en un punto del plano le podemos asignar igualmente el vector que parte del punto asociado al número complejo  (donde se cortan los ejes real e imaginario) hasta el punto donde se sitúa el propio
(donde se cortan los ejes real e imaginario) hasta el punto donde se sitúa el propio  . El resultado de la suma de dos complejos
. El resultado de la suma de dos complejos  y
y  se corresponde con la suma de los respectivos vectores que los identifican. Si necesitas una explicación de cómo se suman vectores, Pedro explica el concepto de vector y dedica un apartado a explicar la suma y resta de vectores en esta entrada de su bloque de Matemáticas I.
se corresponde con la suma de los respectivos vectores que los identifican. Si necesitas una explicación de cómo se suman vectores, Pedro explica el concepto de vector y dedica un apartado a explicar la suma y resta de vectores en esta entrada de su bloque de Matemáticas I.
La representación de los complejos en un plano permite pensar en utilizar un sistema de coordenadas polares, en que cada complejo se representa, en vez de por sus componentes cartesianas (que serían  y
y  ) , mediante su distancia al origen
) , mediante su distancia al origen  y el ángulo
y el ángulo  que forma el segmento que lo une al origen con el eje de abscisas (o eje real). El número real
que forma el segmento que lo une al origen con el eje de abscisas (o eje real). El número real  que expresa la distancia al origen es el módulo del número complejo
que expresa la distancia al origen es el módulo del número complejo  (usaremos la notación
(usaremos la notación  para referirnos al módulo de un complejo
para referirnos al módulo de un complejo  ), y lo podemos calcular aplicando el teorema de Pitágoras al triángulo rectángulo de catetos a y b y de hipotenusa
), y lo podemos calcular aplicando el teorema de Pitágoras al triángulo rectángulo de catetos a y b y de hipotenusa  :
:

Pero por otra parte, teníamos que:

Así pues, resulta que  , y el módulo
, y el módulo  que buscamos será:
que buscamos será:

El ángulo  es el argumento del complejo
es el argumento del complejo  . La tangente del argumento es, como se deduce de la figura siguiente, el cociente
. La tangente del argumento es, como se deduce de la figura siguiente, el cociente  :
:

O de modo equivalente:

Recurriendo a la trigonometría tenemos lo siguiente:
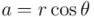

Y por tanto, podemos reescribir  como:
como:
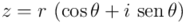
De este modo, el número complejo  queda expresado como producto de un número real (su módulo
queda expresado como producto de un número real (su módulo  ) por un número complejo unitario
) por un número complejo unitario  . Se llama unitario porque su módulo vale
. Se llama unitario porque su módulo vale  . Para convencerse de ello sólo hace falta aplicar una conocida fórmula de trigonometría elemental:
. Para convencerse de ello sólo hace falta aplicar una conocida fórmula de trigonometría elemental:

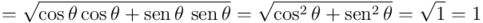
Y todavía podemos reescribir  como producto de su módulo por la exponencial de
como producto de su módulo por la exponencial de  veces su argumento:
veces su argumento:

Para ello, se ha utilizado la famosísima fórmula de Euler:

He decidido finalmente no caer en la tentación de hacer la deducción aquí, aunque sea muy bonita, pero al final no he querido recargar más la entrada hablando de desarrollos en serie. Si no sabes cómo se deduce esa fórmula, te recomiendo encarecidamente que visites este enlace.
La fórmula de Euler nos dice que un número complejo unitario de argumento  no es más que
no es más que  . En el caso que
. En el caso que  valga
valga 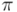 radianes (corresponde a un argumento de
radianes (corresponde a un argumento de  ) obtenemos esta curiosa fórmula, que relaciona los cinco números más importantes de las Matemáticas:
) obtenemos esta curiosa fórmula, que relaciona los cinco números más importantes de las Matemáticas:

Basta ahora pasar el  al otro lado de la igualdad con el signo cambiado:
al otro lado de la igualdad con el signo cambiado:

Ahí están: el  , el
, el  ,
, 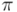 (razón de la longitud de la circunferencia a su diámetro, de valor aproximado
(razón de la longitud de la circunferencia a su diámetro, de valor aproximado  ),
), 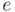 (base de los logaritmos naturales, de valor aproximado
(base de los logaritmos naturales, de valor aproximado  ), y, por fin, la unidad imaginaria
), y, por fin, la unidad imaginaria  .
.
El conjugado de un complejo de módulo  y argumento
y argumento  es simplemente el complejo con el mismo módulo y argumento cambiado de signo:
es simplemente el complejo con el mismo módulo y argumento cambiado de signo:


Como tiene que ser, se cumple:

Producto de dos números complejos dados los módulos y los argumentos
La regla es muy simple, y además es coherente con la idea que nos llevó a representar el conjunto  de los complejos en un plano en que el eje imaginario es perpendicular el eje real (la idea de que multiplicar por
de los complejos en un plano en que el eje imaginario es perpendicular el eje real (la idea de que multiplicar por  es girar
es girar  ). De hecho, es su consecuencia lógica e inevitable:
). De hecho, es su consecuencia lógica e inevitable:
El producto de dos números complejos es un número complejo cuyo módulo es el producto de los módulos de los factores y su argumento es la suma de los argumentos de los factores.
Veámoslo:
Tenemos dos números complejos  y
y  , con respectivos módulos
, con respectivos módulos  y
y  , y respectivos argumentos
, y respectivos argumentos  y
y  :
:


Calculemos su producto, agrupando el producto de módulos (que es un producto de números reales) por un lado y el producto de los paréntesis (los complejos unitarios asociados a los argumentos respectivos) por otro:


Y agrupando, en el interior del paréntesis, las partes real e imaginaria por separado, obtenemos esto:

![+ i{\color{green} (\cos\theta_1\operatorname{sen}\theta_2+\operatorname{sen}\theta_1\cos\theta_2)}]](http://eltamiz.com/elcedazo/wp-content/uploads/2017/08/tex80_9152955cf5d7c57efbbf09128f17737d.png)
Y llegados aquí, reconocemos que la parte real del corchete (el contenido del primer paréntesis, en rojo) es la conocida expresión trigonométrica que da el coseno de la suma de dos ángulos, y la parte imaginaria del corchete (el contenido del segundo paréntesis, en verde) es la expresión del seno de la suma de dos ángulos, y por tanto lo que tenemos al final es esto:
![z_1 z_2 = r_1 r_2 [{\color{red}\cos(\theta_1+\theta_2)} + i{\color{green}\operatorname{sen}(\theta_1+\theta_2)} = r_1 r_2 e^{i \left(\theta_1 + \theta_2\right)}]](http://eltamiz.com/elcedazo/wp-content/uploads/2018/05/tex80_c3edbb871498ec740878c64842cff178.png)
Y efectivamente, hemos expresado el producto de  y
y  nuevamente en forma del producto de un número real, que es
nuevamente en forma del producto de un número real, que es  , por un número complejo unitario que se puede escribir en la forma
, por un número complejo unitario que se puede escribir en la forma  , donde el argumento
, donde el argumento  no es más que la suma de argumentos,
no es más que la suma de argumentos,  .
.
Es cierto que también podríamos habernos ahorrado el uso de trigonometría si hubiéramos usado las expresiones en forma polar, aprovechando que el producto de exponenciales es simplemente la exponencial de la suma de los exponentes:

Ciertamente es mucho más fácil e inmediato así, pero debo advertir que el hecho de que el producto de exponenciales sea igual a la exponencial de la suma es cierto en el caso de los números complejos gracias a que el producto de complejos es conmutativo. Cuando veamos en entradas posteriores el cuerpo asimétrico  de los cuaterniones, cuyo producto no conmuta, normalmente ya no se cumplirá que el producto de exponenciales es igual a la exponencial de la suma.
de los cuaterniones, cuyo producto no conmuta, normalmente ya no se cumplirá que el producto de exponenciales es igual a la exponencial de la suma.
Potencias y raíces de un número complejo en forma polar
Finalmente, la forma polar también permite expresar las potencias y raíces de un número complejo de forma particularmente simple. Para elevar a la potencia 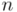 un número complejo
un número complejo  :
:

Es decir, la potencia 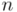 de un número complejo
de un número complejo es un complejo cuyo módulo es la potencia
es un complejo cuyo módulo es la potencia 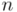 del módulo de
del módulo de  y su argumento es
y su argumento es 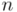 veces el argumento de
veces el argumento de  . Si reexpresamos las exponenciales en función de cosenos y senos:
. Si reexpresamos las exponenciales en función de cosenos y senos:

Y simplificando el factor  llegamos a la célebre fórmula de de Moivre, que da la potencia
llegamos a la célebre fórmula de de Moivre, que da la potencia 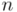 de un complejo unitario:[4]
de un complejo unitario:[4]

Es decir, la potencia 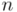 de un complejo unitario es un complejo unitario cuyo argumento es el argumento del complejo original multiplicado por
de un complejo unitario es un complejo unitario cuyo argumento es el argumento del complejo original multiplicado por 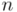 .
.
Por otro lado, para encontrar una raíz 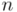 de un complejo
de un complejo  , o sea el complejo que elevado a
, o sea el complejo que elevado a 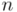 da
da  , basta tomar el complejo cuyo módulo es la raíz
, basta tomar el complejo cuyo módulo es la raíz 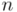 del módulo de
del módulo de  , y cuyo argumento es el argumento de
, y cuyo argumento es el argumento de  dividido por
dividido por 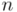 :
:
![\sqrt[n]{z} = z^{\frac{1}{n}} = (r e^{i\theta})^{\frac{1}{n}} = r^{\frac{1}{n}} (e^{i\theta})^{\frac{1}{n}} = \sqrt[n]{r} e^{i\frac{\theta}{n}}](http://eltamiz.com/elcedazo/wp-content/uploads/2017/08/tex80_9fa53ebf332c8856bb99c8c70c95be5d.png)
En este caso hay que tener en cuenta que esta no es la única raíz 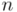 -sima de
-sima de  posible, sino una de
posible, sino una de 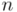 posibles, ya que podemos multiplicarla por un complejo unitario
posibles, ya que podemos multiplicarla por un complejo unitario  , donde
, donde  es un número entero desde
es un número entero desde  a
a  . Esto es así porque
. Esto es así porque  elevado a
elevado a 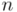 , con
, con  entero da siempre
entero da siempre  (porque
(porque  radianes son
radianes son  vueltas de
vueltas de  ):
):

La fórmula de la raíz 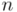 -sima de
-sima de  queda entonces como:
queda entonces como:
![\sqrt[n]{z} = \sqrt[n]{r} e^{i\frac{\theta}{n}+i\frac{2k\pi}{n}}](http://eltamiz.com/elcedazo/wp-content/uploads/2017/08/tex80_26fb7118624149340c44e10afe831d19.png) donde
donde 
Ejemplo: Calcular las raíces cúbicas de  (número complejo de módulo
(número complejo de módulo  y argumento
y argumento  )
)
Como es una raíz cúbica ( ) habrá tres soluciones. Todas ellas tendrán por módulo la raíz cúbica del módulo del número de partida, que será
) habrá tres soluciones. Todas ellas tendrán por módulo la raíz cúbica del módulo del número de partida, que será ![\sqrt[3]{8} = 2](http://eltamiz.com/elcedazo/wp-content/uploads/2017/08/tex80_aae2ac845a729da53b6a3a79cc4458ae.png) . Los argumentos de las sucesivas soluciones estarán espaciados por tercios de vuelta (como una vuelta son
. Los argumentos de las sucesivas soluciones estarán espaciados por tercios de vuelta (como una vuelta son  radianes, un tercio de vuelta son
radianes, un tercio de vuelta son  radianes) y el argumento de la primera solución será la el argumento del complejo de partida dividido por
radianes) y el argumento de la primera solución será la el argumento del complejo de partida dividido por  , o sea
, o sea  (o lo que es lo mismo, un ángulo de
(o lo que es lo mismo, un ángulo de  ). Las tres soluciones serán, por tanto:
). Las tres soluciones serán, por tanto:



Podemos ver que se cumple que el cubo de cada una de ellas da  :
:










Vemos que al elevar al cubo la solución  se introduce un factor
se introduce un factor  , que os he marcado en rojo y que corresponde a una vuelta completa extra, y por tanto
, que os he marcado en rojo y que corresponde a una vuelta completa extra, y por tanto  . Al elevar al cubo la solución
. Al elevar al cubo la solución  , se introduce un factor
, se introduce un factor  , que os he marcado otra vez en rojo y que corresponde a dos vueltas completas, y por tanto resulta nuevamente
, que os he marcado otra vez en rojo y que corresponde a dos vueltas completas, y por tanto resulta nuevamente  .
.
El producto de complejos unitarios como representación de las rotaciones en torno a un punto en el plano bidimensional
De lo que hemos visto deducimos que el producto de dos complejos unitarios es el complejo unitario cuyo argumento es la suma de los argumentos de los dos números complejos de partida:

La representación gráfica de los complejos en el plano de Argand nos permite identificar un complejo unitario de argumento  con una rotación de ángulo
con una rotación de ángulo  , de modo que el producto de complejos unitarios reproduce el comportamiento de la composición de rotaciones en el plano en torno a un punto. En terminología matemática, el conjunto de los complejos unitarios dotado de la operación producto es una representación del grupo de rotaciones en el plano en torno a un punto. Más adelante veremos, ya dentro del contexto del álgebra geométrica
, de modo que el producto de complejos unitarios reproduce el comportamiento de la composición de rotaciones en el plano en torno a un punto. En terminología matemática, el conjunto de los complejos unitarios dotado de la operación producto es una representación del grupo de rotaciones en el plano en torno a un punto. Más adelante veremos, ya dentro del contexto del álgebra geométrica  del plano bidimensional, que podemos considerar a los números complejos unitarios como operadores de rotación, que permiten calcular cómo actúa una rotación sobre los diferentes objetos del álgebra, sean escalares, vectores o bivectores.
del plano bidimensional, que podemos considerar a los números complejos unitarios como operadores de rotación, que permiten calcular cómo actúa una rotación sobre los diferentes objetos del álgebra, sean escalares, vectores o bivectores.
Pero antes de pasar al terreno del álgebra geométrica deberíamos antes ver los cuaterniones, un sistema de números hipercomplejos descubierto por William R. Hamilton en su intento de extender los números complejos a tres dimensiones.
-
Wallis hizo un estudio sobre el cálculo del lado de un triángulo, dado otro lado y el ángulo opuesto al lado buscado, problema que puede tener dos, una o… ninguna solución, caso este último en que el cálculo numérico dé soluciones complejas. Surgía así una interpretación del número complejo como una especie “medida de la imposibilidad” de la solución del problema. [↩]
-
Seguro que estáis más acostumbrados a verlo escrito como Gauss, pero con la generalización del uso de la codificación Unicode en Internet, no veo razón para no escribir Gauß, igual que hacen los alemanes. Si no queréis o no podéis usar el carácter ‘ß’, seguid usando ‘ss’, que es la única alternativa viable. [↩]
-
Gauß era de los que no se obsesionaban por cuestiones de prioridad en sus descubrimientos, que más de una vez reservó para él solo. Es muy conocido que no publicó sus descubrimientos sobre geometrías no euclídeas, y más adelante podremos hablar de otro caso menos conocido, pero relacionado con la temática de esta serie. [↩]
-
La fórmula de de Moivre permite demostrar de forma rápida muchas identidades trigónométricas . Por ejemplo, si queréis encontrar las fórmulas del coseno y del seno del ángulo triple, basta tomar respectivamente la parte real y la parte imaginaria en esta expresión, tras haber desarrollado el cubo del paréntesis final:
 [↩]
[↩]

The Explorando el álgebra geométrica 2 – Antecedentes – Los números complejos (II) by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.










{ 5 } Comentarios
Hola Juan.
Estoy muy interesado en el tema este del algebra geométrica.
Solo aclarar que hay un gazapo en la fórmula del argumento de un número complejo:
$\theta=arctg(b/a)$
Espero ansioso tus siguientes entradas.
Hola adpp, He corregido tres expresiones, para poner b/a en lugar de a/b. Creo que eso era todo. Muchas gracias.
Muy ameno y claro el artículo, gracias por todo el trabajazo que haceis sobre temas tan interesantes.
Primero que todo, gracias por tu esfuerzo en traernos esta nueva serie para disfrutar. Y en segundo lugar quería, si me permiten, recomendar una serie de vídeos de Welch Labs llamada “Imaginary Numbers Are Real”, la cual pueden encontrar en Youtube. Me resultó muy didáctica y puede ayudar a visualizar el concepto de los números complejos. Saludos.
Hola CarlosF, Gracias a ti por tu interés. No conocía esa serie de vídeos, y efectivamente está muy bien. Para los que estamos familiarizados con el álgebra geométrica, el título de esta serie trae a la memoria el de un artículo titulado precisamente al revés: “Imaginary Numbers are not Real: the Geometric Algebra of Spacetime”, de Gull, Lasenby y Doran. Lo que pretendían los autores es enfatizar el enfoque del álgebra geométrica, totalmente “alérgico” al uso de los números complejos (en el sentido de “escalares complejos”) en Física. Al estudiar Física es típico encontrarse por primera vez los números complejos al estudiar la corriente alterna, pero puede considerarse un artificio de cálculo. Cuando realmente hacen los complejos su entrada en la Física “por la puerta grande” es en la mecánica cuántica, donde son imprescindibles (admiro cómo Pedro se atrevió a hacer su serie de cuántica sin mencionar los números complejos). Al hacer mecánica cuántica con álgebra geométrica (tranquilidad, en esta serie sólo haré alguna mención a la mecánica cuántica de pasada) hay que sustituir la unidad imaginaria, i, por algún multivector que tenga cuadrado negativo. Con ello se obliga a dar interpretación geométrica a lo que en mecánica cuántica convencional es un abstracto “escalar imaginario”, cuyo uso está absolutamente proscrito en álgebra geométrica.
Escribe un comentario