En esta nueva entrada de la serie que dedicamos al álgebra geométrica seguiré tratando el tema de las rotaciones en tres dimensiones, y en particular en una diferencia clave al modo en que las rotaciones en tres dimensiones se tratan convencionalmente (con matrices ortogonales de  ). Matemáticamente se expresa diciendo que el grupo de rotores (los cuaterniones unitarios) recubre doblemente al grupo
). Matemáticamente se expresa diciendo que el grupo de rotores (los cuaterniones unitarios) recubre doblemente al grupo  . Veamos en qué consiste eso…
. Veamos en qué consiste eso…
En la pasada entrada ya comenté que una misma rotación  se podía representar por una sola matriz
se podía representar por una sola matriz  de
de  , pero por dos rotores diferentes de
, pero por dos rotores diferentes de  , ya que en la fórmula de rotación de un multivector:
, ya que en la fórmula de rotación de un multivector:

si cambiamos el rotor  por su opuesto,
por su opuesto,  , obtendremos el mismo resultado. Tanto
, obtendremos el mismo resultado. Tanto  como
como  representan la misma rotación.
representan la misma rotación.
Esto podría parecer a primera vista un defecto de los rotores respecto a las matrices como representación de las rotaciones en  , pero investiguemos un poco qué sucede cuando vamos rotando aldrededor de un eje
, pero investiguemos un poco qué sucede cuando vamos rotando aldrededor de un eje  , comenzando por un ángulo de rotación
, comenzando por un ángulo de rotación  nulo y haciéndolo cada vez mayor. Veamos los rotores correspondientes:
nulo y haciéndolo cada vez mayor. Veamos los rotores correspondientes:
Hemos comenzado por una rotación nula, a la se asocia un rotor que resulta valer 1. Efectivamente, si rotamos 0 radianes un multivector  cualquiera obtenemos el mismo multivector:
cualquiera obtenemos el mismo multivector:  . Para rotar un ángulo
. Para rotar un ángulo 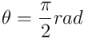 (= 90º) obtenemos también otro valor bien determinado para
(= 90º) obtenemos también otro valor bien determinado para  , así como para los valores de
, así como para los valores de  siguientes:
siguientes: 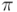 (= 180º),
(= 180º),  (= 270º) y finalmente
(= 270º) y finalmente  (= 360º). Y aquí vemos que el rotor obtenido para
(= 360º). Y aquí vemos que el rotor obtenido para  es
es 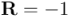 , que no es el mismo obtenido para
, que no es el mismo obtenido para  . Tras dar una vuelta completa, aunque el objeto rotado quede igual, el rotor aplicado es diferente del correspondiente a no hacer ninguna rotación. A una vuelta de 360º le corresponde un rotor
. Tras dar una vuelta completa, aunque el objeto rotado quede igual, el rotor aplicado es diferente del correspondiente a no hacer ninguna rotación. A una vuelta de 360º le corresponde un rotor 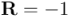 . Pues bien, sigamos rotando en torno al mismo eje
. Pues bien, sigamos rotando en torno al mismo eje  en el mismo sentido hasta completar una segunda vuelta:
en el mismo sentido hasta completar una segunda vuelta:
Y vemos que el rotor  no vuelve a valer 1 hasta que se han dado dos vueltas completas. Para todos estos valores de
no vuelve a valer 1 hasta que se han dado dos vueltas completas. Para todos estos valores de  :
: 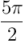 ( = 450º = 360º + 90º ),
( = 450º = 360º + 90º ),  ( = 540º = 360º + 180º ),
( = 540º = 360º + 180º ),  ( = 630º = 360º + 270º ) y
( = 630º = 360º + 270º ) y  ( = 360º + 360º ) vemos que el correspondiente rotor no es más que el rotor asociado a la rotación correspondiente a una vuelta menos, pero cambiado de signo.
( = 360º + 360º ) vemos que el correspondiente rotor no es más que el rotor asociado a la rotación correspondiente a una vuelta menos, pero cambiado de signo.
Ahora podríamos preguntarnos si este extraño comportamiento de los rotores tiene su reflejo en el mundo real. Si rotamos cualquier cosa una vuelta de 360º, aparentemente sigue igual y no ha cambiado nada en absoluto respecto a su estado antes de la rotación. Aparentemente, podríamos pensar que el comportamiento de los rotores no pasa de ser una curiosidad matemática que no tiene aplicación en el mundo físico, y que con las matrices de  , que no exhiben este fenómeno, ya es posible describir perfectamente todo lo asociado a las rotaciones en Física.
, que no exhiben este fenómeno, ya es posible describir perfectamente todo lo asociado a las rotaciones en Física.
Pero resulta que estaríamos muy equivocados. Mi profesor de Mecánica Cuántica, allá en cuarto curso de carrera, lo decía más o menos así: “Si preguntáis a un físico cuál es el grupo de rotaciones del espacio euclídeo tridimensional, es muy probable que os responda que es  , pero un físico que se dedique a la Mecánica Cuántica sabe que el auténtico grupo de rotaciones es
, pero un físico que se dedique a la Mecánica Cuántica sabe que el auténtico grupo de rotaciones es  “.
“.
Bien, ya sabemos que  es el grupo multiplicativo de matrices de números reales organizados en tres filas y tres columnas, matrices que además son ortogonales (de ahí la “O” de
es el grupo multiplicativo de matrices de números reales organizados en tres filas y tres columnas, matrices que además son ortogonales (de ahí la “O” de  ) y de determinante igual a +1 (de ahí la “S” de
) y de determinante igual a +1 (de ahí la “S” de  , que viene de “special”), pero ¿qué es
, que viene de “special”), pero ¿qué es  ? Pues resulta que
? Pues resulta que  es un grupo multiplicativo de matrices, cuyos elementos son números complejos, organizados en dos filas y dos columnas, matrices que además son unitarias[1](de ahí la “U” de
es un grupo multiplicativo de matrices, cuyos elementos son números complejos, organizados en dos filas y dos columnas, matrices que además son unitarias[1](de ahí la “U” de  ) y de determinante igual a +1 (de ahí viene también la “S” de
) y de determinante igual a +1 (de ahí viene también la “S” de  ). En fin, una cosa bastante retorcida y que, efectivamente, es un engendro matemático muy sofisticado para representar el grupo de rotores que actúan sobre cualquier elemento de
). En fin, una cosa bastante retorcida y que, efectivamente, es un engendro matemático muy sofisticado para representar el grupo de rotores que actúan sobre cualquier elemento de  : podemos identificar un rotor
: podemos identificar un rotor  perteneciente al conjunto de todos los rotores de
perteneciente al conjunto de todos los rotores de  con una matriz de
con una matriz de  , y, del mismo modo, podemos identificar una matriz de
, y, del mismo modo, podemos identificar una matriz de  de forma unívoca con un rotor perteneciente al conjunto de todos los rotores de
de forma unívoca con un rotor perteneciente al conjunto de todos los rotores de  , de modo que el producto de dos rotores queda representado por el producto de las correspondientes matrices de
, de modo que el producto de dos rotores queda representado por el producto de las correspondientes matrices de  . El grupo de rotores del álgebra geométrica del espacio euclídeo tridimensional y el grupo
. El grupo de rotores del álgebra geométrica del espacio euclídeo tridimensional y el grupo  son matemáticamente indistinguibles.[2]
son matemáticamente indistinguibles.[2]
Pero entonces, ¿existe algo en el mundo físico que se comporte como un rotor y que necesite dos vueltas para volver a su estado inicial cuando se lo rota? Resulta que en el mundo de la mecánica cuántica tenemos los fermiones, las partículas elementales (como los leptones, entre los que tenemos los electrones, los muones y los tauones; o los quarks) que constituyen la materia ordinaria. Los fermiones se caracterizan por tener espín semientero, a diferencia de los bosones, partículas de espín entero, como pueden ser el fotón, transmisor de la fuerza electromagnética, los bosones W y Z, transmisores de la fuerza débil, o el gravitón, hipotético transmisor de la interacción gravitatoria. Un electrón tiene espín  , y como todas las partículas de espín
, y como todas las partículas de espín  , su función de onda se representa en mecánica cuántica en forma espinorial[3]. En términos del álgebra geométrica, eso quiere decir que para rotar la función de onda de un electrón, que podemos representar por un espinor (en el álgebra geométrica del espacio tridimensional, un cuaternión, recordemos lo dicho en la entrada 13), basta multiplicarlo por delante por el rotor correspondiente (que desde el punto de vista del álgebra geométrica también es un espinor, por ser un cuaternión). Y si queremos rotar la función de onda que describe al electrón una vuelta completa (360º =
, su función de onda se representa en mecánica cuántica en forma espinorial[3]. En términos del álgebra geométrica, eso quiere decir que para rotar la función de onda de un electrón, que podemos representar por un espinor (en el álgebra geométrica del espacio tridimensional, un cuaternión, recordemos lo dicho en la entrada 13), basta multiplicarlo por delante por el rotor correspondiente (que desde el punto de vista del álgebra geométrica también es un espinor, por ser un cuaternión). Y si queremos rotar la función de onda que describe al electrón una vuelta completa (360º =  rad), el rotor correspondiente es
rad), el rotor correspondiente es 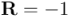 , como vimos antes. Por tanto, la función de onda de un electrón, tras una vuelta completa, cambia de signo, y para tenerla igual que al principio, necesitaríamos aplicar una segunda vuelta completa. Un electrón, por así decirlo, no vuelve a estar como al principio hasta que no ha rotado 720º en torno a un eje.[4]
, como vimos antes. Por tanto, la función de onda de un electrón, tras una vuelta completa, cambia de signo, y para tenerla igual que al principio, necesitaríamos aplicar una segunda vuelta completa. Un electrón, por así decirlo, no vuelve a estar como al principio hasta que no ha rotado 720º en torno a un eje.[4]
Hemos encontrado en el esotérico mundo de la mecánica cuántica un ejemplo de objeto que no vuelve a verse igual hasta que se le ha aplicado una rotación de 720º, pero ¿sería posible encontrar un ejemplo análogo en el mundo cotidiano y macroscópico del mismo comportamiento? La respuesta es SÍ, aunque debemos buscar en los casos de rotaciones de objetos de alguna forma “atados” a su entorno. Por ejemplo, un objeto rotado por un brazo, lo que se conoce como truco del plato o truco del cinturón. Aquí es más bien el “truco del libro”:

Vamos a rotar un libro con un brazo en saltos de 90º hasta que todo quede en la misma posición de partida. En esta primera serie de fotos rotamos el libro hasta 270º.

En la primera foto de esta serie, llegamos a dar una vuelta completa al libro, pero la postura del brazo que lo ha rotado no es exactamente la misma (sobre todo en lo referente a comodidad) que al principio. No importa: seguimos rotando en la misma dirección (esta vez pasando el brazo por encima de la cabeza), que ya se arreglará…
Podemos considerar que la postura del brazo, a lo largo del proceso, va asociada a un determinado rotor  . De hecho en robótica los rotores (como cuaterniones unitarios) han encontrado una importante aplicación para representar de forma eficiente la postura de un brazo robótico, así como para encontrar el modo más efectivo para pasar de una cierta postura a otra.
. De hecho en robótica los rotores (como cuaterniones unitarios) han encontrado una importante aplicación para representar de forma eficiente la postura de un brazo robótico, así como para encontrar el modo más efectivo para pasar de una cierta postura a otra.
Este tipo de modelos también tiene su relevancia en mecánica cuántica: podríamos pensar que un electrón, como cualquier partícula de espín  , es un objeto ligado de algún modo a su entorno por una especie de “brazo invisible”. De hecho, se han utilizado para explicar conceptos relacionados con el espín, o incluso explicar los conceptos que hay detrás de la demostración de teoremas muy complejos de la mecánica cuántica, como el teorema de conexión espín-estadística, por el cual se demuestra que las partículas de espín semientero son fermiones, y por tanto, siguen el principio de exclusión de Pauli, y las partículas de espín entero son bosones, y por tanto, el principio de exclusión no las afecta.[5]
, es un objeto ligado de algún modo a su entorno por una especie de “brazo invisible”. De hecho, se han utilizado para explicar conceptos relacionados con el espín, o incluso explicar los conceptos que hay detrás de la demostración de teoremas muy complejos de la mecánica cuántica, como el teorema de conexión espín-estadística, por el cual se demuestra que las partículas de espín semientero son fermiones, y por tanto, siguen el principio de exclusión de Pauli, y las partículas de espín entero son bosones, y por tanto, el principio de exclusión no las afecta.[5]

Espectacular ilustración del llamado “truco del cinturón” o “truco del plato”, esta vez con un objeto ligado de forma múltiple a su entorno. La configuración no vuelve a ser la inicial hasta que se han dado dos vueltas completas.
http://creativecommons.org/publicdomain/zero/1.0/deed.en
Para la siguiente entrada seguiré con la composición de rotaciones en torno a ejes fijos respecto al sólido rígido que se rota, con lo que acabaría con el tratamiento de las rotaciones en el espacio euclídeo tridimensional.
-
Unitariedad, cuando se habla de matrices, es la propiedad que extiende a matrices de elementos complejos la propiedad de ortogonalidad de las matrices reales: si una matriz ortogonal es aquella cuya inversa es su matriz transpuesta, como vimos en la entrada anterior, una matriz unitaria es aquella cuya inversa es la conjugada compleja de su matriz transpuesta. [↩]
-
En la segunda nota al pie de la entrada 13 ya presenté las matrices de Pauli, que vuelvo a poner aquí:
 ,
,  y
y  . Con ayuda de estas matrices se puede encontrar rápidamente la matriz de
. Con ayuda de estas matrices se puede encontrar rápidamente la matriz de 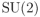 asociada a un cuaternión de la forma
asociada a un cuaternión de la forma  : simplemente hay que sustituir cada elemento de la base de vectores,
: simplemente hay que sustituir cada elemento de la base de vectores,  , por su correspondiente matriz de Pauli asociada,
, por su correspondiente matriz de Pauli asociada,  , y, naturalmente, en la parte escalar introducir la matriz identidad
, y, naturalmente, en la parte escalar introducir la matriz identidad  . Así pues, la matriz que buscamos queda así:
. Así pues, la matriz que buscamos queda así:  .
La condición de unitariedad (normalización) del cuaternión se expresa en que la suma de los cuadrados de sus componentes vale 1:
.
La condición de unitariedad (normalización) del cuaternión se expresa en que la suma de los cuadrados de sus componentes vale 1:  y se traduce en la equivalente versión matricial, no en la unitariedad de la matriz (la “U” de
y se traduce en la equivalente versión matricial, no en la unitariedad de la matriz (la “U” de 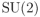 ), sino en que su determinante vale 1 (la “S” de
), sino en que su determinante vale 1 (la “S” de 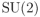 ), como salta a la vista del ojo experimentado que vea la forma de la matriz. Y efectivamente, el producto de dos matrices asociadas respectivamente a dos cuaterniones unitarios produce precisamente la matriz asociada al cuaternión unitario producto de esos dos cuaterniones. Otra cosa muy distinta es la eficiencia de cómputo: multiplicar dos cuaterniones implica hacer 16 productos de números reales, y multiplicar dos matrices 2×2 complejas implica hacer 64 productos de números reales, así que, para evitar redundancias de cálculo por ordenador, es mejor olvidarse de poner los datos ciegamente en una librería de cálculo de producto de matrices, y en vez de ello calcular con cuaterniones en su forma tradicional de cuatro componentes.
[↩]
), como salta a la vista del ojo experimentado que vea la forma de la matriz. Y efectivamente, el producto de dos matrices asociadas respectivamente a dos cuaterniones unitarios produce precisamente la matriz asociada al cuaternión unitario producto de esos dos cuaterniones. Otra cosa muy distinta es la eficiencia de cómputo: multiplicar dos cuaterniones implica hacer 16 productos de números reales, y multiplicar dos matrices 2×2 complejas implica hacer 64 productos de números reales, así que, para evitar redundancias de cálculo por ordenador, es mejor olvidarse de poner los datos ciegamente en una librería de cálculo de producto de matrices, y en vez de ello calcular con cuaterniones en su forma tradicional de cuatro componentes.
[↩] -
En la entrada 13 también definí espinor como un elemento de la subàlgebra par del álgebra
 , y así podíamos identificar a los complejos como los espinores de
, y así podíamos identificar a los complejos como los espinores de  y a los cuaterniones con los espinores de
y a los cuaterniones con los espinores de  . En mecánica cuántica, los espinores que se utilizan para representar la función de onda de un electrón se entienden habitualmente como matrices columna cuyos elementos son números complejos. La conexión entre un tipo de espinores y otro vendría dada por la correspondencia entre vectores de la base ortogonal y matrices de Pauli detallada en la nota al pie anterior. De la matriz 2×2 correspondiente a un espinor del álgebra geométrica se obtiene el espinor de la mecànica cuàntica eliminando la segunda columna de la matriz y quedándose con la primera (la segunda columna de la matriz es reconstruible, como podéis ver si os fijáis en la nota al pie anterior, a partir de las partes reales e imaginaria de los elementos de la primera columna). Los “espinores columna” de la mecánica cuántica, serían algo así como “medias matrices complejas 2×2″, y por tanto, a diferencia de los cuaterniones, ya no pueden multiplicarse entre sí, y se transforman bajo una rotación de rotor
. En mecánica cuántica, los espinores que se utilizan para representar la función de onda de un electrón se entienden habitualmente como matrices columna cuyos elementos son números complejos. La conexión entre un tipo de espinores y otro vendría dada por la correspondencia entre vectores de la base ortogonal y matrices de Pauli detallada en la nota al pie anterior. De la matriz 2×2 correspondiente a un espinor del álgebra geométrica se obtiene el espinor de la mecànica cuàntica eliminando la segunda columna de la matriz y quedándose con la primera (la segunda columna de la matriz es reconstruible, como podéis ver si os fijáis en la nota al pie anterior, a partir de las partes reales e imaginaria de los elementos de la primera columna). Los “espinores columna” de la mecánica cuántica, serían algo así como “medias matrices complejas 2×2″, y por tanto, a diferencia de los cuaterniones, ya no pueden multiplicarse entre sí, y se transforman bajo una rotación de rotor 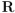 premultiplicándolo por la matriz de
premultiplicándolo por la matriz de 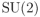 asociada a
asociada a 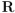 , análogamente al modo en que se compone una rotación de rotor
, análogamente al modo en que se compone una rotación de rotor 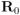 (que haría el papel de espinor a rotar) con la rotación representada con el rotor
(que haría el papel de espinor a rotar) con la rotación representada con el rotor 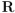 : en vez del producto de rotores
: en vez del producto de rotores 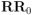 tendríamos el producto de la matriz de
tendríamos el producto de la matriz de 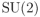 asociada al rotor
asociada al rotor  por el “espinor columna” a rotar. [↩]
por el “espinor columna” a rotar. [↩] -
Bien, se podría objetar que la función de onda (llamémosla
 ), como sabe quien haya estudiado mecánica cuántica, no es en sí algo medible, ya que lo relevante es propiamente el cuadrado de su módulo,
), como sabe quien haya estudiado mecánica cuántica, no es en sí algo medible, ya que lo relevante es propiamente el cuadrado de su módulo,  . Un cambio de signo no sería, pues, físicamente detectable, pero si consideráramos un sistema de dos electrones, y rotamos 360º sólo uno de ellos, el cambio en la función de onda del sistema de dos electrones sí se haría observable. [↩]
. Un cambio de signo no sería, pues, físicamente detectable, pero si consideráramos un sistema de dos electrones, y rotamos 360º sólo uno de ellos, el cambio en la función de onda del sistema de dos electrones sí se haría observable. [↩] -
La demostración rigurosa del teorema de conexión espín-estadística es muy compleja y requiere acudir a conceptos relativistas. [↩]

The Explorando el álgebra geométrica 18 – Rotaciones en el espacio euclídeo tridimensional (III) by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.


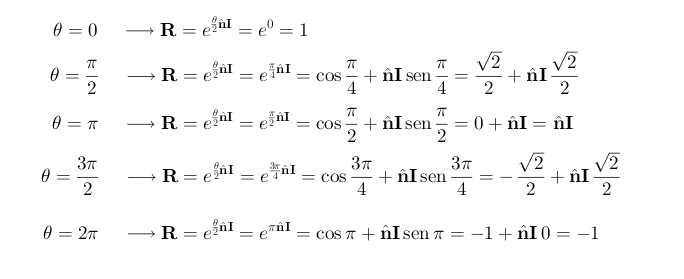




{ 3 } Comentarios
Sólo para saludar y desearles que esten bien de salud, que no es poco en estos tiempos
Me gusta mucho lo que han escrito y creo que es un buen trabajo.
Con un fuerte abrazo virtual
Muchas gracias. Afortunadamente, estoy bien de salud. Por otro lado, este último año he tenido mucho trabajo (trabajo en sistemas de información en el sector sanitario) y no he dedicado casi tiempo al blog. Recientemente me ha surgido algún contratiempo más, por temas familiares. Espero reanudar pronto la actividad con nuevas entradas. Otro fuerte abrazo virtual de vuelta para el otro lado del charco.
Muy buena serie de artículos!!. Estoy deseando por más. Gracias y Saludos!!!
Escribe un comentario