No podíamos pasar por esta serie sin dedicar un artículo a algunos de los juegos más divertidos y paradigmáticos: los wargames.
Empezaremos por el clásico ajedrez y terminaremos por algunos wargames más modernos, aprovechando por el camino para formalizar dos conceptos nuevos, que seguro que hemos empleado mil veces y que ni sabíamos que tenían nombre: la completitud de la información y la perfección de la información.
Ajedrez
El ajedrez es uno de los juegos de estrategia más conocidos y antiguos. Supongo que todos nuestros lectores lo conocen e incluso han jugado alguna vez, pero por si acaso: dos jugadores, uno de ellos con un ejército de color blanco y el otro con un ejército de color negro (aunque se pueden usar otros colores, da igual). Existen distintos tipos de piezas, que representan distintos tipos de unidades del ejército: infantería, caballería, torres, oficiales… cada una con distintos movimientos posibles. El objetivo es capturar al rey contrario. No vamos a revisar las reglas, porque son demasiado complejas para un artículo como este, sino que las vamos a dar por sabidas. Si no las conoces y quieres conocerlas, prueba por ejemplo en el reglamento de la Wikipedia o en el tutorial de monografias.com.
El ajedrez es, entre otras cosas, un juego de información perfecta.
A lo largo de la serie hemos visto otros juegos de información perfecta, como la subasta del dólar o el juego del ciempiés, el problema de las pensiones, el ultimátum… y a todos se nos ocurren otro puñado de juegos más comunes que también son de información perfecta: las damas, el parchís…
También hemos visto un montón de juegos que son de información imperfecta: el dilema del prisionero, dos tercios de la media, los tenistas, escándalo de corrupción…
¿Alguien ve un patrón en la lista de juegos de un tipo y otro?
.
.
.
Todos los juegos de información perfecta son juegos secuenciales. Los juegos simultáneos han de ser necesariamente de información imperfecta, pues hasta que los demás jugadores no anuncian su decisión no la conocemos (cuidado, que lo contrario no es necesariamente cierto; un juego puede ser secuencial y aun así ser de información imperfecta).
Algunos wargames más modernos introducen ideas como estas, por ejemplo permitiendo que los jugadores oculten unidades en edificios o bosques, escribiéndolo en un papel que debe enseñar al oponente cuando quiera mostrar la unidad (sin duda, jugar muchas de estas cosas ahora por ordenador ha facilitado mucho esto).
Resolviendo el ajedrez…
El caso es que, dada una posición (por ejemplo la posición inicial), sabemos cuáles son todos mis posibles movimientos. Dados mis movimientos, sabemos todos los posibles movimientos del oponente, consecuencia de ellos. Y dados esos, sabemos cuales serán los míos en la tercera jugada. Y así sucesivamente, hasta llegar al mate de uno de los jugadores o a las tablas. Es decir, somos capaces, al menos teóricamente, de dibujar el árbol completo del juego. Es decir, conocemos toda la forma extensiva del ajedrez.
Por lo tanto, dado que sabemos que yo eliminaré todos los caminos que me lleven a perder, y el oponente eliminará todos los caminos que le lleven a perder a él, podemos ir podando ramas imposibles, hasta que nos quede solo una decisión posible… y entonces no jugaremos, porque… ¿para qué?… si ya sabemos cómo va a terminar la partida.
Bien, afortunadamente, el número posible de jugadas es del orden de 10^120, un número tan absurdamente grande que probablemente ni te imaginas cómo es. Para que te hagas una idea, se estima que en el universo hay unos 10^79 átomos, así que el número de posibles jugadas es muchos órdenes de magnitud mayor. De modo que, aunque es matemáticamente posible hacerlo, es computacionalmente imposible resolverlo. Por lo que sé, parece que la mayoría de los jugadores IA de ajedrez utilizan algoritmos heurísticos para podar ramas enteras de esos árboles, evitándose calcularlos, para de esa forma encontrar jugadas buenas sin tener que calcular el árbol entero. Así consiguen jugadas mejores que las que conseguimos los simples mortales como yo.
¿No podemos avanzar más? ¿Dejamos ya el artículo? Pues no, porque podemos atacar algún otro juego de estrategia un poco más sencillo. Por ejemplo el tic-tac-toe.
Tic-tac-toe
Una partida atípica de tic-tac-toe
Todos hemos jugado de pequeños, seguro, al tic-tac-toe (en España lo conocemos más como “tres en raya”). Tenemos un tablero de 3×3 casillas, donde un jugador va poniendo cruces y el otro va poniendo círculos. El objetivo es poner 3 de tus fichas en línea antes de que lo haga el contrario.
No me he puesto a hacer los cálculos de los posibles movimientos, pero la Wikipedia dice que hay 138 posibles partidas (obviando las que son rotaciones e imágenes especulares unas de otras), así que muchos valientes se han dedicado a buscar la decisión óptima de cada jugador ante cada situación.
A mí me encanta, por el valor friki, la versión que ha publicado Randall Munroe en xkcd.[1] La imagen tiene detalles muy pequeñitos, así que pica en la imagen para verla en grande si lo necesitas (cuidado, porque la última vez que lo miré con cuidado, me pareció ver una errata en uno de los movimientos, aunque ahora no recuerdo dónde; sí recuerdo que no afectaba a la rama principal, solo a una de las que se descartan).
No es difícil darse cuenta de que, si cada uno de los jugadores hace una partida perfecta (siempre hace su movimiento óptimo en cada momento), el resultado será el siguiente (no olvides que estamos considerando iguales todas las versiones rotadas y especulares de cada posición):
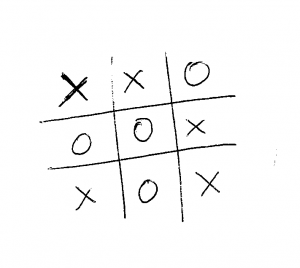
Solución del tic-tac-toe
Es decir, un empate. Algo que, sin tanta parafernalia, ya aprendimos de niños a base de experiencia. Al principio jugábamos contra nuestros amigos, pero al poco tiempo ambos sabíamos qué movimientos no podíamos hacer, de modo que siempre empatábamos. La única solución factible cuando ambos jugadores saben jugar es el empate. Así que dejábamos de jugar.
¿Podemos escalar este resultado a un wargame más complejo? ¿El ajedrez? ¿El Risk? ¿Una guerra real?[2] Pues depende. Dependiendo del juego, si ambos jugadores hacen una partida perfecta (sin errores, eligiendo siempre la mejor decisión en cada movimiento) se puede llegar a una de las siguientes situaciones:
- Juego determinista:
- El juego solo puede acabar en tablas. Por ejemplo, el tic-tac-toe o las damas.
- El juego solo puede ser ganado por uno de los jugadores. Por ejemplo, en el Nim o en Conecta Cuatro siempre gana el jugador que empieza.
- Juego con azar (dados, cartas…):
- El juego se resuelve estadísticamente en tablas. Por ejemplo, el parchís. Si todos los jugadores son perfectos, solo los dados marcan la diferencia.
- El juego beneficia estadísticamente a un jugador. Por ejemplo, en la mayor parte de juegos de casino, estadísticamente gana la banca.
La Wikipedia tiene una lista muy chula de juegos que están resueltos. Ni que decir tiene que el hecho de que un juego esté resuelto no quiere decir que debamos dejar de jugarlo, porque salvo para juegos triviales como el tic-tac-toe o el Nim, no haremos una partida perfecta, y entonces sigue siendo divertido averiguar quién de los dos se aproxima más a ella.
Risk
Por si no has jugado nunca al Risk, te explico muy por encima de qué trata. Es un juego de estrategia, por turnos, en que los jugadores mueven ejércitos desde sus territorios a los territorios enemigos, resolviéndose cada batalla según unas tiradas de dados.
¿Cuál es el objetivo? Pues depende. No, el objetivo no es conquistar el mundo. Al empezar, cada jugador saca una carta de objetivos de un mazo y la mantiene secreta. Los objetivos pueden ser “conquistar 20 territorios” o “conquistar 3 continentes cualesquiera” o “conquistar Sudamérica y África” o cosas así. Cuando un jugador ha conseguido su objetivo, enseña su carta de objetivo a los demás jugadores y ¡ha ganado!
Es decir, es un juego de información incompleta.
Hay aquí dos detalles importantes: “todos los factores del juego” y “conocimiento común”.
“Todos los factores del juego” incluye el número e identidad de los jugadores, sus objetivos, sus posibles decisiones, las recompensas de cada combinación de decisiones… y muchas cosas más. Todo.
“Conocimiento común” significa no solo que todos los jugadores conocen esos factores del juego, sino que además todos saben que todos los conocen, y todos saben que todos saben que todos los conocen, y todos saben que todos saben que todos saben que todos los conocen… y así hasta el infinito.
En el caso del Risk, los jugadores no conocen los objetivos de los demás jugadores. Es difícil diseñar wargames en que exista incompletitud de la información (al menos, es difícil que la incompletitud sea algo más que los objetivos), porque ambos jugadores pueden leer el reglamento del juego. Pero en la vida real, como ya hemos visto alguna vez, los grandes ganadores han sido quienes encontraban nuevas decisiones posibles, cambiaban las recompensas, ocultaban cosas al oponente…
Hemos visto algunos juegos de información completa, como el dilema del prisionero, la caza del ciervo o la guerra de sexos. Y también algunos juegos con información incompleta, como el escándalo de corrupción (decíamos que la matriz de pagos era una estimación, pero no sabíamos si el oponente manejaba otra distinta, o si la nuestra era correcta) o la subasta del dólar (no sabíamos el valor que cada jugador le estaba dando al dólar, ni cuántos jugadores había, ni prácticamente nada).
Y más importante: hemos visto juegos que parecían de información completa… pero luego empíricamente se demostraba que no lo eran: el ejemplo paradigmático ha sido el juego del dictador (refréscalo si lo tienes viejo). Con el juego tal y como lo enunciamos, era obvio que la solución del juego era que Ana se quedaba con 100€, pero… el caso es que no, Ana no siempre se quedaba con 100€. Alguna recompensa oculta había en el juego que hacía que Ana eligiera otro valor a veces. Parecía de información completa, pero no lo era.
O incluso buceando más, continuamente hemos estado diciendo que a menudo nos confundíamos de juego, porque parecía que estábamos jugando a una determinada cosa, cuando en realidad estábamos jugando a la evolución. Fíjate si era incompleta la información que no es solo que no conociéramos todos los factores del juego, sino que ni siquiera sabíamos a qué juego estábamos jugando. Algunos incluso dirían que ni siquiera sabíamos que los jugadores no éramos nosotros, sino nuestros genes.
Esta es precisamente la mayor crítica que se le hace a la aplicación de la teoría de juegos a la vida real. Para poder hacer un análisis abordable, a menudo hay que suponer que tenemos un juego de información completa, lo resolvemos, encontramos la mejor decisión y luego aplicamos esa decisión a la vida real. Si la suposición era lo bastante aproximada, puede que la conclusión sea aplicable a la vida real, pero si no…
El caso es que la vida real raramente es de información completa ni de información perfecta. No conocemos las motivaciones de nuestros compañeros de trabajo, no sabemos la recompensa que va a obtener nuestro cliente al comprarnos un producto o servicio, no sabemos las órdenes que ha dado el general enemigo, no sabemos si hay más jugadores a los que no estemos teniendo en cuenta, ni siquiera estamos seguros de estar jugando al juego adecuado… ¿quién dijo que la vida fuera fácil? Si de verdad la vida fuera un juego de información completa y perfecta… ya hemos visto en qué acaba el tic-tac-toe en ese caso…
- Uno de los mejores cómics de Internet. Si no lo tienes agregado a tu lector de RSS, ya estás tardando. [↩]
- Ya hemos visto que Joshua sí aprende algo de jugar al tic-tac-toe. ¿Aún no has ido aún a ver la película? ¿Pero a qué estás esperando, alma de cántaro? [↩]

The Teoría de juegos XXIX – Wargames by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.









{ 6 } Comentarios
Excelente artículo, justo acabo de terminar de leerme la serie completa ^_^ (y verme la película: WarGames)
PD: Ya encontré un error al tic-tac-toe de Randall, y es en:
x| |o o|o| x|x|xEn el cuadro de las jugadas optimas para las Xs (tercera columna, primera fila-> primera columna, segunda fila->segunda columna, segunda fila)Aunque la vida real fuera un juego de información completa y perfecta. Nunca terminaría en empate. Siempre ganarían los mismos, los poderosos. Ellos crean el tablero, las reglas y los objetivos. Y si no ganan pues modifican lo que haya que cambiar para ganar. Y lo mejor de todo es que convencen a los perdedores de que la culpa es suya por perder o que les han ganado por su bien, y los derrotados se lo creen.
Arriba Deep Blue??….. O arriba los programadores que de dieron su “inteligencia”??
¿Como realizas búsquedas en un número como 10^120?
Saludos
@Juan Carlos: Deep Blue, un RS/6000 basado en AIX con (creo recordar) como 1024 CPU’s, en su día fue un ordenador muy potente (ahora sería una castaña, pero es que la ciencia avanza una barbaridad).
Sin embargo, el programa que tenía, hecho ad hoc, no era nada del otro mundo: mucha fuerza bruta y muchos billones de jugadas analizadas, pero poco talento. En su primera versión Kasparov le barrió con facilidad, aunque perdió una partida, muy celebrada por la prensa y por IBM en su momento. El motivo de perderla fue que el gran Kasparov se empeñó en plantearla abierta, con muchísimas combinaciones posibles. Era un terreno en el que Kasparov se movía como pez en el agua y hubiera ganado a cualquier humano, pero es justo donde una computadora que analiza millones de jugadas por segundo es imbatible… El resto del torneo planteó siempre partidas cerradas (Ben-Onis, Indias de Dama y cosas así) y destrozó a la máquina.
Luego IBM mejoró la máquina, que llamó “Deeper Blue”, duplicando su capacidad y velocidad, y mejoró algo el programa. En el duelo subsiguiente, la máquina ganó 3,5 a 2,5, pero hubo muchísima controversia porque Kasparov se quejó de que “alguien” tenía que estar “sugiriendo” movimientos a la máquina para que hiciera lo que hizo. IBM nunca entregó los logs de las partidas, lo que hace sospechar… Fue un enorme éxito publicitario para IBM y económico para Kasparov, que se embolsó una pasta.
Después fueron mejorando los programas. Y más. Y más. No tienen que analizar “muchillones” de jugadas, sino que usan más las técnicas que usan los jugadores humanos: comparación de patrones, consulta a partidas existentes, etc. Y fuerza bruta, claro.
En estos tiempos ya está claro que no hay nadie en el mundo que sea capaz de ganar sistemáticamente a las mejores máquinas de ajedrez, que ni siquiera necesitan superordenadores para hacerlo: con un buen PC portátil les basta. Así que ya no se hacen torneos hombre-máquina, sino entre hombres entre sí, o entre máquinas entre sí…
El ajedrez ha perdido casi todo su romanticismo… aunque reconstruir partidas de Alekhine o de Capablanca o de Smislov o de Fischer sigue siendo una delicia.
Muchas gracias por la información, Mac!!!
¿En serio hay torneos entre máquinas?… Huy, he estado escondido en la pre-historia mucho tiempo
@Juan Carlos: Pues sí. Hay varios, entre ellos nada menos que un campeonato mundial y todo…
Echa un ojo a esto: http://en.wikipedia.org/wiki/World_Computer_Chess_Championship
Saludos
Escribe un comentario