En el anterior artículo de la serie planteamos un nuevo juego para nuestros lectores: el juego del dictador.

Recapitulemos las reglas: teníamos 100€, y debíamos decidir cuánto de ese dinero nos quedábamos y cuánto le dábamos a Alberto.

Hemos tenido 38 participantes (hasta el viernes a media tarde, en que ya dejé de contar), y el histograma de las decisiones que habéis tomado es el siguiente (medimos la cantidad que cada jugador se queda para sí):

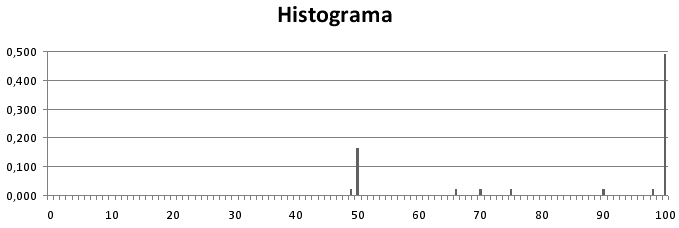
¿Hace falta que os cuente cuál es el resultado teórico óptimo? Por si acaso: Ana se queda con 100€, que es su máximo beneficio, y a Alberto que le den.

Cualitativamente, era obvio que iba a haber un pico en el 100… lo que quizá muchos no esperaban es que hubiera un pico tan pronunciado en el 50, y muchos valores dispersos entre el 50 y el 100. ¡Incluso alguno por debajo del 50!

¿Por qué tanta discrepancia en este y en otros juegos entre el resultado teórico y el resultado empírico? Eso es lo que veremos en este artículo. Vamos a formalizar otros pocos conceptos que, aunque ya los hemos usado durante la serie, ha sido de manera implícita o informal.

Hombre económico

Este es el concepto de jugador que hemos estado usando hasta ahora implícitamente. Nuestro objetivo, cuando buscábamos la estrategia óptima teórica, era buscar nuestro máximo beneficio. Ojo, que eso no implica la máxima pérdida para el otro (no necesariamente), sino tan solo nuestro máximo beneficio sin mirar el beneficio del otro. Si ese máximo nuestro le da también mucho al otro, pues mejor para él; y si no, pues ajo y agua.

No debe entenderse aquí egoísta en modo peyorativo. La RAE da una definición de egoísmo que resulta muy acertada para el uso coloquial del egoísmo, pero no para el uso que le damos en este epígrafe. Por ejemplo el liberalismo económico se basa, simplificándolo, en que un puñado de compradores y vendedores, buscando egoístamente su propio beneficio, lograrán el máximo beneficio global posible.

Según sigamos avanzando a aspectos más matemáticos de la serie, será este el modelo de jugador que usaremos.

Hombre irracional

Ya presentamos este concepto en la segunda parte del juego de dos-tercios-de-la-media, y ya discutimos bastante allí sobre él, así que lo vamos a dejar de momento.

Hombre social

Este tipo de jugador también lo hemos visto, en la segunda parte del artículo sobre el juego de contar. Como veíamos allí, muchos autores sostienen que estos jugadores en realidad no existen, y que, si parece que existen, es porque sus genes están jugando al juego competitivo de la evolución. De ese modo, la evolución elimina a los jugadores que no se comportan de manera social sino egoísta. La sociedad desprecia el egoísmo (hasta tal punto es así que, como hemos visto, el significado de egoísta según la RAE es bastante peyorativo; por ejemplo, hemos visto en el juego del ultimátum que los Albertos tendían a castigar a las Anas que proponían un reparto poco equitativo) sin darse cuenta de que ese comportamiento social es evolutivamente egoísta.^[2]

No obstante, y a pesar de ello, dependiendo de lo que estemos estudiando puede interesarnos simplificar y centrarnos en el jugador social del juego que estemos estudiando, olvidándonos del juego que tenemos por encima.

Según un hombre social, un beneficio de 5,5 será mejor que un beneficio de 7,0, porque aunque en la segunda opción él gana más (7 frente a 5), en la primera la suma es mayor (10 frente a 7).

Si recordamos el juego del ciempiés, nos acordaremos de que el resultado empírico era muy distinto del teórico esperado si utilizábamos la hipótesis de hombre económico (que era la que decíamos que era óptima teóricamente, ya que estábamos implícitamente diciendo que nuestros jugadores eran egoístas). Y también vimos en la segunda parte del artículo sobre el juego de contar que la explicación de que los jugadores eran irracionales tampoco era satisfactoria.

Pues aquí tenemos otra explicación, que algunos consideran la más satisfactoria: los jugadores del juego del ciempiés son hombres, con sus defectos y sus virtudes, y nuestra especie es un jugador social. No solo es que cada jugador se comporte como hombre social, es que cada uno de ellos asume que su oponente también es un hombre social, y piensa “bueno… probablemente no va a cortar al principio, porque si sigue ganamos mucho”, y entonces la mejor estrategia no es repartir en el turno 1. Si el otro piensa lo mismo (lo cual es bastante plausible, dado que es también un ser humano), ambos ganaremos más.

El problema es que esa mentalidad está tan arraigada en nuestros genes que a lo mejor ni hemos pensado en ella. Por ejemplo, cuando el ínclito Macluskey editaba los artículos de esta serie, me decía por email: “si fuera yo, seguía siempre hasta el turno 100 y desplumábamos a la banca“. Fijaos en que su conclusión no era “y me forro” sino “y desplumamos a la banca“, en el sentido de que la banca pierde el máximo: es decir, la suma de ambos jugadores gana el máximo.^[3]

Así, al menos durante los primeros turnos, cada uno de los turnos debe hacerse como un jugador social. Por ejemplo, si en el turno 5 Interrumpo, yo gano 6 y el otro 4. Pero si paso, y el otro interrumpe, yo gano 5 el otro 7. Yo gano menos, pero entre los dos ganamos más. Si en el turno 6 el oponente hace el mismo razonamiento, llegaremos al turno 7, y yo lo haré otra vez, y él otra, y otra y otra. Como ambos somos hombres sociales, probablemente haremos el mismo razonamiento (incluso sin pensarlo mucho) y ambos ganemos más. Nos diremos “jo, si este tipo colabora, nos forramos”.

Podrás imaginar que la situación tampoco tiene por qué ser “todo o nada”. Y por eso no reparte en el turno 1 o en el 100, sino que puede (suele) ser algo intermedio. Unos llegarán hasta el turno 100, otros cortarán en el 1 y la mayoría en algún lugar intermedio. Pero en cualquier caso, parece obvio que las especies que son jugadores sociales tienden a imponerse sobre las que no: el ser humano sobre los felinos de la sabana, los lobos que cazan en manada sobre las manadas de ciervos, los seres pluricelulares sobre los unicelulares,… Y todo ello a pesar de que un león es capaz de comerse a un humano, un ciervo de cornear a un lobo y un virus de matar a una célula humana.

¿Por qué? Porque como veíamos en artículos anteriores, en realidad existe un jugador egoísta en un juego superior (por ejemplo, nuestros genes en el juego de la evolución) que nos obliga a comportarnos como jugador social en este. Este juego es paradigmático: para ganar lo máximo en el juego completo (egoísmo), lo mejor es ser social turno a turno (al principio al menos).

Veremos más adelante (quizá dentro de ocho artículos) que el hombre económico también puede aprovechar ese conocimiento para maximizar su beneficio, aunque no de manera tan sencilla como veíamos inicialmente, y a lo mejor eso es lo que están haciendo inconscientemente nuestros jugadores empíricos.

También profundizaremos dentro de 2-3 artículos en la idea de que el comportamiento egoísta y el comportamiento social pueden ser en realidad el mismo.

Algunos autores llaman a ese comportamiento hombre superracional, en el sentido de que son racionales en un nivel superior: si ambos son superracionales, ambos ganarán más. En mi opinión no es exactamente lo mismo: un jugador social antepondrá la ganancia de la sociedad a la suya propia, mientras que uno superracional lo hará únicamente si eso supone que, haciendo el otro lo mismo, ambos ganan más. Creo que al final, evolutivamente, es lo mismo, pero quizá cada uno pone el énfasis en un sitio distinto. En cualquier caso, más adelante volveremos a darle vueltas a esto.

Hombre altruista

Este comportamiento lo hemos visto en los comentarios del juego del dictador, que daba pie a este artículo: teníamos 100€ y debíamos decidir cuánto nos quedábamos y cuánto le dábamos al otro. Aunque muchos jugadores ha decidido quedarse los 100€, muchos otros han decidido repartirlo de una forma más equitativa (como antes, no tiene por qué ser 100% altruista, sino que será en un cierto porcentaje egoísta y en cierto porcentaje altruista).

Nótese que este caso no es el mismo del hombre social. Como hemos visto, el hombre social elegirá 5,5 antes que 7,0. Pero es que el hombre altruista elegirá 5,5 incluso antes que 10,0 o hasta que 11,0.

En Internet, nadie sabe que eres un perro (Peter Steiner, en The New Yorker, 1993)

Hay varias posibles explicaciones (y supongo que la correcta es una mezcla de ellas):

• Un error en el diseño del experimento: la distorsión del encuestador. Los jugadores, al saberse observados, no dicen lo que realmente harían si no hubiera nadie viéndoles, y sesgan el resultado hacia el comportamiento socialmente aceptado. Dado el anonimato de nuestros comentarios, esperaba que este efecto se disipase un poco (ya sabéis, en Internet nadie sabe que eres un perro), pero lo cierto es que quizá también tenemos una “reputación digital” que mantener, y de hecho algunos jugadores han dado explicaciones (casi excusas) de por qué daban 0 a Alberto, ¡como si estuviéramos juzgándoles! … Bueno… quizá en cierto modo sí lo estamos haciendo, ¿no?
• Existe alguna recompensa que no estamos teniendo en cuenta. Por ejemplo, un jugador puede sentirse bien consigo mismo si realiza un reparto más equitativo que 100,0. Por ejemplo, si realiza 50€,50€, se siente satisfecho consigo mismo (sus glándulas empiezan a segregar endorfinas o alguna cosa así) y recibe un pago de 2 adicional, de modo que en realidad el pago es 52,50. Nótese que en el 50 puse intencionadamente el símbolo del Euro para indicar que era un pago monetario, pero en el 2 no lo he puesto para indicar que es un pago no-monetario. Así, habríamos reducido la discusión a la del hombre social del epígrafe anterior (que a su vez probablemente es un caso de hombre egoísta en el juego de la evolución). Como ejemplo de este comportamiento, alguno de nuestros jugadores decía que “prefiero dormir tranquilo” o “no se sabe las vueltas que da la vida” (es decir, en realidad está esperando un pago futuro) o quería que Alberto le invitara luego a las copas con lo que le había dado.
• El valor de las recompensas no es igual para todo el mundo y no nos habíamos dado cuenta. Por ejemplo, una persona de renta alta podría no valorar en mucho unos pocos euros, pero sí creer que le serán mucho más útiles al otro, si no tiene renta tan alta. Así, si se queda todo, el pago será 60,0 (ya que 100€ para él tienen un valor de 60; de nuevo, la falta del símbolo del euro es intencionada)^[4] mientras que si le da 70€ al otro, él cree que el valor para el otro será mayor, como por ejemplo 20,70 (los 30€ que se queda valen 20 para él, pero los 70€ que le da al otro valen 70). De este modo, otra vez queda reducido al estudio del hombre social.

Como vemos, todas las explicaciones pasan por el hecho de que el experimento está mal, bien porque influimos en él, bien porque no estamos midiendo lo que creemos.

Que el altruismo exista o no, es motivo de discusión profunda entre los estudiosos del tema, así que por nosotros lo dejaremos aquí.^[5]

Hombre malvado

Ya desde Platón se decía que el hombre malvado solo era malvado porque no conocía las verdaderas consecuencias de sus actos. Así que no os sorprenderá si digo que para muchos este tipo no existe: o bien es simplemente un hombre irracional o bien existe alguna recompensa que no estamos teniendo en cuenta.

Por lo tanto, con este epígrafe no nos referimos al ladrón que roba 1.000.000€ del banco para pegarse la gran vida. Eso sería un hombre económico, que ha sopesado la potencial recompensa y el potencial castigo si le pillan y simplemente ha decidido lo que mejor le venía. Seguro que alguna vez has oído lo de “todos tenemos un precio“… pues eso.

Tampoco nos referimos al gamberro que rompe una marquesina de autobús o al troll que estropea una sana discusión en un foro,^[6] pues esos también tienen recompensa: las endorfinas (o lo que sea) que produce su cuerpo al realizar la acción, o el status ganado ante sus amigos, o alguna otra ganancia, compensan para ellos la pérdida de la sociedad, así que su recompensa es mayor haciendo eso que quedándose quietecitos.

Por ejemplo, cuando jugábamos a “dos-tercios-de-la-media“, Alb dijo un número altísimo intencionadamente… pero tampoco nos referimos a él, porque parece ser que su estrategia involucraba jugar iteradamente y utilizar esa “bravuconada” para condicionar futuras decisiones en futuras iteraciones del juego. Imaginad al niño recién llegado al colegio que el primer día agarra a cualquiera en el recreo y le da una somanta de palos, solo para dejar clara su posición… pues eso tampoco es la maldad a la que nos referimos, porque es una estrategia para el futuro.

Nos referimos a quien hace el mal por sí mismo…

Como antes, no existe consenso sobre si el hombre malvado existe o no. Desde luego, no parece que haya muchos ejemplos (si hay alguno) en que no se pueda hacer corresponder sobre uno de los comportamientos anteriores.^[7]

El problema de las pensiones, revisitado

Así que ahora volvemos a estudiar el problema de las pensiones (reléelo si no lo tienes fresco). Allí vimos que, como hombres económicos, había dos decisiones posibles:

• Si el juego iba a terminar en algún momento o el pago futuro decaía, lo mejor era Interrumpirlo ya.
• Si el juego podía continuar indefinidamente, lo mejor era Continuarlo siempre.

Pero ahora debemos añadir el hecho de que el ser humano, para bien o para mal, no es solamente un hombre económico.

Si creemos que el juego se va a acabar, lo mejor parece ser Interrumpirlo ahora.

Si lo Interrumpimos ahora probablemente dediquemos nuestros recursos a cuidar de nuestros padres de todos modos,^[8] sea por el componente social o por el componente altruista. Eso tiene un coste para nosotros. Supongamos que ese coste es X (ojo: X puede ser mayor o menor de 100, no lo sabemos).

Así que si Continuamos el juego, estaremos pagando 100 y puede (o puede que no) que cobremos 200 en el futuro. Es decir, puede que en neto perdamos 100 o puede que ganemos 100.

Si lo Interrumpimos, no pagaremos los 100, pero de todos modos tendremos que pagar X, porque sabemos que no vamos a dejar tirados a nuestros padres y abuelos. Pero lo que sí es seguro en este caso es que no cobraremos 200 en el futuro. Es decir, en neto, perderemos X.

Incluso si se no Interrumpe bruscamente, sino que el pago futuro va disminuyendo poco a poco como veíamos en aquel artículo, podemos hacer un análisis similar.

Es por este motivo por el que, en mi opinión, sostendremos el sistema público de pensiones, durante un tiempo al menos, incluso aunque creyéramos que en el futuro puede quebrar… al menos mientras que las probabilidades de quiebra en el futuro cercano no sean lo suficientemente altas y/o el pago futuro no sea lo bastante bajo.

Veremos más sobre esas estrategias con probabilidades en futuros artículos.

1. Que no se nos enfaden las damas. Utilizamos el término hombre para indicar la especie, no el sexo. La expresión se traduce del latín homo economicus. [↩]
2. Seguro que nuestros contertulios psicólogos o filósofos, si los hay, pueden confirmarnos cómo dichas disciplinas han dado vueltas a esta idea continuamente a lo largo de la historia. [↩]
3. Nota del tal “ínclito Macluskey”: Conste que sigo pensando lo mismo, ¿eh? [↩]
4. ¿Te parece muy extraño esto? Piensa que si cobras 100€ tendrás que darle 40€ a Hacienda. Si cobras menos, le darás menos; no solo le darás menos en valor absoluto, sino también porcentualmente menos, porque el IRPF no es lineal. El tema ya ha salido anteriormente en El Cedazo. [↩]
5. Una vez más, si hay psicólogos, sociólogos o filósofos en la sala, seguro que pueden aportar algo. [↩]
6. Por ejemplo, cuando jugamos al “dos-tercios-de-la-media”, podría ser que alguno de los números altos fuera de un “jugador malvado”… no lo sabemos. [↩]
7. Otra vez: ¿algún sociólogo/psicólogo/filósofo/teólogo en la sala? [↩]
8. Algo que de todos modos, ahora mismo, muchos ya tienen que hacer, porque las pensiones no son tan altas, pero bueno, dejemos eso, que no es el objetivo de este artículo. [↩]

The Teoría de juegos XIII – Juego del dictador by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.