Hasta ahora hemos utilizado todos los artículos para primero cubrir un juego más o menos artificial, y luego hemos dedicado parte del artículo para contar alguna situación real que pudiéramos hacer análoga al juego.
Hoy vamos a dedicar un artículo completo a una situación real, y a hacerle luego un pequeño análisis: el problema de las pensiones. Primero contaremos cómo es, luego lo plantearemos en lenguaje de la teoría de juegos y lo resolveremos, y luego buscaremos cómo aplicar sus conclusiones al problema real inicial.
Por cierto, no esperéis que encontremos aquí la solución (si fuera tan fácil, alguno la hubiera encontrado ya).[1]
Las pensiones en España
Antes de empezar a tratar el tema, debemos contar en roman paladino cómo funciona el sistema de pensiones en España (quizá debimos haberlo hecho en la serie Entendiendo…). No todos los países tienen un sistema como el nuestro, así que su análisis puede o no ser igual.
El principal gasto de pensiones en España lo supone la pensión de jubilación, que los trabajadores reciben desde que se jubilan (en principio a los 65 años, aunque puede ser a otra edad en según qué condiciones[2]) hasta que mueren. La cuantía de esa pensión depende de lo que el trabajador ganase mientras estaba empleado,[3] del tiempo que haya estado trabajando, de la ley que se le aplique (existen varias leyes distintas activas ahora mismo, dependiendo de si empezó a trabajar en tal año o tal otro), con ciertos máximos y mínimos.
Existen otros tipos de pensión, que apenas afectan al análisis. Vamos a enumerarlos muy someramente, solo para asegurarnos de que las tenemos en cuenta en el juego:
- Pensión de viudedad y de orfandad: como tradicionalmente en España solo trabajaba el varón, si luego moría la familia se quedaba sin ingresos. La pensión de viudedad y la de orfandad las cobran el cónyuge viudo o los hijos, en ese caso. No la vamos a tener en cuenta explícitamente, pero implícitamente estará incluida en la pensión de jubilación. Es decir, si un trabajador lleva cotizando 45 años y se muere con 75, cobrará 10 años de pensión; si en cambio muere a los 65, no cobrará pensión, pero su mujer cobrará la viudedad. Así que de facto está incluido en nuestro juego.
- Pensión de invalidez: se otorga a personas que por motivos de salud no pueden trabajar o tienen algún impedimento para hacerlo: parapléjicos, mancos… Como afecta a poca gente, simplemente la obviaremos y listo.
- Pensiones no contributivas: para poder cobrar las pensiones, hace falta haber contribuido previamente un número de años… bueno, pues como la sociedad no quiere dejar a nadie completamente tirado, existe la posibilidad de acceder a una de estas pensiones (que suelen ser muy muy bajas) incluso sin haber cotizado previamente o no haber cotizado lo suficiente. También las obviaremos, porque aunque su coste no es despreciable, tampoco es tan alto comparado con las demás.
Como decíamos, la cuantía de la pensión de un jubilado se calcula en función de lo que el jubilado ha cotizado previamente, pero el dinero no sale de esa cotización, sino que sale de lo que están pagando ahora quienes sí están trabajando. Es lo que se denomina un sistema de pensiones de reparto.[4]
El juego de las pensiones
Estrictamente hablando, los jugadores son todos los ciudadanos, y es un juego continuo, pero tenemos que simplificarlo un poco.
Así que dividiremos la población en generaciones, y las haremos jugar por turnos. Cada turno, supondremos que hay 3 generaciones:
- La Generación Jubilada (GJ). Es la generación que está cobrando ahora mismo la jubilación.
- La Generación Activa (GA). Es la generación que está trabajando ahora mismo, pagando cuotas a la Seguridad Social, como ya se ha visto en El Cedazo.
- La Generación de Niños (GN). Son los jóvenes que aún no se han incorporado al mercado laboral.
En cada turno existirá:
- Una GN que ni pincha ni corta. Solo la ponemos aquí para remarcar que los jugadores se irán renovando.
- Una GA, que será la única que tome decisiones. Lo más aproximado a tomar una decisión sería votar en las elecciones. En la realidad la GJ también vota, pero de momento vamos a simplificar el juego suponiendo que GJ no toma decisiones. La decisión de GA puede ser:
- C (Continuar): pagar 100 y seguir jugando.
- I (Interrumpir): terminar el juego sin pagar nada.
- Una GJ, que cobrará 200 si GA decide continuar, pero no cobrará nada si GA decide interrumpir.
Al pasar el turno, GJ muere, GA se convierte en GJ, GN se convierte en GA y nace una nueva GN.
Algunos lectores pensarán que el cobro de 200 de GJ es mucho, considerando que el pago de GA es solo de 100. Pero es que no estamos diciendo que eso sean euros. El pago bien pueden ser 100€, pero el cobro no hay que entenderlo solo en términos monetarios, sino también por ejemplo en la tranquilidad de saberse alimentado pase lo que pase, en un momento de tu vida en que no estás en la mejores condiciones físicas para procurarte alimento por ti mismo. Es parecido a cuando veíamos el comercio en el artículo anterior: la misma cantidad de dinero tiene valor distinto para la persona en distintos momentos (y no estamos hablando de la inflación, sino de valor intrínseco; supongamos que los valores monetarios ya están deflactados). Obviamente, el cómo cuantifiquemos eso puede ser muy difícil, pero no afecta de momento a este artículo. Digamos que con una bola mágica de cristal hemos cuantificado eso en 200, y nos vale.
Juego potencialmente infinito
Ya solo nos queda decidir la duración del juego.
Si el juego es potencialmente infinito, estamos ante algo parecido al juego de la confianza (reléelo si no lo tienes fresco, porque utilizaremos algunas ideas robadas de allí). No es exactamente igual, porque allí teníamos dos jugadores que jugaban continuamente hasta el infinito, mientras que aquí el jugador que paga y toma la decisión (GA), se convierte en GJ en el siguiente turno (en el cual cobra) y muere en el siguiente.
En esta variante del juego, solo se acaba el juego si un jugador en el estado GA decide Interrumpirlo. Si no, continuará y continuará.
En este caso, la mejor estrategia de cada GA es Continuar. Pagará 100, pero recibirá 200, así que su ganancia neta será de 100.[5]
Juego finito
Si el juego es finito, estamos ante algo parecido al juego del ciempiés (lo mismo: reléelo si no lo tienes fresco). Tampoco es exactamente igual por el mismo motivo: aquí cada jugador solo decide una vez y juega dos turnos (en el segundo no tiene decisión). Como el juego es finito, cuando acabe, la generación que está en ese momento en GA no pagará nada y la generación que esté en ese momento en GJ no cobrará nada. Supongamos que el juego dura 4 turnos, aunque en realidad el número exacto no importa.
Podría parecer que, visto desde atrás hacia adelante, lo mejor para GA sigue siendo Continuar el juego: seguimos pagando 100 y cobrando 200 en el futuro. Pero el truco aquí es que cobraremos 200 solamente si la generación siguiente a la nuestra decide Continuar. Si la siguiente generación decide Interrumpir, entonces no cobraremos nada cuando seamos GJ.
¿Y por qué iba a querer la generación siguiente a la mía Interrumpir? Que siga el juego, ¿no? Pues sí… hasta el turno 4, en que esa generación ya no puede decidir seguir el juego, porque se ha acabado. Veamos el árbol del juego:
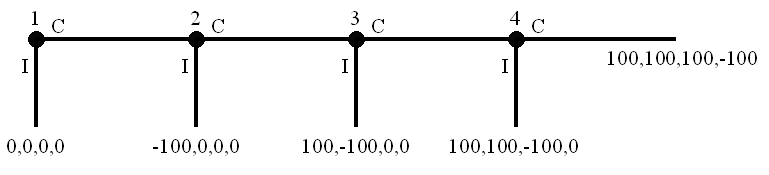
Sobre cada nodo ponemos el jugador que toma la decisión. Nótese que cada jugador solo toma decisión una vez. Aunque siempre es la GA quien toma la decisión, dicha GA es un jugador distinto en cada turno.
Las hojas del árbol son un array con el pago que recibe cada jugador si se sale por esa hoja. Así, si por ejemplo las decisiones son CCI, el jugador 1 ganará 100, el jugador 2 pierde 100, el 3 se queda a 0 y el 4 de hecho ni siquiera llega a jugar (así que 0 también). Nótese que el juego acaba tras el turno 4. Después del turno 4, sea como sea, ya nadie cobra más.
Analicémoslo entonces de adelante hacia atrás.
El jugador 4 puede elegir C (ganando -100; es decir, perdiendo 100) o I (ganando 0, es decir quedándose como está). Obviamente elegirá I.
Entonces, el jugador 3 puede elegir C, que le llevará irremediablemente a perder 100 o I (quedándose a 0). Obviamente elegirá I.
Lo mismo puede razonar el jugador 2, que igualmente elegirá I. Y lo mismo el 1: elegir I.
En este juego, lo mejor es interrumpir cuanto antes.
Juego decreciente
Ni siquiera es necesario que la interrupción sea brusca del tipo “todo o nada”. Por ejemplo, imaginemos que el juego es potencialmente infinito (no interrumpe en un determinado momento debido a las reglas), pero por el motivo que sea el pago a GJ va decayendo. Por ejemplo, empieza en 200, pero decae en 40 en cada generación.
Así, en el primer turno el jugador 1 paga 100. En el segundo turno el jugador 2 paga 100 y el 1 cobra 200. En el tercero, el jugador 3 paga 100 y el 2 cobra 160. En el cuarto turno, el jugador 4 paga 100 y el tercero cobra 120. Y así sucesivamente. ¿Cuál será la ganancia neta del cuarto jugador? Paga 100 en el turno 4 y cobrará 80 en el turno 5: su ganancia neta será -20. Veamos el árbol (tenemos que ponerlo en vertical esta vez porque en horizontal no nos cabe):
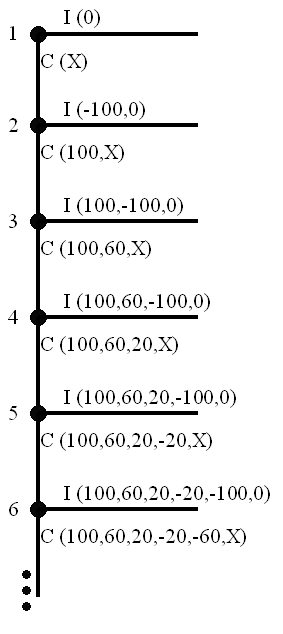
En este caso no podemos poner los pagos en las hojas de terminación, porque al ser potencialmente infinito, existe al menos un caso en que no acaba en una hoja: cuando siempre eligen C y no acaba. Así que cuando se tome una decisión, junto a la decisión pondremos el pago a los jugadores anteriores, marcando con una X las ganancias que no conozcamos aún porque dependan de decisiones posteriores. Por supuesto, podríamos haber especificado también de esta forma un poco especial el árbol de antes, pero queríamos ir introduciendo los cambios poco a poco.
No es difícil darse cuenta de que existe un punto de inflexión en el turno 5. En el turno 5 el jugador 4 pasa de ganar como hicieron sus predecesores a perder (ganancia negativa). Así que el jugador 4, cuando sea su turno de decidir (en el turno 4), tendrá que decir si Interrumpir el juego (obteniendo ganancia 0) o Continuar hasta el turno 5 (donde sabe que incluso su mejor resultado es negativo). Obviamente, elegirá Interrumpir.
Y haciendo la deducción hacia atrás, vemos que si el 4 va a Interrumpir, al 3 le es mejor Interrumpir previamente. Y por lo tanto al 2 le interesa Interrumpir él. Y al 1 le interesa también Interrumpirlo.
El problema de las pensiones
Hemos empezado explicando cómo era el sistema de pensiones en España, luego lo hemos simplificado para poder plantearlo en términos de la teoría de juegos que conocemos hasta ahora, y luego lo hemos resuelto en las tres situaciones posibles:
- Si el sistema continúa indefinidamente, la estrategia ganadora es Continuar siempre.
- Si el juego va a acabarse en algún momento, la mejor estrategia es Interrumpir ya. En este caso, podríamos equiparar la interrupción a una quiebra del sistema de pensiones público.
- Si el pago a GJ va reduciéndose con el tiempo, es equivalente de facto a la segunda opción, y lo mejor es Interrumpir ya. En este caso, podríamos equiparar la reducción a dos cosas (o más probablemente una mezcla de ambas):
- Una reducción real y efectiva de la cuantía de la pensión de jubilación (en términos de dinero constante, una vez tenida en cuenta la inflación).
- Una reducción de la tranquilidad. Decíamos cuando simplificábamos el juego que el pago no había que entenderlo únicamente en términos monetarios (que también), sino en términos de cualquier forma de recompensa, como por ejemplo la tranquilidad de saberse alimentado durante la jubilación. Si tenemos sospechas de que eso pueda no ocurrir, esa tranquilidad se reduce y el pago es menor.
¿En qué situación nos encontramos? Cuidado, porque en función de en cuál situación estemos, la mejor estrategia es sostener el sistema o interrumpirlo. Si leíste el artículo anterior, recordarás que decíamos que confundir un juego de duración infinita con uno de duración finita podía llevar a considerar una “mejor estrategia” equivocada. Ya avisamos al principio del artículo de que no íbamos a dar una solución, solo a plantear el problema en términos de la teoría de juegos.
Es por este motivo por el que el gobierno se empeña, una y otra vez, en demostrar que el sistema de pensiones es sostenible. La simple sospecha de que podría no serlo reduciría el pago equivalente y podría hacernos decidir interrumpirlo antes de que la siguiente generación lo haga y nos “joda” a nosotros.
Por supuesto, aún existe una variable más a tener en cuenta: aunque creamos que vamos a salir perdiendo, ¿debemos sostener a nuestros jubilados? No olvidemos que entre los jubilados se encuentran nuestros propios padres y/o abuelos… ¿les quitamos también la pensión? Veremos más sobre este asunto en los próximos dos artículos. Sé que había prometido que daría mi opinión sobre este asunto… pero será en otro artículo.
- O quizá sí: los lectores de El Cedazo son bastante listos… [↩]
- Justo mientras escribimos este artículo se está planteando ampliarlo hasta los 67 años [↩]
- En realidad, de la cantidad por la que el trabajador cotizase mientras trabajaba, que no es exactamente lo mismo; no nos afecta mucho ese matiz. [↩]
- La alternativa sería un sistema de pensiones de capitalización: los trabajadores en activo aportan dinero a su plan de pensiones de capitalización, ese dinero se ahorra y se invierte sabiamente (se supone), y cuando se jubile cobrará de él. Entonces, los jubilados no cobran del dinero que aportan los trabajadores que están ahora en activo, sino de lo que ellos mismos aportaron hace años cuando estaban en activo. Cuidado, porque en España a menudo se habla de “sistema de pensiones público” para referirse al de reparto y “plan de pensiones privado” para referirse al de capitalización. Aunque habitualmente suele ser así, y de ahí el uso abusivo del lenguaje, nada impide un sistema de capitalización público o de reparto privado. [↩]
- Como ya he dicho en algún momento anterior, formalizaremos este concepto en el futuro, pero de momento válganos la idea intuitiva de que eso es lo mejor. [↩]

The Teoría de juegos XI – El problema de las pensiones by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.





{ 29 } Comentarios
Tal como comentas en los otros juegos, en el tema de las pensiones entra en juego el “hombre irracional”, ya que mucha gente no aceptaría dejar a sus padres sin pensiones, aunque ello les cueste dinero. Así que teniendo muchos jugadores irracionales es imposible jugar racionalmente porque nunca sabes por donde van a salir los tiros.
Fascinante, como toda la serie. Me sigue pareciendo genial como tomas algo teórico y abstracto y lo aplicas a problemas reales (ahí es donde la serie, creo, se sale).
Que yo sepa, la cotizacion no es voluntaria, asi que no es posible dejar de pagar a los jubilados actuales.
El sistema de pensiones no puede ser ,como hasta ahora, autosuficiente. Debe pagarse con impuestos, no con contizaciones.
Y vaya progreso, si cada generación hay que trabajar mas años. ¿ No iban a quitarnos el trabajo las maquinas ?
Xanax:
Efectivamente, la cotización a la SS en España no es voluntaria (puedes revisar un poco más en el artículo sobre la nómina que enlazamos al principio). Tú a título personal no puedes dejar de pagarlo.
Pero en este juego no eres tú a tíluo personal el que juega, sino un jugador ficticio GA que representa a toda la población activa. Por ejemplo, puede decidir votar a un partido que en su programa lleve su eliminación.
Desde el punto de vista económico, no existe diferencia entre Seguridad Social e Impuestos: ambos son una cantidad de dinero que el Estado te quita de tu salario tanto si quieres como si no, y que luego gestiona la administración. La diferencia es solo política.
Bueno… esto no es teoría de juegos, pero puedo contestar algo.
Para empezar te ha cambiado el tiempo que dedicas al trabajo. Mi bisabuelo trabajó desde que tenía 10 años, 15 horas diarias, bajo nieve o sol, 6’5 días a la semana (el domingo por la mañana iba a misa), 12 meses al año, hasta que se murió con 63 años. Trabajó el 50% de su vida de 63 años.
¿Alguna vez has hablado con alguien que tenga vacas lecheras? A la vaca le da igual si es sábado, si es navidad o si es 29/09/10 y has hecho huelga: si no la ordeñas dos veces al día, enferma y se muere. O ya puestos, si se casa tu hijo. Aún recuerdo cuando yo era pequeñito y se casó un primo lejano mío. Sus padres llegaron desde el pueblo justo a la ceremonia (porque tenían que ordeñar a las vacas antes de venir a Madrid) y se fueron corriendo nada más comer, porque tenían que ordeñarlas a las 8 de la tarde.
Yo empecé a trabajar con 21 años, trabajo 8-10 horas diarias en una oficina con calefacción/aire, 5 días a la semana, 11 meses el año, con 15 festivos al año (y eso sin contar con permiso de paternidad, permiso por matrimonio, permiso por familiar enfermo, permiso por mudanza, día de asuntos propios…) hasta que cumpla 65-67 años, y luego seguiré razonablemente sano hasta los 85. El 16% de mi vida de 85 años. De hecho, mi miedo no es que me obliguen a trabajar hasta los 67, sino justo el contrario: que con 55 ya no haya ninguna empresa que me quiera (que es cada vez más habitual en mi sector).
Y eso sin contar con la posibilidad de que te mate con 8 años algo tan simple como el sarampión, una diarrea o una gripe. O que te recluten en una leva a los 16 años y te maten en la guerra.
O con que sufras una enfermedad discapacitante. Antes si tenías esa mala suerte, te jodías y te morías. Ahora te dan una pensión, paupérrima sí, pero mejor que nada.
Yo creo que algo hemos ganado, ¿no?
Y eso comparando con principios del s. XX. Si te vas más atrás, descubrirás que tú vives mejor, más tiempo y más sano que todos los reyes de la edad media.
Pero es que además te ha cambiado el tipo de trabajo. Antes el 99% de la población se dedicaba a cultivar cereales, y solo 1 o 2 hacían ciencia o entretenimiento. Hoy es al revés.
¿Que puede mejorarse? Por supuesto. Pero de ahí a decir que ahora trabajamos más que antes y por lo tanto el progreso es una mierda… no trabajamos más que antes, trabajamos menos y mejor.
Pues aunque no te lo creas, también la teoría de juegos tiene algo que decir aquí (Pedro va a estar encantado). Lo que dices se llama “falacia de suma cero”. Lo veremos por encima dentro de 4 o 5 artículos. La cantidad de trabajo no es constante.
Excelente trabajo, J. Estoy impaciente por que continúes, porque estos bocaditos son tan sabrosos que te dejan con ganas…
@J: Niquelado. El artículo y el comentario.
Iba yo a contestar a Xanax, pero no es necesario. Ya lo has dicho todo.
Saludos, y que siga!
Muy buena y formativa la serie. Bueno el artículo, con la dificultad para el lector de ser objetivo en un “juego” que le afecta sin poder hacer mucho…ya que los que deciden son otros que se han autoasegurado las lentejas. Y muy bueno el comentario. Niquelado tan brillante que me sirve de retrovisor para dar testimonio de buena parte de lo dicho.
En el caso de querer por parar el juego, se podría optar por elegir mantener a tus padres y dejar de pagar pensiones. Llegará un punto en el que esto será más rentable. Claro que los que no tengan hijos o tengan unos indeseables por hijos se fastidian.
Floc. Y si paras puede ocurrir, a la visconversa, que los hijos se queden sin la ayuda que le pueden dar los padres con sus pensiones en largas y negativas coyunturas, y los padres sin el mantenimiento filial tan demagógicamente prometido… O sea, yo votaría (aunque no toca) por no parar y administrar bien aún con cambios a corto plazo impopulares.
Muy buenos días,
No sé si con esto que voy a decir me constituyo en voz disidente o simplemente soy lo que se conoce como “cenizo”, pero por mucho que intente aplicarse la teoría de juegos a la vida real, creo que es como aquellos problemas de física sin fuerzas de rozamiento que nos ponían en el instituto: son idealizaciones o aproximaciones, pero nunca casos realmente reales, valga la “refunfansia”.
En el caso de las pensiones, nunca se va a aplicar únicamente la inteligencia y la racionalidad. El ser humano es compasivo, y eso a veces va en contra de lo meramente racional. Salvo unos pocos elementos humanos, en general no podemos ver sufrir a nuestros mayores, así que si hay que sacrificar dinero para poder darles de comer, aunque ya no produzcan, así va a ser.
Bueno, pues perdón por ser la “cenizo” de la serie, que por cierto estoy disfrutando como un niño en una juguetería. Felicidades.
@Jerbbil: Los problemas de física en los que el rozamiento es cero si sirven, y mucho. Primero para, mediante la simplificación, comprender mejor los conceptos principales del problema (los que realmente entran en juego), y después para llegar a una aproximación lo suficientemente buena para que sea útil. Y digo aproximación, pues existen problemas tan complejos que una solución exacta (real) es tan compleja como innecesaria. Los tiros parabólicos (un disparo) son un problema enormemente complejo que se simplifica según la distancia de disparo y la precisión necesaria (para rifles de francotirador y poder acertar a un blanco a 2Km se utilizan calculadoras especializadas que tienen en cuenta incluso la rotación de la tierra…).
Un saludo
¡Hi @Fernando!
¡¡Pero si yo no creo que los problemas de Física sean inútiles!! ¡Ni muchísimo menos! Al revés, y estoy plenamente de acuerdo contigo; los conceptos quedan muchísimo mejor asentados en la cabecita gracias a ellos. Los mencioné como ejemplo, de por lo visto desafortunada elección, de constructos teóricos que se aproximan a lo real pero no llegan a serlo, por útiles que de todas maneras resulten.
Pues como las pensiones: por muy racionalmente que queramos evaluar su conveniencia o no, siempre entra en juego un factor que nada tiene que ver con la racionalidad y que la teoría de juegos no contempla: la compasión hacia nuestros mayores.
¡Saludetes y buen viernes!
Ejem… llevamos 11 capítulos de unos 30… ya llegaremos, ya. El próximo capítulo, de hecho, podréis volver a jugar vosotros, y profundizaremos precisamente en esa idea.
Yo creo que quizá una mejor analogía sería: un objeto sale disparado hacia arriba con velocidad V0… tiro parabólico… tal y pascual. h=h0+V0t+gt^2. ¡No, porque según la física moderna el tiempo no es continuo, sino cuántico! Bueno… sí… Para ver la trayectoria de un electrón no nos valdrá, pero para ver la trayectoria de un balón sí.
Pues esto es lo mismo: tenemos que seguir profundizando, algunas de las cosas que veremos contradirán a lo que hemos visto, buscaremos otras aproximaciones más allá del simple backtracking… en algunos problemas nos valdrá con una cosa y en otros, necesitaremos más.
De hecho, tengo la impresión de que cuando leas el epígrafe en cuestión de dentro de dos artículos pensarás: “esto J lo ha escrito después de que yo escribiera el comentario”, de lo bien que te encajará. Pues no, ya está escrito desde hace un par de meses. Lo que pasa es que ya os advertí que simplemente pensando podríais llegar a artículos posteriores o incluso más allá de a donde nosotros llegaremos en la serie.
Doy fe. El artículo del que habla J está escrito hace semanas, y ya hemos discutido vivamente él y yo sobre él…
No queda más que esperar unos días, y quedará desvelado el secreto…
Saludos
Muy interesante. Gracias J por acercarnos estas ideas. Siempre había estado interesado en la teoría de juegos, pero la verdad es que no tenía muy claro por donde empezar.
Respecto al modelo de pensiones que presentas, creo que tiene un problema fundamental. Planteas que el grupo GJ no tiene ningun poder de decisión, y que solo el grupo GA es el que decide si continuar el juego. Pero dada la piramide poblacional actual, creo que el GJ tiene un poder de decisión tremendo (son muchos).
Otro refinamiento del modelo es que GA no es un grupo homogeneo y sus intereses son distintos. Yo lo dividiría en dos subgrupos: aquellos que estan lejos de la edad de jubilación y aquellos que estan cerca. Los intereses de este segundo grupo y los de GJ son muy parecidos (continuar jugando), y dado que son mayoría (en la actual distribución de población), parece que el juego esta condenado a continuar indefinidamente.
Por ultimo, el modelo tampoco tiene en cuenta de donde salen los 100 que paga GA. ¿Y si no es posible dar siempre 100? Bueno, pensandolo un poco mejor, esto es equivalente, creo yo, a o bien interrumpir el juego o a que GJ reciba cada vez menos, así que nada, olvida esta parte
De todos modos, supongo que el objetivo de esta entrega no es hacer un modelo detallado y realista de un sistema de pensiones, si no simplemente hacer ver que con unos pocos elementos de teoria de juegos puedes empezar a atacar problemas reales.
Exacto. De este artículo y de todos las de la serie. Al contrario que en la serie Entendiendo, donde intentábamos contar cosas muy prácticas, aquí se trata de ejercicios teóricos y modelos simplificados de la realidad. Pero no creas que por ser teóricos y simplificados no enseñan nada. Si lees el artículo sobre termodinámica que Pedro acaba de publicar verás que en física se hace también simplificaciones para poder estudiar las cosas.
Lo sé, lo sé, que me vas a contar Por eso te agradezco el esfuerzo de introducirnos en esto de la teoría de juegos. Es una pena que en las enseñanzas medias no se hable un poco de todo esto (al menos cuando yo pasé por el instituto, no sé como estará el asunto ahora). Del mismo modo que se enseña física o biología, creo que introducir algo de teoría de juegos en el temario de matemáticas sería estupendo.
Por eso te agradezco el esfuerzo de introducirnos en esto de la teoría de juegos. Es una pena que en las enseñanzas medias no se hable un poco de todo esto (al menos cuando yo pasé por el instituto, no sé como estará el asunto ahora). Del mismo modo que se enseña física o biología, creo que introducir algo de teoría de juegos en el temario de matemáticas sería estupendo.
Acabo de aterrizar en esta serie y me parece sencillamente fascinante. Me incorporo tarde pero expectante por todo lo que está aún por llegar.
Mis sinceras felicitaciones por el planteamiento, el formato, el nivel didáctico, las aplicaciones prácticas… Mira que llevaba tiempo buscando referencias a teoría de juegos, sin encontrar más que unos cuantos ejemplos clásicos, teóricos, insulsos y repetidos en todas partes.
Bien, pues ya encontré lo que buscaba. Enhorabuena y hasta pronto!
Sin remontarme a la edad media, mis padres trabajando solo uno de ellos (fuera de casa) pudieron comprarse una casa en pocos años. Criaron a 4 hijos y se han jubilado a los 65 años.
Hoy, dime cuantos matrimonios pueden hacer lo mismo, trabajando los dos, cuidando de los hijos unas pocas horas y trabajando 50 horas cada uno a la semana.
Si tu trabajas menos y mejor que tus padres y tienes mas poder adquisitivo y mas tiempo libre , enhorabuena.
Elias,
si en vez de discutir sobre las bondades del progreso lo que quieres es discutir sobre las bondades de una reforma de pensiones del PSOE, no voy a entrar en eso, porque en este país cuando entramos en temas políticos siempre acabamos a ostias. Te sugiero un par de blogs si quieres profundizar en el tema.
Este es un abogado laboralista que pone sus pensamientos en un blog. Información utilísima para trabajadores (y para empresarios listillos, que los hay, para que sepan lo que no deben hacer):
http://laboro-spain.blogspot.com/2010/08/beneficiados-por-jubilarse-los-67.html
Estos otros son economistas y se centran más en los aspectos macroeconónimos. Por si te lo estabas preguntando, digamos que… en fin… no son sospechosos de ser partidarios del PSOE (incluso se les ha acusado de lo contrario).
Por ejemplo:
http://www.fedeablogs.net/economia/?p=6832 http://www.fedeablogs.net/economia/?p=6172 http://www.fedeablogs.net/economia/?p=7185
Han tratado mucho el tema, así que si tiras del hilo del blog encontrarás mucha documentación.
El sistema de pensiones es un timo piramidal, que requiere para funcionar que muchísima gente que está trabajando ahora para pagar las pensiones de sus mayores se muera y se quede sin cobrar, y su familia tampoco reciba nada de ese dinero que él ha estado cotizando religiosamente. Peor aún, como es el Estado el que controla el dinero que te corresponde, puede secuestrártelo o cambiarte las reglas a mitad y dejarte con un palmo de narices, como hizo Felipe González y como está haciendo ahora Zapatero. Felipe Gonzalez te amenazaba con dejarte sin pensión si no lo votabas ¡toma ya!
Para el que no lo sepa, fórum filatélico funcionaba EXACTAMENTE IGUAL que la Seguridad Social, así que si eso era una estafa y un esquema piramidal, esto también lo es. Sólo es legal porque lo hace el Estado.
Jeje. Si lo piensas bien, hay muchas cosas que solo son legales si las hace el Estado:
-Si el día 1 de cada mes alguien se quedara con parte de mi sueldo, sería ilegal. Si lo hace el Estado, se llama impuestos. Antes venía el conde y te quitaba una vaca, ahora viene el funcionario y te quita media nómina.
-Si un señor coge y te mete en un cuarto, se llama secuestro. Si lo hace un juez y el cuarto tiene rejas, entonces ya es legal.
-Si mi jefe fotocopia billetes e intenta pagarme con ellos, es ilegal, se llama falsificación. Si las fotocopias las hace el Banco Central, y paga con ellas a los funcionarios del estado, es legal.
Si lo que propones es un sistema de capitalización, como el que explico en la nota al pie, no te creas que eso te libra de la intervención del Estado o del cambio en las reglas del juego. Pueden cambiar las leyes fiscales, puede devaluarse la moneda, puede haber una inflación galopante, el Estado puede quebrar… Si el Estado se declara en quiebra y no hay dinero para las pensiones, ¿qué crees que ocurrirá con los planes de pensiones privados de capitalización? ¿Crees que saldrán de rositas, cuando tienen buena parte de su capital invertido en deuda pública? Todo está conectado. Bienvenido a Matrix.
Abundando en lo que dice J, nuestros colegas europeos de Hungría, que son de la Unión Europea y eso, acaban de “nacionalizar” las pensiones privadas, para pagar deudas del Estado y eso… a saber si quedará algo cuando llegue el momento de jubilarse en Hungría.
Y nuestros todavía más colegas irlandeses acaban de utilizar todo su “Fondo de Reserva” de las Pensiones Públicas para “rescatar” a su sistema económico que se ha ido al carajo porque sus bancos privados están quebrados… a saber de dónde van a cobrar sus pensiones los jubilados irlandeses los próximos años.
Toquemos madera…
Toquemos madera. Mucha madera.
Hola, entro muy tarde a este artículo, os conozco hace poco y me lo paso DPM leyendo, pero en este caso la simplificación es trivial y poco realista. El problema de las pensiones no es por ejemplo el % que se paga hoy y el que se pagará en x tiempo, sino en extrapolar a ese tiempo x (independiente,ente casi de quienes producen y quienes reciben) que crecimiento de riqueza debe/puede garantizarse para mantener el sistema en un entorno razonable. Sin esa proyección la solución es parcial, y si en el momento actual se decide no mantener la de los anteriores, se garantiza perder la de los actuales y no digamos la de los siguientes. Como ejercicio intelectual mola, como ejercicio realista (por el ejemplo propuesto) y aceptando los dogmas actuales, la solución es única y simple: RAVE salvaje, cero crecimiento y suerte al próximo bicho… es decir o el enfoque es la sostenibilidad o a quién se sacrifica… si elegimos el segundo lo mejor es fiesta y game over,
PEPE, ¿crees que no se considera? Precisamente el epígrafe “Juego decreciente” se ocupa de eso, creo.
En cualquier caso, a nivel político comparto tu disyuntiva: o sostenibilidad o elegir a quién sacrificar.
Por favor aceptad mis disculpas, ley deprisa y condicionado de más por la situacion actual. Tienes todo la razón. En mi otra intervención me pasó lo mismo, en vez de interpretarla de forma objetiva y científica, dejé que pesase sobre mi comentario el mundo actual, donde el dinero es de monopoly y el patrón oro paso a ser patron estampita $ despues de que en el 71 Nixon arrasase con los acuerdos de Bretton Woods. Diaculpas de nuevo, me parece magnífico el blog y yo he entrado despistado, no separando realida y opinión personal de información….
Un sincero abrazo y gracias por tan magníficos artículos!!!
Veo un problema en el juego decreciente… esa situación no tiene salida ni para las pensiones ni para nada, de estabilizarse como tendencia todo necesariamente irá decayendo… es interesante y muy instructiva como análisis necesario en teoría de juegos, pero abordada ampliamente desde el ejemplo propuesto… interrumpir en este caso significa colapsar todo… lo suyo es hacer un standby y analizar las condiciones tanto de partida como especialmente los factores externos…
Ante esto sólo hay dos vías: No hay solución si se prioriza el “sistema” actual como inamovible (aparte de soluciones drásticas malthusianas), y la única vía (que no se tomará) es modificar lo que se asume como inamovible… no lo digo en plan místico… no olvidemos que en el entorno real 3/4 partes de la población ni saben lo que puede ser una una pensión… con lo que el futuro es inevitable: Juego decreciente… da igual donde se pare, será un desastre.
Hombre hay una diferencia de concepto entre el conde y el estado, digo de concepto, luego ya en la realidad puede ser otra cosa.
Un conde te imponía los impuestos, o te largaba de sus tierras, sino es que te mataba.
Un estado no deja de ser una contrato social donde la mayoría supuestamente acepta de buen grado contribuir al patrimonio público para gestionar servicios en común, tal que al ser en común debiera salir más barato.
Estadísticamente no querer pagar contribuciones viene del error del ganador de la lotería. Nadie a quien todavía no le ha tocado la lotería quiere pagar la cuota contributiva del premio, la cual si la paga otro es supuestamente un bien común que redunda en ti. ¿Cual es la posibilidad de que te toque la lotería frente a que no te toque? ¿Y por lo tanto no es mejor desde el punto de vista de todos que se pague la cuota?
Por cierto lo que pagamos de seguridad social por cuenta ajena no viene en la nómina sino en los TC o creo que se llaman así.
Que me hace gracia que los empresarios digan que lo pagan ellos, porque si esas cuotas de seguros no fueran al estado, este podría decir que la sanidad y los seguros laborales y la educación no son públicas, y ahora dime con un sueldo, como se va a pagar privadamente esos conceptos sino es incluyendo en el sueldo del asalariado esa parte de cuota de la S. Social y aún se quedaría corto.
Más de 300€ suele ser esa cuota…
Me indignao’. ö Y no soy un jubila’o
Gracias por el espectacular trabajo que hacéis.
{ 1 } Trackback
[...] de juegos XI – El problema de las pensiones, de Javier “J” Sedano, que pode lerse en El Cedazo. Toda a serie Teoría de juegos está publicada en forma de libro, [...]
Escribe un comentario