En la primera parte del artículo planteamos el juego y ahora vamos a ver los resultados y su solución teórica y a aprovechar esa discusión como excusa para presentar algunos conceptos más.
Recapitulemos: se trataba de decir un número que resultara ser dos tercios de la media de todos los números dichos por los jugadores (incluido el nuestro).
Los números que habéis dicho han sido: 1, 1, 1, 1, 1, 1, 2, 5, 7, 7, 9, 9, 10, 10, 12, 12, 13, 13, 14, 15, 16, 18, 18, 18, 18, 22, 22, 22, 22, 22, 22, 22, 25, 30, 32, 33, 33, 33, 33, 34, 35, 40, 42, 49, 55, 69, 87, 97 y 100. La media es 24,755, que multiplicada por 2/3 es 16,503, redondeado a 17, y por lo tanto los ganadores son el “16″ y los “18″: Igor Rodtem, Warsim, Muelle, Jimbo e iñigo.[1]
Por cierto: agradecimientos desde aquí a quienes no suelen comentar los artículos, pero han aprovechado el email para expresar su interés por la serie.
Resultado teórico
El resultado teórico óptimo se puede encontrar por una especie de “reducción al absurdo inductiva“.
Supongamos que todos los jugadores dicen el número más alto posible: 100. La media sería 100 y dos-tercios-de-la-media sería 67. Fijaos en que nunca puede salir un número más alto que ese, así que sería inútil que los jugadores, que pueden hacer esta deducción igual que hemos hecho nosotros, dijeran 100. Todos los números comprendidos entre el 68 y el 100 nunca pueden salir. ¿Por qué van a decir por ejemplo el 91?
Entonces, de facto, el número más alto que pueden decir es 67. Nadie que haya hecho esta reflexión deberá decir nada mayor que 67. Muy bien, entonces, que todos digan el número más alto posible: 67. Si calculamos dos-tercios-de-la-media, sale 45. Uhm… Si todos dijeran 67, que es lo más alto que de facto pueden decir, los dos-tercios-de-la-media saldría 45… entonces, ¿por qué iba ninguno de ellos a decir por ejemplo 55? Lo máximo que deberían decir es 45.
Pero si dicen 45, entonces resulta que dos-tercios-de-la-media es 30. Pero si dicen 30, resulta que…
Puedes imaginar que podemos repetir esto tantas veces como queramos, hasta llegar al 1. Si todos dicen 1, dos-tercios-de-la-media sigue siendo 1, y entonces todos ganan.
Luego el único número que pueden decir es 1.
Muchos de nuestros jugadores han hecho esta deducción y por lo tanto han dicho “1″.
(Espero no haber chafado a Pedro un artículo que estuviera preparando, porque este razonamiento parece propio de los alienígenas matemáticos)
Resultado empírico
El caso es que si repites este juego con jugadores reales, buscando qué sale estadísticamente, raramente sale 1. Y para muestra, nosotros. Nosotros hemos hecho el experimento y no ha salido “1″. No aporta nada que os ponga la lista de nicks con el número que dijeron, pero sí puedo mostraros el histograma.
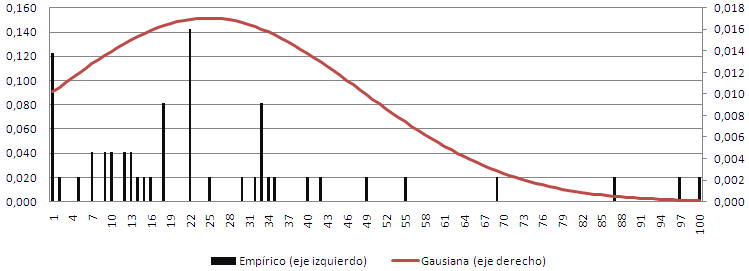
He superpuesto la distribución gausiana (con valores en el eje derecho), aunque en realidad en nuestro caso, con el enorme pico de los “1″ no parezca buena aproximación.
Hemos tenido muchos jugadores que han pensado[2] “la media de 1 a 100… 50… dos tercios… ¡33!”. Otros parecen haber pensado “Uhm… muchos jugadores pensarán eso, así que yo voy a decir 2/3 de 33… ¡22!”; es decir, iniciaban la inducción, pero no la llevaban hasta el final.
El pico del “18″ (que además ha ganado) supongo que se debe a gente que ha pensado lo siguiente: muchos dirán 33, y muchos otros dirán 22″. 2/3 de la media de esos es “18″ [(2/3)*(22+33)/2 = 18].
Alguno incluso habéis dicho números altísimos para los que no tengo explicación. Y una no despreciable cantidad de jugadores se ha ido hacia los alrededores del 10-15, supongo que porque no contaba con los 2 ó 3 jugadores que han dicho números altísimos (durante unos días me pareció que iban a ganar estos).
Confieso que no he intentado ser uno de los jugadores, ni siquiera he intentado preguntarme qué número hubiera dicho yo (y no puedo hacerlo ahora, porque estaría influenciado por el resultado).
No solo es importante que nosotros seamos racionales, eligiendo la mejor opción o no, sino si el otro jugador es irracional o no.
En nuestro ejemplo de dos-tercios-de-la-media, hemos visto que, si todos los jugadores hacen el análisis teórico perfecto, deben decir 1. Pero, ¿qué ocurre si algunos no han hecho ese análisis o lo han hecho mal? Podría ser que acabara ganando uno de esos irracionales, en lugar del estudioso que conoce el problema perfectamente. Es por eso por lo que decíamos que este juego podían jugarlo incluso los que ya lo conocieran previamente, porque no saben qué van a decir aquellos que no lo conocían. Por ejemplo, los editores, Macluskey y Pedro, ya conocían un borrador de esta segunda parte antes de jugar, y no por eso han ganado.
Nótese que aquí no utilizamos el término irracional como sinónimo de tonto. Se puede utilizar ese concepto para cualquier jugador, sea cual sea su inteligencia, que no se haya dado cuenta de cuál era la estrategia óptima, no tenga disponible la misma información que tú, o cualquier otra cosa. Por ejemplo, probablemente algunos de esos números tan altos de nuestro juego han sido personas que leyeron el enunciado apresuradamente y no entendieron lo que se pedía.
En la terminología típica de juegos se suelen decir cosas como “bajo la hipótesis de hombre racional [...] pero bajo la hipótesis de hombre irracional entonces [...]“.
Dedicaremos de nuevo unos párrafos en futuros artículos a este juego, pero de momento lo dejamos aquí para abordar otros desde esta nueva perspectiva.
El juego del ciempiés, revisitado
Echando memoria atrás, probablemente recordemos el juego del ciempiés. Allí veíamos cómo la decisión óptima era repartir en la primera jugada[3], pero los resultados empíricos no acompañaban esa predicción teórica. Si no recuerdas aquel artículo, repásalo, porque seguiremos deduciendo donde lo dejamos.
Aquí tenemos una explicación sobre esa aparente discrepancia: los jugadores de aquellas pruebas empíricas no eran racionales, no hacían el análisis inductivo que nosotros hicimos, y decidían repartir o pasar utilizando otros criterios. Equivocándose, claro.
… ¿O no?
Pues no, no se equivocaban. Porque hay que escarbar más. Podría parecer, leyendo hasta aquí, que si un jugador jugaba al ciempiés y repartía en la primera ronda, era racional, y si pasaba, era irracional… pues no.
Ana, que es racional, podría decirse: “Yo sé que debo repartir en la primera ronda, porque si no, Alberto repartirá en la segunda, pero… ¿lo sabe él? Es decir, a lo mejor Alberto es irracional, y no sabe que en cuanto le llegue el turno debe repartir. ¿Y si me arriesgo? Vale, me arriesgo“.
Resumiendo: si asume que Alberto es racional, debe repartir ahora y llevarse 2€.
Pero si Alberto no es racional, Ana puede pasar, a lo mejor Alberto también pasa y Ana reparte en la 3ª ronda y se lleva 4€.
Fíjate en eso: si Alberto es racional, la mejor opción de Ana es repartir ya. Pero si Alberto es irracional, puede que sea mejor pasar (dependiendo de cuál sea su irracionalidad, que no la conocemos).
Así que Ana, aún siendo racional, pasa en el primer turno.
Pero la gracia es que una vez Alberto tenga el turno, puede hacerse una reflexión similar: “¿Ana ha pasado porque es irracional? ¿O ha pasado porque es racional pero confía en que yo sea irracional? O más aún, quizá ella sospecha que yo sí soy racional, pero cree que voy a hacer este mismo razonamiento y a lo mejor me arriesgo a un turno más“. Ahora Alberto tiene respecto a Ana la misma disyuntiva que Ana tenía antes respecto a Alberto. De modo que, otra vez, el hecho de que Alberto sea racional o no, no significa necesariamente que vaya a repartir. Ni lo contrario tampoco.
Pero es que aún hay más. ¿Y si no es que sea racional/irracional, sino que es racional, pero simula ser irracional para obligarte a cambiar de estrategia?
Es decir, el hecho de que Ana o Alberto sean racionales o irracionales no nos garantiza que deban repartir o pasar, y el hecho de que uno de ellos en un momento dado haya repartido o pasado tampoco nos dice nada respecto a si eran racionales o irracionales. Recordad esta frase, porque es importantísima. Incluso el comportamiento que parece irracional puede ser racional si lo miras con cuidado.
¿Ya te duele la cabeza?
Más aún: si los jugadores racionales reparten siempre en el primer turno, se llevan 2€. Pero parece que los estúpidos que juegan en los experimentos empíricos (en este párrafo sí usamos estúpido en sentido peyorativo y provocativo) no reparten casi nunca en el primer turno, llegando en media por ejemplo hasta el turno 40. En el turno 40 el que repartió se llevó 41€ y el otro 39€. Así que parece que incluso el perdedor de los jugadores estúpidos se llevó 39€ y el jugador racional se llevó 2€… ¿quién es más racional de los dos? ¿Quién más estúpido?
Tengo que recordar aquí la fábula del tonto del pueblo. Todos los días los hombres listos del pueblo convocaban al tonto al bar y le daban a elegir entre coger una moneda de 1€ y otra de 0,50€,[4] y el tonto siempre escogía la de 0,50€. Un día un extranjero que lo vio llamó al tonto y le contó que la de 1€ era de más valor, aunque fuera más pequeña. “Ya lo sé, señor, no soy tan tonto…“, respondió el no-tan-tonto, “…pero si escojo la de 1€, mañana ya no vuelven a reírse de mí y dejo de ganar los 50 céntimos“.
Más adelante en la serie veremos que incluso esta situación tiene solución para el jugador racional, pero no es tan fácil como nos creíamos. Si has leído con atención los párrafos anteriores habrás visto que hemos dicho “…en media…”, y eso te sirve de pista para saber por dónde irán los tiros. También te habrás dado cuenta de que 2+0 es menor que 1+3… otra de las explicaciones que también veremos.
De momento, quedémonos con lo siguiente: la solución que creíamos óptima, puede no ser óptima si admitimos que puede haber jugadores que no sean racionales (aunque no estemos seguros de si nuestro oponente lo es o no, o simplemente él no esté seguro de si nosotros lo somos). Y si puede haber jugadores superracionales (veremos eso más adelante), tampoco.
Por ejemplo, muchos jugadores hicieron el mismo razonamiento teórico que hemos hecho aquí y dijeron “1″, pero luego añadieron “pero claro, no sé si los demás también razonarán esto… a lo mejor no debería decir 1″. Luego no decir “1″ también puede ser racional. De hecho, sé que muchos de los que no han dicho “1″ ha sido exactamente por este motivo.
La suerte del novato
Esto se ve muy claramente en juegos de cartas como el mus cuando juegan novatos. No vamos a explicar las reglas de mus porque son complicadísimas y con muchas variantes locales (revisa la Wikipedia si no las conoces, aunque incluso en ella hay discrepancias respecto a las reglas con que yo juego).
Cuando juegan jugadores novatos (lo que llamaríamos irracionales en nuestra terminología) contra jugadores experimentados (racionales), a menudo, y sorpresivamente, ganan los novatos. A esto se suele llamar la suerte del novato, y aunque a veces es verdad que es debido a la pura suerte a la hora de recibir buenas cartas, la mayoría de las veces es más bien debido al problema que hemos visto: la mejor estrategia cuando todos los jugadores son experimentados (racionales) puede no ser la mejor estrategia cuando no sabemos si hay jugadores novatos (irracionales).
Ejemplo: el jugador novato envida a chica, y se lleva un tanto porquenó. Luego, a pares, el jugador novato echa órdago y el experimentado piensa: “Uhm… qué mamón… lleva buenas cartas, pero ha echado a chica para confundirme… no puedo querer a pares“, porque es lo que él hubiese hecho… Pero no, el jugador novato ha echado órdago a pares con solamente dos pitos, porque no sabe jugar. Y como esa, otro montón de posibles jugadas. El jugador experimentado juega como si el contrincante también fuera experimentado, y eso le lleva a perder. Parafraseando a Macluskey: “la mejor estrategia para el mus es que no descubran qué tipo de jugador eres“.
Ejemplos similares de esta aparente paradoja pueden encontrarse jugando al Texas Hold’em, al tute, a la escoba, al Magic: The Gathering y cientos de otros juegos.
La crisis de los misiles de Cuba
Como tantas otras veces a lo largo de la serie, vamos a buscar un caso real en que podamos aplicar lo que hemos aprendido.
Octubre de 1962. Cuba. La URSS ha llevado varias decenas de misiles nucleares a Cuba, y podría dispararlos estando casi todo EEUU a su alcance. A John Fitzgerald Kennedy, el presidente de EEUU en aquella fecha, aquello no le gusta, porque cambia el equilibrio de fuerzas. Empieza un conflicto y una escalada de violencia.
En la película 13 días[5] Roger Donaldson recrea aquellos momentos. No garantizo que lo que describo a continuación sea justo lo que decían los personajes, porque hablo de memoria, pero mantienen lo esencial.
Los militares proponen a Kennedy invadir Cuba. Creen que eso supondrá que la URSS invada Berlín. EEUU, en ese caso, responderá apoyando a sus aliados según los planes establecidos (planes que incluyen armamento nuclear). ¿Y qué hará entonces la URSS? Según el general, no hará nada, porque lo único que podría hacer es lanzar un ataque nuclear masivo que los destruiría a ambos (y al resto de la humanidad de paso).
¿Y si ese general hubiera seguido adelante y los rusos hubieran hecho la misma deducción sobre los americanos? Es más: la hacen (aunque en la película no nos lo cuentan, debemos deducirlo).Veámoslo.
Kennedy le dice al militar: “Claro que harán algo, nosotros lo haríamos si estuvieran matando a nuestros soldados. No sé qué harán, pero no me diga que no harán nada”.
Así que Kennedy decide no invadir Cuba (de momento al menos), e iniciar un bloqueo. Los rusos saben que si la URSS no respeta el bloqueo, y EEUU hunde un barco soviético, la URSS responderá, se iniciará la escalada de violencia y acabará en una guerra nuclear masiva. Como la URSS sabe que EEUU no quiere esa guerra masiva, también sabe que EEUU no hundirá ningún barco soviético (“¿Cómo quedaríamos si hundiéramos un barco lleno de grano?”, dice uno de los personajes en algún momento). Es decir, han hecho el mismo razonamiento sobre los americanos que el general había hecho antes sobre los rusos. La conversación es algo como:
-¿Qué harán los rusos ahora?
-¿Qué haríamos nosotros?
-Burlar el bloqueo.
-Burlarán el bloqueo.
Como hemos visto, en el juego del ciempiés la mejor decisión cuando el oponente es racional no tiene por qué coincidir con la mejor decisión cuando el oponente es irracional o no sabemos si lo es o él no sabe si nosotros lo somos.
Modifiquemos ligeramente el ciempiés. Ahora pensemos que los montones, en vez de ser monedas de 1€, son millones de muertos. Si interrumpimos el juego en el turno 1, tendremos 2M. Si pasamos, tendremos solo 1M de muertos, pero el otro tendrá 3M. Pero si él entonces también pasa, tendremos nosotros 4M de muertos y él 2M. Y así sucesivamente, sólo que en este perverso juego del ciempiés modificado no hay nadie que lo pare todo al llegar al turno 100…
Analizaremos este caso en próximos artículos de la serie (aunque hay muchos otros en medio).
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 2 |
| 5 |
| 7 |
| 7 |
| 9 |
| 9 |
| 10 |
| 10 |
| 12 |
| 12 |
| 13 |
| 13 |
| 14 |
| 15 |
| 16 |
| 18 |
| 18 |
| 18 |
| 18 |
| 22 |
| 22 |
| 22 |
| 22 |
| 22 |
| 22 |
| 22 |
| 25 |
| 30 |
| 32 |
| 33 |
| 33 |
| 33 |
| 33 |
| 34 |
| 35 |
| 40 |
| 42 |
| 49 |
| 55 |
| 69 |
| 87 |
| 97 |
| 100 |
- Bueno, parece que Igo Rodtem, con el 16, es “más ganador” que los demás si ignoramos el redondeo, pero tal y como describimos las reglas, tanto 16 como 18 son ganadores. [↩]
- Aquí tengo una ventaja sobre vosotros, lectores, y es que muchos jugadores no solo me habéis enviado el número, sino también el razonamiento que habéis seguido para llegar a él, así que a menudo no tengo que especular sobre por qué lo habéis hecho, ya que vosotros mismos me lo habéis contado. [↩]
- Bueno, repartir-repartir no repartía mucho, porque eran 2€ para Ana y 0€ para Alberto… pero se entiende, ¿no? [↩]
- Para quienes no las conozcan, la moneda de 0,50€ es físicamente de mayor tamaño. [↩]
- ¿No la has visto? Ya estás tardando. [↩]

The Teoría de juegos IX – Dos tercios de la media (y II) by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.





{ 13 } Comentarios
Pues sí. A pesar de conocer un borrador de este artículo (y de pensar un poco), no he sido capaz de acertar. Todo ha sido por la extraña proliferación de respuestas desconcertantes (55, 69, 87, 97 y 100), que no sólo no pueden ganar nunca… o no han leído bien el artículo y no se han enterado de qué iba, o si no, no lo entiendo. Pero bueno, al fin y al cabo los animales racionales a veces podemos ser muy irracionales, ¿no?
Así que ajo y agua. He fallado con un mero 100% de error. Otra vez será.
Por cierto: un artículo extraordinario, J. Que además desvela por qué el ciempiés fue tan controvertido en su día…
Yo he dicho 97. ¿Por que?
Primero pense que saldria el 1. Pero pense que el resto de los jugadores tambien lo habrian pensado. A la hora de hacer quinielas no conviene poner el resultado mas esperado, ya que el premios será muy repartido.
Por eso pense que los racionales lectores evitarian dar un numero repetido y buscarian numeros mas elevados. Como todos diran 1, voy a decir 2….. y si todos piensan asi…. mejor digo 3. Cualquier numero racional obtenido mediante una deducion racional, será repetido por alguien. La unica manera de acertar en solitario es dando un numero completamente irracional.
Nadie diria el 97 ya que es completamente irracional y no puede ganar.
¿Por que decir un numero que sabes a ciencia cierta que no puede ganar?
Basicamente por pertubar(por decirlo de manera delicada) todos los razonamientos de los jugadores racionales. La existencia de jugadores irracionales e imprevisibles es la unca manera de poder ganar el juego.
Evidentemente esto solo tiene alguna utilidad si existen varias rondas. ¿Jugamos otra vez?
Alb, por sorprendente que te parezca, también le dedicaremos unos párrafos a eso (que, por cierto, voy a retocar para incluirte).
Fascinante… me ha encantado, aunque no haya ganado, ¡perra vida! Tanto el juego como el análisis. Y lo que más me gusta de la serie, con diferencia, son las referencias a la vida real, con aplicaciones de las conclusiones obtenidas con los juegos. Te está quedando niquelao…
@Alb: Aaaaaahhhh… ya entiendo…. (es que estoy un poco torpe las últimas décadas).
Eso es como cuando a un Madrid-Alcorcón le pones un 2 fijo en la quiniela. Ya sabes que es poco menos que imposible que sea así, pero si por alguna circunstancia extraña, sale… ¡te forras!
Claro que decir “97″ en este juego concreto sólo podría ganar en caso de que todos los apostantes hubieran apostado por un número mayor que 97, y entonces ganar por aproximación (pues si todos dijeran “100″, ¡dos tercios de la media serían 67!).
En una palabra, es como si, en vez de meramente apostar por quién va a ganar el Madrid-Alcorcón (y apostar por un 2 en la quiniela), hubiera que apostar por el resultado, y vas tú y dices que el Alcorcón va a ganar por 4-0. Vale, igual un día de cada quinientos los hados se conjuran con los astros y el Alcorcón va y le gana al Madrid, pero… ¿por 4-0? ¡En la vida se podría dar semejante circunstancia…!! ¿O no?
Ya te espero yo para la próxima, ya…
Saludos. Mac
No puedo creer que casi-acertase. Mi razonamiento sembrara las bases de la psicohistoria! Por cierto, la respuesta correcta deberia ser “2″ ya que su simple eleccion con el resto de participantes como “1″ haria que el redondeo diese como respuesta correcta el “2″, y ganaria el solo, y si todos eligen “2″ la respuesta seria “1.333″ que se redondearia como 2.
Muelle: si todo el mundo pone 1 y tú pones 2, sigue saliendo 1. Imagina que hay 9 “1″ y tu “2″. 1+1+1+1+1+1+1+1+1+2 = 11. 11 /10 = 1,1. 1,1*2/3 = 0,73. Redondeado: 1.
Y si todos eligen “2″, sería 1,33, como bien dices, pero eso redondea a 1.
Mac: (obviando el chiste futbolero) si no he entendido mal el razonamiento de Alb, se basa más bien en que si volvemos a jugar, la gente no se irá ya tanto a números tan bajos, porque como algún capullo diga un 100, les estropea el razonamiento. Y luego va el capullo, dice él el 14 y acierta. Por eso pide jugar otra vez. Si fuera iterativo, no descarto que la estrategia funcionara….
Alb: digo “capullo” en tono provocativo, no pretendo ofender.
J
Rayos!!, mis disculpas, tenia en mente que se redondeaba al entero superior.
Yo fuí uno de los del 33. No es por defender mi posición sino tan sólo por poner encima de la mesa una duda que a ver si alguién me da luz. El juego, tal como se ha desarrollado, ha sido el resultado de una serie de razonamientos cada uno hijo de su padre y de su madre, así que cualquier solución podía ser esperable. Los dos extremos: si uno supone que se cantan los números al buen tuntún, sin razonar la posible evolución, debería salir el 33 ya que todos los números tien la misma probabilidad de ser escogidos. De hecho, en el ejemplo inventado donde se propuiso el juego salía 35. Si aplicabas el razonamiento hasta su extremo más sutil, tenía que salir el 1. Como aquí cada uno pensaba lo que le daba sus meninges, creo que ha salido el promedio de meninges : 1+ 33 = 17. Será una casualidad, pero me parece que la idea de este último razonamiento puede parecerse a la realidad del trasfondo de como se ha desarrollado el juego. Espero comentarios pues no estoy muy seguro de lo que he escrito.
¿ De que sirve acertar si todos aciertan ?
Buenaaaas.
Pues yo fui quien dijo el 40. Me dio en la nariz que el personal diría números más bien bajos, para situarse en los 2/3 de la media, así que quise reventar un poco. Pero ni de broma hice el razonamiento que nos expone J, mis meninges no dan para tanto.
Supongo que lo que expones es válido cuando los jugadores saben o no saben, pero estamos seguros de que juegan limpio (limpio=busco mi beneficio y nada más). Creo que hay una consideración a tener en cuenta: creo que hay un factor “extra”, y que es el mismo que me llevó a mí a decir el 40 o a algún otro apañero a decir números por encima del 70: si no puedo ganar, o no sé cómo ganar, al menos voy a fastidiar al contrario. Pero eso ya escapa de las matemáticas, ¿no?
Saludetes, y felicidades por la serie. Me está gustando un montón.
@jreguart: dita sea, yo también dije 33, apelando a la uniformidad estadística. No me dí cuenta de que aquí ya había algunos expertos y que jugarían racionalmente, evitando los números más altos (aunque tampoco me percaté de que su votación lógica sería 1, no me dio la cabeza para tanto).
Si me hubiese percatado habría aplicado un corrector del 50% (50% de expertos y 50% de inexpertos) y me habría salido 33 / 2 = 16,5, que hubiera redondeado a 16 seguramente.
Como dije, estoy entusiasmado con la serie. Es francamente, genial. La anécdota del tonto del pueblo es que es genial, no la conocía.
Por qué no enseñarán esto en la escuela, en vez de derivadas e integrales que nadie en su sano juicio usará en toda su vida…
{ 2 } Trackbacks
[...] de juegos IX – Dos tercios de la media (y II), de Javier “J” Sedano, que pode lerse en El Cedazo. Toda a serie Teoría de juegos está publicada en forma de libro, [...]
[...] exemplo, na versión orixinal de «dous terzos da media», Alb dixo un número altísimo intencionadamente… pero tampouco nos referimos a el, porque [...]
Escribe un comentario