Tras la breve (bueno, vale, no tan breve) introducción a la serie, hoy empezaré a destripar cómo es la Lógica por el principio, siguiendo los apuntes de la asignatura de Segundo de Carrera que impartió D. José Cuena allá por 1973… Y empezaré, como es lógico, por sus bases más fundamentales. Por el Álgebra de Boole.
Primer día de clase. Octubre de 1973. A la hora en punto aparece el profesor de la asignatura[] y se presenta: “Soy José Cuena, y aunque el nombre de la asignatura es Metodología, yo voy a enseñarles a Vds. Lógica”. Pues vale, ningún problema. Total, un par de horas antes se había presentado el profesor de la asignatura “Informática Básica II”, y nos dijo algo similar: “Como no tengo ni idea de qué hay que dar en esta asignatura, yo les contaré de arriba abajo las tripas del ordenador que yo conozco, que a la sazón es el UNIVAC 1100”… Estábamos en 1973, se trataba de una Carrera nueva, los profesores, que también eran nuevos, eran todos, sin excepción, profesionales que trabajaban en las incipientes empresas informáticas (o que usaban ordenadores, que eran casi igual de pocas) de la época (IBM, Bull, NCR, UNIVAC, Iberia, RENFE, etc), y los temarios de las asignaturas se iban construyendo sobre la marcha. Menuda diferencia con lo que pasa ahora, donde prácticamente ni uno solo de los profesores de las facultades de informática españolas ha trabajado jamás en la empresa privada…[]

George Boole, creador del álgebra que lleva su nombre.
El caso es que D. José (en realidad Pepe para todo el mundo), tras presentarse, comenzó inmediatamente a explicar al Álgebra de Boole []. Rápidamente todos sacamos, aplicadamente, nuestros cuadernos/folios/papeles de tomar apuntes y comenzamos a copiar concienzudamente lo que nos iba explicando.
¿He dicho alguna vez que, en 1973, no había ni un solo libro que pudiéramos usar para estudiar una asignatura de informática? Pues lo digo. Seguramente sí existían libros sobre ciertas disciplinas… ¡en inglés! O sea, como si fuese chino: el “idioma moderno” que estudió mi generación en el Colegio o en el Instituto era français, bien sûr . ¿Y el inglés? Non, pas d’anglais. El poco inglés que yo sabía lo aprendí en una Academia, en cursos de verano, obligado por mi madre (a quien nunca se lo agradeceré lo suficiente, pues mis preferencias iban más por holgazanear, jugar al fútbol e ir a la piscina). Los demás, ni eso. Así que los apuntes tomados de las explicaciones de los profesores y sus gráficos y fórmulas escritos en la pizarra[] eran oro molido, casi el único medio de poder seguir y aprobar la asignatura.
Cedamos, pues, la palabra a Don José:
Sigue leyendo ›






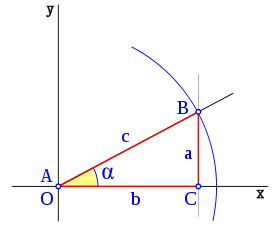








 que 720º. Además, hay una ventaja añadida, sabemos que el seno/coseno/tangente/etc. de cualquier múltiplo o fracción racional de
que 720º. Además, hay una ventaja añadida, sabemos que el seno/coseno/tangente/etc. de cualquier múltiplo o fracción racional de  será
será  . Eso significa que la suma de los ángulos de un triángulo es de
. Eso significa que la suma de los ángulos de un triángulo es de  , y un ángulo recto es de
, y un ángulo recto es de  .
.







