Trigonometría, los enigmáticos triángulos rectángulos II: El seno y el coseno

Hoy, al fin, trataremos con las funciones trigonométricas de las que tanto os he hablado.^[1] En esta serie me voy a centrar en las 6 principales relaciones trigonométricas, a saber:

Triángulo rectángulo sobre el que definir las funciones. Fuente: Seno-Coseno Bajo licencia: CC

$sin \alpha=\frac{a}{c}$ $csc\alpha=\frac{c}{a}$

$cos\alpha=\frac{b}{c}$ $sec\alpha=\frac{c}{a}$

$tan\alpha=\frac{a}{b}$ $cot\alpha=\frac{b}{a}$

Y esas son las funciones que trataremos por pares en los próximos artículos. Algunas de las relaciones entre estas funciones algunos ya las habréis cazado al ver las fórmulas, pero bueno, para eso escribo yo esto, ¿o no?

Claro, yo en esta serie no utilizaré los ángulos de toda la vida, vamos, que la circunferencia ya no va a tener 360º. Eso sí, el sistema angular que voy a usar simplifica mucho algunos cálculos, y es que en esta serie vamos a usar radianes.

Y… ¿qué es un radián? Un radián es el ángulo que tenemos si tendemos un radio de circunferencia sobre la misma. Vamos, que un radián es una medida que te dice como de grande es el ángulo…

Un momento! Imagen obtenida de una captura de pantalla del videojuego "Ace Attorney"

¿Pero eso no te suena?^[2] ¿Eso no nos lo decían ya los grados de antes?

¡Protesto! Fuente: AA Wikia, Licencia Creative Commons

Su Señoría… quiero decir, queridos lectores, eso es.. ¡verdad! Pero, estas medidas tienen algo que no tienen los otros, sencillez en la presentación. Pues no me iréis a decir que no es más cómodo escribir $4\pi$ que 720º. Además, hay una ventaja añadida, sabemos que el seno/coseno/tangente/etc. de cualquier múltiplo o fracción racional de $\pi$ será número algebráico entre -1 y 1.

Cuando trabajamos en radianes, una circunferencia tiene $2\pi rad$ . Eso significa que la suma de los ángulos de un triángulo es de $\pi rad$ , y un ángulo recto es de $\frac{\pi}{2} rad$ .

Desde luego, hay una tasa de conversión entre grados sexagesimales^[3] y radianes, efectivamente, sin la coletilla de grados.

La tasa de conversión en cuestión es la siguiente:

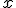De grados sexagesimales a radianes: $x=\frac{360r}{2\pi}$ Donde $r$ es el ángulo en radianes y $x$ el ángulo ya convertido a grados.
De radianes a grados sexagesimales: $r=\frac{2\pi x}{360}$ donde $r$ es el ángulo ya convertido a radianes y $x$ el ángulo en grados.

Al más puro estilo de Pedro en los bloques, voy a proponer en éste y los próximos 3 artículos por cada concepto explicado (en este artículo 3 tandas cortas, en los próximos 2 tandas) un par de problemas sencillos, para aplicar los conceptos adquiridos, que ni que estuviésemos en el colegio.

Y he aquí la primera tanda:

1. Convierte a lo que corresponda los siguientes ángulos: 45º 30º 60º $\frac{3\pi}{2} rad$ $1 rad$ $\frac{\pi}{6}rad$

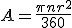2. La fórmula para averiguar el área de un sector circular, dado el número de grados n de ese sector, es $A=\frac{\pi nr^2}{360}$ (teniendo en cuenta que r es el radio y 360º los grados de una circunferencia). ¿Cómo sería la fórmula si el ángulo n viene en radianes en lugar de en gardos?

El Seno

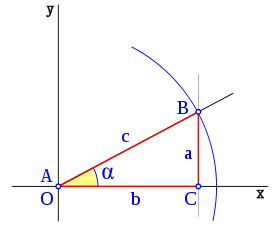
El seno de un ángulo cualquiera es la relación entre el cateto opuesto a ese ángulo y la hipotenusa de un triángulo rectángulo donde esté ese ángulo.^[4]

Los más avispados también habrán notado un detalle, y es que según la fórmula del seno,^[5] el seno de un ángulo “normal”, entendiendo por normal uno que podemos visualizar, no puede pasar de 1 unidad.^[6] También podemos decir que, gracias al Teorema de Tales, da igual cómo de largos sean los lados del triángulo, siempre nos dará el mismo número para un mismo ángulo.

Algún lector ya se estará preguntando con entusiasmo, para darle algún uso práctico, “¿y para qué sirve tener el seno de un ángulo?”. Nada más fácil de contestar, y podemos diferenciar 4 casos con triángulos (análogos para las otras relaciones).

Tenemos solo un ángulo. Bueno, si nos vemos ante este caso únicamente nos queda clavarle con saña el lápiz con el que estamos escribiendo a quien nos haya propuesto el problema, o, preferiblemente, pedir más datos del triángulo.
Tenemos un ángulo y un lado del triángulo a saber. Entonces tenemos el caso perfecto para sacar papel y lápiz y ponerse a calcular, como buen “pro” de la trigonometría que eres. Sabiendo que $sin\alpha=\frac{a}{c}$ y sabes $a$ o $c$ , puedes sacar el resto de lados sin problemas, como ya mostraré en un momento.
Tenemos un ángulo y dos lados. No es necesario usar tus dotes trigonométricas aquí, pero nada te lo impide siguiendo el mismo procedimiento que ahora mostraré.
Tenemos un ángulo y los 3 lados. Aquí sólo cabe preguntar, ¿y el problema a resolver cuál es?

Vale, tenemos el caso 2 (o el 3), ¿cómo procedemos? Fácil, con un poco de álgebra (no, no muerde):

Tenemos la definición primera: $sin\alpha=\frac{a}{c}$

Queremos hallar a:

Para ello, pasamos c al otro lado,

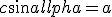
$c sin\alpha=a$

¡Listo!

Queremos hallar c:

Pasamos c,

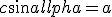
$c sin\alpha=a$

Pasamos $sin\alpha$

$c=\frac{a}{ sin\alpha}$

¡Listo!

Y así, usando solamente unas pocas herramientas básicas algebraicas podemos resolver un triángulo. Bueno, con eso y con el Teorema de Pitagoras, porque, hablando de triángulos, nunca hay que separarse mucho de él.

Y con esto bajo el brazo, vamos, os voy a dar los senos de los principales ángulos (medidos en grados) antes de los problemas:

$0$ º	$30$ º	$45$ º	$60$ º	$90$ º
$0$	$\frac{1}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$	$1$

Y teniendo esto a mano ya estáis listos para los pequeños problemas de senos:^[7]

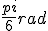3. Tenemos un triángulo rectángulo con una hipotenusa que mide $5cm$ y sabemos que uno de los ángulos mide $\frac{pi}{6} rad$ , ¿Cuánto miden los otros lados?

4. Sabemos que el seno de uno de los ángulos de un triángulo es $\frac{3}{5}$ y que el de otro ángulo es $\frac{1}{3}$ , teniendo en cuenta que el lado opuesto al primer ángulo mide $30cm$ , ¿es un triángulo rectángulo?

El Coseno

Todo lo descrito para el seno también sirve para el coseno, teniendo claras un par de cosas:

El coseno NO es la relación entre el cateto opuesto de un ángulo y la hipotenusa, sino entre el cateto adyacente y la hipotenusa, de aquí salen algunas pistas para deducirlo del seno y al revés.
Para resolver un triángulo con el coseno y luego tener que dibujarlo, hay que tener cuidado y saber bien qué se hace, pues colocar un cateto mal significa darle al seno el valor del coseno, al coseno el valor del seno y, así con el resto de funciones.

Dicho esto, sólo quedan por decir un par de cosas del coseno,la tabla con los ángulos principales, y ya de paso, el procedimiento para obtener esos valores, y una de las relaciones fundamentales entre el seno y el coseno y una de las 3 relaciones cuadráticas.

$\alpha$	$0$ º	$30$ º	$45$ º	$60$ º	$90$ º
$sin\alpha$	$0$	$\frac{1}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$	$1$
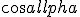$cos\alpha$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$	$0$

Y ahora preguntaréis, “¿y de dónde salen todos esos números?”, cosa que me tendríais que haber preguntado antes con la tabla del seno sólo, pero bueno.

Este pequeño truco que sirve para calcular los principales seno y cosenos:

El caso es que se le asigna un número a cada ángulo, empezando por el $0$ , asignado a $0$ º. Después, para obtener el seno, se hace la raíz cuadrada de cada número y se divide entre dos.

Para obtener los cosenos, sólo hace falta darle la vuelta al orden de los senos, pues, como ya más de uno se habrá dado cuenta, $cos\alpha=sin(\frac{\pi}{2}-\alpha)$ . O lo que es lo mismo, da igual hacer el seno de un ángulo que el coseno del contrario y viceversa.

La primera relación cuadrática

Una relación cuadrática es una igualdad en la cual el máximo exponente es 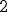$2$ . En este caso, nos encontramos con un poco de Pitágoras, al igual que en el resto, en nuestra primera relación trigonométrica.

La relación de marras es la siguiente:

$sin^2\alpha+cos^2\alpha=1$

Donde $sin^2\alpha$ es el cuadrado del seno de $\alpha$ , y el coseno igual.

¿Pero, os estaréis preguntando, qué viene a decirnos esto? Bien, esa fórmula quiere decir que, el triángulo rectángulo cuyos catetos midan igual que los senos o cosenos de sus ángulos (en ambos casos es lo mismo, recordemos que hemos dicho antes entre senos y cosenos en un triángulo) su hipotenusa medirá $1$ exactamente (no olvidemos que $\sqrt{1}=1$ ). 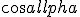También quiere decir que sabiendo $sin\alpha$ podemos conocer $cos\alpha$ sin necesidad de conocer $\alpha$ , usando cuando sea conveniente alguna de las igualdades que salen de esa fórmula, a saber:

$sin\alpha=\sqrt{1-cos^2\alpha}$

$cos\alpha=\sqrt{1-sin^2\alpha}$

Y bien, antes de dejaros los últimos 2 ejercicios y despedirme, algún curioso querrá la demostración de esta igualdad, y aquí la tiene, eso sí, puramente algebraica:

$cos^2\alpha+sin^2\alpha=1$

Sabiendo que $cos\alpha=\frac{b}{c}$ y que $sin\alpha=\frac{a}{c}$ sustituimos:

$\frac{b^2}{c^2}+\frac{a^2}{c^2}=1$

Reducimos:

$\frac{b^2+a^2}{c^2}=1$

Sabiendo que 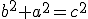$b^2+a^2=c^2$ (Teorema de Pitagoras) sustituimos:

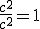
$\frac{c^2}{c^2}=1$

Y como bien sabemos un número entre si mismo es igual a $1$ :

$1=1$

Quedando así demostrada la igualdad.

Y por último, la última tanda de hoy de ejercicios:

5. Unos mineros se han perdido en una mina cuya entrada es una rampa con una pendiente de $60$ º, sabiendo que están a una profundidad de $200m.$ , ¿cuántos metros recorrerá el equipo de rescate desde la entrada de la mina si los mineros están enfrente del final de la rampa?

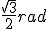6. Si el seno del ángulo $\alpha$ es $\frac{\sqrt{3}}{2}rad$ y suponiendo que estamos hablando de un triángulo rectángulo, ¿cuál es el coseno de ese ángulo? ¿Y el seno del ángulo opuesto?

Nota: El ángulo opuesto a uno dado es el ángulo que se encuentra justo enfrente del ángulo, en un triángulo rectángulo el opuesto a un ángulo dado $\alpha$ es: $\bar{\alpha}=\frac{\pi}{2}-\alpha$

En el próximo artículo trataremos tangentes y secantes, ¿el por qué de esa combinación? Ya lo veréis

Ni que os fuese a presentar a una tía mía… [↩]
Ya estamos otra vez, ¿cuantas veces me tengo que decir a mi mismo que estoy solo? [↩]
a.k.a. “los de toda la vida” [↩]
Con ángulos mayores a $\frac{\pi}{2}$ habría que usar la circunferencia goniométrica, así que no nos fijaremos de momento es esos ángulos [↩]
Y conociendo el Teorema de Pitágoras [↩]
Recordemos que $sin\alpha=a/c$ siendo $a$ el cateto opuesto a $\alpha$ y $c$ la hipotenusa [↩]
No me malpenséis, que nos conocemos [↩]

The Trigonometría, los enigmáticos triángulos rectángulos II: El seno y el coseno by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.

{ 4 } Comentarios

Sergio B | 10/10/2011 at 02:39 | Permalink

Bien bien, hay una regla sencillita para hacer la tabla de conversion a de angulos a su valor en el seno y el coseno, ponemos los angulos, 0º, 30º,45º,60º,90º y para el seno ponemos de 0 a 4, 0,1,2,3,4 y para el coseno al reves, 4,3,2,1,0, y ahora hacemos la raiz cuadrada de todos y dividimos entre 2. Yo al menos la aprendi asi, y la verdad es que aun lo uso, por cierto, lo tienes mal puesto, el coseno de 0º es 1 y el seno es 0.

Con los radianes si que estoy seguro que no hay que poner unidad, sino pone nada son radianes, pero amos, pa que la gente se acostumbre ta bien. ¿Por que usar radianes? Quiza deberias explicarlo un poco mas, no es que sea un capricho. Por ejemplo, al derivar, si son funciones trigonometricas complejas, como no uses radianes, te puedes liar. Hay simplificaciones, que tienen que ser en radianes, por ejemplo el seno de un angulo pequeño es igual al angulo, en radianes, no en grados, que el seno de 1 no esta cerca de 1 esta claro, pero si el de 0.0175 radianes (un grado en radianes), del cual el seno es 0.0175 (hago algunas aproximaciones, pero vamos, que se cumple).
Rafael Miranda Molina | 11/10/2011 at 01:13 | Permalink

Dado que siguen con las tangentes y secantes en el próximo capítulo les dejo un par de sugerencias. Primero ¿por qué se llaman tangentes y secantes? (es bonita la interpretación geométrica); segundo, es interesante notar también la interpretación de la cotangente y cosecante.

Hay un tema bien importante con esto, y es que en varios países se ha tendido a suprimir la trigonometría del currículum escolar, y a mi parecer eso es un error. Al igual que la geometría analítica, existe una visión sumamente utilitaria de la trigonometría, usualmente asociada a la necesidad de enseñar cálculo. Pero ambas dos son áreas problemáticas interesantes en si mismas, más allá de su relación con el cálculo, pues permiten desarrollar estrategias de resolución de problemas valiosas.

En fin, a propósito de matemáticas, ¿has escuchado de los carnavales de matemáticas en español? Te dejo un enlace: http://carnavaldematematicas.bligoo.es/

Saludos desde Chile Rafael
Angel | 11/10/2011 at 11:59 | Permalink

Por si alguien tiene curiosidad en saber de donde salen los valores del seno y coseno de 30º, 45º y 60º, que piense en un triangulo rectangulo isosceles y en un equilatero. Con eso y el teorema de pitagoras se pueden calcular de forma sencilla.
Kratso | 12/10/2011 at 11:08 | Permalink

@Sergio B: Gracias por la correccion de la tabla ^^U . Y, es cierto que no es necesario poner unidades cuando hablamos de radianes, pero nunca está de más, creo yo. Esa regla mnemotécnica es útil sobretodo cuando se comienza con la trigonometría, en principio la iba a añadir, pero tras no encontrar forma de que encajarlo lo deje tal y como está je, je.

@Rafael: mira, no había pensado en ello, me has dado material que agregar al quinto artículo de esta serie(que es cuando tocaremos el apartado más geométrico de la trigonometría). Respecto a lo que dices sobre la paulatina desaparición de la trigonometría en los currículos escolares es bien cierto, hará no más de un par de años, por lo menos en la Comunidad de Madrid, en 3º de la ESO (de 14 a 15 años) era parte del currículo obligatorio, actualmente no se toca la trigonometría hasta bien entrado 4º de la ESO (de 15 a 16 años) y si no he entendido mal, quieren apartarlo del currículo básico y que sea un tema “opcional” que el profesor decidirá si impartir o no, como en esta misma comunidad autónoma ocurre con el temario sobre probabilidad y estadística en 1º y 2º de la ESO. Un claro ejemplo de resolucion de problemas con trigonometría se me presento la semana pasada con un problema en apariencia inocente que me hizo pasar un rato tratando de buscar una solución. Hace unos días le presente ese mismo problema a un amigo y hallo la solucion usando únicamente trigonometría, un desarrollo algo encorroso, pero de una belleza increíble.

El Cedazo