Siguiendo con la serie dedicada al álgebra geométrica, en esta entrada seguiré con las rotaciones que comenzamos a ver en la entrada anterior, pero hablaré del tratamiento, digamos, más convencional de las rotaciones. En los planes de estudio lo habitual es introducir las rotaciones como transformaciones lineales y utilizar las correspondientes matrices ortogonales para representarlas. Sin embargo, en las aplicaciones prácticas el uso de los rotores (cuaterniones unitarios) del álgebra geométrica es de conocimiento obligado por las razones que veremos al final.
La rotación como transformación lineal. Matriz asociada a una rotación
El enfoque matemático habitual para tratar las rotaciones es considerarlas como transformaciones lineales del espacio. Una transformación lineal 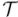 es una aplicación de un espacio vectorial,
es una aplicación de un espacio vectorial,  a otro,
a otro, 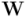 , que cumple esta propiedad:
, que cumple esta propiedad:
Para todo par de vectores  y
y  de
de  y para cualquier par de escalares
y para cualquier par de escalares  y
y 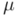 de
de  tenemos:
tenemos:
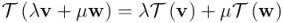
Esta propiedad es equivalente al siguiente par de propiedades:
1) La transformación lineal de la suma de dos vectores cualesquiera es igual a la suma de transformaciones lineales de los vectores:

2) La transformación lineal del producto de un escalar por un vector es igual al producto del mismo escalar por la transformación lineal del vector:

Las transformaciones lineales que nos interesan serán aquellas en las que tanto el espacio vectorial de partida como el de llegada son el espacio vectorial tridimensional,o sea  . Dentro de estas transformaciones lineales tenemos, por ejemplo:
. Dentro de estas transformaciones lineales tenemos, por ejemplo:
1) Las homotecias. Estas transformaciones lineales consisten en multiplicar todo vector de  por un mismo escalar
por un mismo escalar  . Si
. Si 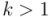 diremos que la homotecia es una dilatación, y si
diremos que la homotecia es una dilatación, y si  la homotecia es una contracción. Efectivamente, una dilatación (o, respectivamente, contracción) de la suma de dos vectores es igual la suma de las dilataciones (o, respectivamente, contracciones) de los dos vectores, y la dilatación del producto de un vector por un cierto factor escalar
la homotecia es una contracción. Efectivamente, una dilatación (o, respectivamente, contracción) de la suma de dos vectores es igual la suma de las dilataciones (o, respectivamente, contracciones) de los dos vectores, y la dilatación del producto de un vector por un cierto factor escalar  es igual a
es igual a  veces la dilatación del vector.
veces la dilatación del vector.
2) Las proyecciones de un vector respecto a otro vector o respecto a un bivector. También se cumple que la proyección de la suma de dos vectores es igual a la suma de proyecciones, así como también que la proyección de un vector multiplicado por un factor escalar  es igual a la proyección del vector mutiplicada por
es igual a la proyección del vector mutiplicada por  .
.
3) Las simetrías y reflexiones. De nuevo aquí se cumple que la simetría o reflexión de la suma de dos vectores es igual a la suma de la simetría o reflexión de cada vector, así como que la simetría o reflexión del producto de un vector por un escalar es igual al producto del escalar por la simetría o reflexión del vector de partida.
4) Como las rotaciones las podemos interpretar como composiciones de dos simetrías o de dos reflexiones, y la composición de dos transformaciones lineales es a su vez otra transformación lineal, se deduce que las rotaciones son transformaciones lineales.
Representación de transformaciones lineales mediante matrices
Una consecuencia de la definición de transformación lineal es que para calcular la transformación lineal de un vector cualquiera basta conocer cuál es la transformación lineal de los vectores de una base del espacio vectorial en que nos encontremos. En particular, como nos encontramos en  , basta conocer la transformación lineal de la base ortonormal de vectores
, basta conocer la transformación lineal de la base ortonormal de vectores  ,
,  y
y  . Si expresamos un vector cualquiera de
. Si expresamos un vector cualquiera de  en función de esta base:
en función de esta base:
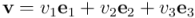
tendremos, al aplicar las propiedades de linealidad, que la transformación  será:
será:

A la hora de trabajar con transformaciones lineales es habitual utilizar el formalismo matricial. Para ello, expresaremos los vectores como matrices columna, de modo que el vector  será identificado con la matriz
será identificado con la matriz  de tres filas y una columna:
de tres filas y una columna:

Fijémonos que al utilizar matrices, estamos presuponiendo una cierta base (en nuestro caso, ortonormal, pero no necesariamente siempre tiene por qué ser así) de vectores, ya que las tres componentes de la matriz columna que representa un vector se refieren a esa base ortonormal en concreto. Otro vector  quedaría representado matricialmente por la correspondiente matriz columna:
quedaría representado matricialmente por la correspondiente matriz columna:
![\\mathsf{w} = \\left[ \\begin{array}{c} w_1 \\ w_2 \\ w_3 \\end{array} \\right]](http://eltamiz.com/elcedazo/wp-content/uploads/2020/02/tex80_deaeb4d4d920424e5a68eb5120779831.png)
Si ahora quisiéramos calcular, por ejemplo, el producto interior  , podríamos hacerlo también utilizando matrices, recurriendo a la matriz transpuesta y al producto de matrices:
, podríamos hacerlo también utilizando matrices, recurriendo a la matriz transpuesta y al producto de matrices:

La transposición de una matriz consiste en obtener una matriz a partir de otra intercambiando filas por columnas. De este modo, la matriz transpuesta de  , que indicamos como
, que indicamos como  , será una matriz fila (tiene una única fila y tres columnas). El producto escalar de vectores puede entonces realizarse, como se puede apreciar, como el producto de la matriz
, será una matriz fila (tiene una única fila y tres columnas). El producto escalar de vectores puede entonces realizarse, como se puede apreciar, como el producto de la matriz  por la matriz
por la matriz 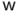 . El producto de una matriz fila como
. El producto de una matriz fila como  por una matriz columna como
por una matriz columna como 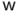 es el caso más sencillo del producto de matrices: para poder hacer el producto es imprescindible que el número de columnas de la primera matriz (3, en nuestro caso) coincida con el número de filas de la segunda matriz. El número de filas de la matriz resultante será el mismo número de filas de la primera matriz que se multiplica (en este caso, 1) y el número de columnas será el número de columnas de segunda matriz (también 1 en este caso). Por tanto, el resultado es una matriz de una fila y una columna, o sea, un número real, que resulta ser el producto escalar euclídeo de los vectores
es el caso más sencillo del producto de matrices: para poder hacer el producto es imprescindible que el número de columnas de la primera matriz (3, en nuestro caso) coincida con el número de filas de la segunda matriz. El número de filas de la matriz resultante será el mismo número de filas de la primera matriz que se multiplica (en este caso, 1) y el número de columnas será el número de columnas de segunda matriz (también 1 en este caso). Por tanto, el resultado es una matriz de una fila y una columna, o sea, un número real, que resulta ser el producto escalar euclídeo de los vectores  y
y  .
.
¿Cómo se representa entonces una transformación lineal de  en
en  ? Sencillamente, se representa con una matriz de tres filas y tres columnas, de modo que la columna
? Sencillamente, se representa con una matriz de tres filas y tres columnas, de modo que la columna  represente el vector resultante de transformar el vector
represente el vector resultante de transformar el vector  de la base, tal como se muestra en la figura:
de la base, tal como se muestra en la figura:

La matriz  representa la transformación lineal
representa la transformación lineal 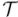 , como podría ser (o no) una rotación. El elemento de la matriz situado en la fila
, como podría ser (o no) una rotación. El elemento de la matriz situado en la fila  , columna
, columna  viene dado por la componente
viene dado por la componente  de la imagen (
de la imagen ( ) del
) del  -ésimo vector de la base que utilicemos. Los vectores se representan por matrices columna, donde el elemento situado en la fila
-ésimo vector de la base que utilicemos. Los vectores se representan por matrices columna, donde el elemento situado en la fila  representa la componente
representa la componente  del vector, según la base utilizada (en nuestro caso, la base ortonormal
del vector, según la base utilizada (en nuestro caso, la base ortonormal  ,
,  ,
,  ). Para calcular la imagen de un vector
). Para calcular la imagen de un vector  cualquiera mediante el formalismo matricial basta multiplicar la matriz
cualquiera mediante el formalismo matricial basta multiplicar la matriz  por el vector columna
por el vector columna  . Para multiplicar dos matrices es necesario que el número de columnas de la primera coincida con el número de filas de la segunda, y el resultado será una matriz con el mismo número de filas que la primera matriz y el mismo número de columnas que la segunda matriz. El elemento de la matriz producto situado en la fila
. Para multiplicar dos matrices es necesario que el número de columnas de la primera coincida con el número de filas de la segunda, y el resultado será una matriz con el mismo número de filas que la primera matriz y el mismo número de columnas que la segunda matriz. El elemento de la matriz producto situado en la fila  y columna
y columna  será el “producto escalar” (entendido como suma de productos de componentes correspondientes) del
será el “producto escalar” (entendido como suma de productos de componentes correspondientes) del  -ésimo “vector fila” de la primera matriz por el
-ésimo “vector fila” de la primera matriz por el  -ésimo “vector columna” de la segunda matriz: en la figura se ha señalado como se obtiene la segunda componente del vector columna
-ésimo “vector columna” de la segunda matriz: en la figura se ha señalado como se obtiene la segunda componente del vector columna  como producto de la segunda fila de la matriz
como producto de la segunda fila de la matriz  por el vector columna
por el vector columna  . También se visualiza matricialmente cómo la vector imagen del vector columna
. También se visualiza matricialmente cómo la vector imagen del vector columna  no es más que el
no es más que el  -ésimo vector columna de la matriz
-ésimo vector columna de la matriz  .
.
Una matriz  cualquiera estará asociada a una transformación lineal. Pero ahora sólo queremos considerar específicamente las rotaciones entre las transformaciones lineales, y por tanto tenemos que ver qué matrices describen una rotación. En primer lugar, las rotaciones conservan las longitudes, mantienen la norma de los vectores rotados. Concretamente, las columnas de la matriz
cualquiera estará asociada a una transformación lineal. Pero ahora sólo queremos considerar específicamente las rotaciones entre las transformaciones lineales, y por tanto tenemos que ver qué matrices describen una rotación. En primer lugar, las rotaciones conservan las longitudes, mantienen la norma de los vectores rotados. Concretamente, las columnas de la matriz  que describe una rotación
que describe una rotación  representan los vectores ya rotados de la base ortonormal de partida, tal como se muestra en la siguiente figura:
representan los vectores ya rotados de la base ortonormal de partida, tal como se muestra en la siguiente figura:

Pero como  no es una matriz asociada a una transformación lineal cualquiera, sino que representa una rotación, debe cumplir ciertas condiciones extra. Para empezar, los vectores que resultan de rotar los vectores de la base ortonormal deben formar también a su vez una base ortonormal. Así que estos vectores deben estar normalizados, y deben cumplir
no es una matriz asociada a una transformación lineal cualquiera, sino que representa una rotación, debe cumplir ciertas condiciones extra. Para empezar, los vectores que resultan de rotar los vectores de la base ortonormal deben formar también a su vez una base ortonormal. Así que estos vectores deben estar normalizados, y deben cumplir  . En lenguaje matricial el producto interior de vectores se expresa mediante el producto del vector transpuesto (“vector fila”) por un vector (“vector columna”) sin transponer, de modo que escribiremos:
. En lenguaje matricial el producto interior de vectores se expresa mediante el producto del vector transpuesto (“vector fila”) por un vector (“vector columna”) sin transponer, de modo que escribiremos:
![\\mathsf{e^\\prime}_1^\\mathsf{T} \\mathsf{e^\\prime}_1 = \\left[ \\begin{array}{ccc} r_{11} \\& r_{21} \\& r_{31} \\end{array}\\right] \\left[ \\begin{array}{c} r_{11} \\ r_{21} \\r_{31} \\end{array}\\right] = 1](http://eltamiz.com/elcedazo/wp-content/uploads/2020/01/tex80_36c0fffc1db43bc9ac7df77db86da51a.png)
![\\mathsf{e^\\prime}_2^\\mathsf{T} \\mathsf{e^\\prime}_2 = \\left[ \\begin{array}{ccc} r_{12} \\& r_{22} \\& r_{32} \\end{array}\\right] \\left[ \\begin{array}{c} r_{12} \\ r_{22} \\r_{32} \\end{array}\\right] = 1](http://eltamiz.com/elcedazo/wp-content/uploads/2020/01/tex80_78365ebf340557f0e78eb7d0bd632a21.png)
![\\mathsf{e^\\prime}_3^\\mathsf{T} \\mathsf{e^\\prime}_3 = \\left[ \\begin{array}{ccc} r_{13} \\& r_{23} \\& r_{33} \\end{array}\\right] \\left[ \\begin{array}{c} r_{13} \\ r_{23} \\r_{33} \\end{array}\\right] = 1](http://eltamiz.com/elcedazo/wp-content/uploads/2020/01/tex80_d7c885825ac71720531214123bacdacb.png)
Además, dos vectores diferentes de la base rotada deben ser ortogonales entre sí, y se deberá cumplir también que:
 , cuando
, cuando  .
.
Lo que matricialmente se expresaría así:
![\\mathsf{e^\\prime}_i^\\mathsf{T} \\mathsf{e^\\prime}_j = \\left[ \\begin{array}{ccc} r_{1i} \\& r_{2i} \\& r_{3i} \\end{array}\\right] \\left[ \\begin{array}{c} r_{1j} \\ r_{2j} \\r_{3j} \\end{array} \\right] = 0](http://eltamiz.com/elcedazo/wp-content/uploads/2020/01/tex80_0d06ddb37c422eb5412df86cf10a454e.png) , cuando
, cuando  .
.
Pero resulta que todas estas condiciones de normalización y ortogonalidad se pueden expresar como una única identidad matricial, que no es más que  , donde
, donde  es la matriz transpuesta de
es la matriz transpuesta de  , o sea, el resultado de cambiar filas por columnas, y
, o sea, el resultado de cambiar filas por columnas, y  es la matriz identidad, es decir, aquella matriz que tiene unos en la diagonal principal (cuando el índice de fila y el de columna son iguales) y ceros en el resto de posiciones:
es la matriz identidad, es decir, aquella matriz que tiene unos en la diagonal principal (cuando el índice de fila y el de columna son iguales) y ceros en el resto de posiciones:
![\\mathsf{R^T} \\mathsf{R} = \\left[ \\begin{array}{ccc} r_{11} & r_{21} & r_{31} \\\\ r_{12} & r_{22} & r_{32} \\\\ r_{31} & r_{32} & r_{33} \\end{array} \\right] \\left[ \\begin{array}{ccc} r_{11} & r_{12} & r_{13} \\\\ r_{12} & r_{22} & r_{23} \\\\ r_{13} & r_{23} & r_{33} \\end{array} \\right] = \\left[ \\begin{array}{ccc} 1 & 0 & 0 \\\\ 0 & 1 & 0 \\\\ 0 & 0 & 1 \\end{array} \\right] = \\mathbb{1}](http://eltamiz.com/elcedazo/wp-content/uploads/2020/02/tex80_e0b4e6a12ab9f7f9fb46b68323f405a6.png)
Efectivamente, el elemento situado en la fila  y columna
y columna  del resultado del producto de matrices no es más que el producto interior del vector
del resultado del producto de matrices no es más que el producto interior del vector 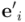 , que está codificado en la fila
, que está codificado en la fila  de la matriz
de la matriz  , por el vector
, por el vector  , codificado en la columna
, codificado en la columna  de la segunda matriz. Resulta, pues, que la identidad
de la segunda matriz. Resulta, pues, que la identidad  no nos está diciendo otra cosa más que en una matriz de rotación los vectores columna forman una base ortonormal, ya que la tabla de productos escalares
no nos está diciendo otra cosa más que en una matriz de rotación los vectores columna forman una base ortonormal, ya que la tabla de productos escalares  es precisamente la matriz identidad. El conjunto formado por todas las matrices
es precisamente la matriz identidad. El conjunto formado por todas las matrices  de tres filas y tres columnas que cumplen
de tres filas y tres columnas que cumplen  se llama
se llama  , el llamado grupo ortogonal de 3 dimensiones.[1]
, el llamado grupo ortogonal de 3 dimensiones.[1]
Pero no toda matriz de  es una matriz de rotación. Dentro de
es una matriz de rotación. Dentro de  hay también matrices que representan reflexiones, las transformaciones que, dicho coloquialmente, transforman una mano izquierda en una mano derecha, algo imposible de conseguir haciendo rotaciones. Para excluir las reflexiones hay que introducir una condición más: la orientación de la base ortonormal rotada tiene que ser la misma que la de la base antes de la rotación. Esta condición se puede expresar con el producto exterior de vectores:
hay también matrices que representan reflexiones, las transformaciones que, dicho coloquialmente, transforman una mano izquierda en una mano derecha, algo imposible de conseguir haciendo rotaciones. Para excluir las reflexiones hay que introducir una condición más: la orientación de la base ortonormal rotada tiene que ser la misma que la de la base antes de la rotación. Esta condición se puede expresar con el producto exterior de vectores:
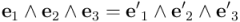
La igualdad anterior expresa que el volumen orientado del cubo que tiene por aristas los vectores de la base ortonormal es el mismo antes que después de la rotación, sin cambios de signo debidos a cambios de orientación.[2] Si expresamos los vectores de la base rotada en términos de la base antigua llegamos a esta expresión para  :
:



Al desarrollar el producto exterior acaba apareciendo multiplicando al trivector un factor, señalado en verde, conocido como determinante de la matriz  . El determinante indica por cuánto se multiplica el volumen del pseudoescalar unitario
. El determinante indica por cuánto se multiplica el volumen del pseudoescalar unitario  tras la transformación lineal, indicando un signo negativo un cambio de orientación respecto a la base de partida. Para las matrices de
tras la transformación lineal, indicando un signo negativo un cambio de orientación respecto a la base de partida. Para las matrices de  el valor del determinante sólo puede ser +1 o -1, pero si ademas queremos que la matriz represente una rotación el determinante sólo puede valer +1. El subconjunto de matrices de
el valor del determinante sólo puede ser +1 o -1, pero si ademas queremos que la matriz represente una rotación el determinante sólo puede valer +1. El subconjunto de matrices de  cuyo determinante vale +1, con la operación de producto matricial, forman el grupo
cuyo determinante vale +1, con la operación de producto matricial, forman el grupo  , que sí representa el grupo de rotaciones en el espacio euclídeo tridimensional.[3]
, que sí representa el grupo de rotaciones en el espacio euclídeo tridimensional.[3]
Rotores (cuaterniones unitarios) versus matrices: eficiencia de cálculo
Por tanto, podemos representar rotaciones en el espacio tridimensional utilizando matrices de  , como hemos visto en esta entrada, o, como vimos en la entrada pasada, las podemos representar utilizando cuaterniones unitarios (exponenciales de bivectores unitarios). Y aquí se plantea cuál de los dos métodos es más práctico. Imaginemos el programador de un videojuego en que se visualicen escenas realistas en 3D o de un simulador de vuelo en tiempo real: esta cuestión deberá tenerla muy en cuenta.
, como hemos visto en esta entrada, o, como vimos en la entrada pasada, las podemos representar utilizando cuaterniones unitarios (exponenciales de bivectores unitarios). Y aquí se plantea cuál de los dos métodos es más práctico. Imaginemos el programador de un videojuego en que se visualicen escenas realistas en 3D o de un simulador de vuelo en tiempo real: esta cuestión deberá tenerla muy en cuenta.
Para hallar la rotación resultante,  ,de componer dos rotaciones, la primera
,de componer dos rotaciones, la primera  , seguida de una segunda
, seguida de una segunda  ,
,  , utilizando matrices de
, utilizando matrices de  tendremos que multiplicar dos matrices de tres filas y tres columnas:
tendremos que multiplicar dos matrices de tres filas y tres columnas:  . Esto requiere hacer 3 multiplicaciones para obtener cada uno de los 9 elementos de la matriz correspondiente a la rotación resultante final, en total, 27 multiplicaciones. Las multiplicaciones son computacionalmente mucho más costosas que las sumas, que no tenemos en cuenta (y, por cierto, también el número de sumas a realizar en el caso del producto de matrices supera al necesario en el caso del producto de cuaterniones).
. Esto requiere hacer 3 multiplicaciones para obtener cada uno de los 9 elementos de la matriz correspondiente a la rotación resultante final, en total, 27 multiplicaciones. Las multiplicaciones son computacionalmente mucho más costosas que las sumas, que no tenemos en cuenta (y, por cierto, también el número de sumas a realizar en el caso del producto de matrices supera al necesario en el caso del producto de cuaterniones).
Si componemos rotaciones utilizando cuaterniones unitarios tendremos que multiplicar las cuatro componentes del primer rotor asociado a la primera rotación por las cuatro del segundo rotor, en total 16 multiplicaciones. Esto es computacionalmente mucho más eficiente que multiplicar matrices, pero los beneficios del uso de cuaterniones unitarios no acaban aquí…
Espacio de almacenamiento
En caso de que sea necesario almacenar rotaciones en disco o en memoria RAM, para almacenarlas en formato matricial hacen falta 9 números para cada una y para almacenarlas como cuaterniones sólo hacen falta cuatro (de hecho, “poco más de tres”, porque una componente de cuaternión se puede deducir de las otras tres por la condición de normalización, a excepción de un bit de signo que habría que tener también para que no faltara nada).
Acumulación de errores de redondeo
Cuando el programador del videojuego tenga que componer sucesivamente n rotaciones,  , seguida de
, seguida de  …
…  se irán acumulando inevitablemente errores de redondeo. Si utilizamos matrices de
se irán acumulando inevitablemente errores de redondeo. Si utilizamos matrices de  , estos errores harán que la matriz obtenida como resultado final,
, estos errores harán que la matriz obtenida como resultado final,  ya no cumpla la condición
ya no cumpla la condición  , debido a la acumulación de errores, y los vectores de la base ortonormal transformada, que aparecen representados en las columnas de la matriz
, debido a la acumulación de errores, y los vectores de la base ortonormal transformada, que aparecen representados en las columnas de la matriz  , ya no estarán bien normalizados, ni serán perfectamente perpendiculares entre sí, e incluso el volumen orientado que formen dejará de valer exactamente 1, y seguramente habrá aumentado o disminuido. Como esto no puede consentirse habrá que corregir la matriz obtenida antes de que el problema se desmadre, de modo que sus vectores columna estén perfectamente normalizados y sean perpendiculares entre sí. Hay un procedimiento muy conocido de lograr esto, llamado método de ortonormalización de Gram-Schmidt, que ya tendremos ocasión de ver en otra entrada. Pero tiene el problema de ser engorroso y poco elegante, porque obliga a elegir en un cierto orden, (normalizando primero uno de los vectores columna, a continuación restar de un segundo vector su proyección respecto al primero y normalizar el resultado a su vez, restar del tercer vector sus proyecciones respecto a los dos vectores normalizados obtenidos antes y normalizar el resultado, etc.) y la matriz corregida dependerá del orden en que se haya decidido normalizar los vectores, cosa que se notará tanto más cuanto más se haya dejado acumular los errores. En fin, el método de Gram-Schmidt sin más modificación resulta en sí mismo ser inestable computacionalmente: un auténtico horror para un programador que tenga que presentar una animación realista en tiempo real…
, ya no estarán bien normalizados, ni serán perfectamente perpendiculares entre sí, e incluso el volumen orientado que formen dejará de valer exactamente 1, y seguramente habrá aumentado o disminuido. Como esto no puede consentirse habrá que corregir la matriz obtenida antes de que el problema se desmadre, de modo que sus vectores columna estén perfectamente normalizados y sean perpendiculares entre sí. Hay un procedimiento muy conocido de lograr esto, llamado método de ortonormalización de Gram-Schmidt, que ya tendremos ocasión de ver en otra entrada. Pero tiene el problema de ser engorroso y poco elegante, porque obliga a elegir en un cierto orden, (normalizando primero uno de los vectores columna, a continuación restar de un segundo vector su proyección respecto al primero y normalizar el resultado a su vez, restar del tercer vector sus proyecciones respecto a los dos vectores normalizados obtenidos antes y normalizar el resultado, etc.) y la matriz corregida dependerá del orden en que se haya decidido normalizar los vectores, cosa que se notará tanto más cuanto más se haya dejado acumular los errores. En fin, el método de Gram-Schmidt sin más modificación resulta en sí mismo ser inestable computacionalmente: un auténtico horror para un programador que tenga que presentar una animación realista en tiempo real…
Interpolación de rotaciones
El uso de matrices de  tampoco es muy conveniente para la interpolación de rotaciones. Nuestro imaginario programador del videojuego, para representar un movimiento animado lo suficientemente suave, necesitará interpolar entre un estado inicial y un estado final de rotación, cada uno de ellos representado por una matriz de
tampoco es muy conveniente para la interpolación de rotaciones. Nuestro imaginario programador del videojuego, para representar un movimiento animado lo suficientemente suave, necesitará interpolar entre un estado inicial y un estado final de rotación, cada uno de ellos representado por una matriz de  . El problema es que si decide ingenuamente interpolar cada elemento
. El problema es que si decide ingenuamente interpolar cada elemento  de la matriz por separado obtendrá matrices que no serán ni por asomo de
de la matriz por separado obtendrá matrices que no serán ni por asomo de  . Lo que hace falta es tener el eje y el ángulo de rotación del objeto a rotar en el estado inicial, el eje y ángulo de rotación del objeto a rotar en el estado final e interpolar orientaciones de los ejes de rotación intermedios y valores del ángulo de rotación de forma adecuada, y luego traducirlo a lenguaje matricial. Pero, ¿cómo se visualiza en una matriz de
. Lo que hace falta es tener el eje y el ángulo de rotación del objeto a rotar en el estado inicial, el eje y ángulo de rotación del objeto a rotar en el estado final e interpolar orientaciones de los ejes de rotación intermedios y valores del ángulo de rotación de forma adecuada, y luego traducirlo a lenguaje matricial. Pero, ¿cómo se visualiza en una matriz de  el eje y ángulo
el eje y ángulo  de rotación? La teoría dice que la traza de una matriz de rotación (la suma de los valores de la diagonal principal de la matriz (
de rotación? La teoría dice que la traza de una matriz de rotación (la suma de los valores de la diagonal principal de la matriz ( ) vale
) vale  , lo que permite calcular el coseno del ángulo, y a partir de ahí su valor absoluto (el signo, asociado al sentido de rotación, queda indeterminado, con lo que queda pendiente el trabajo de deducirlo aparte). En cuanto a “visualizar” el eje de rotación en una matriz de
, lo que permite calcular el coseno del ángulo, y a partir de ahí su valor absoluto (el signo, asociado al sentido de rotación, queda indeterminado, con lo que queda pendiente el trabajo de deducirlo aparte). En cuanto a “visualizar” el eje de rotación en una matriz de  dada, hay que encontrar lo que en la jerga matemática se llama un autovector de la matriz con autovalor unidad, es decir, un vector que cumpla
dada, hay que encontrar lo que en la jerga matemática se llama un autovector de la matriz con autovalor unidad, es decir, un vector que cumpla 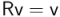 , que en principio no es algo que se pueda decir que salte a la vista… Se trata de encontrar un vector normalizado que da la solución a un sistema de ecuaciones indeterminado.
, que en principio no es algo que se pueda decir que salte a la vista… Se trata de encontrar un vector normalizado que da la solución a un sistema de ecuaciones indeterminado.
En cambio, estos problemas se solucionan muy fácilmente con cuaterniones unitarios. El problema de la acumulación de errores se arregla de forma inmediata normalizando el cuaternión obtenido como resultado del producto de cuaterniones: dividiendo el cuaternión entre su módulo volvemos a tener un cuaternión unitario que vuelve a representar automáticamente una rotación, y en la animación veremos cómo el objeto animado va rotando sin crecer ni encogerse como resultado de la acumulación de errores (al usar cuaterniones en vez de matrices, el único tipo de distorsión que puede aparecer si no nos preocupamos de la normalización son cambios uniformes de escala, quedando excluidas de antemano escalas diferentes de distorsión según la dirección). El tratamiento de la acumulación de errores es incomparablemente más sencillo usando cuaterniones unitarios.
El problema de la interpolación entre diferentes estados de rotación es muy sencillo, porque en un rotor  es inmediato reconocer el eje y ángulo (con su correspondiente sentido expresado de forma inambigua) de rotación:
es inmediato reconocer el eje y ángulo (con su correspondiente sentido expresado de forma inambigua) de rotación:
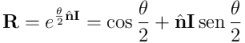
Simplemente se identifica la parte real del rotor con  . Suponiendo que
. Suponiendo que  (que correspondería, no importa el signo, al caso de una transformación identidad),[4] tendremos que la parte bivectorial será no nula, y se podrá identificar con el bivector que da el plano de rotación. La norma de este bivector se puede identificar con el seno del semiángulo de rotación, y el sentido de rotación queda determinado de forma no ambigua: no importa cómo se elija el signo del ángulo, el sentido de rotación queda siempre expresado por el sentido del vector unitario
(que correspondería, no importa el signo, al caso de una transformación identidad),[4] tendremos que la parte bivectorial será no nula, y se podrá identificar con el bivector que da el plano de rotación. La norma de este bivector se puede identificar con el seno del semiángulo de rotación, y el sentido de rotación queda determinado de forma no ambigua: no importa cómo se elija el signo del ángulo, el sentido de rotación queda siempre expresado por el sentido del vector unitario  , que cambiará acordemente con la elección del signo para seguir la regla de la mano derecha (suponiendo que hemos elegido la orientación derecha para el pseudoescalar unitario estándar
, que cambiará acordemente con la elección del signo para seguir la regla de la mano derecha (suponiendo que hemos elegido la orientación derecha para el pseudoescalar unitario estándar  ):
):
Sólo hay un aspecto en que el uso de matrices es superior al de cuaterniones en el tratamiento de rotaciones en 3D. Se trata, una vez se tiene la rotación deseada perfectamente calculada, de aplicarla a una serie de vectores, por ejemplo para obtener una escena tridimensional rotada. Matricialmente, se trata hacer el producto de la matriz de rotación por el vector columna:  . Eso supone hacer 9 multiplicaciones: cada una de las tres componentes del vector rotado se obtiene como producto interior (suma de tres multiplicaciones) de cada vector fila de
. Eso supone hacer 9 multiplicaciones: cada una de las tres componentes del vector rotado se obtiene como producto interior (suma de tres multiplicaciones) de cada vector fila de  por el vector original. Con álgebra geométrica hay que calcular, como ya vimos en la entrada pasada, el sandwich multiplicativo siguiente:
por el vector original. Con álgebra geométrica hay que calcular, como ya vimos en la entrada pasada, el sandwich multiplicativo siguiente:  , donde
, donde  es el rotor (cuaternión unitario) asociado a la rotación
es el rotor (cuaternión unitario) asociado a la rotación  . Operando astutamente, eso aún se puede reducir a hacer 15 multiplicaciones, lo cual no es suficiente para competir con las matrices. Así que más vale, una vez tenemos el rotor
. Operando astutamente, eso aún se puede reducir a hacer 15 multiplicaciones, lo cual no es suficiente para competir con las matrices. Así que más vale, una vez tenemos el rotor  , calcular la matriz
, calcular la matriz encontrando las imágenes de los vectores de la base ortonormal estándar, y una vez ahí, se calcula matricialmente la rotación de todos los vectores que haga falta. Sólo en este aspecto concreto, la rotación de vectores, la superioridad del método matricial es indiscutible.
encontrando las imágenes de los vectores de la base ortonormal estándar, y una vez ahí, se calcula matricialmente la rotación de todos los vectores que haga falta. Sólo en este aspecto concreto, la rotación de vectores, la superioridad del método matricial es indiscutible.
Las ventajas del tratamiento de rotaciones con álgebra geométrica sobre la utilización de matrices se puso de manifiesto de forma práctica en la segunda mitad de la década de los 90, cuando apareció un videojuego que funcionaba en los primeros ordenadores con procesador Intel Pentium y compatibles (y a diferencia de otros juegos 3D de aquella época que todavía no utilizaban cuaterniones, también incluso en procesadores 486, de la generación anterior). Gracias al uso de cuaterniones fue posible exprimir al máximo las capacidades de aquellos primitivos procesadores y mostrar las aventuras de una ágil y atractiva arqueóloga que no paraba de dar volteretas y giros rapidísimos mientras se movía en un mundo totalmente tridimensional, respondiendo inmediatamente a los comandos de los jugadores, que hasta entonces no habían visto nada igual en aquellos ordenadores, mucho más lentos que los de hoy en día (ya habían aparecido otros juegos de aventuras en 3D, pero como no usaban cuaterniones no podían competir con éste por lo que se refiere a la rapidez, eficiencia y realismo en el tratamiento de las rotaciones).
En la próxima entrada veremos en más detalle que el modo en que las rotaciones se representan en  y el modo en que se representan con rotores (o cuaterniones unitarios, o espinores unitarios de
y el modo en que se representan con rotores (o cuaterniones unitarios, o espinores unitarios de  , como queráis decir) no son completamente equivalentes, qué hay detrás de eso y qué relación puede tener, por ejemplo, con la Física o con la robótica.
, como queráis decir) no son completamente equivalentes, qué hay detrás de eso y qué relación puede tener, por ejemplo, con la Física o con la robótica.
-
En los libros de texto la deducción de que la matriz inversa de la matriz asociada a una transformación isométrica es la matriz transpuesta se suele hacer de forma más expeditiva y elegante. Como el producto escalar de vectores determina la métrica (cómo se miden las longitudes y ángulos), tiene que conservarse en una transformación isométrica, es decir, para cualquier par de vectores
 y
y 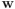 , el producto escalar
, el producto escalar  debe conservarse y ser por tanto igual a
debe conservarse y ser por tanto igual a  , donde
, donde  y
y 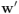 son los respectivos vectores transformados. Pero matricialmente esto se escribe:
son los respectivos vectores transformados. Pero matricialmente esto se escribe:
Y de ahí se deduce que si la igualdad es cierta para cualquier par de matrices columna
 y
y  , debe cumplirse
, debe cumplirse  . [↩]
. [↩] -
Si la transformación fuera una reflexión se introduciría una cambio de signo en el fórmula:
 . [↩]
. [↩] -
La S de
 viene de special, por incluir sólo las matrices de determinante igual a +1. En el grupo ortogonal
viene de special, por incluir sólo las matrices de determinante igual a +1. En el grupo ortogonal  hay tanto matrices de determinante +1 como -1. En
hay tanto matrices de determinante +1 como -1. En  , todas las matrices tienen determinante +1. [↩]
, todas las matrices tienen determinante +1. [↩] -
Lo que vemos aquí es que el mismo rotor cambiado de signo representa la misma rotación. Efectivamente, si para rotar un multivector cualquiera hacemos
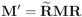 , un cambio de signo de
, un cambio de signo de 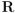 implica también el cambio de signo de
implica también el cambio de signo de  , y por tanto se obtiene el mismo resultado para
, y por tanto se obtiene el mismo resultado para 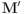 . El hecho de que una misma rotación esté representada por dos rotores, a diferencia de las matrices de
. El hecho de que una misma rotación esté representada por dos rotores, a diferencia de las matrices de  , en que una rotación está representada por solamente una matriz, será especialmente importante en la próxima entrada. [↩]
, en que una rotación está representada por solamente una matriz, será especialmente importante en la próxima entrada. [↩]

The Explorando el álgebra geométrica 17 – Rotaciones en el espacio euclídeo tridimensional (II) by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.





Escribe un comentario