Explorando el álgebra geométrica 16 – Rotaciones en el espacio euclídeo tridimensional (I)

En esta nueva entrada de la serie dedicada al álgebra geométrica veremos las rotaciones en el espacio euclídeo tridimensional. Como vimos en la entrada anterior, todas las rotaciones en este espacio son simples. De ahí resulta que todos los operadores de rotación, o rotores, del álgebra $\mathcal{G}_3$ se pueden expresar como cuaterniones unitarios. Componer rotaciones en tres dimensiones viene a ser multiplicar cuaterniones unitarios. Reconocer en esos cuaterniones unitarios los ángulos y ejes de rotación es muy sencillo. De hecho, el uso de cuaterniones es el método más simple de obtener el ángulo y el eje resultante de la composición de rotaciones en tres dimensiones.

En la pasada entrada ya vimos que todas las rotaciones en el espacio de tres dimensiones son simples, es decir, afectan a la proyección de los vectores sobre un subespacio bidimensional, mientras dejan sin modificar la exclusión de los vectores respecto a ese subespacio, que no queda afectada. El correspondiente operador de rotación, o rotor, correspondiente a una rotación simple de ángulo $\theta$ y de orientación dada por el bivector unitario $\hat{\mathbf{B}}$ , es, como vimos:

$\mathbf{R} = e^{\frac{\theta}{2}\hat{\mathbf{B}}}$

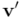También vimos que a partir de un vector $\mathbf{v}$ podíamos obtener el correspondiente vector rotado, $\mathbf{v^\prime}$ , del siguiente modo:

$\\mathbf{v^\\prime} = \\mathcal{R}\\left(\\mathbf{v}\\right) = \\widetilde{\\mathbf{R}} \\mathbf{v} \\mathbf{R} = e^{-\\frac{\\theta}{2}\\hat{\\mathbf{B}}} \\mathbf{v} e^{\\frac{\\theta}{2}\\hat{\\mathbf{B}}}$

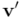Donde $\mathcal{R}$ designa propiamente a la rotación que convierte el objeto (en este caso, vector) $\mathbf{v}$ en su versión rotada, $\mathbf{v^\prime}$ , siendo $\mathbf{R}$ el operador o rotor asociado a la rotación $\mathcal{R}$ .

Rotación de un multivector cualquiera

Si hay que rotar un multivector $\mathbf{M}$ cualquiera, basta recordar que siempre podemos expresarlo como sumas de multivectores de grado homogéneo, y a su vez cada uno de esos multivectores homogéneos se pueden expresar como productos geométricos de vectores (que pueden ser perfectamente los de la base canónica ortonormal). Por ejemplo, si tenemos este multivector:

$\mathbf{M} = 5 - 3 \mathbf{e}_1 + 2 \mathbf{e}_1 \mathbf{e}_2 + 4 \mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_3$

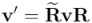El multivector rotado, $\mathbf{M^\prime}$ , será el que resulte de aplicar la rotación a cada vector que forme parte de la expresión. Por tanto, si para obtener la rotación de un vector $\mathbf{v}$ hacemos $\mathbf{v^\prime} = \widetilde{\mathbf{R}} \mathbf{v} \mathbf{R}$ , obtendremos la rotación del multivector $\mathbf{M}$ haciendo:

$\mathbf{M^\prime} = 5 - 3 \widetilde{\mathbf{R}} \mathbf{e}_1 \mathbf{R} + 2 \widetilde{\mathbf{R}} \mathbf{e}_1 \mathbf{R} \widetilde{\mathbf{R}} \mathbf{e}_2 \mathbf{R} + 4 \widetilde{\mathbf{R}} \mathbf{e}_1 \mathbf{R} \widetilde{\mathbf{R}} \mathbf{e}_2 \mathbf{R} \widetilde{\mathbf{R}} \mathbf{e}_3 \mathbf{R} =$

Pero ahora, como resulta que, como ya vimos en la entrada anterior, 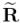$\widetilde{\mathbf{R}}$ es el inverso de $\mathbf{R}$ , tenemos no sólo que $\widetilde{\mathbf{R}} \mathbf{R} = 1$ , sino también $\mathbf{R} \widetilde{\mathbf{R}} =1$ . Por tanto, la expresión para la rotación del multivector se simplificará y tendremos:

$\mathbf{M^\prime} = 5 - 3 \widetilde{\mathbf{R}} \mathbf{e}_1 \mathbf{R} + 2 \widetilde{\mathbf{R}} \mathbf{e}_1 \mathbf{e}_2 \mathbf{R} + 4 \widetilde{\mathbf{R}} \mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_3 \mathbf{R} =$

Y ahora podemos escribir todo sacando 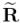$\widetilde{\mathbf{R}}$ como factor común por la izquierda, y $\mathbf{R}$ como factor común por la derecha:

$\mathbf{M^\prime} = \widetilde{\mathbf{R}} \left(5 - 3 \mathbf{e}_1 + 2 \mathbf{e}_1 \mathbf{e}_2 + 4 \mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_3\right) \mathbf{R} = \widetilde{\mathbf{R}} \mathbf{M} \mathbf{R}$

Fijémonos la expresión que hemos obtenido finalmente:

$\\mathbf{M^\prime} = \\mathcal{R}\\left(\\mathbf{M}\\right) = \\widetilde{\\mathbf{R}} \\mathbf{M} \\mathbf{R}$

Esta expresión que hemos obtenido para un multivector particular del álgebra geométrica asociada al espacio tridimensional euclídeo, $\mathcal{G}_3$ , tiene validez absolutamente general para cualquier multivector en cualquier álgebra geométrica, asociada a espacios de cualquier dimensión, euclídeos o pseudoeuclídeos: para rotar un multivector cualquiera basta multiplicarlo a su izquierda por la reversión del rotor correspondiente y a su derecha por el rotor sin revertir, exactamente igual que si fuera un vector.

Rotores en $\mathcal{G}_3$

Cualquier rotación en un espacio tridimensional es simple, y vimos que la expresión del rotor asociado a una rotación simple es 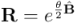$\mathbf{R} = e^{\frac{\theta}{2} \hat{\mathbf{B}}}$ , donde $\theta$ es el módulo del ángulo y el bivector unitario simple $\hat{\mathbf{B}}$ da la orientación y el plano (salvo paralelismos) de giro. Pero en tres dimensiones también podemos imaginar que las rotaciones son en torno a un eje, en vez de en un plano. Si preferimos dar la rotación con el ángulo y vector director del eje de rotación, basta utilizar el hecho de que en $\mathcal{G}_3$ se cumple $\mathbf{I}^2 = -1$ , donde $\mathbf{I}$ es el trivector unitario orientado canónico ( $\mathbf{I} = \mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_3$ ). Así, podremos expresar el rotor $\mathbf{R}$ :

$\mathbf{R} = e^{\frac{\theta}{2} \hat{\mathbf{B}}} = e^{\frac{\theta}{2} \hat{\mathbf{B}} \left(-\mathbf{I}\right) \mathbf{I}} = e^{\frac{\theta}{2} \hat{\mathbf{n}} \mathbf{I}}$

Donde $\hat{\mathbf{n}} = -\hat{\mathbf{B}} \mathbf{I}$ es el vector unitario que da la dirección del eje de rotación.

Una forma sencilla de comprobarlo sería expresar el bivector unitario $\hat{\mathbf{B}}$ como producto geométrico de dos vectores unitarios ortogonales entre sí: $\hat{\mathbf{B}} = \hat{\mathbf{f}}_1 \hat{\mathbf{f}}_2$ . 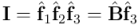El pseudoescalar canónico se puede escribir como producto de tres vectores unitarios ortogonales, de forma que los dos primeros sean respectivamente los $\hat{\mathbf{f}}_1$ y $\hat{\mathbf{f}}_2$ de antes: $\mathbf{I} = \hat{\mathbf{f}}_1 \hat{\mathbf{f}}_2 \hat{\mathbf{f}}_3 = \hat{\mathbf{B}} \hat{\mathbf{f}}_3$ . Por tanto, si multiplicamos ambos lados de la última igualdad por $\hat{\mathbf{B}}$ por la izquierda, tendremos:

$\hat{\mathbf{B}} \mathbf{I} = \hat{\mathbf{f}}_1 \hat{\mathbf{f}}_2 \hat{\mathbf{f}}_1 \hat{\mathbf{f}}_2 \hat{\mathbf{f}}_3 = -\hat{\mathbf{f}}_2 \hat{\mathbf{f}}_1 \hat{\mathbf{f}}_1 \hat{\mathbf{f}}_2 \hat{\mathbf{f}}_3 = -\hat{\mathbf{f}}_2 1 \hat{\mathbf{f}}_2 \hat{\mathbf{f}}_3 = -\hat{\mathbf{f}}_3$

Ahora basta reconocer que el vector unitario $\hat{\mathbf{f}}_3$ , por construcción perpendicular a la superficie orientada representada por el bivector simple y unitario $\hat{\mathbf{B}} = \hat{\mathbf{f}}_1 \hat{\mathbf{f}}_2$ , no es más que $\hat{\mathbf{n}}$ : $\hat{\mathbf{n}} = \hat{\mathbf{f}}_3$

Ya tenemos la expresión del rotor de $\mathcal{G}_3$ en función del ángulo y eje de rotación de rotación, que no es más que un multivector con términos de grado par que, recordemos, en $\mathcal{G}_3$ podemos equiparar a un cuaternión. Podemos decir que un rotor en $\mathcal{G}_3$ no es más que un cuaternión unitario (por cumplirse: $\widetilde{\mathbf{R}} \mathbf{R} = 1$ ).

Composición de dos rotaciones en $\mathcal{G}_3$

El resultado de aplicar a un multivector $\mathbf{M}$ en primer lugar una rotación $\mathcal{R}_1$ , seguida de una rotación $\mathcal{R}_2$ , cuyos respectivos rotores asociados sean $\mathbf{R}_1$ y $\mathbf{R}_2$ , será:

$\mathbf{M^\prime} = \mathcal{R}_2 \circ \mathcal{R}_1 \left(\mathbf{M}\right) = \mathcal{R}_2 \left(\mathcal{R}_1 \left(\mathbf{M} \right)\right) = \mathbf{\widetilde{R}}_2 \mathbf{\widetilde{R}}_1 \mathbf{M} \mathbf{R}_1 \mathbf{R}_2$

La notación $\circ$ indica simplemente la composición de funciones. En nuestro caso, la composición de las rotaciones $\mathcal{R}_2$ con $\mathcal{R}_1$ , lo cual permite referirnos a la rotación $\mathcal{R}$ como:

$\mathcal{R} = \mathcal{R}_2 \circ \mathcal{R}_1$

de modo que:

$\mathcal{R}\left(\mathbf{M}\right) = \mathcal{R}_2 \circ \mathcal{R}_1 \left(\mathbf{M}\right) = \mathcal{R}_2 \left(\mathcal{R}_1\left(\mathbf{M}\right)\right)$

La expresión para el multivector rotado permite identificar inmediatamente el rotor $\mathbf{R}$ , asociado a la rotación $\mathcal{R} = \mathcal{R}_2 \circ \mathcal{R}_1$ :

$\mathbf{R} = \mathbf{R}_1 \mathbf{R}_2$

La expresión es totalmente coherente con la propiedad de que la reversión de un producto de multivectores es el producto de las reversiones de los multivectores en orden invertido:

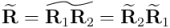
$\widetilde{\mathbf{R}} = \widetilde{\mathbf{R}_1 \mathbf{R}_2} = \widetilde{\mathbf{R}}_2} \widetilde{\mathbf{R}}_1$

Ejemplo: composición de dos rotaciones sucesivas en torno a dos ejes fijos en el espacio

Como muestra la siguiente figura, tenemos un dado en reposo sobre una superficie. Al principio vemos sus caras marcadas con uno, dos y tres puntos, y tomamos como vectores de nuestra base ortonormal los vectores $\mathbf{e}_1$ , $\mathbf{e}_2$ y $\mathbf{e}_3$ , que he representado precisamente como los vectores perpendiculares a las respectivas caras marcadas con uno, dos y tres puntos, y que apuntan hacia el exterior del dado. Hagamos una primera rotación de ángulo de $\phi = 90^\circ = \frac{\pi}{2} rad$ , en el el plano que contiene a los vectores $\mathbf{e}_1$ y $\mathbf{e}_2$ y con el sentido de rotación que va de $\mathbf{e}_1$ a $\mathbf{e}_2$ . Eso quiere decir que el rotor correspondiente será:

$\mathbf{R}_1 = e^{\frac{\phi}{2} \mathbf{e_1} \wedge \mathbf{e_2}} = e^{\frac{\pi}{4} \mathbf{e}_1 \mathbf{e}_2} = e^{\frac{\pi}{4} \mathbf{e}_3 \mathbf{I}}$

Partimos de un dado en la posición “1″ de la izquierda. Una rotación de $90^{\circ}$ ( $=\frac{\pi}{2}$ radianes) alrededor del eje cuyo vector director es ${\color{OliveGreen}{\mathbf{e}_3}}$ deja el dado en la posición “2″ de la derecha. El rotor asociado a la rotación es $\mathbf{R}_1 = e^{\mathbf{e}_1 \mathbf{e}_2 \frac{\pi}{4}$

En la figura de arriba podemos visualizar el efecto de la rotación, que tiene lugar en el plano de los vectores $\mathbf{e}_1$ y $\mathbf{e}_2$ , . En la posición final, etiquetada como “2″ en la figura, vemos que la cara del dado marcada con un punto pasa a ocupar la posición que al principio ocupaba la cara marcada con dos puntos, que a su vez pasa a ser la cara sobre la que reposa el dado, mientras que la cara marcada con tres puntos sigue teniendo como vector normal el vector $\mathbf{e}_3$ (los vectores de la base ortonormal de referencia, en verde, no los rotamos, sólo el dado).

En la figura siguiente partimos de la posición “2″ a la que se llegó tras la primera rotación y aplicamos una segunda rotación, también de 90º, pero esta vez en el plano de los ejes $\mathbf{e}_3$ y $\mathbf{e}_1$ y en el sentido que va de $\mathbf{e}_3$ a $\mathbf{e}_1$ . Como estamos en tres dimensiones, también podemos decir que hemos rotado en torno al eje $\mathbf{e}_2$ en el sentido dado por la regla de la mano derecha.^[1] Así, el dado acaba finalmente en la posición “3″.

Composición de rotaciones en tres dimensiones. Segunda rotación.

Tenemos el dado en la posición “2″ de la izquierda, en que lo hemos dejado antes. Una nueva rotación de $90^{\circ}$ ( $=\frac{\pi}{2}$ radianes) alrededor del eje cuyo vector director es ${\color{OliveGreen}{\mathb f{e}_2}}$ deja el dado en la posición “3″ de la derecha. El rotor asociado a esta segunda rotación es $\mathbf{R}_2 = e^{\mathbf{e}_3 \mathbf{e}_1 \frac{\pi}{4}}$ .

Bien, ahora podemos preguntarnos cuál es la rotación equivalente que lleva el dado directamente de la posición “1″ a la posición “3″. Sabemos que la rotación que buscamos, $\mathcal{R}$ tiene que ser el resultado de componer la segunda rotación, $\mathcal{R}_2$ , con la primera, $\mathcal{R}_1$ :

$\mathcal{R} = \mathcal{R}_2 \circ \mathcal{R}_1$

Y que el rotor $\mathbf{R}$ asociado a la rotación $\mathcal{R}$ será, por tanto:

$\mathbf{R} = \mathbf{R}_1 \mathbf{R}_2$

En el caso concreto de la rotación del dado, tenemos que:

$\mathbf{R}_1 = e^{\frac{\pi}{4} \mathbf{e}_1 \mathbf{e}_2}$

$\mathbf{R}_2 = e^{\frac{\pi}{4} \mathbf{e}_3 \mathbf{e}_1}$

Para encontrar $\mathbf{R}$ , habrá que multiplicar las dos expresiones anteriores que, al ser exponenciales de bivectores simples, podremos desarrollar en términos de cosenos y senos, como vimos en la entrada anterior. Además, en el caso tridimensional en que estamos, si recordamos lo dicho en la entrada 13, vemos que estas exponenciales “imaginarias” no son en el fondo más que cuaterniones unitarios:^[2]

$\mathbf{R} = \mathbf{R}_1 \mathbf{R}_2 = e^{\frac{\pi}{4} \mathbf{e}_1 \mathbf{e}_2} e^{\frac{\pi}{4} \mathbf{e}_3 \mathbf{e}_1} =$

$\left(\cos{\frac{\pi}{4} + \mathbf{e}_1 \mathbf{e}_2 \operatorname {{\textrm{sen}}} \frac{\pi}{4} \right) \left(\cos{\frac{\pi}{4} + \mathbf{e}_3 \mathbf{e}_1 \operatorname{{\textrm{sen}}} \frac{\pi}{4} \right) = \cos^2 \frac{\pi}{4} + \cos \frac{\pi}{4} \operatorname{{\textrm{sen}}} \frac{\pi}{4} \left(\mathbf{e}_3 \mathbf{e}_1 + \mathbf{e}_1 \mathbf{e}_2\right) + \mathbf{e}_2 \mathbf{e}_3 \operatorname{{\textrm{sen}}}^2 \frac{\pi}{4} =$

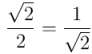Como tanto el coseno como el seno de $\frac{\pi}{4}$ radianes (= 45º) valen $\frac{\sqrt{2}}{2} = \frac{1}{\sqrt{2}}$ , si sustituimos el valor en la expresión anterior tendremos:

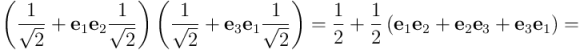
$\\left(\\frac{1}{\\sqrt{2}} + \\mathbf{e}_1 \\mathbf{e}_2 \\frac{1}{\\sqrt{2}} \\right) \\left(\\frac{1}{\\sqrt{2}} + \\mathbf{e}_3 \\mathbf{e}_1 \\frac{1} {\\sqrt{2}} \\right) = \\frac{1}{2} + \\frac{1}{2} \\left(\\mathbf{e}_1 \\mathbf{e}_2 + \\mathbf{e}_2 \\mathbf{e}_3 + \\mathbf{e}_3 \\mathbf{e}_1\\right) =$

Como además $\mathbf{I} \left(-\mathbf{I}\right) = 1$ , aprovecho para reexpresar el bivector como producto del pseudoescalar por un vector dual (el bivector da el sentido del plano de rotación, mientras que el vector dual, perpendicular al plano de la rotación, da el eje de rotación). Y así vamos arreglando la expresión, acercándonos a la forma deseada:

$\\frac{1}{2} + \\frac{1}{2} \\, \\mathbf{I} \\left(-\\mathbf{I}\\right) \\left(\\mathbf{e}_1 \\mathbf{e}_2 + \\mathbf{e}_2 \\mathbf{e}_3 + \\mathbf{e}_3 \\mathbf{e }_1\\right = \\frac{1}{2} + \\frac{1}{2} \\, \\mathbf{I} \\left(\\mathbf{e}_3 + \\mathbf{e}_1 + \\mathbf{e}_2\\right) =$

¿Y cuál es la forma deseada? Pues la forma estándar de expresar un rotor de $\mathcal{G}_3$ como exponencial del producto de un bivector unitario por un semiángulo, o sea, $e^{\\hat{\\mathbf{B}} \\frac{\\psi}{2}} = {\\color{BrickRed}\\cos \\frac{\\psi}{2}} + \\hat{\\mathbf{B}} \, {\\color{OliveGreen}\\operatorname {{\\textrm{sen}}} \\frac{\\psi}{2}}$ . Para eso aún nos queda normalizar el vector entre paréntesis, cuya norma vale $|\mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_3| = \sqrt{1^2+1^2+1^2} = \sqrt{3}$ . De esta forma el bivector unitario será $\\hat{\\mathbf{B}} = \\mathbf{I} \\, \\hat{\\mathbf{n}} = \\mathbf{I} \\, \\frac{\\mathbf{e}_1 + \\mathbf{e}_2 + \\mathbf{e}_3}{\\sqrt{3}}$ , donde asimismo identificamos el vector unitario $\hat{\mathbf{n}} = \frac{\mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_3}{\sqrt{3}}$ como el que da el eje de la rotación que buscamos:

${\color{RedBrick}\frac{1}{2}} + {\color{OliveGreen}\frac{\sqrt{3}}{2}} \, \mathbf{I} \\, \frac{\mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_3}{\sqrt{3}} = {\color{RedBrick}\cos \frac{\pi}{3}} + \mathbf{I} \, \frac{\mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_3}{\sqrt{3}} \\, {\color{OliveGreen}\operatorname{{\textrm{sen}}} \frac{\pi}{3}} = e^{\mathbf{I} \frac{\mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_3}{\sqrt{3}} \frac{\pi}{3}} = e^{\hat{\mathbf{B}} \frac{\psi}{2}} = \mathbf{R}$

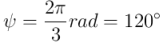El ángulo $\frac{\psi}{2}$ cuyo coseno vale $\frac{1}{2}$ y cuyo seno es positivo^[3] es el de 60º ( $= \frac{\pi}{3}$ radianes). De ahí deducimos que el valor del ángulo de la rotación es $\psi = \frac{2 \pi}{3} rad = 120^{\circ}$ .

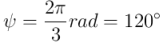Ya lo tenemos: hemos multiplicado dos cuaterniones unitarios, que eran los rotores $\mathbf{R}_1$ y $\mathbf{R}_2$ , y hemos obtenido otro cuaternión unitario, $\mathbf{R}$ , en el que podemos reconocer fácilmente el bivector unitario, $\hat{\mathbf{B}}$ , que da el plano y sentido de rotación, y el ángulo de rotación $\psi = \frac{2 \pi}{3} rad = 120^{\circ}$ . En lugar de usar el bivector $\hat{\mathbf{B}}$ como plano de rotación, podemos usar alternativamente el vector unitario $\hat{\mathbf{n}} = \frac{\mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_3}{\sqrt{3}}$ como eje de rotación, considerando positivo el sentido de rotación que sigue la regla de la mano derecha ya hemos elegido el pseudoescalar unitario siguiendo dicha regla. Si nos fijamos en las figuras, el vector unitario que da el eje de rotación es la normalización del vector que parte del origen de coordenadas, en el centro del dado, y apunta al vértice donde confluyen las tres caras visibles del dado. Y efectivamente, se puede comprobar que la rotación $\mathcal{R}$ resultante es una rotación de 120º positivos según la regla de la mano derecha en torno a eje dado por el vector $\hat{\mathbf{n}}$ . Veámoslo en la figura siguiente:

Rotación resultante de la composición de las dos rotaciones

La comparación de la posición “1″ original del dado con con su posición final, “3″, muestra que la rotación resultante $\mathcal{R} = \mathcal{R}_2 \circ \mathcal{R}_1$ es una rotación de 120º en torno al eje en que se encuentra el vector ${\color{RoyalBlue}\hat{\mathbf{n}}}$ , que en las imágenes del dado, debido a la perspectiva, apunta casi directamente al observador. El sentido positivo de rotación viene dado por la regla de la mano derecha.

Ejemplo del uso de la formula de rotación de un multivector

Veamos ahora un ejemplo de cómo rotar un multivector, en este caso el bivector ${\color{Red}\mathbf{e}_3 \wedge \mathbf{e}_1 = \mathbf{e}_3 \mathbf{e}_1}$ , que en la figura vemos que en la posición “1″ del dado aparece superpuesto a la cara del dado marcada con dos puntos:

En álgebra geométrica, para rotar cualquier tipo de multivector basta calcular el siguiente “sandwich” multiplicativo: la reversión del rotor asociado a la rotación por el objeto a rotar y por el rotor. En la figura, se ha ilustrado con el bivector dibujado sobre la cara del dado marcada con dos puntos: en la posición “1″ es el bivector 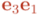${\color{BrickRed}\mathbf{e}_3 \mathbf{e}_1}$ , que tras la rotación pasa a ser el bivector ${\color{Orange}\mathbf{e}_1 \mathbf{e}_2}$ .

$\\mathcal{R} \\left({\\color{BricKRed}\\mathbf{e}_3 \\mathbf{e}_1}\\right) = \\widetilde{\\mathbf{R}} \, {\\color{Red}\\mathbf{e}_3 \\mathbf{e}_1} \\mathbf{R} = e^{-\\mathbf{I} {\\color{NavyBlue}\\frac{\\mathbf{e}_1 + \\mathbf{e}_2 + \\mathbf{e}_3}{\\sqrt{3}}} \\frac{\\pi}{3}} {\\color{Red}\\mathbf{e}_3 \\mathbf{e}_1} e^{\\mathbf{I} {\\color{NavyBlue}\\frac{\\mathbf{e}_1 + \\mathbf{e}_2 + \\mathbf{e}_3}{\\sqrt{3}}} \\frac{\\pi}{3}} =$

$\\left(\\cos \\frac{\\pi}{3} - \\mathbf{I} {\\color{NavyBlue}\\frac{\\mathbf{e}_1 + \\mathbf{e}_2 + \\mathbf{e}_3}{\\sqrt{3}}} \\operatorname{\\textrm{sen}} \\frac{\\pi}{3}\\right) {\\color{Red}\\mathbf{e}_3 \\mathbf{e}_1} \\left(\\cos \\frac{\\pi}{3} + \\mathbf{I} {\\color{NavyBlue}\\frac{\\mathbf{e}_1 + \\mathbf{e}_2 + \\mathbf{e}_3}{\\sqrt{3}}} \\operatorname{\\textrm{sen}} \\frac{\\pi}{3}\\right) = \\left(\\frac{1}{2} - \\mathbf{I} {\\color{NavyBlue}\\frac{\\mathbf{e}_1 + \\mathbf{e}_2 + \\mathbf{e}_3}{\\cancel{\\sqrt{3}}}} \\frac{\\cancel{\\sqrt{3}}}{2}\\right) {\\color{Red}\\mathbf{e}_3 \\mathbf{e}_1} \\left(\\frac{1}{2} + \\mathbf{I} {\\color{NavyBlue}\\frac{\\mathbf{e}_1 + \\mathbf{e}_2 + \\mathbf{e}_3}{\\cancel{\\sqrt{3}}}} \\frac{\\cancel{\\sqrt{3}}}{2}\\right) =$

$\left(\frac{1}{2} - \mathbf{I} \frac{\mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_3}{2}\right) {\color{BrickRed}\mathbf{e}_3 \mathbf{e}_1} \left(\frac{1}{2} + \mathbf{I} \frac{\mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_3}{2}\right) = \frac{1}{4} \mathbf{e}_3 \mathbf{e}_1 + \frac{1}{4} \mathbf{I} \left(\mathbf{e}_3 + \cancel{\mathbf{e}_3 \mathbf{e}_1 \mathbf{e}_2} - \mathbf{e}_1 \right) - \frac{1}{4} \mathbf{I} \left(-\mathbf{e}_3 + \cancel{\mathbf{e}_2 \mathbf{e}_3 \mathbf{e}_1} + \mathbf{e}_1\right) + \frac{1}{4} \left(-\mathbf{I} \mathbf{I}\right) \left(-\mathbf{e}_3 + \mathbf{e}_2 \mathbf{e}_3 \mathbf{e}_1 + \mathbf{e}_1 \right) \left(\mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_3\right) =$

En el cómputo de los productos cruzados he utilizado el hecho de que en $\mathcal{G}_3$ los pseudoescalares conmutan con los vectores y, por tanto, con cualquier multivector de $\mathcal{G}_3$ . Ahora queda aplicar que $\mathbf{I}^2 = -1$ y acabar de simplificar:

$\\frac{1}{4} \\mathbf{e}_3 \\mathbf{e}_1 + \\frac{1}{2} \\mathbf{I} \\left(\\mathbf{e}_3 - \\mathbf{e}_1 \\right) + \\frac{1}{4} \\left(-\\cancel{\\mathbf{e}_3 \\mathbf{e}_1} -\\mathbf{e}_3 \\mathbf{e}_2 - \\cancel{1} + \\mathbf{e}_2 \\mathbf{e}_3 + \\cancel{\\mathbf{e}_3 \\mathbf{e}_1} + \\mathbf{e}_1 \\mathbf{e}_2 + \\cancel{1} + \\mathbf{e}_1 \\mathbf{e}_2 + \\mathbf{e}_1 \\mathbf{e}_3 \\right) = \\frac{1}{4} \\mathbf{e}_3 \\mathbf{e}_1 + \\frac{1}{2} \\left(\\mathbf{e}_1 \\mathbf{e}_2 - \\mathbf{e}_2 \\mathbf{e}_3\\right) + \\frac{1}{4} \\left(2 \, \\mathbf{e}_2 \\mathbf{e}_3 + 2 \,\\mathbf{e}_1 \\mathbf{e}_2 + \\mathbf{e}_1 \\mathbf{e}_3\\right) =$

$\\cancel{\\frac{1}{4} \\mathbf{e}_3 \\mathbf{e}_1} + \\frac{1}{2} \\mathbf{e}_1 \\mathbf{e}_2 - \\bcancel{\\frac{1}{2} \\mathbf{e}_2 \\mathbf{e}_3} + \\bcancel{\\frac{1}{2} \\mathbf{e}_2 \\mathbf{e}_3} + \\frac{1}{2} \\mathbf{e}_1 \\mathbf{e}_2 + \\cancel{\\frac{1}{4} \\mathbf{e}_1 \\mathbf{e}_3} = {\\color{Orange}\\mathbf{e}_1 \\mathbf{e}_2}$

De igual modo se aplicaría el mismo procedimiento para rotar vectores. Por ejemplo, el vector normal a la cara marcada con un punto, que en la posición “1″ es $\mathbf{e}_1$ , tras la rotación pasaría a ser $\mathcal{R} \left(\mathbf{e}_1\right) = \widetilde{\mathbf{R}} \, \mathbf{e}_1 \mathbf{R}$ que daría como resultado el vector $\mathbf{e}_2$ . La fórmula de rotación para cualquier multivector $\mathbf{M}$ viene dada por el sandwich multiplicativo $\widetilde{\mathbf{R}} \mathbf{M} \mathbf{R}$ .

Visualización del eje y ángulo de rotación resultante de dos rotaciones mediante el uso de reflexiones

Hemos visto que el producto de dos rotores permite encontrar fácilmente el eje y ángulo de la rotación resultante de componer dos rotaciones. Como un rotor puede ser entendido como un cuaternión, eso quiere decir que la composición de dos rotaciones se puede representar por el producto de dos cuaterniones. El uso de cuaterniones sigue siendo el método más eficiente y elegante para representar rotaciones en el espacio euclídeo tridimensional. La Humanidad no dispuso de ninguna forma para calcular el eje y ángulo de la rotación resultante de componer dos rotaciones hasta el siglo XIX: aunque Euler, durante el siglo XVIII, ya había dado la expresión de las componentes de un vector que sufre una rotación de eje y ángulo dados, no dio ninguna expresión para el eje y ángulo de rotación resultante de la composición de dos rotaciones de ejes y ángulos de rotación dados. Esa expresión fue finalmente encontrada por Olinde Rodrigues (1795-1851) en 1840, quien se adelantó por muy poco al descubrimiento de los cuaterniones por Hamilton, en 1843. ¿Cómo dedujo Rodrigues su fórmula sin utilizar cuaterniones? No está claro cuál fue el origen de su inspiración, pero podría muy bien ser la idea de fabricar una rotación mediante la composición de dos reflexiones respecto a dos (hiper)planos, como vimos ya en la pasada entrada.

"Visualización del eje y ángulo de rotación resultante de componer dos rotaciones

Los vectores ${\color{Peach}\hat{\mathbf{n}}_1}$ y ${\color{Fuchsia}\hat{\mathbf{n}}_2}$ son, respectivamente, ejes de las rotaciones $\mathcal{R}_1$ y $\mathcal{R}_2$ , cuyos ángulos de rotación son, a su vez $\mathbf{\phi}$ y $\mathbf{\chi}$ . Tal como se explica en el texto que sigue, se construye un triángulo esférico de lados ${\color{OliveGreen}\mathsf{A}}$ , ${\color{Red}\mathsf{B}}$ y ${\color{Blue}\mathsf{C}}$ de modo que la rotación $\mathcal{R} = \mathcal{R}_2 \circ \mathcal{R}_1$ tiene por eje el vector ${\color{RoyalBlue}\hat{\mathbf{n}}}$ y por ángulo de rotación $\mathbf{\psi}$ , el doble del ángulo con que se cortan los planos que contienen los lados ${\color{OliveGreen}\mathsf{A}}$ y ${\color{Blue}\mathsf{C}}$ del triángulo esférico.

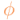Supongamos que queremos visualizar el resultado de componer dos rotaciones: la primera, $\mathcal{R}_1$ , de ángulo ${\color{Orange}\phi}$ y un eje que en la figura he representado en amarillo; y la segunda, $\mathcal{R}_2$ , de ángulo ${\color{Fuchsia}{\chi}$ y eje que en la figura he representado de color fucsia. Los ejes se cortan entre sí en el centro de una esfera, formando cierto ángulo entre ellos. Imaginemos el plano que contiene el punto de corte y los ejes de las rotaciones $\mathcal{R}_1$ y $\mathcal{R}_2$ : en la figura de abajo es el plano que pasa por el centro de la esfera y que la corta en una circunferencia máxima de la que vemos, en rojo, el arco ${\\color{Red}\\mathsf{B}}$ : llamaré a este plano $\mathbf{\pi_{B}}$ . Ahora construyamos dos planos más:

1) El primero, que llamaré $\mathbf{\pi_{A}}$ , será el plano que pasa por el centro de la esfera y se corta con el plano $\mathbf{\pi_{B}}$ de forma que el ángulo que va de $\mathbf{\pi_{A}}$ a $\mathbf{\pi_{B}}$ sea ${\color{Orange}\frac{\phi}{2}$ , o sea, la mitad del ángulo de la rotación $\mathcal{R}_1$ .

De este modo, podemos considerar la rotación $\mathcal{R}_1$ como la composición de dos reflexiones respecto a un plano: la primera respecto al plano $\mathbf{\pi_{A}}$ , seguida de la reflexión respecto al plano $\mathbf{\pi_{B}}$ . Como una reflexión es una simetría respecto a un plano, indicaré las reflexiones con la letra $\mathcal{S}$ , para diferenciarlas de las rotaciones:

$\mathcal{R}_1 = \mathcal{S}_{\pi_B} \circ \mathcal{S}_{\pi_A}$

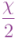2) El segundo plano, que llamaré $\mathbf{\pi_{C}}$ , será el plano que pasa por el centro de la esfera y se corta con el plano $\mathbf{\pi_{B}}$ de forma que el ángulo que va de $\mathbf{\pi_{B}}$ a $\mathbf{\pi_{C}}$ sea ${\color{Fuchsia}\frac{\chi}{2}}$ , o sea, también la mitad del ángulo de la rotación $\mathcal{R}_2$ .

De este modo, podemos considerar a la rotación $\mathcal{R}_2$ como la composición de dos reflexiones respecto a un plano: la primera respecto al plano $\mathbf{\pi_{B}}$ , seguida de la reflexión respecto al plano $\mathbf{\pi_{C}}$ :

$\mathcal{R}_2 = \mathcal{S}_{\pi_C} \circ \mathcal{S}_{\pi_B}$

La rotación $\mathcal{R}$ , equivalente a efectuar la rotación $\mathcal{R}_1$ seguida de la rotación $\mathcal{R}_2$ será, por tanto:

$\mathcal{R} = \mathcal{R}_2 \circ \mathcal{R}_1 = \left(\mathcal{S}_{\pi_C} \circ \mathcal{S}_{\pi_B}\right) \circ \left(\mathcal{S}_{\pi_B} \circ \mathcal{S}_{\pi_A}\right) = \mathcal{S}_{\pi_C} \circ \left(\mathcal{S}_{\pi_B} \circ \mathcal{S}_{\pi_B}\right) \circ \mathcal{S}_{\pi_A} =$

Donde se han suprimido los paréntesis, innecesarios debido a la propiedad asociativa de la composición de funciones. Pero, como vemos, aparece la composición de la reflexión $\mathcal{S}_{\pi_B}$ consigo misma, y una misma reflexión hecha dos veces consecutivas es lo mismo que no hacer nada (o sea, que tenemos $\mathcal{S}_{\pi_B} \circ \mathcal{S}_{\pi_B} = \mathcal{I}$ , donde $\mathcal{I}$ es la función identidad, el elemento neutro de la composición de movimientos). Así pues, tendremos que:

$\mathcal{R} = \mathcal{S}_{\pi_C} \circ \mathcal{I} \circ \mathcal{S}_{\pi_A} = \mathcal{S}_{\pi_C} \circ \mathcal{S}_{\pi_A}$

Es decir, hemos conseguido expresar el resultado de la composición de dos rotaciones como la composición de dos reflexiones respecto a dos planos, lo que es equivalente a una rotación cuyo eje es la recta en que se cortan los planos $\mathbf{\pi_{A}}$ y $\mathbf{\pi_{C}}$ (recta cuyo vector director en la figura está indicado como ${\color{NavyBlue}\hat{\mathbf{n}}}$ ). El ángulo de la rotación resultante, ${\color{NavyBlue}\psi}$ , es el doble del ángulo que va del plano $\mathbf{\pi_{A}}$ al plano $\mathbf{\pi_{C}}$ .^[4]

En la próxima entrada seguiremos con las rotaciones en el espacio euclídeo tridimensional. En concreto, hablaré de las ventajas y diferencias del método del álgebra geométrica, que utiliza cuaterniones, respecto al método clásico de las matrices ortogonales.

En álgebra geométrica, como el sentido de un bivector simple está determinado por el orden de los dos vectores que se multiplican exteriormente, la regla de la mano derecha es en el fondo superflua. En las figuras tridimensionales siempre escojo las bases ortonormales de modo que sigan la regla de la mano derecha (en este caso: 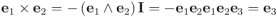$\mathbf{e}_1 \times \mathbf{e}_2 = -\left(\mathbf{e}_1 \wedge \mathbf{e}_2\right) \mathbf{I} = -\mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_3 = \mathbf{e}_3$ , donde he redefinido el producto vectorial de vectores en función del producto exterior y de la contracción con la unidad pseudoescalar, que he escogido, como se ve en la figura, respetando la regla de la mano derecha). Si no hablamos de rotaciones simples “en torno a un eje” sino “en un plano”, el uso de la regla de la mano derecha no es necesario. [↩]
Recordemos de la entrada 13 que podemos identificar bivectores unitarios de la base canónica $\mathbf{e}_1 \mathbf{e}_2$ , $\mathbf{e}_2 \mathbf{e}_3$ y $\mathbf{e}_1 \mathbf{e}_3$ con los cuaterniones $\mathbf{i}$ , $\mathbf{j}$ y $\mathbf{k}$ , respectivamente. De ahí resulta que los rotores de $\mathcal{G}_3$ , al ser exponenciales de bivectores simples (el análogo tridimensional de un número imaginario puro), se pueden considerar cuaterniones de módulo unidad, análogamente al modo en que una exponencial imaginaria es un número complejo unitario. [↩]
Dado el valor del coseno, el valor del seno está fijado, excepto en un signo, por la conocida fórmula 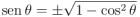$\operatorname{\textrm{sen}} \theta = \pm \sqrt{1 - \cos^2 \theta}$ . Como el coseno de nuestro ángulo $\frac{\psi}{2}$ vale $\frac{1}{2}$ , los valores posibles para el seno serían $\operatorname{\textrm{sen}} \frac{\psi}{2} = \pm \sqrt{1 - \left(\frac{1}{2}\right)^2} = \pm \sqrt{\frac{3}{4}} = \pm \frac{\sqrt{3}}{2}$ . Pero el valor negativo queda descartado al ver que el factor que está multiplicando a $\hat{\mathbf{B}}$ es el valor positivo. [↩]
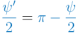En la figura he tomado el ángulo ${\color{NavyBlue}\frac{\psi}{2}}$ como ángulo exterior al triángulo esférico en el vértice. También lo podría haber tomado como el ángulo interior sin ningún problema, pero como también ha de ir de $\mathbf{\pi_{A}}$ a $\mathbf{\pi_{C}}$ , en este caso el ángulo interior es negativo, y valdría ${\\color{NavyBlue}\\frac{\\psi^{\\prime}}{2}} = {\\color{NavyBlue}\\pi - \\frac{\\psi}{2}}$ . A ello se correspondería un ángulo de rotación de 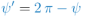${\color{NavyBlue}\psi^{\prime}} = {\color{NavyBlue} 2\,\pi - \psi}}$ , es decir, una vuelta completa de 360º menos el valor ${\color{NavyBlue}\psi}$ , que tiene el mismo efecto que rotar un ángulo ${\color{NavyBlue}\psi}$ . [↩]

The Explorando el álgebra geométrica 16 – Rotaciones en el espacio euclídeo tridimensional (I) by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.

El Cedazo

Explorando el álgebra geométrica 16 – Rotaciones en el espacio euclídeo tridimensional (I)

Sobre el autor:

jlese (Juan Leseduarte)

Escribe un comentario

Blog Search

Comentarios recientes

Spam bloqueado

Categorías

Documentación

Archivo