La serie dedicada al álgebra geométrica llega con esta entrada al importante tema de las rotaciones. En la entrada anterior vimos las simetrías axiales y las simetrías (reflexiones) respecto a un hiperplano. Veremos ahora cómo la composición de dos reflexiones (o, también, de dos simetrías axiales) resulta en una rotación simple.
La rotación simple como composición de dos reflexiones (o de dos simetrías axiales)
De la entrada anterior sabemos que el vector reflejado, o simetría respecto a un hiperplano ortogonal a un cierto vector  , de un vector
, de un vector  viene dada por esta expresión:
viene dada por esta expresión:

Donde 
Si al resultado de esta primera reflexión le aplicamos una segunda reflexión, esta vez respecto a otro hiperplano ortogonal a un vector  , obtendremos:
, obtendremos:

Como se puede ver, los dos signos negativos se neutralizan entre sí, y resulta finalmente que hacer dos reflexiones respecto a dos hiperplanos ortogonales a dos vectores  y
y  es lo mismo que hacer dos simetrías axiales, la primera respecto al eje dado por el vector
es lo mismo que hacer dos simetrías axiales, la primera respecto al eje dado por el vector  y la segunda respecto al eje dado por el vector
y la segunda respecto al eje dado por el vector  . Si al producto de vectores
. Si al producto de vectores  lo llamamos
lo llamamos  , vemos que el resultado de hacer dos simetrías axiales, que según vimos al final de la entrada anterior es una rotación, se puede expresar así:
, vemos que el resultado de hacer dos simetrías axiales, que según vimos al final de la entrada anterior es una rotación, se puede expresar así:

Donde el versor  es el producto geométrico
es el producto geométrico  , y
, y 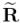 su correspondiente reversión.[1] Identificaremos
su correspondiente reversión.[1] Identificaremos  como el operador de la rotación o rotor resultante de componer las dos reflexiones, o alternativamente, las dos simetrías axiales.
como el operador de la rotación o rotor resultante de componer las dos reflexiones, o alternativamente, las dos simetrías axiales.
Observemos que 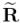 es el inverso de
es el inverso de  :
:

Además,  es la suma de un escalar y de un bivector:
es la suma de un escalar y de un bivector:

Como tanto  como
como  son vectores unitarios, tendremos que
son vectores unitarios, tendremos que  , donde
, donde  es el del ángulo que forman entre sí los dos vectores. Por otra parte, sabemos que el producto exterior
es el del ángulo que forman entre sí los dos vectores. Por otra parte, sabemos que el producto exterior 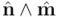 es una área orientada, cuya norma es:
es una área orientada, cuya norma es:

Entonces, suponiendo que  y
y  no son colineales, es posible definir un bivector simple y unitario, que llamaremos
no son colineales, es posible definir un bivector simple y unitario, que llamaremos  , de este modo:
, de este modo:

El bivector  , definido de esta forma, representa el mismo subespacio bidimensional que el bivector
, definido de esta forma, representa el mismo subespacio bidimensional que el bivector 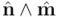 y tiene además su misma orientación.
y tiene además su misma orientación.
Y además, por ser  unitario, tendremos:
unitario, tendremos:

Es decir,  se comporta como una unidad imaginaria.
se comporta como una unidad imaginaria.
Tendremos así que  será igual a:
será igual a:

Para justificar la expresión como exponencial basta ir a la definición de la función exponencial para un multivector cualquiera  a partir de su desarrollo en serie:
a partir de su desarrollo en serie:

Y hagamos  :
:

Y aquí llega el momento de recordar que  se comporta como una unidad imaginaria y, por tanto, no sólo tenemos que
se comporta como una unidad imaginaria y, por tanto, no sólo tenemos que  , sino además
, sino además  ,
,  … análogamente al comportamiento de las potencias de la unidad imaginaria. Por tanto:
… análogamente al comportamiento de las potencias de la unidad imaginaria. Por tanto:

Ahora basta comparar los términos de grado par, que he marcado en verde, con el desarrollo en serie del coseno; y los términos de grado par, marcados en azul, con el desarrollo en serie del seno:


Y tras identificar los términos pares del desarrollo de la exponencial con los del desarrollo del coseno de  , y los términos impares del desarrollo de la exponencial con los del desarrollo del seno de
, y los términos impares del desarrollo de la exponencial con los del desarrollo del seno de  multiplicados por
multiplicados por  , se demuestra lo que no es más que una generalización de la fórmula de Euler que habíamos visto en la segunda entrada de esta serie:
, se demuestra lo que no es más que una generalización de la fórmula de Euler que habíamos visto en la segunda entrada de esta serie:

La deducción que en aquella entrada no hice, por no alargar, la he realizado finalmente aquí. Las buenas propiedades de convergencia de las series del seno y del coseno aseguran que esta forma de manipularlas es válida.
No es difícil ver que 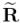 , como reversión de
, como reversión de  , tiene que ser:
, tiene que ser:
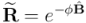
También conviene volver a insistir en que estos desarrollos en serie sólo son válidos si los ángulos están expresados en radianes (1 vuelta = 360º =  radianes).
radianes).
Veamos cuál es el resultado de aplicar a un vector  dos simetrías axiales. Vamos a considerar al vector
dos simetrías axiales. Vamos a considerar al vector  descompuesto en dos partes: una parte que llamaremos
descompuesto en dos partes: una parte que llamaremos 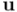 , ortogonal tanto al vector
, ortogonal tanto al vector  como al vector
como al vector  , o lo que es lo mismo, perpendicular a un plano que contenga al bivector
, o lo que es lo mismo, perpendicular a un plano que contenga al bivector 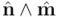 , y otra parte, que llamaremos
, y otra parte, que llamaremos  , que sea combinación lineal de los vectores
, que sea combinación lineal de los vectores  y
y  , o sea, que esté contenida en un plano que contenga al bivector
, o sea, que esté contenida en un plano que contenga al bivector 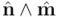 . En resumen:
. En resumen:

 (
(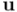 es ortogonal a
es ortogonal a  )
)
 (
(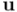 es ortogonal también a
es ortogonal también a  )
)
 (
( es combinación lineal de
es combinación lineal de  y
y  )
)
Así, el plan será ver cómo actúa la rotación sobre cada parte en que hemos descompuesto el vector  .
.
Más adelante, en esta misma entrada, veremos cómo el álgebra geométrica puede expresar y calcular cada una de estas dos partes en que descomponemos  .
.
Aplicar una rotación a una suma de vectores es lo mismo que sumar el resultado de las rotaciones de cada uno de los sumandos.[2].
Por tanto, podemos aplicar por separado la rotación a cada parte en que hemos descompuesto  :
:

Veamos primero qué le pasa a 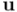 , la parte ortogonal a
, la parte ortogonal a  y
y  . Expresamos la rotación
. Expresamos la rotación  como producto de simetrías axiales:
como producto de simetrías axiales:

Como 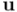 es ortogonal tanto a
es ortogonal tanto a  como a
como a  , los productos geométricos anticonmutan. El cambio de signo en el paréntesis central expresa que
, los productos geométricos anticonmutan. El cambio de signo en el paréntesis central expresa que 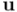 cambia de signo al sufrir la primera simetría axial respecto a un eje paralelo a
cambia de signo al sufrir la primera simetría axial respecto a un eje paralelo a  . Como hay un nuevo cambio de signo tras la segunda simetría axial, respecto a un eje paralelo a
. Como hay un nuevo cambio de signo tras la segunda simetría axial, respecto a un eje paralelo a  , finalmente resulta que cualquier vector ortogonal a los vectores
, finalmente resulta que cualquier vector ortogonal a los vectores  y
y  no resulta afectado tras las dos sucesivas simetrías axiales.
no resulta afectado tras las dos sucesivas simetrías axiales.
Pero veamos qué le sucede al vector  , que se encuentra en un plano paralelo al bivector simple
, que se encuentra en un plano paralelo al bivector simple 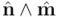 . En este subespacio bidimensional una simetría axial es lo mismo que una reflexión respecto al hiperplano (unidimensional) dado por el mismo eje de simetría, tal como vimos en la entrada anterior. En la figura siguiente podemos ver el efecto no sólo sobre un vector
. En este subespacio bidimensional una simetría axial es lo mismo que una reflexión respecto al hiperplano (unidimensional) dado por el mismo eje de simetría, tal como vimos en la entrada anterior. En la figura siguiente podemos ver el efecto no sólo sobre un vector  , sino, para apreciarlo mejor, sobre un par de vectores arbitrarios representados en rojo, y que llamaré
, sino, para apreciarlo mejor, sobre un par de vectores arbitrarios representados en rojo, y que llamaré  y
y 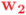 , que forman entre sí un ángulo
, que forman entre sí un ángulo  . Tras hacer la primera simetría de estos vectores respecto al eje dado por el vector unitario
. Tras hacer la primera simetría de estos vectores respecto al eje dado por el vector unitario  obtenemos respectivamente los vectores
obtenemos respectivamente los vectores  y
y  , representados en ocre en la figura. Aunque el módulo del ángulo que forman entre sí los vectores
, representados en ocre en la figura. Aunque el módulo del ángulo que forman entre sí los vectores  y
y  es idéntico al que formaban entre sí los vectores originales
es idéntico al que formaban entre sí los vectores originales  y
y 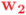 , el sentido ha cambiado, porque la simetría axial en dos dimensiones es un movimiento inverso que cambia el signo de los pseudoescalares relativos (o sea, los bivectores del subespacio bidimensional que estamos considerando). Una nueva simetría axial, esta vez respecto al eje dado por el vector unitario
, el sentido ha cambiado, porque la simetría axial en dos dimensiones es un movimiento inverso que cambia el signo de los pseudoescalares relativos (o sea, los bivectores del subespacio bidimensional que estamos considerando). Una nueva simetría axial, esta vez respecto al eje dado por el vector unitario  , transforma finalmente los vectores
, transforma finalmente los vectores  y
y  en
en  y
y  , respectivamente, representados en verde. Esta simetría axial introduce un nuevo cambio de signo de los pseudoescalares relativos al subespacio, de modo que el ángulo entre los vectores
, respectivamente, representados en verde. Esta simetría axial introduce un nuevo cambio de signo de los pseudoescalares relativos al subespacio, de modo que el ángulo entre los vectores  y
y  vuelve a tener el mismo módulo y sentido que el ángulo formado originalmente por
vuelve a tener el mismo módulo y sentido que el ángulo formado originalmente por  y
y 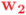 . El movimiento resultante de componer dos simetrías axiales es por tanto un movimiento directo, que no puede ser más que una rotación: si el módulo y sentido del ángulo relativo entre dos vectores se mantiene, el ángulo
. El movimiento resultante de componer dos simetrías axiales es por tanto un movimiento directo, que no puede ser más que una rotación: si el módulo y sentido del ángulo relativo entre dos vectores se mantiene, el ángulo  que ha rotado
que ha rotado  respecto a a
respecto a a  tiene que ser idéntico al que ha rotado
tiene que ser idéntico al que ha rotado  respecto a
respecto a 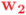 .
.

Podemos ver el efecto de la composición de dos simetrías axiales en el subespacio vectorial bidimensional generado por los vectores unitarios  y
y  . Partimos de dos vectores,
. Partimos de dos vectores,  y
y 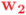 , indicados en rojo. En ocre se representan sus respectivos simétricos,
, indicados en rojo. En ocre se representan sus respectivos simétricos,  y
y  , respecto al eje dado por el vector unitario
, respecto al eje dado por el vector unitario  (todos los vectores se representan con un origen común). Una nueva simetría axial, esta vez respecto al eje dado por el vector unitario
(todos los vectores se representan con un origen común). Una nueva simetría axial, esta vez respecto al eje dado por el vector unitario  , transforma finalmente los vectores
, transforma finalmente los vectores  y
y  en
en  y
y  , respectivamente, representados en verde. Como esta simetría axial introduce un nuevo cambio de signo de los pseudoescalares relativos al subespacio, el ángulo entre los vectores
, respectivamente, representados en verde. Como esta simetría axial introduce un nuevo cambio de signo de los pseudoescalares relativos al subespacio, el ángulo entre los vectores  y
y  vuelve a ser
vuelve a ser  , con signo positivo. El movimiento resultante de componer dos simetrías axiales es, pues, un movimiento directo: una rotación. El ángulo de la rotación,
, con signo positivo. El movimiento resultante de componer dos simetrías axiales es, pues, un movimiento directo: una rotación. El ángulo de la rotación,  , resulta ser el doble del ángulo
, resulta ser el doble del ángulo  que va de
que va de  a
a  .
.
Para determinar el ángulo asociado a la rotación que resulta de componer dos simetrías axiales basta con ver cómo se transforma un vector cualquiera del subespacio bidimensional, por ejemplo, el vector  . Tras la primera simetría, respecto a sí mismo, este vector no cambia, naturalmente:
. Tras la primera simetría, respecto a sí mismo, este vector no cambia, naturalmente:

Y la segunda simetría, respecto a  , envía el vector
, envía el vector  a su posición definitiva que forma, respecto a la original, un ángulo que es el doble del que forma
a su posición definitiva que forma, respecto a la original, un ángulo que es el doble del que forma  con
con  , como se aprecia en la figura:
, como se aprecia en la figura:

El ángulo de la rotación que resulta de componer dos simetrías axiales es el doble del ángulo que forman entre sí los ejes de las simetrías, como se puede comprobar viendo a dónde envían las dos sucesivas simetrías al vector  , asociado a la primera simetría axial.
, asociado a la primera simetría axial.
El ángulo de la rotación,  , es, pues, el doble del ángulo
, es, pues, el doble del ángulo  que va de
que va de  a
a  . La composición de dos simetrías axiales es igual a una rotación en el plano que contiene los ejes de simetría y cuyo ángulo de rotación es el doble del ángulo que forman los ejes de simetría. El sentido de la rotación es el mismo que el del ángulo que va al primer eje de simetría al segundo.
. La composición de dos simetrías axiales es igual a una rotación en el plano que contiene los ejes de simetría y cuyo ángulo de rotación es el doble del ángulo que forman los ejes de simetría. El sentido de la rotación es el mismo que el del ángulo que va al primer eje de simetría al segundo.
Así pues, si queremos expresar el operador de una rotación simple en función del ángulo de rotación,  , y no del ángulo
, y no del ángulo  que forman entre sí los vectores
que forman entre sí los vectores  y
y  , hay que hacerlo así:
, hay que hacerlo así:

y para su reversión, 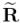 :
:

Proyección y exclusión de un vector respecto a un bivector simple. Primera extensión de los conceptos de producto interior y producto exterior.
Ahora toca ver cómo se expresa la descomposición de un vector cualquiera,  , en la suma de un vector
, en la suma de un vector  contenido en el plano que contiene a los vectores
contenido en el plano que contiene a los vectores  y
y  más otro vector
más otro vector 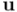 ortogonal al plano, en el lenguaje del álgebra geométrica. Eso significa extender los conceptos de proyección y exclusión, que en la entrada anterior definimos respecto a un vector, para definirlos también respecto a un bivector simple (o, aún más en general, respecto a un multivector simple).
ortogonal al plano, en el lenguaje del álgebra geométrica. Eso significa extender los conceptos de proyección y exclusión, que en la entrada anterior definimos respecto a un vector, para definirlos también respecto a un bivector simple (o, aún más en general, respecto a un multivector simple).

El vector 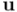 es la parte ortogonal de
es la parte ortogonal de  al bivector simple y unitario
al bivector simple y unitario  , el cual, por ser simple y unitario, lo podemos expresar como producto geométrico de dos vectores ortonormales, que llamaré
, el cual, por ser simple y unitario, lo podemos expresar como producto geométrico de dos vectores ortonormales, que llamaré  y
y  (estos vectores forman una base ortonormal del subespacio vectorial representado por el bivector simple
(estos vectores forman una base ortonormal del subespacio vectorial representado por el bivector simple  ):
):

Naturalmente podemos escribir:

para indicar que 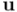 es la parte ortogonal del vector
es la parte ortogonal del vector  a la “dirección plana” dada por el bivector
a la “dirección plana” dada por el bivector  .
.
Análogamente, podemos escribir:

para indicar que  es la parte paralela de
es la parte paralela de  a la “dirección plana” dada por el bivector
a la “dirección plana” dada por el bivector  .
.
Además, como  está en el subespacio bidimensional representado por el bivector simple
está en el subespacio bidimensional representado por el bivector simple  , siempre se puede tomar uno de los dos vectores,
, siempre se puede tomar uno de los dos vectores,  o
o  , como la normalización de
, como la normalización de  . Tomemos pues:
. Tomemos pues:

Recordemos una vez más que el cuadrado del bivector  , definido más arriba, vale -1 por ser un bivector unitario. Por tanto:
, definido más arriba, vale -1 por ser un bivector unitario. Por tanto:

Concentrémonos ahora en el interior del paréntesis, que contiene el producto del vector  por el bivector
por el bivector  :
:

Desarrollemos, pues,  como suma de los vectores
como suma de los vectores 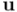 y
y  ; y
; y  como producto geométrico de los vectores unitarios
como producto geométrico de los vectores unitarios  y
y  :
:

Vemos que el producto  se puede descomponer en dos partes: una parte trivectorial, que he indicado en rojo (es el producto geométrico de tres vectores mutuamente ortogonales dos a dos, y, por tanto, también se puede reescribir como el producto exterior de los tres vectores), y una parte vectorial, que he indicado en verde (como
se puede descomponer en dos partes: una parte trivectorial, que he indicado en rojo (es el producto geométrico de tres vectores mutuamente ortogonales dos a dos, y, por tanto, también se puede reescribir como el producto exterior de los tres vectores), y una parte vectorial, que he indicado en verde (como  , el producto
, el producto  se contrae al valor
se contrae al valor  , que es lo que queda multiplicando a
, que es lo que queda multiplicando a  . Es decir, podemos escribir:
. Es decir, podemos escribir:

Donde, naturalmente,  y
y  (recordemos que la notación
(recordemos que la notación  indica la parte de grado
indica la parte de grado  del multivector
del multivector  ). Y aquí podemos hacer una comparación con la fórmula fundamental del producto geométrico de dos vectores:
). Y aquí podemos hacer una comparación con la fórmula fundamental del producto geométrico de dos vectores:

donde se presenta el producto geométrico de dos vectores como suma de una parte escalar (de grado 0), el producto interior, y de una parte bivectorial (de grado 2). En el caso del producto de un vector por un bivector, tenemos una parte de grado 1, que proviene de la parte que contiene una contracción, y una parte de grado 3, proveniente de la parte donde no hay contracciones. Por tanto, parece natural hacer una pequeña generalización de los conceptos de producto interior y de producto exterior, que hasta ahora se limitaban al producto de vectores, y extenderlo al producto de vectores por bivectores. Así, llamaremos producto interior de un vector  por un bivector
por un bivector  a la parte vectorial del producto geométrico
a la parte vectorial del producto geométrico  :
:

Y, por otra parte, llamaremos producto exterior de un vector  por un bivector
por un bivector  a la parte trivectorial del producto geométrico
a la parte trivectorial del producto geométrico  :
:

La parte trivectorial proviene de la parte de  perpendicular a la superficie orientada representada por el bivector
perpendicular a la superficie orientada representada por el bivector  ; y la parte vectorial proviene de la parte de
; y la parte vectorial proviene de la parte de  paralela a la superficie representada por
paralela a la superficie representada por  .
.
La definición general de producto interior y de producto exterior para cualquier tipo de multivectores homogéneos queda para entradas posteriores.
En resumidas cuentas, lo que tenemos es que podemos expresar la descomposición del vector  en términos del producto interior y del producto exterior del vector
en términos del producto interior y del producto exterior del vector  por el bivector
por el bivector  :
:


Del mismo modo que en la entrada anterior habíamos expresado la descomposición de un vector como suma de una parte paralela (la proyección) y una parte ortogonal (la exclusión) respecto a otro vector, aquí estamos descomponiendo un vector como suma de una parte paralela y de una parte ortogonal a una superficie orientada, dada por un bivector simple. Por tanto, podemos definir la proyección y la exclusión de un vector respecto a un bivector simple y expresarlas en el lenguaje del álgebra geométrica:
 (proyección del vector
(proyección del vector  sobre la superficie orientada representada por el bivector simple
sobre la superficie orientada representada por el bivector simple  )
)
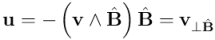 (exclusión del vector
(exclusión del vector  respecto a la superficie orientada representada por el bivector simple
respecto a la superficie orientada representada por el bivector simple  )
)
En la siguiente figura se puede visualizar el efecto de una rotación simple de “ángulo orientado”  (donde
(donde  sería el “valor escalar” del ángulo, mientras que el bivector unitario simple
sería el “valor escalar” del ángulo, mientras que el bivector unitario simple  da la orientación y sentido del ángulo de rotación) sobre un vector
da la orientación y sentido del ángulo de rotación) sobre un vector  , que es transformado en el vector rotado
, que es transformado en el vector rotado 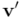 . La exclusión del vector respecto al bivector
. La exclusión del vector respecto al bivector  , o sea
, o sea  , no cambia con la rotación, de modo que la componente afectada por la rotación es la inclusión del vector respecto a
, no cambia con la rotación, de modo que la componente afectada por la rotación es la inclusión del vector respecto a  .
.

Una rotación simple en tres dimensiones. La rotación simple rota los vectores paralelos a cualquier plano que contenga el bivector unitario simple (área orientada unidad)  . Los vectores perpendiculares al área orientada
. Los vectores perpendiculares al área orientada  no quedan afectados. Como la figura representa el caso tridimensional, el subespacio de vectores que no varían bajo una rotación simple es unidimensional (se trata de los vectores perpendiculares al plano de giro), y en el caso de la figura serían los vectores paralelos al “eje de rotación” representado por la recta de puntos. Pero el concepto de “eje de rotación” sólo existe en tres dimensiones. En cuatro dimensiones, por ejemplo, podríamos encontrar un subespacio vectorial bidimensional de vectores perpendiculares al bivector simple unitario
no quedan afectados. Como la figura representa el caso tridimensional, el subespacio de vectores que no varían bajo una rotación simple es unidimensional (se trata de los vectores perpendiculares al plano de giro), y en el caso de la figura serían los vectores paralelos al “eje de rotación” representado por la recta de puntos. Pero el concepto de “eje de rotación” sólo existe en tres dimensiones. En cuatro dimensiones, por ejemplo, podríamos encontrar un subespacio vectorial bidimensional de vectores perpendiculares al bivector simple unitario  , que es el que en realidad da el plano y sentido de rotación.
, que es el que en realidad da el plano y sentido de rotación.
El concepto de “rotación en torno a un eje”, tomado de nuestra experiencia en el mundo tridimensional, es engañoso. Las rotaciones simples tienen lugar, en el caso general n-dimensional, en un plano, por así decirlo.
El teorema de Cartan-Dieudonné
Hemos visto cómo podemos obtener una rotación componiendo dos reflexiones respecto a un hiperplano, y cómo éstas rotaciones se asocian a la exponencial de un bivector simple. Una rotación que se pueda obtener de este modo diremos que es una rotación simple. Pero nada impide seguir componiendo más y más reflexiones. Como un número impar de reflexiones cambia de signo de los pseudoescalares, o volúmenes orientados, las rotaciones, que son las isometrías lineales que respetan la orientación de los pseudoescalares, se obtendrán componiendo un número par de reflexiones. Pero, ¿cuántos pares de reflexiones harán falta en general para describir cualquier rotación en un espacio lineal euclídeo de n dimesiones? Para ello necesitamos acudir al teorema de Cartan-Dieudonné, que afirma que cualquier transformación ortogonal (o isometría lineal) en un espacio bilineal simétrico[3] de n dimensiones se puede obtener componiendo como máximo n reflexiones respecto a un hiperplano (donde recordemos que como hiperplano entendemos un subespacio lineal de n – 1 dimensiones).
Como las rotaciones requieren un número par de reflexiones (de lo contrario no conservarían la orientación de los volúmenes orientados), una rotación en un espacio lineal de n dimensiones requerirá como máximo n reflexiones, si n es par, pero sólo n – 1, si n es impar. Así, por ejemplo:
En el espacio euclídeo de 2 dimensiones, cualquier rotación se puede obtener como composición de 2 reflexiones. Todas las rotaciones en 2 dimensiones son, por tanto, simples (de hecho todas tienen lugar en un mismo plano).
En el espacio euclídeo de 3 dimensiones, cualquier rotación se puede obtener también como composición de 2 reflexiones respecto a un plano (aquí, a diferencia del caso bidimensional, tenemos muchísimos planos donde elegir) o, equivalentemente, como composición de 2 simetrías respecto a dos ejes. Una tercera reflexión respecto a un plano haría que la transformación cambiara de signo la orientación de los volúmenes, y así pasaría a ser la composición de una rotación con una reflexión especular. Por tanto, en tres dimensiones, todas las rotaciones son también simples al ser todas composición de sólo un par de reflexiones: en 3 dimensiones, cualquier rotación es “en un plano”, y deja invariante cualquier vector paralelo al “eje de rotación” perpendicular a dicho plano.
En los espacios lineales de 4 dimensiones, para describir una rotación cualquiera necesitamos componer, en general, 4 reflexiones o, equivalentemente, 2 rotaciones simples, donde cada rotación actúa en un plano diferente (y además, planos no paralelos que no se corten a lo largo de una recta, cosa perfectamente posible en cuatro dimensiones).[4]
La próxima entrada tratará de las rotaciones en 3 dimensiones, que en álgebra geométrica se pueden tratar de un modo muy elegante y eficiente, en comparación con los clásicos tratamientos con matrices ortogonales que muchos posiblemente ya conozcáis.
-
En la mayoría de los textos se prefiere llamar
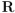 a lo que yo he denominado
a lo que yo he denominado  , y viceversa. [↩]
, y viceversa. [↩] -
Esto es consecuencia de que las rotaciones en un espacio vectorial, como las reflexiones respecto a un hiperplano o las simetrías axiales, son transformaciones lineales. En una transformación lineal siempre se cumple que la transformación de una suma de vectores es la suma de vectores transformados, y también que el producto de un escalar por un vector se transforma en el producto del escalar por el vector transformado [↩]
-
Espacio bilineal simétrico: espacio lineal en que se ha definido un producto escalar de vectores. Para nuestro caso, sirve el producto interior de vectores. Dentro de los espacios bilineales simétricos se incluyen tanto los espacios euclídeos (en que el producto interior de un vector distinto de 0 por sí mismo es siempre estrictamente positivo), como los espacios pseudoeuclídeos, como el de la Relatividad especial (en un espacio pseudoeuclídeo, una base ortogonal cualquiera del espacio lineal tiene tanto vectores de cuadrado positivo como vectores de cuadrado negativo). [↩]
-
Si los planos que se eligen para hacer las rotaciones simples se eligen de modo que se corten a lo largo de una recta, la transformación ortogonal estaría restringida a un subespacio tridimensional (no estaríamos aprovechando las cuatro dimensiones disponibles) y el resultado sería una rotación en un subespacio tridimensional, y por tanto una rotación simple. [↩]

The Explorando el álgebra geométrica 15 – La rotación simple by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.




Escribe un comentario