El Cedazo

En esta entrada se introducirán dos conceptos importantes en álgebra geométrica, el de proyección y el de exclusión de un vector respecto a otro. De hecho, no se trata más que la descomposición de un vector en una parte paralela (la proyección) y en una parte ortogonal (la exclusión) respecto a otro vector. A continuación veremos la expresión en álgebra geométrica de una simetría axial, así como también la expresión de una simetría de reflexión respecto a un hiperplano. Tanto las simetrías axiales como las reflexiones respecto a un hiperplano son ejemplos de transformaciones ortogonales. Una transformación ortogonal es aquella transformación lineal que conserva el producto interior de dos vectores, de modo que el producto interior de dos vectores es igual al de los vectores transformados. Como el producto interior define la métrica del espacio vectorial, a partir de la que se define la norma de un vector y el módulo del ángulo que forman dos vectores, las transformaciones ortogonales conservan las normas de los vectores y el módulo de los ángulos que forman cualquier par de vectores entre sí. Un tipo importante de transformaciones ortogonales son las rotaciones, pero estas quedarán ya para las próximas entradas de esta serie.

Proyección y exclusión de un vector respecto a otro

Supongamos que tenemos dos vectores, y . Vamos a suponer además que tiene norma diferente de .^[1] Por tanto, podemos normalizar el vector dividiéndolo por su norma y obtener así un vector unitario, que llamaremos :

Pues bien, como podemos escribir:

Y ahora agrupamos los dos primeros factores para hacer el producto geométrico. Recordemos la identidad fundamental, :

Así pues, hemos descompuesto el vector como suma de dos partes: la primera de ellas, , es múltiplo escalar de , y por tanto también de . Esto justifica que la etiquetemos como la parte de paralela a . En álgebra geométrica, esta parte se conoce como proyección del vector respecto al vector :

Lo habitual en los textos estándar de Matemáticas es referirse a la proyección de sobre como el escalar , pero en álgebra geométrica se prefiere reservar para este concepto la expresión proyección escalar. En álgebra geométrica la proyección (a secas) de un vector respecto a otro es también un vector.

La segunda parte de la descomposición resulta ser el vector , la parte perpendicular del vector respecto al vector . Efectivamente, el bivector se puede reescribir como el producto geométrico :

y por tanto:

Al vector , o sea, la parte perpendicular de a , se lo conoce en álgebra geométrica como la exclusión del vector respecto al vector .^[2]

La simetría axial

Consideremos ahora este producto, parecido a la expresión de la que partíamos antes:

Sabemos que este producto tiene que dar como resultado un vector, por lo visto hacia el final de la entrada 11. Intentemos expresarlo en términos de la proyección y la exclusión de respecto a .

Por un lado, es un escalar, y por tanto conmuta con . Por otro, como ya hemos visto, el producto exterior es igual al producto geométrico , producto geométrico que anticonmuta, por tratarse de un producto de vectores ortogonales, circunstancia que nos pone en bandeja la aplicación de la propiedad asociativa del producto geométrico en el segundo término y dejarlo con un aspecto muy simple:

El producto resulta ser el vector simétrico al vector respecto al eje dado por el vector . Al hacer la simetría axial, la proyección del vector respecto al eje se conserva, mientras que la exclusión del vector respecto al eje cambia de signo.

La simetría axial es una transformación ortogonal o isometría vectorial. Con esta palabra los matemáticos quieren decir que es una transformación que conserva las longitudes de cualquier vector del espacio. Las transformaciones ortogonales también conservan el módulo de los ángulos que forman entre sí los vectores cuando estos son transformados. La expresión isometría vectorial viene de la comparación con el concepto de isometría en el espacio afín (que es el espacio formado por puntos, a diferencia del concepto de espacio vectorial, que es aquel cuyos elementos son vectores libres). En un espacio afín, una isometría es una transformación que también conserva longitudes y módulos de ángulos, y sería cualquier combinación de traslaciones, simetrías, reflexiones y rotaciones. Por tanto, es un movimiento rígido en el espacio, movimiento que puede ser directo, como traslaciones y rotaciones, o inverso, que sería el caso de una reflexión respecto a un hiperplano, que cambian de signo la orientación de los pseudoescalares. En el espacio vectorial no se consideran las traslaciones, porque un vector libre se considera siempre el mismo sea cual sea su punto de aplicación: por tanto las transformaciones ortogonales son, como veremos, combinaciones de reflexiones y rotaciones.

La fórmula obtenida para la simetría axial corresponde, en efecto, a una isometría vectorial: la distancia entre dos puntos está expresada por la norma del vector que los separa, que vale . La norma del vector resultante de la reflexión, será:

Que efectivamente, coincide con la norma del vector de partida. Como podéis ver, la fórmula de la simetría es un producto de vectores no nulos, o sea un versor, como sabemos desde la entrada 11, y el cálculo acaba reduciéndose a hacer un producto de versores con contracciones en cascada.

Una isometría también conserva el módulo del ángulo que forman dos vectores: en el caso de la simetría axial, podemos considerar que si tenemos dos vectores y que forman entre sí un cierto ángulo de módulo , los respectivos vectores transformados y forman también un ángulo con el mismo módulo .

Recordemos la fórmula:

Análogamente, para el par de respectivos vectores transformados, tendremos:

Como ya hemos visto, y . Para ver que basta comprobar que el producto interior se conserva bajo una simetría axial:

Y, por tanto, el módulo del ángulo que forman entre sí los vectores transformados es igual al que forman los respectivos vectores originales.

La simetría respecto a un hiperplano (o reflexión)

Consideremos esta expresión:

Que no es más que la expresión de la simetría axial cambiada de signo. Por tanto, valdrá:

Lo que tenemos en este caso es que la exclusión respecto al vector sigue igual después de la transformación, pero la proyección respecto a cambia de signo. Suponiendo que estamos en un espacio vectorial de n dimensiones, todos los vectores perpendiculares a , que forman un subespacio de n-1 dimensiones, no quedarán modificados por la transformación, y los vectores con el mismo sentido que (que forman un subespacio unidimensional) cambiarán de signo. Por tanto, lo que describe la transformación es una reflexión del vector respecto al hiperplano ortogonal al vector .

En un espacio de n dimensiones, un hiperplano es un subespacio de n-1 dimensiones perpendicular a un vector. En dos dimensiones, un hiperplano seria un espacio de dimensión 2-1 = 1, o sea, una línea recta perpendicular a un vector normal. En el espacio de 3 dimensiones, un hiperplano es un plano bidimensional normal y corriente, cuya dirección puede definirse por su perpendicularidad a un cierto vector (denominado vector normal al plano). En un espacio de 4 dimensiones, un hiperplano es un subespacio de 3 dimensiones ortogonal a cierto vector (el vector normal al hiperplano en cuestión), y así sucesivamente.

Una reflexión respecto a un hiperplano cambia el signo de los pseudoescalares

Consideremos el pseudoescalar canónico de que nos da la unidad de “hipervolumen orientado” en :

Y veamos cómo le afecta la reflexion respecto a un hiperplano ortogonal a un cierto vector .

Como no es obligatorio expresar el pseudoescalar canónico en términos de la base canónica original , , … , podemos introducir una nueva base ortonormal con la misma orientación , … , de modo que el primer vector de la nueva base coincida con la normalización del vector .

El pseudoescalar canónico se expresaría análogamente:

En esta base es muy fácil ver que el efecto de la reflexión sobre el pseudoescalar es cambiarlo de signo. Llamemos al pseudoesalar resultado de la reflexión:

Como , para tendremos (el vector normal al hiperplano cambia de sentido en la reflexión) y para tendremos 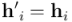(los vectores dentro del hiperplano no cambian). De ahí que el pseudoescalar unitario canónico cambie de signo bajo una reflexión respecto a un hiperplano.

En la figura de abajo podemos ver un ejemplo en tres dimensiones. En tres dimensiones los hiperplanos son los planos bidimensionales ordinarios. La mano izquierda y la mano derecha son simétricas respecto a un (hiper)plano de simetría (no representado en la figura): una es la reflexión de la otra respecto al plano de simetría. A cada mano se asocia una base ortonormal de vectores, cada una simétrica de la otra respecto al plano de simetría. El hecho de que un pseudoescalar cambie de signo bajo una reflexión respecto a un hiperplano se manifiesta en que no es posible convertir una mano (o su base ortonormal asociada) en la otra utilizando exclusivamente traslaciones y rotaciones, ya que ni traslaciones ni rotaciones pueden cambiar de signo un pseudoescalar: por mucho que intentemos mover y rotar una mano izquierda en el espacio, no la podemos convertir en una mano derecha, y viceversa. Una isometría que no cambie el signo de los pseudoescalares se podrá imaginar siempre como una combinación de traslaciones y rotaciones. Una isometría que, en cambio, produzca un cambio de signo de los pseudoescalares se podrá imaginar siempre como una combinación de traslaciones, rotaciones más una reflexión respecto a un hiperplano.

El comportamiento del signo de los pseudoescalares respecto a las simetrías axiales es un poco más complicado, porque depende de si la dimensión n del espacio vectorial es par o impar.

Cuando n es par, una simetría axial cambia el signo de los pseudoescalares, porque los vectores en el subespacio (n-1)-dimensional cambian de signo, mientras los vectores paralelos al eje de simetría (que forman un espacio unidimensional) no lo hacen. De ahí resulta un número impar de cambios de signo en los pseudoescalares. Por ejemplo, si n vale 2, una simetría axial equivale siempre a una reflexión respecto al hiperplano (unidimensional) que resulta ser el propio eje de simetría axial. En dos dimensiones, tras una simetría axial, el retrato de una cara de perfil que mira a la izquierda (o, respectivamente, a la derecha) se transforma en un retrato de una cara que mira a la derecha (o, respectivamente, a la izquierda), y no es posible superponer una imagen sobre su simétrica haciendo traslaciones y rotaciones en el plano.

Cuando n es impar, una simetría axial no cambia el signo de los pseudoescalares, ya que hay en total un número par (n-1) de cambios de signo en los vectores de una base del subespacio ortogonal al eje de simetría. Por ejemplo, si n vale 3, una simetría axial es exactamente lo mismo que una rotación de 180º en torno al eje de simetría, que es un movimiento directo y no lleva asociado cambio de signo de los pseudoescalares: una mano izquierda (o, respectivamente, derecha) sigue siendo una mano izquierda (o, respectivamente, derecha) tras una simetria axial en tres dimensiones, porque simplemente ha sufrido una rotación de 180º respecto al eje de simetría.

Ejemplo 1: simetría axial en dos dimensiones

Tenemos el vector . Calculemos la simetría axial respecto a un eje que siga la dirección del vector . Normalicemos :

Y ya podemos calcular la correspondiente simetría axial:

Ejemplo 2: simetrías y reflexiones en tres dimensiones

Calculemos la simetría axial de los vectores:

y

respecto al eje dado por el vector:

cuya normalización vale:

Comencemos por el simétrico del vector :

No es difícil ver que las partes trivectoriales, que he marcado en gris, se anulan todas entre sí, como tiene que ser, y como sabíamos desde el principio que tenía que pasar. En álgebra geométrica es frecuente encontrarse con situaciones en que sabemos de antemano que el resultado de una operación con multivectores tiene que dar solamente términos de un grado determinado, cosa que se puede aprovechar para ignorar directamente aquellos términos que sabemos que no van a contribuir al resultado final, y que resulta muy útil cuando hay muchos de estos términos (eso sí, hay que tener la seguridad de no haber cometido errores de cálculo). Por tanto, tenemos finalmente:

Observemos de pasada que no tiene componente paralela a (que en la figura de más abajo, da el sentido positivo del eje Z), y, por tanto, se encuentra en el plano de los vectores y , que, respectivamente, dan los sentidos positivos de los ejes X e Y, como podréis ver en la figura.

Pasemos a hacer la simetría axial del vector respecto al vector :

¿Qué sucederá cuando hagamos la combinación de dos reflexiones? Si las hacemos respecto al mismo plano obtendremos la transformación identidad, es decir, la transformación deja todo como estaba inicialmente. Pero si reflejamos respecto a hiperplanos que forman un ángulo entre sí, obtenemos una nueva transformación. Como cada reflexión cambia una vez el signo de los pseudoescalares, el resultado de dos reflexiones no cambiará el signo de los pseudoescalares y, por tanto, no puede ser una reflexión. ¿Qué tipo de transformaciones lineales dejan invariantes a los pseudoescalares? Las rotaciones: de las rotaciones como composición de reflexiones (o simetrías axiales) tratará la próxima entrada.

1. En espacios de métrica euclídea, eso equivale a decir que es diferente de , pero en espacios de métrica pseudoeuclídea, como el que se utiliza en la relatividad especial, sí pueden existir vectores diferentes de con norma igual a . [↩]

2. En los textos en inglés, el término utilizado habitualmente es rejection, que alguna que otra vez he visto traducir como “rechazo” o incluso como “reyección”. Como ninguna de esas traducciones me acaba de satisfacer, me he quedado finalmente con exclusión. [↩]