En esta nueva entrada de la serie dedicada al álgebra geométrica se presentarán las involuciones más importantes: la involución de paridad (o involución de grado) y la reversión. Las involuciones tienen a menudo, sobre todo la reversión, un papel parecido a la conjugación en el caso de los números complejos o los cuaterniones. También conviene saber cómo se comportan los multivectores homogéneos de un determinado grado: a menudo eso permite afirmar cosas sobre el resultado de un cierto producto de multivectores. Introduciré también el concepto de versor, un tipo de objeto muy habitual e importantísimo en álgebra geométrica: veremos en entradas posteriores que los operadores de reflexión y de rotación son versores.
En los números complejos y en los cuaterniones teníamos la conjugación, mediante la cual pasábamos de un número complejo o cuaternión a su versión conjugada, en que, respectivamente, la parte imaginaria del complejo o la parte vectorial del cuaternión cambiaban de signo. La conjugación es una forma de involución, aquel tipo de función que se caracteriza por que aplicada dos veces seguidas devuelve el valor original: tenemos así que el conjugado del conjugado de un complejo o de un cuaternión es el complejo o cuaternión de partida.
En las álgebras geométricas disponemos de más de una forma de involución. La primera que veremos es la involución de grado, o involución de paridad, que consiste en el cambio de signo de todos los vectores. El efecto de una involución de grado sobre un escalar es no modificarlo (siempre podemos imaginar a los escalares como el producto geométrico de dos vectores paralelos: al cambiar de signo los vectores, el signo del escalar no cambia, al ser el producto de dos de ellos). Los vectores (multivectores de grado 1) ya sabemos que cambian de signo. A los bivectores les pasa como a los escalares: como se pueden pensar como productos geométricos de dos vectores ortogonales o sumas de productos geométricos de pares de vectores ortogonales, tampoco cambian de signo. Los trivectores, al ser sumas de productos geométricos de tripletas de vectores mutuamente ortogonales entre sí, volverán a cambiar de signo bajo involución de grado. En general, las partes de grado par de un multivector  no cambian de signo bajo una involución de grado, mientras que las partes de grado impar sí lo hacen. Indicaré con una barra por encima la involución de grado:[1]
no cambian de signo bajo una involución de grado, mientras que las partes de grado impar sí lo hacen. Indicaré con una barra por encima la involución de grado:[1]

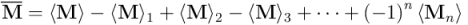
La parte de grado j de la involución de paridad es por tanto  y cambia de signo o no según sea j par o impar: para j par no cambiará de signo, pero si j es impar sí lo hará.
y cambia de signo o no según sea j par o impar: para j par no cambiará de signo, pero si j es impar sí lo hará.
La reversión
La reversión es, sin duda, la involución más importante que veremos. Consiste en la inversión del orden de todos los productos geométricos de vectores. Veamos su efecto en cada tipo de multivector homogéneo (multivector homogéneo es aquel cuyos términos son todos del mismo grado):
1) Los escalares no cambian de signo bajo una reversión.
2) Los vectores tampoco cambian de signo bajo una reversión, como los escalares.
3) Los bivectores sí cambian de signo bajo una reversión. Como los podemos expresar como combinaciones lineales de productos geométricos de parejas de vectores diferentes de la base ortonormal, y los productos geométricos de vectores ortogonales entre ellos son a la vez productos exteriores y, por tanto, anticonmutan, la reversión produce el cambio de signo de los bivectores. Veamos un ejemplo concreto y hagamos la reversión de este bivector de  , que expresamos en términos de una base de productos de vectores ortonormales:
, que expresamos en términos de una base de productos de vectores ortonormales:

La reversión de un multivector se indica con una tilde por encima, o también con una daga en posición de superíndice:

En vez de  , podríamos haber escrito
, podríamos haber escrito  , utilizando la notación con daga.[2]
, utilizando la notación con daga.[2]
Y ahora reexpresamos el resultado en términos de la base de bivectores de que partíamos, con el orden original:

Efectivamente, vemos que los bivectores cambian de signo bajo una reversión.
3) Los trivectores también cambian de signo bajo una reversión, como los bivectores. Veamos como ejemplo este trivector de  :
:
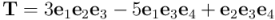
La reversión será la suma las reversiones de cada término. Como antes, en el caso de los bivectores, para comparar con el trivector de partida debemos reexpresarla en la base de trivectores de partida. Para ello, bastará intercambiar en cada término el primer vector del producto geométrico con el último (para resaltarlos he puesto con el mismo color los vectores a intercambiar) … y ese intercambio de vectores producirá un cambio de signo respecto al trivector  :
:

Al volver a ponerlos en el orden original vemos que los trivectores, al igual que los bivectores, cambian de signo bajo una reversión. Tanto en un caso como en otro hay que transponer un solo par (= un solo cambio de signo) de vectores en cada término, cuando los expresamos en una base canónica.
Un momento… no tan rápido. En principio tenemos cambio de signo cuando se cambia el orden del producto exterior de dos vectores consecutivos. En el caso de los bivectores intercambiamos directamente vectores consecutivos en el producto, porque sabemos que 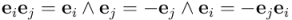 , cuando
, cuando  . Pero en el caso de los trivectores, ¿tenemos derecho a trasponer pares de vectores no contiguos y decir que estos intercambios producen un cambio de signo? Pues sí. De hecho, no importa cuántos vectores haya entre los dos vectores que se intercambian en un producto exterior: el intercambio de un par de vectores cualesquiera en un producto exterior produce un cambio de signo. La explicación se detalla en la figura que sigue, donde intercambiamos paso a paso la posición de los vectores
. Pero en el caso de los trivectores, ¿tenemos derecho a trasponer pares de vectores no contiguos y decir que estos intercambios producen un cambio de signo? Pues sí. De hecho, no importa cuántos vectores haya entre los dos vectores que se intercambian en un producto exterior: el intercambio de un par de vectores cualesquiera en un producto exterior produce un cambio de signo. La explicación se detalla en la figura que sigue, donde intercambiamos paso a paso la posición de los vectores  y
y  , que están separados por m vectores en un producto exterior.
, que están separados por m vectores en un producto exterior.

El intercambio de dos factores en un producto exterior de vectores produce un cambio de signo, aunque los vectores intercambiados no sean consecutivos. La explicación es que el intercambio de dos vectores en el producto exterior equivale siempre a un número impar (2m + 1, en el caso ilustrado) de intercambios de parejas de vectores consecutivos. Debajo de la llave horizontal se indica el número de vectores que abarca.
4) Los cuadrivectores no cambian de signo bajo una reversión. Pensemos en un cuadrivector expresado en una base canónica de productos de vectores ortonormales, por ejemplo este:
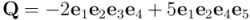
Podemos hacer la reversión de 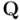 haciendo dos transposiciones de vectores en cada término. La primera transposición sería entre el primer y el último de los vectores de cada producto, que he marcado en azul, y la segunda transposición sería entre el segundo vector por la izquierda y el segundo vector por la derecha de cada producto, que he marcado en verde. Como en cada término se hacen dos transposiciones, no hay cambio de signo respecto al cuadrivector no revertido:
haciendo dos transposiciones de vectores en cada término. La primera transposición sería entre el primer y el último de los vectores de cada producto, que he marcado en azul, y la segunda transposición sería entre el segundo vector por la izquierda y el segundo vector por la derecha de cada producto, que he marcado en verde. Como en cada término se hacen dos transposiciones, no hay cambio de signo respecto al cuadrivector no revertido:

5) Los 5-vectores tampoco cambian de signo bajo una reversión, al igual que los cuadrivectores. Podemos ver que para revertir un 5-vector, que podemos suponer expresado como combinación lineal de una base canónica de 5-vectores, bastan, como en el caso de los cuadrivectores, dos transposiciones en cada término: en la primera transponemos el primer vector y el último, y en la segunda, el segundo vector por la izquierda con el segundo vector por la derecha. El vector que está en el centro queda desaparejado y no se mueve. Ejemplo:


A partir de aquí es fácil ver que tanto los 6-vectores como los 7-vectores cambian de signo: tanto en un caso como en otro hay que trasponer tres pares de vectores por cada término (el primero con el último, el segundo por la izquierda con el segundo por la derecha y el tercero por la izquierda con el tercero por la derecha), con el consiguiente cambio de signo, por ser 3 un número impar. Los 8-vectores y 9-vectores no cambian de signo, porque requieren un número par de transposiciones (cuatro), y así sucesivamente. Por tanto, dado un multivector genérico  de una álgebra geométrica
de una álgebra geométrica  :
:

Su reversión,  , será:
, será:

El signo de los términos va oscilando según la regla: más, más, menos, menos, más, más, menos, menos, etc. Se puede ver que, en general la parte de grado j de  será:
será:

El factor 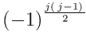 proporciona exactamente el signo de la reversión de la parte de grado j, como es fácil comprobar.
proporciona exactamente el signo de la reversión de la parte de grado j, como es fácil comprobar.
Una forma de obtener esta expresión para el signo de la reversión de un multivector homogéneo de grado j es hacer la reversión con este otro método: en cada término de grado j de la expresión del multivector como combinación lineal de elementos de la base canónica se hace saltar el vector situado más a la izquierda j – 1 posiciones más hacia la derecha, tras lo cual haremos saltar el vector que haya quedado más a la izquierda j – 2 posiciones hacia la derecha, tras lo cual haremos saltar el vector que haya quedado más a la izquierda j - 3 posiciones hacia la derecha… para acabar haciendo saltar el vector que queda más a la izquierda (y que al principio de todo era el segundo por la derecha) una posición hacia la derecha, por encima del vector que al principio estaba a la derecha del todo. En total se habrán hecho:

transposiciones. La suma se obtiene de la correspondiente fórmula para sumar los términos una progresión aritmética. Naturalmente, como la reversión es un concepto bien definido, el número de transposiciones necesarias para realizarla no puede cambiar de par a impar, o viceversa, si cambiamos el método utilizado para obtenerla.
La reversión es una antiinvolución
La reversión de un producto geométrico de multivectores es igual al producto geométrico de las reversiones de los factores, pero tomándolos en orden inverso:
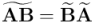
O, si utilizamos la notación con dagas:

No es difícil de entender. Consideremos un ejemplo muy sencillo:



Por otro lado:

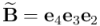
Y finalmente:

Por ello, se dice que la reversión es una antiinvolución. La involución de grado, en cambio, no es una antiinvolución, porque cumple:

Es decir, la involución de grado de un producto geométrico es directamente el producto geométrico de involuciones de grado, sin cambiar el orden.
Versores
Una clase de multivectores muy importante en álgebra geométrica son los versores.[3] Versores son aquellos multivectores que resultan de multiplicar un cierto número m de vectores invertibles. Un versor  será entonces:[4]
será entonces:[4]

Donde los vectores  pueden ser cualquier vector invertible.
pueden ser cualquier vector invertible.
Podemos ver inmediatamente que el producto de  por su reversión (no importa por qué lado, porque conmutan, como es fácil verificar) da un número real y estrictamente positivo:
por su reversión (no importa por qué lado, porque conmutan, como es fácil verificar) da un número real y estrictamente positivo:


He marcado en color verde los dos vectores que se multiplican contiguamente en posición central. Como son el mismo vector, su producto sigue la ley de contracción y da el cuadrado de la norma del vector, que es un número real y podemos pasarlo a multiplicar por delante. Tras ello podemos seguir haciendo contracciones en cascada:




El resultado es el producto de m números reales diferentes de 0 y positivos y, por tanto, también será un valor estrictamente positivo.
También vemos que podemos calcular el inverso de un versor: es simplemente la reversión del versor dividida por el producto  que acabamos de calcular:
que acabamos de calcular:
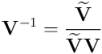
Y, efectivamente, se cumple:

Algunos ejemplos de aplicación de las propiedades de las involuciones
Muchas veces el comportamiento de un producto de multivectores bajo un tipo de involución permite hacer afirmaciones sobre el resultado de la operación, en concreto, sobre la presencia o no de partes de cierto grado. Comencemos con un resultado muy útil:
Un versor que resulte de multiplicar m vectores será un multivector con partes de sólo grado impar o sólo grado par, según sea m, respectivamente, un número impar o un número par. Además, no es posible tener en el resultado partes de grado superior a m, así como tampoco puede haber partes de grado superior a n, la dimensión del espacio vectorial en que nos encontremos.
Efectivamente, consideremos el versor  . Veamos cómo se comporta bajo una involución de grado que, como sabemos, es el cambio de signo de todos los vectores:
. Veamos cómo se comporta bajo una involución de grado que, como sabemos, es el cambio de signo de todos los vectores:

Y queda inmediatamente claro que que el versor  cambiará de signo al sufrir una involución de grado si m es impar, o bien no cambiará de signo si m es par. Si pasa lo primero,
cambiará de signo al sufrir una involución de grado si m es impar, o bien no cambiará de signo si m es par. Si pasa lo primero, sólo puede contener términos de grado impar, porque sólo los términos de grado impar cambian de signo bajo paridad. Si pasa lo segundo,
sólo puede contener términos de grado impar, porque sólo los términos de grado impar cambian de signo bajo paridad. Si pasa lo segundo, sólo puede contener términos de grado par, porque sólo los términos de grado impar no cambian de signo bajo paridad.
sólo puede contener términos de grado par, porque sólo los términos de grado impar no cambian de signo bajo paridad.
En cuanto a que no es posible que el resultado contenga términos de grado superior a m, es lógico. Con los m vectores que estamos multiplicando es imposible generar por combinación lineal un espacio lineal de más de m dimensiones, y al multiplicarlos entre sí forzosamente tendremos que generar multivectores dentro de la subálgebra geométrica  , donde el grado máximo es precisamente m. O dicho más simplemente, multiplicando m objetos de grado 1, como máximo sólo podremos llegar a producir objetos de grado m.
, donde el grado máximo es precisamente m. O dicho más simplemente, multiplicando m objetos de grado 1, como máximo sólo podremos llegar a producir objetos de grado m.
Y, por supuesto, tampoco se puede superar el grado n, correspondiente a la dimensionalidad del espacio de partida: no esperéis encontrar cuadrivectores en un producto geométrico de cuatro vectores que “habitan” en un mismo (sub)espacio bidimensional, por ejemplo: el resultado en un caso como este sólo puede contener términos escalares y bivectoriales.
Así, por ejemplo:
En el caso en que m vale 2:
Un producto geométrico de dos vectores,  , tiene que dar como resultado la suma de un escalar y de un bivector. Bueno… este resultado hace unas cuantas entradas que ya lo conocíamos, ¿verdad?
, tiene que dar como resultado la suma de un escalar y de un bivector. Bueno… este resultado hace unas cuantas entradas que ya lo conocíamos, ¿verdad?

Donde naturalmente,  y
y 
Y para m = 3:
El producto geométrico de tres vectores cualesquiera,  tiene que dar como resultado una suma de multivectores homogéneos de grado impar, como mucho la suma de un vector y de un trivector, quedando excluidos otros grados:
tiene que dar como resultado una suma de multivectores homogéneos de grado impar, como mucho la suma de un vector y de un trivector, quedando excluidos otros grados:

De este resultado podemos obtener otros:
1) Propiedad permutativa del producto de tres vectores linealmente dependientes.Un interesante caso particular del producto geométrico de tres vectores es cuando los tres vectores no son linealmente independientes. Sería el caso, por ejemplo, en que los tres vectores estén en un mismo plano. Como tres vectores linealmente dependientes no pueden generar un espacio lineal tridimensional, el álgebra geométrica asociada no puede contener trivectores. Tendremos, por tanto, que  es un vector, y como todo vector es igual a su reversión, tendremos este resultado:
es un vector, y como todo vector es igual a su reversión, tendremos este resultado:
Los vectores  ,
,  y
y  son linealmente dependientes
son linealmente dependientes 
Como se indica, la implicación también funciona de derecha a izquierda, ya que la parte trivectorial de un triple producto geométrico de vectores es precisamente el producto exterior de los tres vectores, que se anula cuando los tres vectores son linealmente dependientes, y por tanto si el producto de tres vectores da lo mismo que su reverso, los tres vectores son linealmente dependientes. Esto se conoce como propiedad permutativa del producto de tres vectores linealmente dependientes, y se utiliza a menudo en problemas de geometría plana.
2) Un producto de vectores de la forma  da siempre como resultado un vector.
Antes ya hemos visto que el producto de tres vectores es la suma un vector y de un trivector (como mucho). En este caso, tenemos el producto de tres vectores, pero ahora el primero y el último vector es el mismo. El comportamiento de este producto bajo la reversión permite excluir que tenga componente trivectorial. Efectivamente, este producto es igual a su reversión:
da siempre como resultado un vector.
Antes ya hemos visto que el producto de tres vectores es la suma un vector y de un trivector (como mucho). En este caso, tenemos el producto de tres vectores, pero ahora el primero y el último vector es el mismo. El comportamiento de este producto bajo la reversión permite excluir que tenga componente trivectorial. Efectivamente, este producto es igual a su reversión:

Pero la reversión cambia de signo la parte trivectorial (y no la parte vectorial). La conclusión es inmediata:  no puede tener parte trivectorial, y por lo tanto tiene que ser un vector.
no puede tener parte trivectorial, y por lo tanto tiene que ser un vector.
Esta conclusión también podríamos haberla deducido siguiendo la línea de razonamiento hecha en el apartado 1), ya que de los “tres” vectores que forman el producto, uno está repetido, y por tanto, no tenemos una tripleta de vectores linealmente independientes.
De este resultado que acabamos de obtener se deduce de forma inmediata otro más todavía…
3) Un producto de la forma  , donde
, donde  es un vector y
es un vector y  es un versor da siempre como resultado un vector.
es un versor da siempre como resultado un vector.
Al expresar  como producto de vectores tendremos que el producto que buscamos tendrá esta forma:
como producto de vectores tendremos que el producto que buscamos tendrá esta forma:


Y queda meridianamente claro que el paréntesis más interno es un vector, por tratarse del caso 2) analizado antes. Pero, por la misma razón, el paréntesis que lo envuelve también tiene que dar como resultado un vector, y así sucesivamente. En álgebra geométrica encontraremos muy a menudo expresiones de este tipo.
-
He decidido indicar la involución de grado con una barra por encima. Las convenciones de notación no están muy asentadas en álgebra geométrica, y es muy posible que en otros textos veáis otros símbolos para indicar la involución de grado. De hecho, el que se ve más habitualmente en los textos es posiblemente el símbolo de circunflejo (^), pero como yo ya lo utilizo para indicar la normalización de un (multi)vector (como es habitual entre los físicos), he preferido usar otra opción. [↩]
-
Mientras trabajamos en una sola álgebra geométrica, no tiene sentido usar dos notaciones diferentes para la reversión. Pero hay casos en que hace falta usar dos símbolos diferentes para la reversión: eso ocurre en relatividad especial, ya que entonces conviene distinguir la reversión propia del álgebra
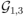 y la reversión relativa al espacio tridimensional ortogonal a un cierto vector de tipo temporal, asociado a su vez a un observador en un sistema de referencia inercial. En estos casos, el primer tipo de reversión se indica con la tilde, y el segundo con la daga. La daga se usa exclusivamente cuando tenemos métrica euclídea. Quienes hayan estudiado Mecánica Cuántica sabrán que la daga se utiliza para indicar el conjugado hermítico de un operador matricial. Eso no es casualidad: toda álgebra asociativa (y las álgebras geométricas lo son) se puede representar por un álgebra de matrices cuadradas, y resulta que la reversión de un bivector en una álgebra geométrica asociada a un espacio de métrica euclídea se corresponde con el conjugado hermítico de la matriz que lo representa. [↩]
y la reversión relativa al espacio tridimensional ortogonal a un cierto vector de tipo temporal, asociado a su vez a un observador en un sistema de referencia inercial. En estos casos, el primer tipo de reversión se indica con la tilde, y el segundo con la daga. La daga se usa exclusivamente cuando tenemos métrica euclídea. Quienes hayan estudiado Mecánica Cuántica sabrán que la daga se utiliza para indicar el conjugado hermítico de un operador matricial. Eso no es casualidad: toda álgebra asociativa (y las álgebras geométricas lo son) se puede representar por un álgebra de matrices cuadradas, y resulta que la reversión de un bivector en una álgebra geométrica asociada a un espacio de métrica euclídea se corresponde con el conjugado hermítico de la matriz que lo representa. [↩] -
Ojo, otros autores, siguiendo a Hamilton, llaman versores a lo que en esta serie llamo vector unitario, que es un concepto completamente diferente. [↩]
-
En espacios de métrica euclídea, cualquier vector diferente de 0 es invertible, siendo el inverso del vector
 , como ya sabemos,
, como ya sabemos, 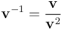 . En espacios de métrica pseudoeuclídea, como el de la relatividad especial, es inevitable la existencia de vectores diferentes de 0 pero con cuadrado nulo, los llamados vectores de tipo luz o simplemente vectores nulos, que no tienen inverso. De momento, como tratamos con espacios de métrica euclídea, no nos preocuparemos de ellos y podemos pensar que un versor es un producto de vectores diferentes de 0. [↩]
. En espacios de métrica pseudoeuclídea, como el de la relatividad especial, es inevitable la existencia de vectores diferentes de 0 pero con cuadrado nulo, los llamados vectores de tipo luz o simplemente vectores nulos, que no tienen inverso. De momento, como tratamos con espacios de métrica euclídea, no nos preocuparemos de ellos y podemos pensar que un versor es un producto de vectores diferentes de 0. [↩]

The Explorando el álgebra geométrica 11 – Involuciones: involución de grado y reversión. Versores by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.




Escribe un comentario