En las dos entradas anteriores de esta serie sobre álgebra geométrica, esta y esta otra, se ha hablado del conjunto  de los números complejos, cuyo origen está en la necesidad dar sentido a la extracción de raíces cuadradas de números negativos. En los complejos no sólo es posible sacar raíces cuadradas (o de cualquier otro orden) de cualquier número, sino incluso logaritmos. Por lo que respecta a eso, ya no hacía falta crear ningún nuevo conjunto numérico…
de los números complejos, cuyo origen está en la necesidad dar sentido a la extracción de raíces cuadradas de números negativos. En los complejos no sólo es posible sacar raíces cuadradas (o de cualquier otro orden) de cualquier número, sino incluso logaritmos. Por lo que respecta a eso, ya no hacía falta crear ningún nuevo conjunto numérico…
Sin embargo, tanto la representación en el plano de los números complejos como el modo en que el producto de complejos unitarios representaba el grupo de rotaciones en el plano hizo inevitable que los matemáticos se preguntaran si sería posible generalizar aún más los números complejos, de forma que se obtuviera un sistema de números hipercomplejos que pudiera tener una representación en el espacio tridimensional y donde se pudiera encontrar algún tipo de números que representaran las rotaciones en el espacio tridimensional. De hecho, Caspar Wessel, como ya os mencioné en la segunda entrada dedicada a los complejos, el primer matemático que encontró la interpretación gráfica de dichos números complejos, hizo un primer intento fracasado en su publicación sobre los números complejos de 1799. Pero quien conseguiría encontrarlo fue Sir William Rowan Hamilton (1806-1865), protagonista de la entrada de hoy.
Hamilton había sido niño prodigio[1] y había hecho importantes contribuciones a los campos de la física y la astronomía. En 1843, Hamilton llevaba un buen tiempo[2] intentando generalizar los números complejos a tres dimensiones.

William Rowan Hamilton, como presidente de la Real Academia de Irlanda (Wikimedia)
La idea con la que trabajaba Hamilton fue introducir una segunda unidad imaginaria,  , a los números complejos, de forma que tanto
, a los números complejos, de forma que tanto
 como
como 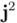 fueran iguales a
fueran iguales a  .[3] De este modo, estos hipercomplejos tendrían tres componentes, una real y dos imaginarias. La suma y resta de estas tripletas no ofrecía ningún problema, ya que se reducía a una suma formal, componente a componente, como en el caso de los complejos. Lo problemático era multiplicarlos, y en concreto asignar un valor consistente al producto
.[3] De este modo, estos hipercomplejos tendrían tres componentes, una real y dos imaginarias. La suma y resta de estas tripletas no ofrecía ningún problema, ya que se reducía a una suma formal, componente a componente, como en el caso de los complejos. Lo problemático era multiplicarlos, y en concreto asignar un valor consistente al producto  . Si se suponía que daba un número real, por ejemplo
. Si se suponía que daba un número real, por ejemplo  , había que llegar a la conclusión, de que
, había que llegar a la conclusión, de que era múltiplo real de
era múltiplo real de  , en nuestro ejemplo
, en nuestro ejemplo 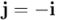 , y por tanto no es una unidad independiente de
, y por tanto no es una unidad independiente de  . Y si se suponía que el producto
. Y si se suponía que el producto  daba un resultado imaginario, la conclusión es que
daba un resultado imaginario, la conclusión es que  era real, y por tanto, tampoco era una unidad nueva. De hecho, Hamilton estaba en la misma situación en que se vio Wessel a finales del siglo XVIII. Así que cuando el hijo de Hamilton le preguntaba a su padre si sabía multiplicar tripletas, él le tenía que responder: “No, hijo mío. De momento, sólo sé sumarlas y restarlas“. Pero eso cambió el 16 de octubre de 1843.
era real, y por tanto, tampoco era una unidad nueva. De hecho, Hamilton estaba en la misma situación en que se vio Wessel a finales del siglo XVIII. Así que cuando el hijo de Hamilton le preguntaba a su padre si sabía multiplicar tripletas, él le tenía que responder: “No, hijo mío. De momento, sólo sé sumarlas y restarlas“. Pero eso cambió el 16 de octubre de 1843.
Ese día, como cuenta el propio protagonista, se encontraba Hamilton paseando con su mujer por el puente de Brougham, también conocido como puente de Broom (Broom Bridge), y súbitamente se le ocurrió la idea: introducir una nueva unidad imaginaria  , además de
, además de  y
y  , de forma que
, de forma que  , y renunciar a la conmutatividad del producto, que hasta ahora era una propiedad fundamental tanto de los números reales como de los complejos. En resumen, las tres unidades imaginarias tenían que cumplir esta regla:
, y renunciar a la conmutatividad del producto, que hasta ahora era una propiedad fundamental tanto de los números reales como de los complejos. En resumen, las tres unidades imaginarias tenían que cumplir esta regla:

De la regla anterior se puede deducir la no conmutatividad. Partamos de :

Multipliquemos ambos miembros de la igualdad por  , por la derecha:
, por la derecha:

Como  , tenemos:
, tenemos:

Como sí asumimos que la multiplicación por un número real conmuta con cualquier unidad imaginaria, tendremos:

Tras multiplicar por  ambos lados queda simplemente:
ambos lados queda simplemente:

Pero, ¿qué pasa si en vez de multiplicar la igualdad de partida por  por la derecha, se multiplica por
por la derecha, se multiplica por  por la izquierda?:
por la izquierda?:

Aplicando la propiedad asociativa, a la que no renunciamos, la igualdad anterior se transforma en:

Y a continuación, sucesivamente:

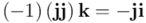
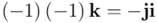

Y finalmente, por tanto:

Es decir, por un lado  , pero por otro
, pero por otro  : el producto
: el producto  anticonmuta, cambia de signo al cambiar el orden de los factores. Del mismo modo, se pueden demostrar estas igualdades:
anticonmuta, cambia de signo al cambiar el orden de los factores. Del mismo modo, se pueden demostrar estas igualdades:


Y asimismo tendremos:


Hamilton acababa de descubrir el primer sistema numérico hipercomplejo: el conjunto  de los cuaterniones. Entusiasmado por su súbita inspiración, Hamilton cogió su navaja y talló en la piedra del puente el que es probablemente el graffiti matemático más célebre de la historia:
de los cuaterniones. Entusiasmado por su súbita inspiración, Hamilton cogió su navaja y talló en la piedra del puente el que es probablemente el graffiti matemático más célebre de la historia:

Cuando Hamilton fue a buscar su graffiti en el puente, quince años después, ya no fue capaz de volverlo a localizar. Pero en 1958, el entonces jefe del gobierno irlandés Éamon de Valera,[4] (1882-1975), inauguró, para regocijo de los turistas con aficiones matemáticas, una placa conmemorativa en el puente en la que se puede leer (todavía):
Mientras paseaba por aquí el 16 de octubre de 1843, Sir William Rowan Hamilton descubrió en un momento de genialidad la fórmula fundamental de la multiplicación de cuaterniones:y la grabó en una piedra del puente.

La placa que conmemora el descubrimiento de los cuaterniones, en el puente de Brougham (Wikimedia, CC BY-SA 2.0)
Los cuaterniones tienen por tanto cuatro componentes: una componente “real”, que Hamilton denominó parte escalar del cuaternión, y tres componentes ”imaginarias”, que Hamilton denominó parte vectorial del cuaternión. Un cuaternión 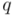 puede ser visto como la suma formal de un escalar y de un vector tridimensional:
puede ser visto como la suma formal de un escalar y de un vector tridimensional:

Donde 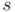 ,
,  ,
,  y
y  son números reales. La parte escalar de escalar de
son números reales. La parte escalar de escalar de 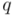 sería:
sería:

y la parte vectorial sería:

Como en total tiene cuatro componentes, el cuaternión es un objeto cuadridimensional, y no es posible representarlo en tres dimensiones. Si tenemos en cuenta que al principio Hamilton buscaba generalizar los complejos a tres dimensiones, podría parecer un inconveniente. Pero Hamilton no tardó en convencerse de que en el fondo era una ventaja de los cuaterniones sobre los complejos el hecho de que hubiera una parte escalar aparte de la parte vectorial tridimensional.
Las tres unidades  ,
,  y
y  se pueden interpretar como una base de vectores unitarios mutuamente perpendiculares[5] entre sí. La orientación de esta base se escoge de modo que sigue la convención de la regla de la mano derecha:[6] si colocamos la mano derecha extendida en dirección y sentido del vector
se pueden interpretar como una base de vectores unitarios mutuamente perpendiculares[5] entre sí. La orientación de esta base se escoge de modo que sigue la convención de la regla de la mano derecha:[6] si colocamos la mano derecha extendida en dirección y sentido del vector  , con la palma mirando según el sentido del vector
, con la palma mirando según el sentido del vector  , el pulgar extendido apunta en dirección del vector
, el pulgar extendido apunta en dirección del vector  .
.
En la figura que sigue se representa la base ortonormal de vectores  ,
,  y
y  con la orientación estándar. Si cambiáramos el sentido de un número impar de vectores (sólo uno o los tres), obtendríamos un sistema con orientación opuesta, que seguiría la regla de la mano izquierda. La imagen que resultaría de reflejar la figura en un espejo también correspondería a una sistema con orientación según la regla de la mano izquierda.
con la orientación estándar. Si cambiáramos el sentido de un número impar de vectores (sólo uno o los tres), obtendríamos un sistema con orientación opuesta, que seguiría la regla de la mano izquierda. La imagen que resultaría de reflejar la figura en un espejo también correspondería a una sistema con orientación según la regla de la mano izquierda.

Las unidades  ,
,  y
y  como base ortonormal de vectores del espacio tridimensional. El origen desde donde parten los tres vectores unitarios debe imaginarse más lejano para el observador que los extremos finales, marcados por las puntas de flecha.
como base ortonormal de vectores del espacio tridimensional. El origen desde donde parten los tres vectores unitarios debe imaginarse más lejano para el observador que los extremos finales, marcados por las puntas de flecha.
La suma de cuaterniones se define de forma análoga a la suma de números complejos, sumando cada componente (la real y las tres vectoriales) por separado. Sumemos, a modo de ejemplo, dos cuaterniones 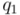 y
y  :
:




El producto de cuaterniones queda definido por las mismas propiedades del producto de complejos, excepto la conmutatividad, que sólo se exige cuando alguno de los factores es escalar, y por las reglas del producto de las unidades imaginarias  ,
,  y
y  . Multipliquemos los mismos cuaterniones
. Multipliquemos los mismos cuaterniones 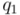 y
y  del ejemplo anterior. Ojo al orden de los productos, que es muy importante:
del ejemplo anterior. Ojo al orden de los productos, que es muy importante:





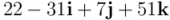
Si hubiésemos multiplicado en orden cambiado,  , hubiéramos obtenido un resultado diferente, como podéis comprobar por vuestra cuenta:
, hubiéramos obtenido un resultado diferente, como podéis comprobar por vuestra cuenta:

Lo que sí tienen en común ambos productos es que tienen la misma parte escalar (que no depende del orden de multiplicación) y la misma norma o módulo, concepto que definiremos dentro de muy poco.
Conjugado de un cuaternión
De forma análoga a los complejos, definimos el cuaternión conjugado de 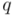 , que indicaremos
, que indicaremos  , como el cuaternión que tiene la misma parte escalar que
, como el cuaternión que tiene la misma parte escalar que 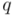 , y que su parte vectorial es la de misma de
, y que su parte vectorial es la de misma de 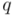 cambiada de signo:
cambiada de signo:


El producto de cualquier cuaternión 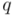 por su conjugado
por su conjugado  conmuta siempre (
conmuta siempre ( ) y da como resultado un número real, que no es más que la suma de los cuadrados de las cuatro componentes (
) y da como resultado un número real, que no es más que la suma de los cuadrados de las cuatro componentes (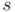 ,
,  ,
,  ,
,  ) del cuaternión:
) del cuaternión:





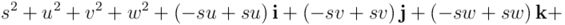


Si cambiamos de signo las partes vectoriales, estaríamos calculando el producto en orden invertido ( ). Como se ve, da lo mismo, ya que en el resultado final aparece la suma de los cuadrados de las componentes, que no varía al cambiar de signo
). Como se ve, da lo mismo, ya que en el resultado final aparece la suma de los cuadrados de las componentes, que no varía al cambiar de signo  ,
,  y
y  .
.
Norma o módulo de un cuaternión
La norma de un cuaternión es lo que intuitivamente entendemos como su ”longitud” en un espacio cuadridimensional. Indicaremos la norma de 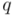 como
como  y su valor será la raíz cuadrada del producto del cuaternión por su conjugado:
y su valor será la raíz cuadrada del producto del cuaternión por su conjugado:
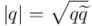
De lo visto en el apartado anterior, para  :
:

Inverso de un cuaternión no nulo
Podemos encontrar el inverso  de cualquier cuaternión
de cualquier cuaternión 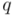 diferente de
diferente de  (naturalmente, entendemos por
(naturalmente, entendemos por  el cuaternión
el cuaternión  ) dividiendo su conjugado por el cuadrado de su norma, análogamente a como se obtiene en el caso de los números complejos:
) dividiendo su conjugado por el cuadrado de su norma, análogamente a como se obtiene en el caso de los números complejos:
 [7]
[7]
Efectivamente, tal como debe ser, se comprueba que es el inverso tanto por la derecha:
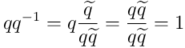
como por la izquierda:
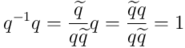
Los cuaterniones son un cuerpo no conmutativo
Veamos las propiedades de la suma de cuaterniones, que son análogas a las propiedades de la suma de complejos, que vimos ya en la correspondiente entrada:
1) La suma de cuaterniones es asociativa, con lo cual no es necesario especificar con paréntesis cómo se hace la suma de más de dos cuaterniones:
 para todo
para todo 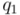 ,
,  ,
,  de
de 
2) Existe un elemento neutro de la suma de cuaterniones, que es el  , que sumado a cualquier cuaternión
, que sumado a cualquier cuaternión 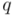 vuelve a dar
vuelve a dar 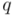 :
:
 para todo
para todo 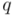 de
de 
3) Para todo cuaternión 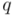 existe un cuaternión opuesto, que indicaremos como
existe un cuaternión opuesto, que indicaremos como  , y que sumado a
, y que sumado a 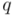 da el elemento neutro:
da el elemento neutro:
 para todo
para todo 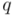 de
de 
4) La suma de cuaterniones es conmutativa:
 para todos los
para todos los 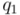 ,
,  de
de 
Todas estas propiedades definen a , el conjunto de los cuaterniones dotado de la operación suma, como un grupo conmutativo (o grupo abeliano).
, el conjunto de los cuaterniones dotado de la operación suma, como un grupo conmutativo (o grupo abeliano).
Veamos ahora las propiedades del producto de cuaterniones:
1) Es asociativo:
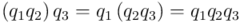 para todo
para todo 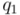 ,
,  ,
,  de
de 
2) Existe un elemento neutro del producto (llamado elemento unidad), que es el  , que multiplicado (tanto por la izquierda como por la derecha) por otro cuaternión
, que multiplicado (tanto por la izquierda como por la derecha) por otro cuaternión 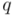 vuelve a dar
vuelve a dar 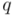 :
:
 para todo
para todo 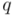 de
de 
3) Para todo cuaternión 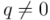 existe un cuaternión inverso, que indicaremos como
existe un cuaternión inverso, que indicaremos como  , y que multiplicado por
, y que multiplicado por 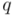 da el elemento unidad:
da el elemento unidad:
 para todo
para todo 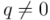 de
de 
Por tanto  , el conjunto de los cuaterniones, con exclusión del
, el conjunto de los cuaterniones, con exclusión del  , dotado de la operación producto, es un grupo no conmutativo, ya que, en general,
, dotado de la operación producto, es un grupo no conmutativo, ya que, en general, 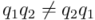 .
.
Finalmente, el producto de cuaterniones es distributivo respecto a la suma, tanto por la derecha como por la izquierda:
 , para todo
, para todo 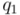 ,
,  ,
,  de
de 
 , para todo
, para todo 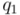 ,
,  ,
,  de
de 
La distributividad del producto, la estructura de  como grupo abeliano respecto a la suma de cuaterniones y la estructura de
como grupo abeliano respecto a la suma de cuaterniones y la estructura de  como grupo respecto al producto, definen a
como grupo respecto al producto, definen a  , el conjunto de los cuaterniones dotado de las operaciones suma y producto, como un cuerpo no conmutativo, también llamado cuerpo asimétrico, o incluso, para los puristas que exigen la conmutatividad del producto para poder hablar de cuerpo propiamente dicho, un anillo de división.[8]
, el conjunto de los cuaterniones dotado de las operaciones suma y producto, como un cuerpo no conmutativo, también llamado cuerpo asimétrico, o incluso, para los puristas que exigen la conmutatividad del producto para poder hablar de cuerpo propiamente dicho, un anillo de división.[8]
El propio Hamilton fue víctima de la fascinación que le produjeron los cuaterniones: a partir de aquel 16 de octubre de 1843 y hasta su muerte dedicó toda su actividad a investigar y dar a conocer su nuevo descubrimiento, al que dio tanta importancia “como la que tuvo el descubrimiento de las fluxiones [por Newton] en el siglo XVII”.[9] Y efectivamente, los cuaterniones encontraron pronto aplicaciones en la Física: cuando James Clerk Maxwell descubrió sus célebres ecuaciones que unificaban los fenómenos electromagnéticos y lumínicos y a las que Pedro dedicó una serie, pronto las expresó en el lenguaje de los cuaterniones. En el próxima entrada veremos cómo los dos productos de vectores que seguramente conocéis, el producto escalar y el producto vectorial, se derivan del producto de cuaterniones.
-
A los trece años Hamilton conocía tantas lenguas como años tenía: no sólo lenguas europeas modernas, sino también latín, griego clásico, árabe, sánscrito o persa, pero ya a los 8 años, tras ser derrotado por otro niño prodigio americano en una competición de cálculos matemáticos, había decidido dedicar más tiempo a las matemáticas que a las lenguas, que pasaron a ser desde entonces para él una actividad secundaria, para “relajarse” y desconectar de sus actividades serias… [↩]
-
Ya hacia 1830 había ensayado una generalización de los complejos a tres dimensiones, en la que los complejos generalizados se representaban en coordenadas esféricas, y el módulo del producto era el producto de módulos, el ángulo polar (o colatitud) del producto era la suma de ángulos polares, y el ángulo azimutal (o longitud) era la suma de ángulos azimutales: un producto que ni siquiera era distributivo respecto a la suma… [↩]
-
Como veis, he decidido poner en negrita las unidades imaginarias. No es la elección habitual, tratándose de cuaterniones, pero creo que hace la lectura más fácil y es más sugerente para los que ya conozcáis la notación del álgebra vectorial tradicional. [↩]
-
De Valera, además de ser una de las figuras políticas más importantes y controvertidas de la historia de Irlanda, fue matemático y estudió en profundidad los cuaterniones, por los que sentía una predilección especial. Según el propio de Valera, en 1916, mientras esperaba su fusilamiento junto a otros participantes en un alzamiento fracasado contra la corona británica (fusilamiento del que se salvó gracias, al menos en parte, al hecho de disponer de pasaporte estadounidense) reprodujo en la pared de su celda el graffiti de Hamilton, como homenaje a la aportación más famosa a las matemáticas de un irlandés. Este graffiti de de Valera tampoco se conserva, por lo que creo recordar. [↩]
-
O, como se dice más técnicamente, ortogonales. Una base de vectores unitarios y mutuamente ortogonales se dice que es una base ortonormal. [↩]
-
Que es, por cierto, la opuesta de la que seguía Hamilton, la regla de la mano izquierda. [↩]
-
Es posible expresar
 en forma de fracción debido a que en el denominador tenemos
en forma de fracción debido a que en el denominador tenemos  , que es un número real, y cuyo inverso es también real y conmuta con cualquier cosa. Pero en general, para dividir dos cuaterniones arbitrarios
, que es un número real, y cuyo inverso es también real y conmuta con cualquier cosa. Pero en general, para dividir dos cuaterniones arbitrarios  y
y 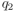 , hay que elegir entre postdividir, haciendo
, hay que elegir entre postdividir, haciendo 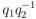 , o bien predividir, haciendo
, o bien predividir, haciendo  , ya que el orden del producto importa y en general no tiene sentido escribir cosas como
, ya que el orden del producto importa y en general no tiene sentido escribir cosas como  , en donde no queda claro el orden en que se multiplica por el inverso. [↩]
, en donde no queda claro el orden en que se multiplica por el inverso. [↩] -
Un anillo es la estructura algebraica que tiene un conjunto que tiene estructura de grupo aditivo abeliano (suma asociativa, con elemento neutro y elemento opuesto), estructura de semigrupo multiplicativo (sólo asociatividad del producto), y la multiplicación es distributiva respecto a la suma por los dos lados. Si además existe elemento neutro de la multiplicación distinto del neutro de la suma, se dice que el anillo es unitario. Si además, todo elemento distinto de 0 es invertible, el anillo unitario pasa a anillo de división, y sólo le falta la conmutatividad del producto para ser declarado cuerpo propiamente dicho. [↩]
-
No deja de ser una lástima, porque las aportaciones de Hamilton al tema de los cuaterniones de ahí en adelante no fueron tan significativas como las que hizo en otros terrenos, como en la mecánica clásica o la óptica. [↩]

The Explorando el álgebra geométrica 3 – Antecedentes – Los cuaterniones (I) by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.




{ 1 } Comentarios
Muy buena entrada divulgativa.
Escribe un comentario