El Cedazo

Esta nueva entrada de la serie dedicada al álgebra geométrica trata del álgebra del plano euclídeo, . Como sabemos desde la entrada 10 de la serie, esta álgebra tiene como espacio lineal un total de 4 dimensiones: los objetos de tienen una componente escalar, dos vectoriales y una bivectorial. Vamos a ver que la parte de grado par (escalares y bivectores) tiene especial importancia: para empezar forma una subálgebra dentro de (si sumamos y multiplicamos entre sí objetos de grado par siempre obtendremos objetos de grado par), y además se puede reconocer fácilmente en ella algo que ya conocemos: los números complejos. Veremos que los complejos, que forman la subálgebra par de , actúan como operadores de rotación-reescalado sobre los vectores.

Un multivector de es, como sabemos, un objeto cuadridimensional: tiene una componente escalar, dos componentes vectoriales y una componente bivectorial.

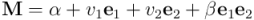
Podemos comenzar a distinguir entre una parte de grado par y una parte de grado impar. El número de dimensiones de grado par (2) es igual al número de dimensiones de grado impar, como sucede en cualquier álgebra geométrica. Los elementos de que sólo tienen partes de grado par forman una subálgebra: si multiplico entre sí dos multivectores que sólo tienen partes de grado par, vuelvo a obtener un multivector con sólo partes de grado par. En cambio, la parte de que sólo contiene multivectores de grado impar (y en este caso, formada en exclusiva por los vectores) no es una subálgebra: si multiplico dos vectores obtengo una suma de escalar más bivector, que es par, con lo que me salgo del conjunto de multivectores de grado impar.

Si nos fijamos un poco veremos que la subálgebra par de es algo muy familiar. Llamemos a la unidad pseudoescalar de , el bivector :

Si calculamos el cuadrado de multiplicándolo por sí mismo obtenemos:

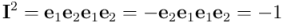
Por tanto, en  tenemos que , y vemos que se comporta igual que , la unidad imaginaria de los números complejos. Además, conmuta con los números reales, igual que la unidad imaginaria . Dos multivectores pertenecientes a la subálgebra par de  se suman y multiplican entre ellos exactamente igual que dos números complejos:

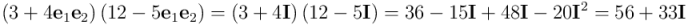
El comportamiento de los elementos de la subálgebra par al operarlos entre sí es absolutamente indistinguible del que tienen los números complejos, y por ello a los matemáticos les gusta decir que la subálgebra par de y el conjunto de los números complejos son conjuntos isomorfos. Todo lo que sabemos sobre números complejos es aplicable a la subálgebra par de . Por ejemplo, como el producto de números complejos es conmutativo, el producto de dos elementos de la subálgebra par también lo será. También podemos expresar cualquier elemento de la subálgebra par en forma polar, como los complejos:

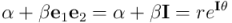
Donde, de forma totalmente análoga a como vimos en la correspondiente entrada dedicada a los números complejos, es el módulo del “complejo”:

y el ángulo es su correspondiente argumento:

En la práctica, nos podemos referir tranquilamente a los elementos de la subálgebra par de como “complejos”.

La reversión hace el papel de la conjugación compleja

Como el reverso de es igual a :

tenemos que la conjugación compleja, desde el punto de vista del álgebra geométrica, no es más que la reversión:

La diferencia entre e es que tiene una interpretación geométrica directa, al ser la unidad pseudoescalar de , una superficie unitaria orientada, mientras que es simplemente una abstracta raíz cuadrada de la unidad negativa sin relación con la geometría. Además puede multiplicarse perfectamente por un vector, para dar, como veremos, el vector rotado en 90º, mientras que un producto de por un vector no tiene sentido geométrico.

El producto de vectores y bivectores de anticonmuta

El producto de , la unidad pseudoescalar de , por un vector anticonmuta: el resultado de la multiplicación cambia de signo al cambiar el orden del producto:

Una forma muy sencilla de verlo, aunque no muy elegante que digamos, es comprobar que anticonmuta tanto con como con , los vectores de la base ortonormal en que estemos trabajando:

Comprobémoslo primero con el vector :

Y a continuación con el vector :

Y claro, como cualquier vector se puede expresar como combinación lineal de los vectores y y todo bivector de es múltiplo escalar de , se deduce que los vectores del plano anticonmutan con los pseudoescalares de .

Este modo de demostrar la anticonmutatividad del producto de un vector por la unidad pseudoescalar en no es elegante porque procede componente a componente. Imaginad que tuviéramos que comprobar si un vector de conmuta o anticonmuta con el correspondiente pseudoescalar unitario comprobándolo para cada vector de la base ortonormal: sería patético.

Una idea pedagógica sobre la que se insiste mucho en álgebra geométrica es que trabajar componente a componente sin necesidad es un caso flagrante de coordinitis,^[1] un síntoma de una gran limitación de la capacidad conceptual. Es como empeñarse en usar unas muletas para caminar cuando no se necesitan.

Pero pensando geométricamente, sin atarnos a la idea de que un vector es una combinación lineal de los vectores de una particular base ortonormal, podemos demostrar que anticonmuta con cualquier vector de un modo más directo:

La unidad pseudoescalar de es pero se puede reexpresar siempre como , donde el vector es un vector ortogonal al vector , de modo que el área del paralelogramo de lados y valga 1 y su orientación sea la misma que la del cuadrado orientado .

En la figura tenemos un mismo bivector, , expresado de dos formas diferentes. Recordemos que dos superficies orientadas iguales y con la misma orientación representan el mismo bivector. Podemos elegir una forma u otra según nos convenga mejor a la hora de hacer un cálculo o razonamiento en álgebra geométrica.

Tendremos entonces:

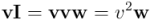
Y si multiplicamos en orden inverso:

Donde hemos utilizado el hecho de que los vectores y son ortogonales y, por tanto, anticonmutan. En dimensiones superiores a 2, y para ello serviría básicamente la misma demostración, también se cumple que los bivectores simples anticonmutan con los vectores contenidos en el mismo plano (o en un plano paralelo) que el del bivector.

Además, como el área del paralelogramo de lados y vale 1, se cumple y tendremos entonces:

Es decir, obtenemos un vector con la misma norma de , pero que apunta en la dirección de . Del mismo modo:

Es decir, el efecto de multiplicar un vector del plano por es rotar el vector 90º en el mismo sentido de rotación que va desde a , cuando multiplica por la derecha, o 90º en el sentido contrario, cuando multiplica por la izquierda.^[2] En esta misma entrada veremos qué hay que hacer para rotar un vector un ángulo diferente de 90º.

El producto geométrico de dos vectores de como complejo

Volvamos una vez más a la fórmula fundamental del producto geométrico de dos vectores:

El producto geométrico de dos vectores de es la suma de un escalar y de un bivector y, por tanto, se puede interpretar como un número complejo. Recordemos, además, que el producto interior de dos vectores es igual al producto de las normas de los vectores por el coseno del ángulo que forman:

También vimos que la norma del producto exterior de dos vectores es igual al producto de las normas de los vectores por el módulo del seno del ángulo que forman:

No cuesta mucho ver que en  el producto exterior de dos vectores se puede escribir como:

Efectivamente, en todo bivector es múltiplo del pseudoescalar unitario , y el signo del seno será positivo o negativo según el sentido del bivector sea igual u opuesto al bivector . Como es costumbre representar en el plano los ángulos positivos como los que van contra el sentido de las agujas del reloj, represento en las figuras al pseudoescalar unitario como un cuadrado en el que el ángulo recto que va de a  se recorre en sentido contrario a las agujas del reloj, aunque el álgebra geométrica por sí misma no necesita establecer ningún tipo de convenio de sentido para los multivectores.

O sea, podemos escribir el producto de dos vectores como:

Y obtenemos el producto de las normas de los dos vectores por un complejo unitario cuyo argumento es el ángulo , cuyo sentido se toma del primer vector que se multiplica, en este caso , al segundo, en este caso .

El producto geométrico de dos vectores de es un complejo cuyo módulo es el producto de las normas de los vectores y cuyo argumento es el ángulo relativo que forman los dos vectores entre sí. El sentido de este ángulo relativo va siempre del primer vector que se multiplica hacia el segundo vector.

Como el resultado del producto geométrico sólo depende de las normas de los vectores y del ángulo relativo formado entre ellos, su valor no cambia si se rota un mismo ángulo cada uno de los vectores. En dimensiones mayores que 2 esto también es cierto, siempre que la rotación de ambos vectores los mantenga en el mismo plano en que se encuentren originalmente.

Como el valor del producto geométrico de dos vectores de sólo depende de las normas de los vectores del ángulo relativo 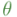que forman, su valor no cambia al aplicar a ambos una misma rotación de ángulo .

Todo complejo de puede imaginarse también como producto de dos vectores elegidos de modo que el producto de sus normas dé la norma del complejo y que el ángulo relativo entre ellos sea el argumento del complejo.

Un vector de tiene una “orientación absoluta” en el plano, mientras que el argumento de un complejo representa una “orientación relativa” entre dos vectores del plano. Si el producto de dos vectores da un complejo, el producto de dos complejos es, como vimos en la correspondiente entrada, otro complejo cuya norma es también el producto de las normas de los complejos que se multiplican, pero el argumento ya no es el ángulo relativo, como en el producto de vectores, sino la suma de argumentos de los complejos. Esta suma de argumentos representa una suma de rotaciones relativas, lo cual nos lleva al apartado siguiente…

Los complejos unitarios como operadores de rotación

La deducción general de cómo se rota un vector en una álgebra geométrica cualquiera aún tiene que esperar algunas entradas, pero para el caso bidimensional ya podemos verificar este importante resultado:

Para rotar un vector de un ángulo , hay que multiplicarlo por la derecha por el complejo unitario :

Donde el vector 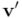es el resultado de la rotación.

Para rotar un vector un ángulo hay que multiplicarlo por complejo unitario 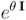por la derecha. También se obtiene el mismo resultado multiplicando por el conjugado del complejo anterior por la izquierda. Incluso, se puede obtener la rotación multiplicando el vector por por la izquierda y por por la derecha. De hecho, esta última fórmula es la válida cuando se generaliza la fórmula de rotación a más dimensiones.

Consideremos un vector cualquiera de , , y el vector resultante de rotar un ángulo , que denominaremos 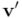. El producto 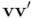será, como sabemos:

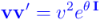
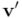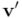Ya que tanto como tienen la misma norma, . Para despejar multiplicamos por la izquierda a ambos lados de la igualdad por el inverso de , que, como sabemos, es , y tendremos:

El complejo es función únicamente del ángulo de rotación, y por tanto vale para cualquier vector de que queramos rotar.

Por otro lado, también podíamos haber partido de la reversión del producto de vectores :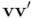

Como el producto ha cambiado de orden, el ángulo relativo cambia de signo. Para despejar ahora 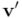hay que multiplicar ambos lados de la ecuación por el inverso de , pero por la derecha. El resultado final es:

Es decir, podemos rotar un vector un ángulo bien multiplicándolo por la derecha por el complejo de norma unidad 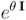, o bien multiplicándolo por la izquierda por el respectivo complejo unitario conjugado .

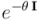También podíamos haber deducido fácilmente esta segunda fórmula para la rotación de un vector a partir de la primera, aplicando la propiedad de que los vectores conmutan con la parte escalar de los complejos, pero anticonmutan con la parte pseudoescalar (recordemos: ).

Incluso podríamos intentar rizar el rizo y “repartir” la rotación por los dos lados, haciendo “media rotación” multiplicando por la izquierda y “la otra media” multiplicando por la derecha:

Esta forma parece más artificiosa, y de hecho es más complicada de calcular por incluir más multiplicaciones, pero, curiosamente, a la hora de generalizar la fórmula de la rotación de un vector a dimensiones superiores a 2 es el único modo correcto de proceder: veremos que para rotar un vector en espacios de dimensión superior a dos hay que colocar el vector como ingrediente central de un “sandwich multiplicativo” entre dos exponenciales de un bivector, una inversa de la otra.

El diagrama de Argand según el punto de vista del álgebra geométrica

En podemos hacer una correspondencia uno a uno entre los vectores del plano y los complejos: si partimos de un vector  y lo multiplicamos por la izquierda por un vector unitario, que denominaremos (y que escogeremos como primer vector de nuestra base ortonormal), el resultado será un complejo:

Y a partir de cualquier complejo podemos recuperar el vector de partida asociado multiplicando por por la derecha:

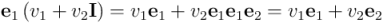
Podemos interpretar el complejo 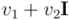como un operador de rotación-reescalado que transforma el vector unitario rotándolo un ángulo igual al argumento del complejo y multiplicando su norma por la norma del complejo para producir el vector .

El álgebra geométrica hace visible el hecho de que en el plano de Argand los complejos se están representando mediante vectores. Al complejo a representar, 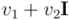, se lo premultiplica por un vector unitario , que dará la dirección que se escoge como “eje real”. El resultado de este producto será un vector, , que representará en el plano al complejo que codifica la rotación-reescalado que transforma en , mediante una rotación de ángulo (igual al argumento del complejo) y un reescalado consistente en multiplicar la norma de (que vale 1) por la norma del complejo. El vector representará a , la unidad imaginaria.

Esta correspondencia entre vectores y complejos es lo que permite representar a los complejos en el llamado plano de Argand, que ya vimos en la segunda entrada dedicada a los complejos.

Aplicación a la Física: la ley de Ohm en corriente alterna

Acabo la entrada con un ejemplo, sacado de la Física, de la distinción que hace el álgebra geométrica entre vectores y complejos: la ley de Ohm de la corriente alterna. Una tensión alterna, 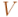, que oscila sinusoidalmente con el tiempo, puede ser imaginada como la proyección escalar sobre un eje de un vector 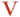que va rotando en el tiempo con la frecuencia de la corriente alterna. Del mismo modo, la intensidad alterna que recorre el circuito al que se le aplica la tensión se puede imaginar como la proyección escalar sobre el mismo eje de un vector intensidad, que gira a la misma velocidad angular, pero con un desfase respecto al vector .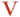

Una tensión alterna 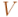se modeliza como la proyección escalar sobre un eje (por ejemplo, el vertical, como en la figura) de un vector tensión, 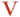que va girando con la frecuencia alterna. En el ejemplo de la figura, el vector tensión tiene un módulo de 220, correspondiente al valor máximo que puede tener la tensión, y una frecuencia de 50 vueltas/segundo (en frecuencia angular, 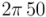radianes/s). La intensidad alterna, se puede ver también como la correspondiente proyección escalar de un vector intensidad que rota a idéntica frecuencia angular que el vector tensión. En la figura, la intensidad máxima tiene un valor de 22 y tiene un desfase constante respecto a la tensión aplicada de (60º). La impedancia, , es el factor complejo (para una frecuencia dada, depende de las características del circuito en que se aplica la tensión alterna) que multiplicado por la derecha del vector intensidad da el vector tensión. En el caso de la figura, se deduce que . Las gráficas de la tensión y de la intensidad respecto al tiempo están en la próxima figura.

La ley de Ohm de la corriente alterna dice que el vector tensión es igual al vector intensidad multiplicado (en este orden) por una impedancia, que hace el papel de “resistencia compleja” (la impedancia es el resultado, dependiente también de la frecuencia alterna aplicada, de la combinación, sea en serie o paralelo, de las resistencias, capacitancias e inductancias que haya en el circuito). El modo correcto de representar tensión e intensidad es como vectores, por tener estos una “fase absoluta”. La impedancia, cuya fase es, precisamente, el desfase relativo entre tensión e intensidad, es un valor complejo. Como el uso del álgebra geométrica no está estandarizado en los planes de estudio, lo habitual es representar todo mediante complejos, lo que no es relevante de cara a los cálculos prácticos, pero no es  conceptualmente correcto.

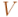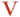En la gráfica se representan como función del tiempo los valores de la tensión y la intensidad , que son la proyección escalar sobre el eje vertical de los respectivos vectores y . Las proyecciones escalares son las magnitudes que realmente tienen sentido físico. Los valores son los del ejemplo propuesto en la figura anterior. Se puede observar que la intensidad va desfasada (en 60º) respecto a la tensión.

1. El mérito de la invención de la expresión corresponde a David Hestenes, el principal impulsor del álgebra geométrica, que la introdujo en un artículo titulado Mathematical Viruses. [↩]

2. Normalmente se escoge en el plano como sentido positivo de rotación el sentido contrario a las agujas del reloj, y como negativo el sentido horario. Por eso, en la figura he indicado tanto el sentido de giro desde el vector al , como respectivamente el que va desde a 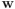, como antihorario. [↩]

The Explorando el álgebra geométrica 12 – El álgebra geométrica del plano euclídeo by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.