El Cedazo

En la entrada anterior terminamos la introducción histórica al álgebra geométrica; con esta entrada de hoy daremos por fin nuestros primeros pasos en el álgebra geométrica. Presentaré los axiomas, las reglas del juego del álgebra geométrica. Los vectores, entendidos geométricamente como “segmentos lineales orientados”, serán los generadores del álgebra, es decir, cualquier elemento de un álgebra geométrica se puede formar a partir de sumas y productos de vectores. Los números reales serán también elementos del álgebra. Una de las propiedades más interesantes de los cuaterniones era la asociatividad del producto y, por tanto, será uno de los axiomas que elijamos. Habrá otros axiomas que expresen las propiedades de linealidad y, finalmente, el axioma de contracción, el que da a las álgebras de Clifford su característica distintiva respecto a otras álgebras asociativas. A partir de los axiomas, comenzaremos a analizar el producto de dos vectores para posteriormente establecer las relaciones con la geometría.

Los vectores del espacio vectorial los representamos con letras minúsculas del alfabeto latino en negrita: , , … …^[1]

Todos los vectores de pertenecen también al álgebra , así como todos las sumas y productos que se puedan obtener a partir de ellos. Los números reales también pertenecen al álgebra, nos referiremos a ellos como escalares y los representaré preferentemente con letras griegas minúsculas: , , …, … 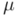Los elementos genéricos del álgebra , que llamaremos multivectores, serán representados con letras mayúsculas (sin negrita) del alfabeto latino: , , …^[2]

Partimos, pues, de un espacio vectorial de 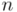dimensiones, . Recordemos antes las propiedades que definen un espacio vectorial, o también espacio lineal, que podemos dividir en dos grupos:

Espacio vectorial: propiedades de la suma de vectores

En un espacio vectorial se define la suma como una operacion interna (ya que tanto los sumandos como el resultado son vectores) con las siguientes propiedades:

1) Conmutatividad:

Para todo , de se cumple:

2) Asociatividad:

Para todo , , de se cumple:

3) Existe un elemento neutro de la suma de vectores:

Este elemento neutro lo indico simplemente como , no como , adelantándome al hecho de que los vectores estarán también incluidos junto a los números reales en el álgebra . En álgebra geométrica no tiene sentido distinguir entre escalar y   vector. El elemento neutro, el , es único para toda el álgebra, y es a la vez escalar, vector, o cualquier tipo de multivector que haga falta.

4) Todo vector tiene su opuesto , que cumple:

Espacio vectorial: propiedades del producto de un escalar por un vector

En un espacio vectorial se define también una operación externa,^[3] el producto de un escalar por un vector que da como resultado un vector. Las propiedades de este producto de escalares por vectores son:

1) Asociatividad. Si y son escalares y es un vector, siempre se cumplirá:

Dentro del primer paréntesis, el producto es el producto ordinario de números reales. El resto de productos que aparecen después son todos ejemplos del producto externo de escalares por vectores.

2) El elemento unidad, , de los escalares se comporta como neutro multiplicativo:

, para todo de

3) El producto de escalares por vectores es distributivo respecto a la suma de escalares:

Para todo y pertenecientes a  y para todo perteneciente a :

4) El producto de escalares por vectores es distributivo respecto a la suma de vectores:

Para todo  perteneciente a y para todo  y pertenecientes a :

Axiomas del álgebra geométrica

Los elementos de este espacio vectorial, o vectores, los interpretaremos geométricamente como segmentos lineales orientados sin que importe para su distinción el punto de origen o aplicación, lo que en Física se conoce como vectores libres. A partir de ellos construimos, mediante productos y sumas, el resto de objetos del álgebra geométrica. Un sistema de axiomas definirá de forma implícita un producto geométrico entre cualquier par de elementos del álgebra, llamado también producto de Clifford,^[4] que abarca tanto los productos ordinarios de números reales entre sí como los productos de reales por vectores y que se generaliza a todos los tipos de elementos del álgebra. Por otra parte, la operación suma  también se generaliza de forma trivial, extendiéndose a la suma de cualquier tipo de multivector.

Axioma 0. Todos los vectores de son también elementos del álgebra geométrica y además generan, a partir de todas las combinaciones de sumas y productos entre ellos, cualquier elemento de . La suma de multivectores, que es como  denominaremos los elementos genéricos de , es conmutativa y asociativa, como la suma de vectores:

Para todo par de elementos cualquiera, , del álgebra :

(Conmutatividad de la suma de multivectores)

Para todo , , de :

(Asociatividad de la suma de multivectores)

Axioma 1. El producto geométrico de elementos de  será asociativo y, por tanto, no será preciso especificar la posición de los paréntesis en un producto geométrico con tres (o más) factores.

Para todo , y de se cumple:

Axioma 2. Distributividad del producto geométrico respecto a la suma, tanto por la izquierda como por la derecha. Para todo , y de se cumplirá:

Axioma 3. Los escalares, que en álgebra geométrica son siempre los números reales,^[5] conmutan con cualquier elemento de . Para todo de y cualquier de se cumplirá:

Como los escalares también pertenecen al álgebra ,^[6] el producto de un escalar por un multivector de  ya no se considera una ley de composición externa, como es el caso de un espacio vectorial cualquiera. Por ello tiene sentido preguntarse si el producto de un real por un multivector conmuta o no. Pues bien, por el axioma 3 exigimos la conmutatividad del producto geométrico de un real por cualquier elemento de . No se exige, sin embargo, la conmutatividad del producto de un par de multivectores cualesquiera, y en general tendremos que .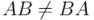

Axioma 4. El número real será el elemento neutro del producto geométrico.

Para todo perteneciente a tenemos:

Axioma 5 (axioma de contracción). El cuadrado geométrico de cualquier vector diferente de será siempre un escalar, un número real. Para todo de :

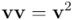pertenece a

Axioma 5b. Además de real, el cuadrado de cualquier vector diferente de , es siempre un número positivo:

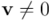para todo de

No es estrictamente necesario que se cumpla el axioma 5b para tener una álgebra geométrica. Por ejemplo, en el álgebra geométrica de la relatividad especial hay vectores distintos de con cuadrado positivo, negativo, e incluso . Pero de momento, para las álgebras asociadas a espacios de métrica euclídea, exigiremos que todo vector distinto de tenga cuadrado positivo. De hecho 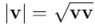 será lo que nos de de la norma del vector , que es lo que intuitivamente entendemos como su longitud, y, claro, no nos podemos permitir que dentro de la raíz cuadrada aparezca un número negativo…

El axioma de contracción implica además que el producto geométrico de dos vectores colineales, uno de los cuales resulta de multiplicar el otro por un escalar, es también un número real:

Donde se han aplicado sucesivamente los axiomas 1 (asociatividad del producto), 3 (conmutatividad del producto por escalares), otra vez asociatividad del producto, y finalmente el axioma de contracción. De hecho, podríamos haber tomado sin ningún problema como axioma de contracción que el producto de dos vectores colineales es siempre real.

Más adelante veremos que como consecuencia de los axiomas la misma álgebra geométrica tiene también estructura de espacio vectorial. Si la dimensión del espacio vectorial base, , es 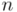, veremos en otra entrada que la dimensión de como espacio vectorial es . Claro está que los elementos de ya no pueden ser considerados “vectores como flechas orientadas”, sino vectores en sentido abstracto (“aquello que verifica las propiedades que definen implícitamente los vectores en un espacio vectorial”), como puede ser, por ejemplo, tripletas ordenadas de números reales, matrices de 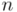filas y  columnas de números complejos, etc. Por eso, en álgebra geométrica se suele evitar la expresión espacio vectorial y se prefiere decir espacio lineal, para evitar la ambigüedad de hablar de vectores en sentido físico estricto (segmentos unidimensionales orientados), o de “vectores” en sentido de elementos que cumplen con una estructura matemática abstracta.

Descomposición del producto geométrico de dos vectores en dos partes

Veamos ahora qué podemos decir del producto geométrico de dos vectores como consecuencia de los axiomas.

Escribamos el producto geométrico de los vectores y  como suma de dos partes, una simétrica, que no cambia al intercambiar con , y otra antisimétrica, que sí cambia de signo al intercambiar y :

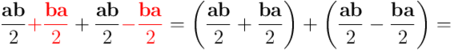
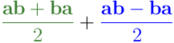
En la primera línea simplemente he escrito  como suma de dos mitades. Después he sumado y restado un mismo objeto, escogido astutamente, que he indicado en rojo. A continuación he agrupado todo como suma de dos paréntesis, el primero de los cuales es la parte simétrica de , ya que, como se puede observar, al intercambiar  con , se obtiene lo mismo, y el segundo es la parte antisimétrica de , ya que al intercambiar con , la expresión entre paréntesis cambia de signo. El primer  paréntesis aparece al final como el término escrito en verde, y el segundo, como término escrito en azul.

Fijémonos ahora en el primer término, en verde, en la parte simétrica del producto geométrico de los vectores y . La denominaremos producto interior de los vectores y y lo indicaremos como . Como estamos ante un resultado fundamental del álgebra geométrica lo resalto con fondo amarillo: Así pues:

El segundo término de la descomposición, en azul, es la parte antisimétrica del producto geométrico de los vectores y . La denominaremos producto exterior de los vectores y y lo indicaremos como . Así pues:

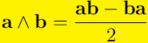
Por tanto, hemos descompuesto el producto geométrico de dos vectores en la suma de su producto interior más su producto exterior:

La simetría del producto interior de dos vectores se expresa así:

La antisimetría del producto exterior de dos vectores se expresa así:

Se deduce inmediatamente que el producto exterior de un vector por sí mismo es :

Y por tanto el cuadrado de cualquier vector (el producto geométrico de un vector por sí mismo) es siempre igual al producto interior del vector por sí mismo:

Antes de acabar por hoy, vamos a utilizar los axiomas para demostrar que el resultado del producto interior de vectores es un escalar. Ya en la próxima entrada veremos que coincide con el producto escalar de Heaviside-Gibbs, el que se utiliza en el álgebra vectorial ordinaria.

Del producto exterior diré de momento que no es el producto vectorial de Heaviside-Gibbs, aunque está muy relacionado. El producto vectorial lo indicaré, como he hecho hasta aquí, como se ve en la mayoría de los textos actuales y como ya hacía Gibbs, con el símbolo , y el producto exterior con el símbolo . Hay textos donde se usa el símbolo de producto exterior para indicar en realidad el producto vectorial, así que ¡cuidado con las confusiones!

El producto interior de dos vectores es siempre un escalar

A partir de nuestros axiomas, demostremos esta afirmación. Para ello, calculemos el cuadrado de la suma de los vectores y , y veremos cómo aparece el producto escalar que acabamos de definir:

He señalado en rojo dos términos del desarrollo que resultan ser el doble del producto interior . Ya está, de ahí puedo aislar el producto interior en función de cuadrados de vectores, pasando al otro lado de la igualdad, cambiados de signo, los términos al cuadrado que lo acompañan:

¿Qué vemos en la última línea? Que el producto interior  es igual a la mitad del cuadrado del vector  menos la mitad del cuadrado del vector y menos la mitad del cuadrado del vector . Pero el cuadrado de un vector, por el axioma 5, es siempre un escalar. Por tanto será siempre un escalar, un número real.

Estamos ya a punto de poder ver la interpretación geométrica del producto interior de vectores, pero eso debe ya quedar para la siguiente entrada, para no alargarnos demasiado. Veremos cómo con el producto interior podemos calcular longitudes de vectores y los ángulos que forman entre ellos.

1. En entradas posteriores, sobre todo al tratar de Física, relajaré la convención y me permitiré utilizar alguna letra mayúscula en negrita para algún vector, por ejemplo el del campo eléctrico , como es tradicional. [↩]

2. Este uso de los tipos de letras (minúsculas griegas para escalares, minúsculas latinas para vectores y mayúsculas para multivectores genéricos) se remonta a Graßmann. Sólo he añadido la negrita para los vectores, cosa que me permitirá usar minúsculas sin negrita para indicar la norma del vector correspondiente, según es costumbre entre físicos e ingenieros. [↩]

3. El primer factor no es un vector, sino un escalar, el segundo factor sí es un vector, por eso hablamos de operación externa. [↩]

4. El propio Clifford propuso la denominación de producto geométrico, que es la que se prefiere en álgebra geométrica. De hecho, fue Graßmann el primero en escribir el producto geométrico de dos vectores, hacia el final de su Ausdehnungslehre de 1862, aunque Clifford fuera el primero en reconocer su importancia. [↩]

5. También se podría construir una álgebra sobre otro cuerpo de escalares, como los números complejos, pero con ello ya no hablaríamos de álgebra geométrica, sino de simplemente de “álgebra de Clifford”. Para tener una interpretación geométrica de los multivectores del álgebra es esencial que los escalares sean reales. [↩]

6. Esto se deduce del axioma 0 y del axioma 5, que veremos después. [↩]

The Explorando el álgebra geométrica 7 – Los axiomas del álgebra geométrica by Juan Leseduarte, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.