(Revisión 2025)
En la entrada anterior de esta miniserie enfocamos al Universo como un sencillo cuerpo físico aislado al que se le puede aplicar una teoría básica que defina los condicionantes más generales en la evolución de su estado. Hablamos precisamente de su ecuación de estado y de cómo varía en su interior la densidad de materia/energía a lo largo de su proceso expansivo. Seguimos ahora en esta entrada con algo más de teoría a la sombra de una tercera ecuación fundamental que vamos a necesitar para analizar realmente cómo van a evolucionar los posibles caminos del Universo en su futuro. La vida dinámica del Universo queda reflejada por las ecuaciones de la relatividad general. En particular, la solución planteada por las ecuaciones de Friedman, que en su conjunto son utilizadas en cosmología física y que describen la expansión del Universo bajo la hipótesis de que es homogéneo e isótropo. En particular analizaremos la primera de sus ecuaciones:
en donde ρ es la densidad de materia/energía en el Universo -incluye también el efecto de la presión interna del sistema-, Λ que es la constante cosmológica[1] y k la curvatura espacio/temporal.
Vamos a razonar un poco con lo que nos dice a simple vista la ecuación y veamos a donde nos lleva. Hagamos primero un sencillo ejercicio de imaginación con el término intermedio donde aparece el factor de escala a.[2] Vamos a multiplicar numerador y denominador por X, siendo X una distancia entre dos puntos cualquiera del Universo. Con eso en mente nos podemos dar cuenta de que ese término imaginado es el cuadrado de la velocidad con que varía el segmento cósmico X, dividido por el propio segmento X; es decir, la velocidad con que se separan los extremos de X dividido por la distancia entre esos dos puntos: efectivamente, como anuncia la ecuación, se trata del cuadrado de la constante de Hubble. Vemos pues un primer fruto indispensable para nuestro propósito: usando las ecuaciones de Friedman podremos calcular cómo se expande el universo en función del tiempo.
Miremos ahora a la derecha de la igualdad. El primer término representa la lucha entre la materia/energía y la constante cosmológica, la energía oscura. La dinámica de la expansión del Universo depende del valor de la densidad ρ de su materia/energía y del valor de la constante cosmológica Λ. Con sus efectos gravitatorios opuestos, la primera favorece la compactación mientras que la segunda ayuda a lo contrario. ¿Quién ganará? En el momento actual parece que el pulso se lo está llevando la energía oscura Λ, aunque no fue así con anterioridad.[3]
Pero asimismo podemos ver en la ecuación de Friedmann que esa batalla también se ve modificada por el efecto de la curvatura k del Universo.Para un mismo inventario energético no sería lo mismo ver como crece/decrece un mundo cerrado en sí mismo siguiendo una geometría esférica, o un mundo de geometría plana o uno abierto en forma de Pringles o de silla de montar. Parece que la geometría de nuestro particular Universo es de tipo plana, con una k=0, en el que la suma de las densidades de los tres elementos que lo integran, radiación, materia y energía oscura, es igual a la crítica. Lo hemos podido comprobar gracias a distintas verificaciones basadas en la observación del Cosmos, entre otras, lo que nos dice la radiación de fondo de microondas.
Echemos ahora una ojeada más cuidadosa a los dos bloques que se restan en la ecuación de Friedman. Para el caso de materia no relativista, aunque el razonamiento sirva también para un Universo de radiación, el primer bloque, el de la densidad ρ, tiene que variar en el tiempo de acuerdo a a-3 -con el volumen-,[4] mientras que el segundo, el de la curvatura, vemos que lo hace según a-2. Densidad de energía vs. curvatura. Como con el tiempo la expansión va incrementando el factor de escala a(t), podemos inferir que a la par van disminuyendo los valores de ambos sumandos, aunque el ritmo de disminución provocado por el factor a-3 lógicamente va a ser mayor que el provocado por el factor a-2. Lo que quiere decir que, en el caso de un universo cerrado con k positivo, el sumando de densidad va a ir perdiendo posición frente al de curvatura.
En algún instante la constante de Hubble, inicialmente positiva, se hará cero, momento en el que la expansión va a pararse, pasando la gravedad a dominar la dinámica del Universo. Podemos pensar que, consolidada esa coyuntura, aun habiendo mucha energía antigravitatoria que “empuje” hacia un universo abierto, ha llegado de nuevo el momento de la materia cuando la velocidad de crecimiento de a(t) comienza a hacerse negativa y el factor de escala se va haciendo cada vez más pequeño: la curvatura le habrá torcido el brazo a la energía oscura y acabaremos con un universo contrayéndose sobre sí mismo, lo que conocemos como un universo cerrado.
Podemos hacer un razonamiento, aunque opuesto, pensando en una curvatura k negativa: en ese caso el crecimiento del factor de escala a(t) conduce siempre a una constante de Hubble positiva. Nos encontramos en el caso de un universo en continua expansión, un universo abierto. Finalmente, si la curvatura es cero, el crecimiento de la constante de Hubble, aunque siga siempre aumentando, se irá ralentizando con el tiempo al estar afectado de un factor a-3. Recordad que estamos analizando el caso de un universo con solo materia no relativista sin constante cosmológica.
En la siguiente tabla se recoge los diversos parámetros mencionados en la entrada para un universo plano:[5])
|
Tipo de población |
W |
ρ |
a(t) |
H |
|
Radiación |
1/3 |
α a-4 |
α t1/2 |
α 1/(2t) |
|
Materia |
0 |
α a-3 |
α t2/3 |
α 2/(3t) |
|
Energía oscura |
-1 |
Vacío verdadero del campo de la energía oscura |
α eHt |
Cte. |
En términos generales, el parámetro de Hubble, teniendo en cuenta la participación de todos los personajes, curvatura, materia, radiación y energía oscura, sigue la siguiente ecuación:
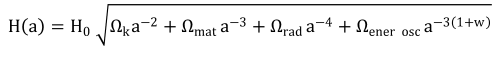
siendo los parámetros Ω las participaciones relativas de cada elemento en la densidad total de energía del Universo.[6] Si analizamos la ecuación podemos constatar de nuevo lo dicho un par de párrafos más arriba: a medida que el factor de escala aumenta, la incidencia de los sumandos va decayendo a excepción del de la energía oscura, que puede hacerse constante cuando w tome el valor -1 -caso típico para la energía oscura- y se hará cada vez más relevante cuando w sea más negativo que -1 -caso de la energía fantasma-.
Todo lo anterior son sólo datos para el análisis que no nos deben asustar ni debemos apartar de nosotros buscando panoramas más intuitivos y atractivos. Más allá de tantas k’s abstractas, tantas “planitudes” o “esfericidades”, y tantas arideces teóricas… siempre debe quedar revoloteando en nuestras mentes la imagen vivencial y diría que “épica” de nuestro Cosmos, el cómo la curvatura, la forma, está condicionando la acción de la materia/energía que contiene el universo; y la tensa relación entre la materia gravitatoria y la energía oscura, la una comprimiendo el espacio mientras la otra trabaja para expandirlo. La guerra de Troya.
Toda esa teoría aplicada a la evaluación de la evolución del Universo dibuja varios escenarios posibles (ver figura siguiente), que no tienen por qué ajustarse a lo que pase o pueda pasar, ya que el Universo puede dar muchas sorpresas a nuestros conocimientos. Vemos en esa figura que todas las casuísticas propuestas coinciden en la abscisa temporal denominada como “Hoy”. Es nuestra referencia ya que, suceda lo que suceda, hoy observamos el Universo tal como lo observamos. Anclados desde ese punto temporal fijo analizamos de qué manera pudo transcurrir su infancia o cómo va a discurrir su vejez. En el caso de materia muy abundante, Ωm=5, densidad muy alejada de la crítica, y sin energía oscura, el pasado dibuja una fuerte ralentización de la expansión dado que los procesos suceden con mucha rapidez. Eso hace que el punto de partida de la curva naranja, el inicio del Universo, esté situado cronológicamente más cerca de nosotros que en las otras alternativas: la edad actual del Universo sería menor que la que pensamos que tendría en un caso de geometría plana-euclidiana (curvas verde o roja). Cargados de exageración literaria podríamos decir que con cinco veces la masa necesaria aún se percibe el olor de la pólvora del Big Bang.

Casos teóricos de evolución del Universo. Los valores de Ω son los de hoy. La densidad de la radiación se considera despreciable ya que la contribución de los fotones es muy pequeña: Ωγ = (4.9 ± 0.5) × 10−5 (Imagen: NASA, WMAP, fair use)
El primer escenario que podemos analizar se corresponde con un Universo en donde la materia domina por goleada. Ya podemos intuir que nos vamos a encontrar con una tremenda acción gravitatoria que curvará el tejido del Universo hacia un mundo cerrado. Tras el impulso inicial de la inflación la expansión del Universo sigue su curso aunque cada vez más ralentizado por el tirón gravitatorio negativo que producía su materia. Como ya hemos comentado antes, en ese mundo el parámetro de Hubble se ralentiza hasta llegar a valer 0, momento tras el cual la expansión seguirá un claro sendero negativo hasta que el Universo vuelve a ser un punto compacto parejo a como fue el de su nacimiento. Lo podemos ver en la curva naranja de la figura siguiente, en la que se establece la condición de que la densidad de la materia sea cinco veces la crítica.
Sigamos jugando con la cantidad de materia en el Universo y sigamos argumentando de forma teórica: no hay energía oscura. Vemos que las curvas verde y azul, Ωm 1.0 y 0.3 respectivamente, ahora sí que no se frenan y parecen buscar un crecimiento moderado hacia el infinito. En el caso de la curva verde la densidad de la materia es exactamente igual que la densidad crítica (Ωm = 1.0) por lo que nos encontramos en el caso de un universo plano, aunque ya sabemos que no es nuestro mundo, en donde la energía oscura aporta más del doble de densidad que la materia. La curva azul corresponde a un mundo abierto, geometría hiperbólica, en el que la masa es tan poca que no puede vencer el empuje expansivo prolongándose hacia el futuro un crecimiento progresivamente ralentizado del Universo (pasa lo mismo con la curva verde). En la nota 6 hemos comentado que para el caso de que solamente haya materia no relativista la constante de Hubble crece en el tiempo según 2/(3t). Es decir, el ritmo de expansión se va frenando. La expansión se hace cada vez más “lenta”. Y mirando hacia atrás, el comienzo del Universo se adelanta más o menos en consonancia a si hay más o menos materia.
Vayamos ahora a lo que parece ser el mundo que observamos en donde hay energía oscura, además con la proporción 7 a 3 con la materia, tal como configura la curva roja. Entre ambos suman la densidad crítica, por lo que estamos otra vez en un caso de Universo plano. Pero muy distinto al de la curva verde… la energía oscura, con su densidad mantenida constante y continuamente embalsada a lo largo de los eones llega a ser infinitamente mayor que la de la materia. Tras ese momento la energía oscura, casi solitaria, produce una seria alteración en la dinámica con el resultado de un crecimiento exponencial a(t) α eHt (ver nota 5), siendo en ese caso H, la constante de Hubble, efectivamente constante.
Hasta aquí hemos contemplado diversos casos teóricos de evolución del Universo apoyándonos en los conceptos cosmológicos más básicos.[7]
En la próxima entrada continuaremos con ese tema particularizando en algunas de las teorías más conocidas y curiosas.
- El cosmos parece estar dominado por un agente de carácter desconocido cuyo efecto es equivalente al de una anti-gravedad y que existe a las mayores escalas. Este agente podría explicarse en términos de la constante cosmológica introducida por Einstein, aunque también podría admitir descripciones físicas de otro tipo, como energía oscura, quintaesencia, u otras. [↩]
- Recordemos de la entrada anterior: a(tx).[AB(t = 0)] = [AB(t = tx)] [↩]
- Eso que parece tan intuitivo, el que la materia/energía de cualquier tipo condicione la expansión, tiene su explicación. Supongamos un cohete que debe abandonar la Tierra sin volver a caer. Su energía cinética debe ser superior a la potencial gravitatoria. Pasemos esa misma idea a una teórica e inmensa esfera en el Universo. Llena de masa distribuida uniformemente y que escapar de la atracción gravitatoria interior y salir “volando”. Como ya sabemos que la masa/energía del exterior de la esfera se compensa y no ejerce influjo, según sea la diferencia entre la energía cinética y la potencial de la masa/energía de su interior se expandirá o volverá a “caer” colapsándose. Sobra decir que si la energía neta es cero se comportará como un universo plano y estable. Veámoslo con alguna fórmula: La masa M contenida en la esfera de radio r será M= ρ (4πr3/3) siendo ρ la densidad de materia/energía. Como hemos dicho la energía E por unidad de masa es la suma de su energía cinética (1/2)v2 debida a la velocidad de expansión, v=H/r -siendo H la constante de Hubble-, y de su energía potencial gravitatoria G.M/r -siendo G la constante gravitatoria de Newton-. Es decir, E = v2/2 – G.M/r. Si sustituimos aquí M y v encontramos fácilmente la siguiente relación: E = (1/2) v2 (1-Ω), siendo Ω = ρ/ρc, y ρc la densidad critica del Universo de la que hemos hablado ya muchas veces. Si Ω es mayor que uno la energía E es menor que cero y el universo colapsa. Por el contrario, si es menor que uno el universo se expande y si es igual a 1 permanece invariable en una perfecta planitud. [↩]
- Es lógico, ya que la densidad de la materia confinada en un volumen es inversamente proporcional al valor de ese volumen. Si se duplica el radio de una esfera, su volumen se multiplica por ocho. V0(a03) → Vt(at3), la densidad de la materia variará inversamente al cubo del factor de escala a(t). En un mundo dominado por la radiación, como al expandirse el Universo se alarga la longitud de onda de esa radiación según a(t), al efecto exponencial 3 por la variación volumétrica se le añade un factor a(t) a la variación de la densidad de la radiación, que seguirá por tanto una relación inversa con la potencia cuarta de a(t). Y si nos atenemos a la energía oscura, su densidad es constante con el tiempo al ser el resultado del potencial de un campo de tipo inflacionista de valor constante y continuo en el tiempo y el espacio. En la ecuación de Friedman Λ tiene unidades de una inversa de longitud al cuadrado, lo que indica que podría evolucionar con el tiempo según a(t)-2 al igual que la influencia en la curvatura. Aunque realmente varía, como podemos ver en la fórmula presentada más abajo en el texto para H, según a-3(1+w) siendo w la constante que define la función de estado del Universo, como vimos en la entrada anterior. [↩]
- Si nos centramos en el universo plano, k=0, la ecuación de Friedman se simplifica como (ả/a)2 = 1/3 (8π G ρ) y usando ahora las correlaciones “densidad/factor de escala” ya mencionadas en el texto, ρ α a-3(1+w), llegamos a las siguientes soluciones para la evolución del factor de escala a=f(t):
(i) Radiación (relativista) (w=1/3): con la densidad evolucionando como ρ α a-4 resulta que a(t) α t1/2, siendo la constante de Hubble H = 1/(2t). Así se comportó el Universo desde el final de la inflación hasta que tuvo unos 104 años.
(ii) Materia no relativista (podemos asemejarlo al polvo) (w=0): con la densidad evolucionando como ρ α a-3 resulta a(t) α t2/3.
En un universo dominado por radiación relativista (w=1/3), el factor de escala evoluciona como a(t)∝t1/2, mientras que en un universo dominado por materia no relativista (w=0), evoluciona como a(t)∝t2/3. Aunque 2/3>1/2, el universo bajo radiación crece más rápidamente porque la radiación tiene una mayor densidad inicial y ejerce presión (p=ρ/3), lo que acelera la expansión en tiempos tempranos. Por otro lado, la materia no relativista (p=0) no genera esa presión adicional, resultando en una expansión más pausada. Así, la clave está en que, aunque el crecimiento del factor de escala es más lento en términos relativos para radiación, el ritmo inicial de expansión inducido por la presión es mucho mayor, lo que explica por qué el universo crece más rápidamente en este caso. acelerando la expansión. La constante de Hubble sigue la evolución temporal H = 2/(3t). Así ha sido el Universo casi toda su existencia. En el mundo de la materia la temperatura evoluciona con el tiempo según T α t-4/3
(iii) Energía oscura (w=-1): con la densidad que permanece constante el resultado es un crecimiento exponencial a(t) α eHt, siendo en ese caso H, la constante de Hubble, efectivamente constante. De hecho, el Universo entrará en una fase de expansión acelerada siempre que 0 > 3P+ ρ, -1/3>w, donde ρ y P corresponden a la densidad de energía total y a la presión del contenido respectivamente.
Los anteriores párrafos proviene de lo dicho en estas dos publicaciones, esta y esta. [↩]
- En la historia reciente del Universo el valor medido del parámetro w que correlaciona presión y densidad de energía se mueve en el intervalo −1,2 < w < −0,9 a 3σ de grado de confianza. [↩]
- En este interesante artículo se da el resultado del estudio de las posibles historias de la expansión del Universo a la luz de los datos que acompañan a las supernovas Ia. En su figura 4 podemos ver unas curvas de las posibles historias más ajustadas que lo dibujado por la figura de más arriba. [↩]

The El destino del Universo 2: Dinámica de la expansión by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.





{ 4 } Comentarios
Interesantísimo, como siempre.
Saludos
El tiempo en la figura ¿no sería en miles de millones de años en lugar de billones?
Hola Gabriel,
efectivamente es lo que tu dices. Ya está corregido. Defectos de una traducción rápida desde los billones americanos. Gracias.
Un cordial saludo. Con respecto al ¨problema del valor de la constante cosmológica¨, quisiera colegiar con los interesados en el tema una posible solución basada en que: 1ro- Se puede demostrar IRREFUTABLEMENTE que la la unidad de medida que realmente le corresponde a la Constante de Planck es: ¨ Acción/ OSCILACION¨, es decir que, en realidad en este caso la unidad de medida ¨Acción¨ está CONDICIONADA! 2do- La inclusión de este término físico en la unidad de medida de la Constante de Planck permite aceptar que ¨el valor de la Incertidumbre en el nivel fundamental de un Oscilador Cuántico admite el CERO, y por lo tanto, el valor de la Energía de EXCITACION de una coordenada de Punto Cero puede ser NULA¨!
Escribe un comentario