más teoría

En la entrada anterior presentamos a un gran momento del Universo: la recombinación. El Universo parió a los primeros átomos y la radiación quedó libre de la materia, o viceversa, lo que permitió el inicio de los procesos de la definitiva compactación gravitatoria que ha dibujado las estructuras actuales del Cosmos. Nuestra serie sobre la Biografía del Universo continúa ahora con un objetivo: vamos a intentar destripar los misterios velados en la foto de la radiación de fondo de microondas. Lo que era ya quedó dicho en la última entrada. Para nuestro nuevo propósito contamos con el análisis de su espectro de anisotropías -su ligerísima falta de homogeneidad espacial-, que iremos deshojando al igual que podemos hacerlo con el de frecuencias de las emisiones de un cuerpo negro.

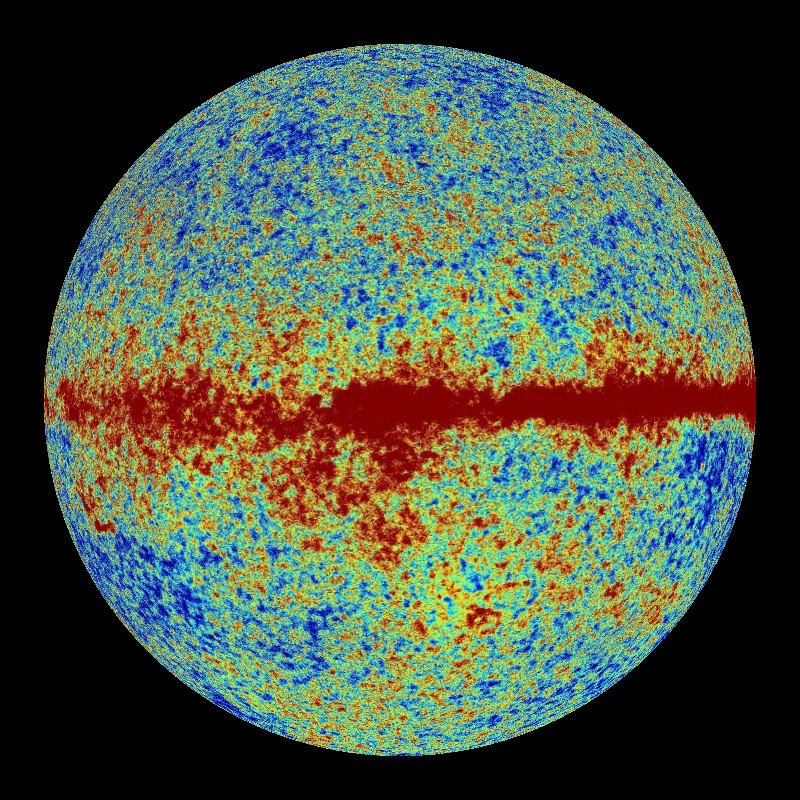
Esta imagen del fondo de microondas es una esfera convexa, como una luna, aunque la realidad nos dice que se trata de una bóveda celeste cóncava, como un planetario, desde la que nos llega tan lejana radiación. La franja horizontal roja es luz emitida por nuestra mucho más cercana galaxia. (Imagen: WMAP-NASA, dominio público)

Antes de seguir ya veis que me ha interesado introducir una modificación de la imagen que apareció en el capítulo anterior del fondo de microondas. Creo que es bueno pasar unas páginas atrás para mantener en la mente la original, aunque ahora la presento en su forma más auténtica, esférica y no plana. Representa la superficie esférica más lejana desde donde nos viene la radiación de fondo de microondas. Imaginémonos a nosotros como observadores situados en el centro de esa esfera desde donde contemplamos su grumosidad. Es como si se tratara del espectáculo de un planetario en el que vemos el aspecto del cielo con estrellas y planetas, pero en ese caso admirando la más vieja cara del Cosmos. Sabemos que en lo que vemos, a pesar de las inhomogeneidades aparentes, hay unas simetrías decisivas troqueladas por las anisotropías del Big Bang, las cuales llevan encriptada mucha información:

• la información de quiénes las hicieron como son, es decir, la composición de la materia -bariónica y oscura- y su relación con la radiación; y
• la información de lo que hicieron, el ritmo de expansión del Universo -constante de Hubble- y de su curvatura, que dependen de la cantidad de materia y energía total existente.

Sin duda imaginamos que la realidad de su estudio debe ser harto compleja, pero los cosmólogos lo han conseguido. Todo pasa por obtener la información, ordenarla, descomponerla en funciones simples para su estudio e integrar lo que nos dicen esas funciones.

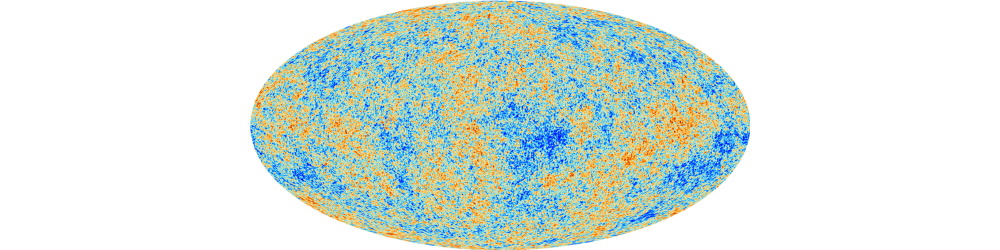
Esta imagen es el desarrollo en 2D de la superficie esférica más lejana,desde nos viene la radiación de fondo de microondas. Imaginémonos a nosotros como observadores situados en el centro de esa esfera desde donde lanzamos conos visuales que atrapan pequeñas áreas circulares de esta superficie. Es el comienzo de lo que se explica en el texto (Imagen: European Space Agency, ESA, non-commercial use)

La información nos la ha dado instrumentos tales como los del satélite COBE o el telescopio Planck situado a 1,5 millones de kilómetros de la Tierra. Hay que decir que si nos moviéramos hasta otro punto distante y lanzáramos allí un Planck, y limpiáramos las alteraciones ajenas a las frecuencias del fondo, obtendríamos una imagen prácticamente igual a la que conocemos. Así es de uniforme en todo el Universo.

Pero aun así nos parece muy dispersa y grumosa, por lo que la vamos a ordenar. Para ello nos asentamos en el sillón giratorio de nuestra casa y lanzamos hacia todas las direcciones unos conos visuales que abarquen pequeños círculo del lejano escenario. Círculos de distintos diámetros que nos permitan enfocar los “granos de granada” con sus horizontes acústicos, que es lo que realmente queremos detectar.

¿Cómo determinamos los armónicos en el fondo de microondas? Buscando su espectro de potencias. Lo vamos a hacer parcelando su imagen en áreas que nosotros los observadores vemos cubiertas por un ángulo θ, y que podemos imaginar como pequeños círculos. Los conos visuales de los que hablaba más arriba. Medimos en cada una de estas áreas la ΔT, la mayor diferencia de temperaturas entre los puntos de su interior. A continuación, determinamos para cada θ un valor promedio de ΔT, por ejemplo, para zonas de un ángulo de 1º la ΔT promedio es de 0,0075K, con lo que obtendremos una serie de [ΔT, θ] que luego se transcribe a una curva. Aunque realmente no se usa θ, sino otro parámetro equivalente: el momento multipolar l, que aproximadamente se correlaciona con el ángulo según θ~180º/l. Lo que realmente hemos hecho con esta discriminación angular es algo así como si al ir disminuyendo el ángulo de observación hubiéramos ido añadiendo filtros más finos que resaltan las anisotropías ocultas para los filtros anteriores de mayor ángulo, menos finos. Es como realizar un viaje desde las zonas más profundas y borrosas en la edad del Universo hacia las más actuales. El resultado de este trabajo es la curiosa curva siguiente.

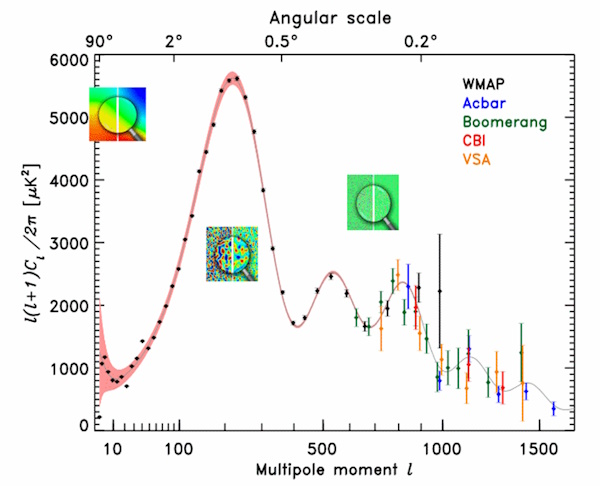
El espectro de potencia de las anisotropías de la temperatura del fondo de radiación de microondas en función de la escala angular, según datos aportados por diversos experimentos, datos que se superponen con bastante precisión sobre la línea continua de color rosa que corresponde a la curva teórica calculada (Wikimedia, dominio público)

Una curva con una serie de máximos que, aunque parezca sorprendente, nos va a dar una información fundamental del Universo, corroborando lo que ya sabíamos por otras experiencias y observaciones. El primer máximo es un pico relacionado con las zonas de máxima compresión de la materia bariónica, que ya sabemos que es igual a decir “de temperatura máxima”.^[1]  El segundo, de menor altura y en un momento multipolar mayor, indica que al mirar con otro zoom podemos observar cómo se ha añadido un efecto de rarefacción que atempera la temperatura. El tercero atempera la tendencia al enfriamiento, lo que indica que a escalas aún menores se ha añadido al segundo pico un nuevo impulso de compresión, por lo que indica un nuevo refuerzo a la temperatura. Suena tremendamente a lo que decíamos en las entradas anteriores acerca de los tres armónicos primeros de la onda de sonido. Y realmente es que estamos hablando de lo mismo.

Lo cual parece también decir que la curva de anisotropías lleva en sus patrones cierta información del horizonte acústico y su desarrollo. Lo que, como ya hemos comentado, nos conduce a la información sobre el tipo de materia y radiación existente en el Universo, sus densidades y la curvatura del mismo. Todo un regalo. Hay que recalcar que la curva dibujada utilizando datos experimentales se ajusta perfectamente a la curva teórica que se obtiene por “simple” cálculo, aplicando los criterios del Modelo Estándar y el concepto ya explicado en otras entradas de las ondas sonoras del plasma, lo cual nos hace sentir bastante seguros mientras manejamos nuestras hipótesis y teorías. Vamos a analizar con un poco más de detalle la información oculta en este espectro.

Explicación gráfica de lo que se “ve” según distintos momentos multipolares (Imagen: NASA, libre uso no comercial)

En la imagen anterior hay como tres zooms. El de la izquierda es el menos nítido y es así porque dispone de menos información. Solo han llegado los fotones más primerizos, próximos al horizonte de la recombinación: estamos observando al Universo en las grandes escalas. A medida que nos desplazamos hacia los otros dos zooms se va incorporando más y más información, por lo que cuanto más a la derecha estemos no solo estaremos contemplando los momentos lejanos en el tiempo sino también que estaremos incorporando progresivamente información de momentos cada vez más actuales. A la derecha estaremos viendo casi el mundo actual.

En la curva la línea roja horizontal es la teórica que correspondería al caso de que no hubiera ninguna anisotropía, es decir, en el caso de que nuestro universo fuera perfectamente homogéneo. La izquierda de la curva ondulante corresponde a lo que se observa bajo ángulos muy grandes, es decir, con poquísima definición en la imagen. Lo hemos identificado como los viejos viejos tiempos. Estamos viendo el Universo casi en su conjunto y sin resolución para observar sus detalles. A estas escalas, la circunstancia que domina el patrón de temperaturas en la imagen de microondas es la fuerza de la gravedad, que creemos generada en su mayoría por la materia oscura. Es la que domina la plaza pública. En estas escalas, pues, las zonas con temperatura por debajo de la media corresponden a aquellas en las que los fotones tenían que salir de las regiones con mayor acumulación de materia oscura, lo que les hizo perder un poco de energía en el proceso al intentar escapar del intenso pozo gravitatorio. Por el contrario, las zonas más calientes corresponderían a menores acumulaciones de materia.^[2] Cuando promediemos estos patrones correspondientes a grandes escalas buscando nuestro ΔT, obtendremos en cada una de ellas una imagen burda y casi a ojo de pájaro, mostrando unos valores equivalentes al promedio del conjunto, que es del orden de 10^-5K. Por ello no nos extraña el que en el rango de momentos multipolares pequeños la curva presente valores bajos para cada punto, próximos a los de la recta teórica y con una gran incertidumbre (zona gris).

Vayamos más hacia la derecha, en donde se empiezan a apreciar los detalles, los patrones que dejaron las ondas de sonido. Como podemos ver en la figura siguiente, que dibuja la posible distribución de materia causada por una onda de sonido fundamental en el momento de la recombinación, la densidad de la radiación -los fotones- no se concentra en donde hay una gran densidad de materia oscura, sino en el frente de ola de materia bariónica. Por esta razón los fotones más calientes se encontrarán en estas últimas zonas, las de compresión, y los más fríos en las zonas de materia oscura. Esta casuística es la que vamos a analizar.

Distribución de la materia y la energía de una fluctuación cuántica primordial en el momento de la recombinación (Imagen: a partir de Daniel J. Eisenstein, Physics today, abril 2008, fair use)

Fijémonos ahora en el primer pico de la anterior curva de anisotropías. Es el máximo de la curva, y se da en el entorno del momento multipolar de l=200, equivalente a zonas abarcadas por una amplitud angular de aproximadamente 1º. Como este pico es el mayor de los máximos ya sabemos que tiene que tener alguna relación con aquellas zonas en donde se dieron las diferencias de temperatura más extremas. Lo que fue motivado por una compresión gravitacional provocada por la materia oscura y la bariónica. Lo que nos permite presuponer que su altura algo tendrá que ver con la cantidad de esas materias en el conjunto del Universo.

Pero centrémonos en el análisis de lo que estamos viendo desde nuestro puesto de observadores en la Tierra, los fotones de la recombinación que provienen de puntos entre los que se dio un mayor contraste térmico y cuya separación física está cubierta por un ángulo de 1º. Sabemos por la teoría que hemos explicado en el capítulo 16 que este intervalo particular es la consecuencia de la “congelación” del armónico fundamental de la onda de sonido en el ámbito espacial de nuestro ya famoso “grano de granada”, cuando el Universo tenía 380.000 años. El ángulo de 1º abarca una semilongitud de onda del armónico principal lo que corresponde a la longitud del horizonte acústico en el momento de la recombinación. Los cálculos más precisos disponibles nos dicen que mide unos 490 millones de años luz a día de hoy, después de haber crecido 1.100 veces.

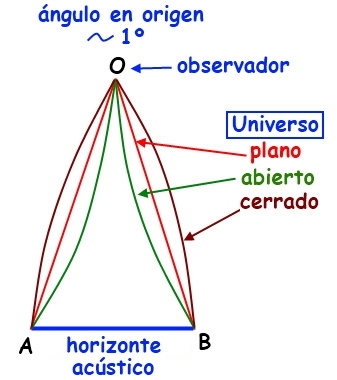
El que sea 1º tiene mucha miga ¿por qué? porque nos sirve, entre otras muchas cosas, de vara de medida para investigar sobre la curvatura del Universo que a su vez depende de la materia/energía que contiene. En la figura anterior intentamos visualizar lo que sucede según el tipo de curvatura del Universo, que puede adoptar tres tipologías: la plana, la positiva -cerrado- y la negativa -abierto-. Todo depende de la cantidad de materia y energía que se encuentra en el Universo. Teóricamente se ha definido una densidad de materia/energía que llamamos “crítica”, que corresponde a la que hace que las ecuaciones que rigen la dinámica del universo -las de la relatividad que correlacionan forma y energía- nos den para éste una geometría -la métrica que lo rige-^[3] plana. En un universo plano los fotones que hubieran salido desde los extremos del horizonte acústico describirían una trayectoria lineal hasta llegar a nosotros los observadores, trayectorias que formarían un ángulo que vamos a llamar α. Si el universo fuera abierto, el ángulo de arribada sería menor que α y si fuera cerrado sería mayor.^[4]

Pues bien: veamos qué es lo que observamos. Tenemos tres lados de un triángulo conocidos y medidos: la base es el radio de nuestro grano de granada, el doble del horizonte acústico, y los otros dos lados la distancia al borde del Universo observable. También hemos medido el ángulo α y es igual a 1º. A partir de esos datos, los cosmólogos han podido medir con gran precisión la suma de los tres ángulos, y es justamente 180º. Curioso, ¿verdad?^[5]

Se trata, por tanto, de una geometría puramente euclidiana, lo que nos dice claramente que nos encontramos con un Universo que la cumple, luego geométricamente se comporta como si fuera plano. Tanta maravilla esconde un pequeño “pero” que no invalida la conclusión, porque la verdad es que no conocemos con precisión absoluta los parámetros que conforman este triángulo. Con ello quiero decir la velocidad del sonido en el plasma inicial -que condiciona la longitud del horizonte acústico- y la constante de expansión del universo -que condiciona los otros dos lados del triángulo-. De todas formas, los expertos nos aseguran que la confianza con que lo decimos es del 95%. Yo apostaría mi sombrero en favor del Universo plano.

Con lo dicho no nos sorprende el que los estudios teóricos que se han hecho para definir mediante cálculo el espectro de frecuencias de la radiación de fondo de microondas determinen que, para el caso de una distribución de materia/energía propia de un universo plano, se debería de dar un pico en campos angulares de aproximadamente 1º, un momento multipolar de 200. Si disminuye la densidad de materia/energía el universo se tiene que abrir, hacerse hiperbólico.^[6] Y así se observa en los estudios teóricos realizados cuyos resultados podemos seguir en la serie de imágenes de más abajo y que fueron realizados a partir de nuestros modelos cosmológicos. En ellos se ha hecho variar la cantidad de materia y realmente se ha observado como este primer pico se movía hacia multipolos mayores -definición angular menor-, lo cual es lo lógico porque en este caso los fotones, como habíamos comentado en el párrafo anterior, cierran los ángulos de sus trayectorias. Lo explicamos.

Evolución del primer pico dependiendo de la cantidad de materia que se considere en el Universo (lo que define su geometría). (Imagen: Wayne Hu, Universidad de Chicago, fair use)

Hay dos curvas teóricas: la azul, que tiene en cuenta, además de  la materia, a una energía intrínseca -puede ser pensada como la energía oscura, aunque ahora estamos en un nivel de cálculo teórico- y la amarilla, que sólo tiene en cuenta a la materia. La barra rosa de la derecha indica el parámetro equivalente a “densidad crítica menos densidad de materia” (de lo que sea la densidad crítica hablaremos unos párrafos más abajo).^[7] A mayor barra rosa, menor es la participación de la materia -bariónica y oscura- en la densidad crítica, y por tanto más nos alejamos de un universo plano hacia uno abierto.

Si nos fijamos en la curva amarilla vemos que al disminuir la materia -cuando sube la barra rosa- el primer pico (en general todos los picos) se desplazan desde una posición l=200 hacia multipolos mayores, que es lo que podíamos esperar. Vemos que en el proceso de la barra rosa descendiendo -es decir, el universo está en camino hacia la geometría plana- el primer pico se aproxima y llega a un multipolo 200, lo que equivale a una definición angular de 1º. También vemos que en la curva azul, en la que se tiene en cuenta la energía oscura, el desplazamiento es casi inexistente, lo cual nos indica que debe haber mucha cantidad de esta energía intrínseca, ya que su influencia anula prácticamente cualquier variación de la materia.^[8] Pues bien: justo todo eso que nos ha dicho el análisis teórico es lo que hemos visto luego en la realidad al estudiar los datos obtenidos por nuestros instrumentos.

Pero insistamos sobre eso de que el Universo sigue una métrica plana. Evidentemente, un universo plano no tiene sólo dos dimensiones espaciales. Al menos nuestra experiencia nos dice que podemos apuntarle tres direcciones ortogonales: arriba-abajo, derecha-izquierda y delante-detrás, lo que no nos impide imaginar desde dentro la idea abstracta de planitud. Un ser que nos contemplara desde la dimensión n+1, siendo n el número de dimensiones de nuestro Universo, sería capaz de explicarnos con soltura la evidencia para él de que nuestro Universo es “plano”. Pero ¿por qué es tan importante que sea plano?

Tiene que ver con la cantidad de materia-energía que contiene. Si hubiera mucha habría también mucha gravedad y el universo colapsaría en forma de una esfera cerrada cada vez más curvada y pequeña. Si hubiera poca, la expansión seguiría acelerada hasta “rasgar” su tejido, cada vez más abierto y con más curvatura negativa. Cualquier desviación positiva o negativa con respecto a un punto de equilibrio, aunque hubiera sido mínima, con la expansión del universo se hubiera realimentado exponencialmente para caer en el mundo “colapsado” o en el mundo “rasgado”. Pero vemos que el universo no parece comportarse ni de una ni de otra manera, lo que quiere decir que tiene que tener una densidad adecuada para que suceda lo que observamos, que no habrá variado mucho desde el inicio. Y ello implica que su densidad de materia y energía, al ser plano, deba coincidir con la crítica: 0,9×10^-29 gr/cm³.

Normalmente se habla no de valores absolutos, sino del porcentaje de participación de la densidad de cada uno de los componentes en la densidad crítica total. Estas participaciones se designan con la letra Ω y por tanto, si en el Universo coexisten tres tipos de materia o energía -la materia también es energía- como así creemos que es, se deberá cumplir:

(normalizado a la propia densidad crítica)        Ω₁ + Ω₂ + Ω₃ = 1      = (0,9×10^-29/0,9×10^-29)

En esa ecuación Ω₁ es la densidad de la materia bariónica, Ω₂ la de la materia oscura y Ω₃ la de la energía oscura. La posición del primer pico del espectro de la radiación de fondo nos asegura que la igualdad de arriba es verdad, que hay una densidad absoluta de 0,9×10^-29 gr/cm³en el Universo. ^[9]

Llegados aquí, con las neuronas calientes de tanta materia y radiación, nos va a convenir mirar solamente a los posos que se hayan podido decantar, si es que hay alguno. Voy a intentar resumir de todo el alegato anterior lo que básicamente nos dice el primer pico del espectro de potencia de las anisotropías de la temperatura del fondo de microondas: [1] Nuestro universo es plano, [2] con una determinada relación entre materia oscura y el tándem bariónica/radiación, que [3] hay bastante materia oscura… aunque [4] también hay otro tipo de participante. Dicho esto, en la próxima entrada continuaremos con el análisis de los armónicos encontrados en las anisotropías. Así que… nos vemos en el segundo pico.

1. Podéis repasar este aserto y todo el trasfondo de lo que viene en algunas entradas anteriores. En concreto ésta, ésta otra y también ésta última. [↩]
2. Esta correlación inversa entre la energía de los fotones y la densidad de materia gravitatoria es debido a lo que se conoce como corrimiento al rojo gravitacional. Los fotones no tienen masa en reposo, pero si energía (momento) que se ve afectada por la gravedad. A medida que van alejándose del pozo gravitatorio van perdiendo energía en su lucha contra la fuerza gravitatoria. A menor energía, menor frecuencia de onda y por tanto un corrimiento hacia posiciones de frecuencias rojas. La siguiente fórmula nos correlaciona como varía la frecuencia de un fotón emitido a un radio r₀ cerca de una masa gravitacional M y cuya frecuencia se mide a una gran distancia de dicha masa,

   

   a mayor masa mayor pérdida de frecuencia (menor energía, más frío, menor temperatura)  [↩]

3. La métrica es lo que nos permite calcular distancias en un espacio, y es el punto clave sobre su geometría, la que nos dirá cómo son en este espacio las distancias, los volúmenes o los ángulos. Para la relatividad especial tenemos que la métrica, que representaremos por ds², toma la siguiente forma ds²=-c²dt²+dx²+dy²+dz², que se transforma en la euclidiana si el universo es plano. Recordemos que en una geometría euclídea la suma de los ángulos de un triángulo es de 180º. Sin embargo, en un universo cerrado la suma de los tres ángulos es mayor que 180º, y en uno abierto, menor. [↩]
4. Es intuitivo. Si queremos coger algo que se encuentra en la cúspide de una esfera pegada a nosotros -geometría cerrada- debemos abrazarla abriendo los brazos -apertura de ángulo-. Si estamos junto a un caballo y su silla de montar -geometría abierta-, y queremos alcanzar algo en la parte más alta de la silla al acoplarnos a ella notaremos que los brazos se nos desvían hacia el interior de la curvatura de la silla de montar -cierre del ángulo-. Alcanzar algo situado sobre una mesa -geometría plana- solo nos exige el estirar los brazos con normalidad -ángulo normal-. [↩]
5. Podemos hacer un cálculo a palmos, como se suele decir. Estamos viendo una circunferencia -realmente un pixel de una esfera- de 1º sobre una “pantalla” que se encuentra a 46.500 millones de años luz, el borde del Universo alcanzable: 13.800 millones de años luz más los que añadió la expansión. Eso da aproximadamente un arco de 810 millones de años luz. Pero eso es lo que vemos ahora, es decir, debería ser algo parecido al horizonte acústico recrecido unas 1.100 veces para que la geometría fuera euclidiana y el Universo plano. El horizonte acústico recrecido a día de hoy mide 490 millones de años luz. No son los 810 millones de años luz prometidos, pero se asemejan. Como dije al principio, un cálculo a palmos en el que no hemos tenido en cuenta algunas auténticas incertidumbres como las mencionadas en el texto ¿y si la velocidad del sonido en el plasma no fuera de una valoración tan evidente? ¿y si la constante de Hubble hubiera variado en los 13.800 años de vida del Universo? A pesar de todo huele como que las anisotropías a 1º deben tener algo que ver con los volúmenes donde se daban las mayores diferencias de temperatura en la recombinación. Realmente son la misma cosa según los entendidos.. [↩]
6. El ángulo α es menor, lo que quiere decir multipolos mayores. [↩]
7. Realmente las densidades se han normalizado al valor de densidad crítica igual a uno. 1= incidencia de los bariones + incidencia de la materia oscura + incidencia de la energía oscura. [↩]
8. La gravedad tira menos y le puede la energía interna que expansiona el tejido espacio/tiempo. [↩]
9. A partir de los datos obtenidos por la sonda WMAP dedicada a la observación de las anisotropías en el fondo de microondas, así como de los del telescopio espacial Planck, conocemos las densidades para los tres constituyentes de toda la materia-energía en el universo: materia (bariónica y oscura); radiación relativistas (fotones y neutrinos) y energía oscura o constante cosmológica Λ. Y sus valores, relativos a la densidad crítica [↩]

The Biografía del Universo 18: Lo que nos enseña la radiación de fondo I by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.