Seguimos con la serie de modelos atómicos. En el anterior artículo terminamos con el modelo de Thomson, un par de artículos algo complicados, es verdad, pero tengo la esperanza de que el lector haya aprendido algo sobre dicho modelo. Los siguientes artículos volverán a ser conceptos previos de física general (es decir, sin enfocarlos a la física atómica) para aprender algunos conceptos necesarios al presentar el modelo atómico de Rutherford. El primero, es decir, éste, es en realidad una ampliación del artículo donde hablamos sobre la energía potencial. Y en él vamos a centrarnos en la energía potencial electrostática.
Recordemos una definición que di en su momento sobre la energía potencial:
Primero definí lo que es una fuerza conservativa. Recordemos; una fuerza es conservativa si podemos llevar un objeto desde un punto A a un punto B realizando el mismo trabajo lo llevemos por donde lo llevemos. Teníamos esta imagen:
Es decir, el trabajo realizado por una fuerza conservativa para llevar un objeto desde el punto 1 al punto 2 es el mismo tanto por el camino S1 como por el camino S2. Bien, una vez identificamos que una fuerza es conservativa podemos definir una energía potencial “asociada” a esa fuerza; de hecho no podemos definir la energía potencial como tal, sino su variación. La energía potencial es la energía que tiene un cuerpo por el simple hecho de estar sometido a una fuerza conservativa. Como en general las fuerzas suelen afectar a los objetos en cualquier punto del espacio, podemos decir por lo tanto que un objeto, solamente por estar en un punto del espacio tiene una energía potencial.
Vamos a profundizar algo más en esta idea. Nuestra situación es la siguiente: tenemos una partícula que sufre una fuerza, y es importante darse cuenta de que no nos importa qué ni cómo se crea esta fuerza, puede ser otra partícula (como la fuerza electrostática que veremos después) o puede ser un dios griego jugando a las canicas con nuestra partícula. La cuestión es, en fin, que nuestra partícula va a estar sometida a una fuerza; la clave está en que esta fuerza puede depender del punto en donde esté la partícula, pero en cada punto habrá definida una fuerza concreta que nosotros conocemos.[1] Por ese motivo, una vez conocemos la fuerza que actúa en todos los puntos, y como la energía potencial la definimos como la energía que tiene una partícula por estar sometida a una fuerza, podemos decir que si sabemos en qué punto está la partícula podremos saber qué fuerza actuará sobre ella y, por lo tanto, su energía potencial. Resultado: si conocemos la posición de una partícula conocemos su energía potencial y podemos pensar como que esa energía es debida a que la partícula está en esa posición concreta. Es importante también ser conscientes de que si la fuerza cambia por alguna razón ya no tiene sentido esto, ya que la energía que le correspondía a un punto P antes no será la misma que después. También es importante saber que, en muchos casos, la fuerza depende de la partícula que consideremos, así que, de nuevo, sólo nos sirve para un sola partícula, si queremos saber la energía que tendría otra partícula no podemos usar los valores que hemos calculado antes.
En resumen, podemos considerar que la energía es debida a la posición siempre que no cambiemos la fuerza ni la partícula. Por lo tanto, una partícula situada en el punto 1 de la imagen tendrá una cierta energía potencial, mientras que la partícula situada en el punto 2 tendrá otra energía potencial diferente.[2] ¿Qué relación hay entre el valor de la energía en 1 y en 2? Pues la variación de energía entre estos dos puntos (esto es, la energía en el punto 2 menos la energía en el punto 1) es precisamente el trabajo necesario para ir del punto 1 al punto 2… multiplicado por -1.
Lo que he dicho en este párrafo es lo mismo que dije en el artículo correspondiente hace ya más de un año,[3] sólo que lo he extendido un poco; por algo este artículo es una ampliación de aquel.
Bien, ahora centrémonos en una fuerza concreta, la fuerza electrostática, la que se rige por la ley de Coulomb, que, aunque no lo voy a justificar, resulta que es una fuerza conservativa.[4] Por lo tanto, debe existir una energía potencial electrostática, pero hay cierta característica de la energía potencial que aún no he resuelto. He explicado que cada punto del espacio tiene asociada un valor de la energía potencial y he explicado cómo se puede calcular la diferencia entre dos puntos, pero esto sigue sin resolver la cuestión inicial: ¿Cuánto vale la energía potencial en cada punto y cómo la calculamos? Porque si yo calculo que la diferencia de energía potencial entre los puntos 1 y 2 es de 100J, esto no nos dice si las energías absolutas son 0 y 100J o si son 500 y 600J, etc.
Pues afortunadamente no nos importa para nada el valor exacto. Lo único que podemos medir en un laboratorio son las variaciones de esta energía, y una partícula se comportará exactamente igual tenga 100J que 200J que 106J. Recordemos que, aunque intentemos describir el universo con números y ecuaciones matemáticas, estos números solo significan algo en nuestras cabezas. Así que los físicos suelen hacer un truco, a saber: busquemos un punto arbitrario del espacio que nos guste lo suficiente, y a ese punto le daremos de forma totalmente arbitraria un valor de 0J. A partir de aquí solo tenemos que calcular el trabajo realizado por la fuerza para llevar una partícula desde este punto a cualquier otro y tendremos el valor exacto de la energía potencial. Cómo elegir este punto es otra cuestión, quiero dejar claro que es una elección arbitraria, pero resulta que suele haber un punto concreto (o un conjunto de ellos) para los que el hecho de establecerlos como origen simplifica mucho las matemáticas resultantes. Para el caso de la energía electrostática se suele establecer el origen de potencial en un punto situado al infinito.
Energía potencial (con ecuaciones)
Ya vimos en el primer artículo de la serie (y lo acabamos de repetir en la primera parte del artículo) que la variación de la energía potencial es menos el trabajo hecho para ir de un punto a otro, por lo que si llevamos un objeto desde un punto A a un punto B, tenemos:
La última igualdad sale de la definición formal de trabajo mecánico, que para fuerza constante se corresponde con la conocida ecuación W=F·Δx. Para el caso de la fuerza electrostática entre dos cargas q1 y q2 tendremos
Aquí hay un par de cosas que debo aclarar. Primero de todo, lo que teníamos antes era el producto escalar de la fuerza por un diferencial de longitud, (que simplemente puedes considerar como una longitud muy pequeña),[5] pero en el producto escalar sólo afectan las componentes que tienen la misma dirección, por lo que, como la fuerza tiene dirección radial (r) el diferencial de longitud se convierte en dr; si no recordáis, hablamos de esto en el artículo sobre la ley de Gauss. Aún así os dejo un pequeño dibujo que puede ayudar a visualizar lo dicho.
La segunda cosa que quiero aclarar es el valor de la integral de 1/r2. No es mi intención enseñaros a integrar en este artículo, así que podéis buscar el valor en muchas tablas (o en Internet mismo, por ejemplo aquí) y veréis que efectivamente es -1/r, que es justo lo que he hecho yo al solucionarla.
Hay una tercera cosa que quiero dejar clara. Recordemos que en la fuerza de Coulomb lo que aparece en el denominador (así como el vector que define la dirección de la fuerza) es la distancia entre la partícula que crea la fuerza y la partícula que la sufre. En este artículo no he escrito r1,2 sino que lo he abreviado a r. Pero lo importante es que los rA y rB que aparecen al final son las distancias de los puntos A y B a la partícula que esta creando la fuerza.
Finalmente, quiero recordar y poner cierto énfasis en que estamos calculando la diferencia entre la energía potencial que tendría una partícula en el punto A y la energía que tendría la misma partícula en el punto B. Si releéis la parte sin ecuaciones veréis que el concepto de energía potencial es algo propio de la partícula y solamente depende de la fuerza que sufra y no de cuál sea la causa de esta fuerza.
Ahora la pregunta es, si elegimos el punto A como el origen de potencial (UA=0), ¿cuál es el valor de rA que simplifica al máximo la ecuación? Pues para un valor de rA infinito obtendremos:[6]
Ya para terminar el artículo voy a tratar un caso más particular. Si tenemos una partícula con carga 2e y otra con carga Ze, donde e es la carga de un protón con una distancia d entre ellas, ¿cuál es la energía potencial que tiene una de las dos partículas? Si elegimos el origen de potencial al infinito (como haremos de ahora en adelante siempre, a no ser que se especifique lo contrario), podemos usar simplemente la ecuación anterior, esto es
Recordad esta expresión, porque la usaremos más adelante en la serie (éste es en realidad el motivo por el que escribo este artículo).
Antes de terminar dejadme dedicar un último párrafo a la expresión que he puesto y a aclarar algunas cosas. La energía potencial que hay ¿es la energía que tiene la partícula de carga 2e, es la que tiene la partícula de carga Ze o es la energía que tiene una respeto a la otra? Quiero remarcar que la tercera opción NO ES CORRECTA: cuando he definido energía potencial siempre he hablado de una única partícula. Entonces ¿es la energía de la primera partícula o la segunda? Pues la respuesta es que las dos son correctas. Si consideramos que la partícula de carga Ze crea la fuerza y la partícula de carga 2e sufre la fuerza, entonces estamos calculando la energía de la partícula con carga 2e, si al contrario la partícula de carga 2e crea la fuerza y es la partícula de carga Ze la que sufre la fuerza, entonces estamos calculando la energía potencial de la partícula con carga Ze. Debido a que la fuerza que crean una y otra partícula son la misma, y la distancia, evidentemente, también. La energía potencial es exactamente la misma.
Creo que este artículo lo podemos ir dejando por aquí. En el próximo seguiremos con conceptos previos haciendo una segunda ampliación al artículo de conservación de la energía y el momento lineal, pues hablaremos de la tercera magnitud que nos falta. En general suelen haber tres magnitudes importantes que se conservan bajo ciertas condiciones; hemos visto ya la energía y el momento lineal, nos falta hablar sobre el momento angular. Hasta el próximo artículo.
- Esto se llama un campo vectorial y hablamos de él de forma muy fugaz en este artículo al hablar de campo eléctrico. [↩]
- Nada impide que la energías puedan ser iguales, pero, en general, serán distintas. [↩]
- Pido perdón por la tardanza de la segunda parte de la serie. [↩]
- Para los que sabéis algo del tema, tiene que ver con que su rotacional es cero. [↩]
- Recordemos que hablé de la integral en este artículo y simplemente es una suma de términos muy muy pequeños. [↩]
- Esto es, la diferencia ente la energía potencial cuando la partícula está en B y la energía cuando la partícula esté infinitamente lejos de “la fuente de la fuerza” [↩]

The [De Thomson a Bohr, historia de un átomo] 0-Conceptos previos 7: Energía potencial by Roger Balsach, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.







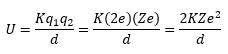


Escribe un comentario