Quiero agradecer a Macluskey su colaboración para escribir este artículo. No me fue sencillo exponer de manera simple y clara a la vez un tema en el que los músicos y los científicos suelen no estar de acuerdo, pues el lenguaje que hablan unos no siempre coincide con el que los otros hablan…y cada cual se queda un poco a medio camino. Así que yo he aprendido algo con él para preparar este artículo, y él algo conmigo, y ambos tenemos la esperanza de ser buenos “traductores” para todos en esta entrada de hoy.

Será éste un artículo excepcionalmente largo y denso en comparación con el resto de la serie (unas 11.000 palabras), pero esperamos que también fructífero.

Allá por el siglo VI a.C. adquiría un notable desarrollo la cultura de la Hélade, una nación que luego el Imperio Romano llamaría Grecia. En aquellos tiempos de la Hélade vivieron grandes sabios, de quienes heredamos gran parte de la ciencia moderna. Inventaron el triángulo rectángulo, los quebrados, Pitágoras y Thales nos legaron sus teoremas… Y también dirigieron su atención a la música. Descubrieron las propiedades físicas del sonido y pensaron en cómo se podían aprovechar para hacer arte. El enfoque matemático que hicieron de la música hace 2.500 años fue el antecesor directo de toda la teoría musical de Occidente en sus aspectos más fundamentales.

Sin embargo, en varios sentidos sus ideas no eran iguales que las nuestras. Por ejemplo, en el artículo anterior decíamos que en la antigüedad no existía un referente universal de afinación, es decir, un “diapasón”. ¿Cómo hacían entonces para saber la entonación exacta al empezar una música? Para comprender a fondo los razonamientos de aquella época debemos desprendernos por un momento del hábito de identificar inequívocamente con notas los sonidos de la escala.

Pongamos por caso el sonido que llamamos “DO”. Para nosotros es una nota con un significado específico. Pero para Pitágoras y Aristógenes, que estaban dedicados al asunto y también eran matemáticos, existía únicamente el concepto de sonido fundamental. Y sólo eso.

La frecuencia (ciclos por segundo) podía ser, en realidad, cualquiera. Luego, una vez determinada dicha frecuencia por las dimensiones de la cuerda, ésa era la base de cálculo de donde resultaba la escala, como una ordenación repetible a partir de cualquier otro sonido fundamental que posteriormente se eligiese. Recién, a partir de ahí, se puede dar un nombre propio a cada sonido. Es un acto muy similar al de dar nombres a los objetos, a las personas, y hasta a las ideas: exige precisión, pues todo ello es parte del lenguaje que usamos para comunicarnos. La nomenclatura, como expresión simbólica de lo que percibimos, o hacemos y pensamos, incluye a la música, pero no confundamos un hecho cualquiera con la forma de expresarlo, incluso por escrito.

¿Qué importancia tiene esta distinción en el tema que estamos estudiando?

Lo que terminamos de distinguir parecería tan obvio que ni merecería una mayor atención. Pero… veamos un ejemplo. Si dijésemos que un sonido fundamental es de 440 Hz, significa que la escala empezará por ese sonido. También decimos que ese sonido es la “nota LA”, que actualmente es el patrón universal de afinación, dado por el diapasón que suena con esa frecuencia exacta. Pero, cuando todavía no existían esos referentes ni los nombres actuales de las notas, era posible lo siguiente:

 

 

Para los músicos actuales esto tal vez les pueda resultar extraño, pero comprendamos que lo esencial es la disposición de los intervalos entre los sonidos de la escala, así como que esto se cumpla a partir de cualquier frecuencia elegida para el sonido fundamental. Y, precisamente, este último concepto era el que se manejaba en la antigüedad: la escala se “transportaba” entera a la altura (frecuencia) más conveniente para las voces o los instrumentos a ser utilizados. Si 440 Hz – diríamos hoy – no era bueno como sonido inicial para afinar la escala, pues se adoptaba cualquier otra frecuencia más cómoda y… empezaba la música.

Ahora sí, entremos de lleno en el tema que motiva el artículo más largo de toda esta serie, dada la gran complejidad del desarrollo de una teoría que habría de definir nada menos que toda la historia de la música occidental. No perdamos de vista, eso sí, la distinción que terminamos de hacer para poder comprender a fondo cuáles fueron los razonamientos que originaron algo tan fundamental para la música como son las escalas y los acordes.

 

Ese lío de las tonalidades…

¿Qué debemos entender exactamente por “tonalidad”?

El descubrimiento de las tonalidades no proviene de los griegos, sino que partiría de estudios muy posteriores, a medida que los músicos fueron abandonando el uso que los griegos hacían de las escalas. Surgiría entonces un nuevo concepto, que se impondría a partir del siglo XVI, donde el sonido fundamental de la serie armónica adquiriría un papel preponderante dentro de la escala. A ese sonido se le llamaría “tónica”, diciendo que da la “tonalidad” en que la música está compuesta. Además, se observaría que el 5° armónico, al ser también parte de la misma escala, era atraído hacia la tónica, que así funcionaba como si se llegase a un “punto final” en el discurso musical. A ese sonido que correspondía a la quinta nota de la escala, se le llamaría “dominante” a causa de esa característica peculiar. En la figura que vimos arriba, DO es la tónica y SOL es la dominante.

Escuchemos atentamente ese efecto de “punto final” cuando, en una melodía cualquiera, la última nota (tónica) es precedida de la dominante:

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

A partir de ese descubrimiento, y durante varios siglos, todos los giros melódicos y armónicos se desenvolverían alrededor de esa atracción de la dominante hacia la tónica. A ese sistema se le identifica como “tonalidad“.

Casi no cabe duda de que el descubrimiento de la tonalidad se debió a que las leyes del sonido ya habían sido estudiadas en el pasado por Pitágoras y Aristógenes, además de que ellos le dieron un sentido musical a las investigaciones. Remontémonos entonces al origen, pues es una historia llena de ingenio.

Con sus rudimentarios instrumentos se dieron cuenta de algo: si dividían una cuerda por la mitad y la hacían vibrar, se escuchaba un sonido similar, pero más agudo. Y si repetían una y otra vez la misma operación, dividiendo en mitades cada vez más pequeñas, obtenían cada vez lo mismo: el mismo sonido, pero más agudo cada vez.

La siguiente observación fue que la longitud de la cuerda es inversamente proporcional al número de veces que vibra, y que cuantas más veces vibre durante una unidad de tiempo, más agudo será el sonido que genere. Así que apuntaron cuidadosamente que al multiplicar por 2 las vibraciones obtenían un sonido igual al oído, pero más agudo, por lo que ambas cuerdas estarían en relación 2 a 1, o lo que es lo mismo, 2/1. Esto podría servir para componer música, debieron pensar… pero vaya, ¿qué música era esa, con un solo sonido, más agudo o más grave…? Sería el colmo de la monotonía.

Así que prosiguieron experimentando.

Como buenos filósofos griegos indagadores, se preguntaron qué pasaría dividiendo la cuerda por más números, como tres, cuatro…? Incluso, ¿qué pasaría dividiendo por números racionales, como el 3/2, el 4/3, etc, que para algo los habían inventado? No tardaron en descubrir que con una cuerda de una longitud 2/3 de la original se obtenía un sonido que no era igual que el original, pero que combinaba muy bien con el de la longitud original, que “pegaba”. Habían descubierto lo que hoy llamamos intervalo de “quinta” (3/2). ¿Por qué a ese intervalo de 3/2, o sea, de una vez y media la frecuencia original, se le llama “quinta”, y no de cualquier otro modo? Paciencia, ya lo explicaré unos párrafos más adelante.

Ese descubrimiento sería nada menos que el punto de partida de un sistema de escalas completo. Y también es el hueso más duro de roer para todos cuantos se aventuraron a estudiar alguna vez el asunto en libros de música, enciclopedias y demás, intentando aprender acerca de por qué las notas y las tonalidades son como son, y tratar de entenderlo… sin casi nunca terminar de conseguirlo del todo. Pero esto se justifica. Es que luego de tanto tiempo transcurrido, y ante la poca documentación arqueológica de que se dispone, lo único que los historiadores, musicólogos y matemáticos pueden hacer es tan sólo una reconstrucción de lo que muy probablemente fueron los razonamientos de aquella época tan lejana. Alrededor de todo ello siempre hay un margen de incertidumbre que no debemos olvidar. Quizás el razonamiento matemático sea el único capaz de dar fiabilidad a cualquier hipótesis de cómo se habría llegado hasta el concepto de la escala griega, y de ahí en más.

Por lo que se sabe, parece evidente que comenzaron a probar diferentes combinaciones que produjesen sonidos entre “1” y “2” (2/1), es decir, entre el de la cuerda original y el de la cuerda de mitad de su tamaño y doble frecuencia, como el 4/3 (frecuencia 1,3333… veces más alta), el 5/3 (frecuencia 1,6666… veces más alta), el 5/4 (frecuencia 1,25 veces más alta), etc., poniéndole mucha atención – y ya veremos por qué – al 3/2 (frecuencia 1,5 veces más alta). Muy posiblemente vieron que algunas de estas notas sonaban bien al oído cuando se las combinaba, mientras que otras no. Es muy plausible, por tanto, que simplemente desechasen lo que no les gustaba y se quedasen con lo que sí. Al fin y al cabo, lo hacemos todos, ¿no?

Al respecto, recordemos de paso que Pitágoras era partidario del cálculo matemático para construir la escala, mientras que Aristógenes creía que era el oído el que debía decidir, creándose en la época una muy educada discusión alrededor del asunto. Pero finalmente fue el oído el que prefirió la escala de Pitágoras para la homofonía (melodía sin acompañamiento), que era la música de la época, mientras que la escala de Aristógenes tuvo que aguardar hasta el surgimiento de la polifonía (varias melodías simultáneas) para ser la preferida y, una vez más, en esa elección fue determinante lo que decía el oído: para la música homófona de los griegos sonaba mejor la escala de Pitágoras; pero para combinar sonidos simultáneos de frecuencias siempre diferentes – sin ir más lejos, la música de Bach -, se prefirió la escala de Aritógenes. Entonces nos preguntamos: ¿Acaso todo ello giró más bien alrededor de decisiones arbitrarias, intuitivas, auditivas…?

Pues sí, aparentemente así habría sido. Al parecer, basándose exclusivamente en lo que gustaba o no a sus atentos oídos, decidieron dividir el intervalo de frecuencias entre el sonido “1” (el producido por la cuerda original) y el sonido “2”, o mejor, el “2/1” (el producido por la cuerda de mitad del tamaño de la original y que produce un frecuencia doble) en siete intervalos. Siete; no ocho ni seis. ¿Por qué siete? No se sabe exactamente por qué, pero el caso es que 7 es un número ni grande ni pequeño, de buen augurio y, encima, primo. Sea como sea, el caso es que 7 permite una cantidad suficiente de combinaciones de sonidos para hacer piezas de música todas distintas.

Bien, una vez decidida la división en 7 partes, había que definir ahora dónde deberían caer las divisiones dentro del intervalo fundamental 2/1 (es decir, entre la nota de una determinada frecuencia y la del doble de frecuencia). Debió parecerles lógico y natural (en el sentido de que “está en la Naturaleza”) que esas relaciones que hallaban fuesen las más armoniosas posibles para ser combinadas. Por algún motivo, que aún hoy seguimos tratando de entender, juzgaron como más armoniosas las relaciones 4/3 (relación 1,3333…), 3/2 (relación 1,5), 9/8 (relación 1,125), etc. En la terminología musical esas relaciones se llaman, respectivamente, “cuarta”, “quinta”, “tono”, etc. ¿Por qué esos nombres tan extraños? En seguida lo explicaré. Dividiendo entonces el intervalo 2/1 en relaciones numéricas tales que la separación entre las notas sucesivas fuera más o menos constante (es decir, que no se percibieran grandes saltos entre una nota y la siguiente), dedujeron la escala. Vemos así que todo ello no era tan sólo intuitivo; en realidad estaba gobernado por los números – aunque siempre muy bien controlado por el oído.

Hasta nosotros han llegado solamente dos formas usadas por los griegos de dividir el intervalo 2/1 que hoy, en la terminología musical, se llama “octava”…

¿…Octava? ¿Por qué “octava”? Simple: porque si la división de la escala, del intervalo fundamental, es en 7 partes, eso quiere decir que tenemos una escala de 7 sonidos y, al llegar al octavo sonido, éste tendrá el doble de vibraciones que el que lleva el número 1 de la escala, es decir, suena igual, pero más agudo. En la nomenclatura actual de los sonidos, para llegar hasta la octava del DO, por ejemplo, habrá que pasar por 7 notas: DO, RE, MI, FA, SOL, LA, SI. Y la octava nota es de nuevo el DO. Aclaremos algo más, a propósito: excepto el “tono” y el “semitono” – de los que hablaremos dentro de unos momentos – todos los demás intervalos se llaman de acuerdo a la cantidad de notas que hay que contar desde la fundamental, desde la primera, o sea: “tercera” (se cuentan 3 notas: do, re, mi); “cuarta” (se cuentan 4 notas: do, re, mi, fa); “quinta” (se cuentan 5 notas: do, re, mi, fa, sol); y así en adelante. A la octava nota, lógicamente le llamaremos “octava”.

¡Rayos! – me decía Macluskey, sumergido entre libros, papeles y enciclopedias, cual Fausto tratando de adivinar desde tiempo ha algún secreto místico – cuando recordaba su propio artículo sobre la Sinfonía nº 3, “de las Lamentaciones”, de Heynrick Gorecki,refiriéndose al devastador primer movimiento, cuando él se refería a que cada nuevo pasaje que arrancaban contrabajos, cellos, violas, violines, etc., lo hacían “una quinta” más alto que el pasaje anterior, y allí había agregado que “¡Vaya Vd. a saber qué significará eso!”. Pues ahora me dice que ya lo sabe: para subir una quinta simplemente se trata de multiplicar por 1,5 la frecuencia de cada nota, es decir, comenzar cinco notas más arriba, en la “quinta” nota… Como es informático, pero le gusta mucho la música, se quejó de que… ¡podían habérselo dicho antes!

Bien, volviendo al tema que nos traíamos entre manos, decíamos que hay dos formas de dividir la octava. Ellas son la escala de Pitágoras y la de Aristógenes. Se basan en el mismo concepto, ambas contienen, y en las mismas posiciones, las notas más importantes (las de relaciones 9/8, 4/3 y 3/2). En cuanto al resto de las notas, son muy parecidas, aunque no iguales y, desde luego, en ambas la octava nota tiene el doble de frecuencia que la primera. Viendo ambas juntas, la de Pitágoras es bastante más complicada y parece mucho más natural y sencilla la de Aristógenes:

Así es como se ve siempre la relación entre las escalas… pero a los legos esta figura les deja bastante fríos. O directamente les hace salir huyendo. Así que hagamos unos pocos cálculos y tendremos, para ambas escalas, lo siguiente:

En la primera columna tenemos que la nota de que se parte es DO. A continuación, el resto de notas (Re, Mi…) hasta un nuevo DO que marcaría el inicio de la misma escala una octava más alta. Naturalmente, los griegos no llamaban así a las notas, pero así podemos entendernos más fácilmente.

En la segunda columna está la relación con la que se obtiene la nota siguiente. Es decir, dado un DO con ciertas vibraciones por segundo, obtendremos cuántas vibraciones por segundo (o frecuencia) debe tener el RE siguiente multiplicando la frecuencia del DO por (9/8), o sea, por 1125 Hz, y esto en ambas escalas. Dado un DO de, por ejemplo, 1000 Hz, entonces el RE debe tener 1000 x (9/8) = 1125 Hz. Luego se hace lo mismo con el resto de las notas.

En la tercera y cuarta columnas está la relación que mantiene cada nota con la nota inicial, el “DO” en este caso. Naturalmente, mediante el producto de la relación de la nota anterior por la del intervalo es como se obtiene la nota siguiente. Primero he puesto el método de cálculo y después lo que da el resultado una vez simplificado. Es decir, en la cuarta columna está la relación de la nota de marras con la nota fundamental, la primera, que en nuestro caso es el DO inicial.

Por fin, en la quinta columna he puesto los hercios (la frecuencia) de la nota suponiendo que ese primer DO tuviese 1000 Hz. He elegido esta frecuencia fundamental tan redonda para que simplifique la explicación posterior aunque no se use en la práctica, pues esa frecuencia fundamental de 1000 Hz para el DO no se usa hoy en día en ninguna afinación. El más cercano de los que se usan realmente sería el que se encuentra dos octavas por encima del DO central del piano, que corresponde a 1046,4 Hz. Por si fuera poco, no tenemos la certeza de cómo se afinaba en el pasado (durante el Barroco el LA central podía ser de tan sólo 415 Hz y, durante el siglo XIX todavía no había acuerdo universal sobre la frecuencia del diapasón). Por eso es tan importante entender que lo significativo es la relación entre notas, no el número exacto de hercios de cada una.

Pues bien, si miramos con atención esa relación final entre notas vemos varias cosas:

• Primero, que efectivamente el DO final de la escala tiene el doble de frecuencia que el inicial, cosa que obligatoriamente deben cumplir las escalas para funcionar en la música.

• Segundo, que hay tres notas cuyas frecuencias coinciden en ambas escalas: La nota RE (o sea, la segunda nota), que es un 9/8 del DO inicial, la nota FA (cuarta nota), que está en una relación 4/3 con el DO inicial, y la nota SOL (quinta nota), que está en relación 3/2 con el DO inicial. Y no hay más notas iguales entre ambas escalas. No es que haya mucha diferencia entre ellas, pero la hay. Por ejemplo, un MI según Aristógenes está en una relación simple 5/4 (1,25 veces el DO), mientras que para Pitágoras estaría en una relación más complicada: 81/64 (1,2656 veces el DO). Parecido, pero no igual. Y lo mismo con el LA o con el SI.

• Tercero, que son mucho más simples las relaciones finales obtenidas según Aristógenes que según Pitágoras (que el SI sea 256/243 veces el LA anterior, o bien 243/128 veces el DO original, resulta complicado de afinar y en la polifonía se pueden generar batimientos desagradables al oído). A cambio de eso, según Pitágoras hay sólo dos tipos de separación entre intervalos: 9/8 y 256/243, mientras que según Aristógenes hay tres: 9/8, 10/9 y 16/15.

Pero, como ya dijimos, lo importante, lo realmente importante, es cómo suena todo esto al oído. De modo que para los griegos, que entonaban melodías sin acompañamiento, era obviamente preferible la escala pitagórica por ser más simple. Y, claro está, también nosotros decimos que las escalas tal como las conocemos hoy nos suenan bien al oído, todos hemos oído mil veces cantar o tocar una escala (Do-Re-Mi-Fa-Sol-La-Si-Do) y nos parece que está todo bien, que las notas están perfectamente ubicadas donde están y que la “distancia auditiva” entre cualquier nota y la siguiente es siempre aparentemente la misma… ¿no es así?

Pues no, no es así. Primero que nada, salvo los oídos bien entrenados, casi nadie consigue diferenciar e identificar con facilidad la ubicación de los intervalos más grandes y más pequeños dentro de la escala. Pero es evidente, en ambas escalas – pitagórica o aristogénica – que hay notas que están más cerca entre sí que otras, puesto que la relación entre sus intervalos es diferente, y en algunos casos, muy diferente. Por ejemplo, la escala de Pitágoras tiene dos clases de intervalo: 9/8 (es decir, 1,125) y 256/243 (que es 1,0535, algo menos de la mitad de 9/8). No hay más que mirar los cuadros de arriba para darse cuenta de ello. En cuanto a la de Aristógenes, ocurre lo mismo: entre el intervalo 9/8 (es decir, 1,125) y el intervalo 16/15 (1,0666…): hay también una gran diferencia, pues nuevamente el intervalo pequeño es algo más de la mitad del intervalo grande. Y además hay también una relación de 10/9 (1,1111…), para complicar más las cosas.

Lo que ocurre es que lo que al oído suena perfectamente correlativo oyendo una escala que alguien sepa tocar o cantar, tiene en realidad diferencias muy apreciables en cuanto a la relación entre las frecuencias. Parece que la distancia subjetiva entre el RE y el MI fuese muy semejante a la que hay entre el MI y el FA, por ejemplo, pero en cambio la relación entre las frecuencias de RE y MI es de 1,125 veces según Pitágoras, o de 1,1111… veces según Aristógenes, mientras que la diferencia entre MI y FA es de tan solo 1,0535 veces o de 1,0666 veces, según sea la escala. Eso es la mitad, aproximadamente.

Es de suponer que los filósofos naturales griegos del Siglo VI a.C. se dieron perfecta cuenta de este hecho, pues eran hábiles en sus cálculos, además de tener un oído muy refinado. Casi se podría apostar a que debió ocurrírseles la solución “evidente”: dividir la escala en siete intervalos iguales. No es algo difícil de calcular, pues basta con que el intervalo entre las siete notas fuese la raíz séptima de 2, es decir, 1,1040895… Efectivamente, si la relación entre cada una de las siete notas y la siguiente fuese así – la raíz séptima de 2 -, se seguiría cumpliendo una de las premisas básicas: La octava nota tendría exactamente el doble de frecuencia y la separación matemática entre notas sería perfectamente igual. Claro que, a cambio, tenemos un pequeño problema: no hay una sola nota que tenga una relación “natural” con nada (se acabó el 4/3, el 5/4 y hasta el sacrosanto 3/2, que es la famosa “quinta” alrededor de la que gira todo esto y suele costar bastante entender por qué).

Pues aún hay más: la relación entre notas calculadas con este sistema “igual” queda no sólo muy complicada para afinar, sino que tropezamos con algo casi sobrecogedor: Nunca habrían podido existir las tonalidades que conocemos, jamás habría existido la música modal ni el Canto Gregoriano, no serían posibles aquellos efectos de “punto final” en el discurso musical y no podría haber ningún “acorde perfecto” consonante. Sin exageración ninguna, la historia de la música habría sido completamente distinta si los griegos hubiesen optado por estos cálculos:

Al no tener relaciones naturales, hay que pensar si esta escala sonaría bien, por más perfecta que se la vea en el papel. El oído es logarítmico y, en consecuencia, si escuchamos la escala durante varias octavas seguidas, deberíamos tener la sensación de ir subiendo “peldaños” hasta llegar al punto donde la escala va siendo transportada, una y otra vez, una octava más arriba y tiene el doble de frecuencia que la anterior. Comprobemos si esto es cierto, escuchando una escala formada únicamente de intervalos idénticos:

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

Esta escala – utilizada con frecuencia en la música impresionista (Claude Debussy, por ejemplo) – no tiene 7 notas, sino 6, o sea que el intervalo entre las notas es la raíz sexta de 2. A diferencia de la anterior, esta otra se puede tocar en un teclado con una aproximación suficiente. ¿Pero… alguien percibió “dónde”, en qué nota, se comienza a repetir la escala con el doble de la frecuencia para cada nota? Apuesto a que no. Y lo mismo sucede con cualquier escala cuyos intervalos sean todos idénticos. Comprobémoslo una vez más, oyendo otra escala, compuesta también de intervalos idénticos, pero esta vez la octava queda dividida en 12 intervalos iguales (es la llamada “escala cromática”):

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

Pero es que, además, el oído no necesariamente es completamente logarítmico. La conformación física de las escalas clásicas griegas (llamadas diatónicas) así lo prueba: si dentro de la escala hay notas más separadas entre sí que otras, aunque para nosotros sean peldaños que nos suenen más o menos semejantes entre sí, podremos distinguir el pasaje de una octava hacia la siguiente, si aguzamos el oído lo suficiente:

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

Así que hay que rendirse a la evidencia: las escalas con sus notas separadas de esta forma concreta son las únicas que hacen posible estructurar la música en forma concordante con las cualidades perceptivas del oído. Por eso, tal vez, debió decirse ya en aquella época que “suena bien”.

La consecuencia: en la escala diatónica hay intervalos grandes (entre Do y Re, entre Re y Mi, entre Fa y Sol, entre Sol y La y entre La y Si), e intervalos pequeños, de aproximadamente la mitad que los grandes (entre Mi y Fa y entre Si y Do). Se le llama “tono” a los intervalos grandes y “semitono” a los pequeños. Es decir, entre Re y Mi, por ejemplo, hay un tono de separación, mientras que entre Si y Do o entre Mi y Fa lo que hay es un semitono de separación.

¿Ya está todo aclarado y nos podemos dedicar a componer una cantidad casi infinita de músicas diferentes? Pues… no. Porque aunque las combinaciones de un conjunto de elementos pueden ser muchas, el uso reiterado de esos siete sonidos exclusivamente, acabaría por agotarse y cansarnos tarde o temprano. La solución casi obvia es simplemente poder comenzar la escala por cualquier nota, no sólo siempre por el DO. Así podríamos tener no una única escala basada en DO, sino siete, basándose en RE, en MI, etc., pero no recurriendo a la música modal – que, en realidad, sigue usando siempre los mismos 7 sonidos, según veíamos en el artículo anterior. Aquí, en cambio, se trataría de “transportar” toda la escala a otra altura. Lo único que habría que tener en cuenta es mantener las notas separadas por tonos y semitonos de una manera precisa:

Separadas por tonos: La primera nota de la segunda, la segunda de la tercera, la cuarta de la quinta, la quinta de la sexta y la sexta de la séptima.

Separadas por semitonos: La tercera nota de la cuarta y la séptima de la octava.

Aparentemente será suficiente aplicar las relaciones pitagóricas/aristogénicas que ya conocemos para calcular cada nota y tendremos una nueva escala Mejor dicho, habremos “transportado” la escala adoptando como punto de partida otra nota. Si las relaciones numéricas entre las notas son independientes de la frecuencia inicial (ver la primera figura al comienzo de este artículo), no debería haber ningún problema, ¿no?

¿NO?

Pues sí. Hay problemas, y muchos. Veamos cómo quedarían ambas escalas si partimos como nota fundamental no del DO, sino del RE:

 

Si nos fijamos en las columnas de la izquierda (las mismas que había antes en la escala de DO), no ocurre nada extraño. Todas las relaciones son posibles, dan relaciones naturales, como 3/2, 5/4, etc. Pero, claro está, ahora en la columna de la frecuencia real de cada nota – que he comenzado con la frecuencia que tenía el RE en la escala de DO que veíamos antes – se supone que todas las notas tendrán que sonar igual en la escala que empieza en RE. Así que he puesto como base del cálculo 1125 Hz, que era la frecuencia que le correspondía al RE en la escala de DO. Se calcula después la frecuencia de cada nota, pero… veamos qué ha sucedido.

Si colocamos al lado cuáles son las frecuencias de cada nota que calculamos antes según la escala de DO, ya tenemos aquí el primer problema. Vemos que, en ambas escalas, ciertas notas coinciden (además del RE, por supuesto): el SOL y el SI, en ambas escalas, y el MI y el LA, en la de Pitágoras. Pero el resto de notas no, no coinciden. En la escala de Aristógenes no coinciden el MI ni el LA, aunque la diferencia es muy pequeña, debido a la diferencia entre los “tonos grandes” (de relación 9/8) y los “tonos pequeños” (de relación 10/9), pero en cuanto al FA y el DO… ahí la diferencia es muy grande, más o menos la mitad de lo que debería ser.

Fijémonos ahora, por ejemplo, en el DO de la escala de Aristógenes: Calculado desde la escala de DO, le tocaría tener 2000 Hz, mientras que calculado desde la escala de RE, le tocan 2109 Hz. Esa diferencia, 109 Hz, es mucha, y de hecho es muy parecida (125 Hz) a la que hay entre el SI y el DO calculado en la escala de DO. Y lo mismo le pasa al FA.

Si lo recordamos bien, la diferencia entre SI y DO era lo que habíamos llamado un “semitono”, por ser aproximadamente la mitad de un “tono” (como el que separaba a DO y RE o a RE y MI). O sea, que la diferencia entre el DO calculado según la escala de Do (2000 Hz) y el DO que resulta calculado según la escala de Re (2109 Hz) es también, aproximadamente, un semitono.

Entonces, parece que no queda otra opción que “inventar” alguna nota nueva, una que estaría entre el DO original calculado según la escala de Do (2000 Hz) y el DO que resulta si comenzamos la escala en el RE (2109 Hz). A este nuevo DO de 2109 Hz, un semitono más agudo que el DO original, lo llamaremos “Do Sostenido” – en la escritura musical se usa el símbolo # , es decir, Do# -, y habrá que darle carta de naturaleza y considerarle como una nota más, totalmente válida. Y lo mismo habrá que hacer con el FA: ese nuevo FA de 1423 Hz que aparece en la escala de Re, separado por el FA de la escala de Do (1333 Hz) por otro semitono, unos 90 Hz, hay que considerarle también, y le llamaremos “Fa sostenido” (Fa#). En el teclado, que seguro que has visto mil veces, estas nuevas frecuencias se ven así:

Ya vamos viendo para qué sirven las teclas negras del piano. Y, claro, ya no tenemos 7 notas originales, sino 9. Si queremos tocar una música en la escala de Re, y queremos que lo que compongamos suene afinado (para lo que es preciso, no lo olvidemos, que la separación entre las notas tercera y cuarta, y entre las notas séptima y octava, sea de un semitono, es decir, la mitad que en el resto de las notas), entonces en lugar de tocar un Do hay que tocar un Do sostenido en su lugar. Si tocáramos un Do en su lugar, sonaría fatal y lo mismo pasa con el Fa: hay que sustituirlo por un Fa sostenido, por las mismas razones.

Pero esto no acaba aquí. Miremos de nuevo el teclado. ¿Para qué sirve el resto de las teclas negras? Buena pregunta. Si en lugar de tomar como comienzo de la escala el RE (es decir, esos 1125 Hz) comenzamos por cualquier otra nota, nos pasarán cosas similares, y necesitaremos nuevos sonidos intermedios. Veamos, por ejemplo, lo que pasa con la escala de Mi, la que toma como comienzo de la serie el MI (1265 ó 1250 Hz, según la escala):

Ahora, con la escala original del DO sólo coinciden (además del propio MI) el LA y el SI. Las dos notas que habían aparecido nuevas con la escala de Re (DO sostenido y FA sostenido) se conservan con sus mismas frecuencias (al menos en la escala de Pitágoras: DO sostenido con 2135,7 Hz y FA sostenido con 1423,82 Hz, pero en la de Aristógenes ni siquiera eso, debido a que los tonos son de dos clases distintas: 9/8 y 10/9). Y han aparecido dos notas nuevas: el SOL sostenido, más o menos a medio camino, o sea, un semitono, entre el SOL y el LA (tiene 1601,8 Hz ó 1562,5 Hz, según sea la escala utilizada, en vez de 1500, que es lo que SOL tenía en ambos casos), y el RE sostenido, también a medio camino (un semitono) entre el RE y el MI (tiene 2402,7 Hz ó 2343,75 Hz, en lugar de los 2250 Hz que tenía en ambas escalas de Do). Esto se ve así en el teclado:

 

Y si seguimos haciendo lo mismo con todas las notas, se llega a la división de la octava del piano en 12 teclas (7 blancas y 5 negras). ¿Con eso se terminaron finalmente los problemas?

Lamentablemente, no. Si desarrollamos los cálculos a partir del FA – ya habíamos hecho la prueba con el RE y el MI, ahora le toca al FA -, nos encontraremos con otra novedad: si empezamos la escala por el FA (fa-sol-la-si-do-re-mi-fa) no tenemos ninguna nota disponible para subir. ¿Cómo puede ser eso?

Veamos en primer lugar cómo quedaría nuestro esquema de frecuencias si desarrollamos los cálculos a partir del FA:

Fijémonos ahora en la frecuencia que le toca a la nota SI para mantener la estructura de tonos y semitonos: Tanto en la escala de Aristógenes como en la de Pitágoras, debe tener 1777,7777 Hz, mientras que en la escala de DO tenía 1898,4375 Hz, en una, o 1875, en la otra. O sea, en la escala de FA, el SI tiene menor frecuencia (unos 100 Hz menos, o sea, un semitono) de lo que debería tener… y esto es, efectivamente, una novedad. Hasta ahora nos habíamos encontrado con notas cuyas frecuencias eran mayores que las que deberían tener en la escala de DO, y habíamos dicho que esas nuevas notas las llamábamos “sostenido”, por ejemplo, el RE#, o el SOL#, que eran, respectivamente, un semitono mayores que el RE o el SOL originales.

Pues bien, en la escala de FA este truco no sirve: el pseudo-SI que aparece no puede ser un SI#, porque la frecuencia no es un semitono mayor que el SI, sino que es un semitono menor… Y aquí es donde entran los “bemoles”, que es el término usado en la música cuando hay que reducir la frecuencia de la nota. Efectivamente, el SI de la escala de FA es un SI bemol, que es un semitono menor que LA-SI, pero… atención: SI bemol no es lo mismo que LA sostenido, aunque ambas notas (el LA sostenido y el SI bemol), están por cierto entre el LA y el SI, aproximadamente a un semitono de distancia de ambas. Y, claro está, “aproximadamente” no es lo mismo que “exactamente”.

Detengámonos un momento en este detalle, porque cualquiera preguntaría: ¿Importa mucho la forma como se escribe, si las frecuencias están bien calculadas? ¿Por qué no proseguir con el método de aumentar la frecuencia del sonido que sea, si hace falta, en lugar de invertir el proceso comenzando ahora a bajar frecuencias? O sea, ¿por qué no se puede escribir fa-sol-la-la# -do-re-mi-fa, completando 7 sonidos, aunque se omitiese el nombre de la nota SI? Naturalmente, un músico experimentado discutiría tal cosa en seguida y tendría sus razones. Pero nada de esto es tan sencillo, ni de un lado ni del otro de la discusión.

Lo que ocurre es que el intervalo La-La# es un semitono cromático – del que no habíamos hablado todavía-, y lo que necesitamos es un semitono diatónico, que es el natural de la escala. ¿Qué es un semitono “cromático”? En general los músicos están tan habituados a usarlo, y a aceptar la definición que dan los textos, que muy rara vez se preguntan de dónde viene y para qué sirve.

Primero que nada, sepamos que el único indicio acerca del uso que los griegos hicieron del semitono, no concuerda en nada con lo que hoy entendemos por “cromático”. Los griegos decían que añadir algunos sonidos que no pertenecían a la escala diatónica le daban un cierto “color” (cromos) a la música – y ahí nace la etimología del término. Pero ese color, o “cromatismo”, era en base a intervalos mucho menores que el semitono diatónico. Entonces, aquellos intervalos “cromáticos” no eran semitonos o, mejor dicho, no eran “medios” tonos.

Sigamos. En los libros donde se estudia la acústica musical, “aparece” la relación … (o sea, ) para definir al semitono cromático. ¿De dónde sale eso? En realidad se trata de un cálculo hecho a la fuerza para simplificar el resultado de otro cálculo: el que permite transportar la escala íntegra a frecuencias más altas o más bajas. Ya lo veremos dentro de un momento. Veamos antes que, según el cálculo forzado del semitono cromático que hemos referido justo más arriba, si seguimos con nuestro ejemplo de la nota LA tendríamos que en la escala de DO de Pitágoras, por ejemplo, tenemos un LA de 1687,5 Hz que, si lo elevamos un semitono cromático calculado de dicha forma, resultará Hz, que sería supuestamente el LA# . Lo dejamos anotado aquí, para volver luego de lo que veremos a continuación.

Ahora vamos al meollo de la cosa. ¿Qué le ocurre a la escala de SI, si hacemos lo mismo que hasta ahora hemos hecho?, es decir, calcular las notas resultantes tomando como partida la frecuencia de la nota SI en la escala de DO (1898,4375 Hz, en nuestro ejemplo). Parecería no tener nada que ver con eso del semitono cromático, pero veámoslo:

 

Si nos fijamos en la escala de Pitágoras, por ejemplo, vemos que a la nota LA le corresponderían 3604,06494 Hz (es la celda sombreada; en la de Aristógenes ocurre lo mismo, por cierto). Como esa nota es de la octava siguiente, para ver qué frecuencia le correspondería en nuestra octava original (la que va de 1000 a 2000 Hz), hay que dividir por dos su frecuencia, y nos queda exactamente 1802,03247 Hz que… era el resultado que habíamos anotado más arriba. Y, obviamente, no es lo mismo que los 1777,77 Hz que nos salían para el SI bemol calculando desde la escala de FA, pero hay algo más: el SI bemol resulta de calcular la escala de Fa, mientras que el LA sostenido resulta de una relación entre escalas, en este caso la de Fa y la de Si.

De acuerdo a esto que terminamos de ver, una definición coherente del término “semitono cromático” sería que es el intervalo que se produce entre notas de una escala diatónica respecto a notas de otra escala diatónica diferente, cuando coinciden los nombres de las notas.

Posiblemente esto rechine muy fuerte a cualquiera que sólo haya oído hablar del semitono cromático como “dos notas de igual nombre separadas por un semitono mediante alteración de una de ellas” – bajo el dudoso supuesto de que, dicho así, sería comprensible para cualquier persona –, pero la realidad es que el semitono cromático, como tal, no existe. Existe solamente cuando una escala se relaciona con otra, y solamente así, pues cualquier sonido que lo forme se origina únicamente en el conjunto de escalas diatónicas. Por lo tanto, contrariamente a lo que comúnmente se cree, no sirven para “crear” las escalas necesarias en todas las tonalidades.

¿Para qué sirven, entonces? Los compositores los utilizan, en la música tonal, para salir de una tonalidad y pasar a otra. Más claro: introducen en una escala notas que pertenecen a otra escala y, de esa manera, combinan las diferentes tonalidades. También los utilizan para ornamentar las melodías – en forma parecida a como ya lo hacían los griegos – sin salir de la escala que están usando. Y a la escala que se toca usando las 12 teclas del piano le llaman “escala cromática”, pero en realidad contiene todos los sonidos de cualquier escala diatónica posible de tocar en el piano o cualquier otro instrumento de entonación fija. Claro, esto último es por demás evidente, aunque ahora sabemos por qué es así…

Sigamos con el análisis como veníamos haciendo.

¿Cuánto mide la diferencia entre ambos sonidos (entre el LA sostenido y el SI bemol)? El semitono diatónico, LA-SI bemol, según Pitágoras se forma en proporción de 256/243 = 1,05349794… (ó 16/15 = 1,066666… según Aristógenes). La diferencia con el LA sostenido es poca, tan sólo de , algo más de un 1% superior. Este pequeño intervalo, que marca la diferencia entre el sostenido y el bemol – para éste o cualquier otro caso semejante – se llama una “coma” (viene a ser aproximadamente la cuarta parte del semitono diatónico) y es perfectamente audible.

Los griegos ya lo sabían, pero como todavía no tenían el problema de las tonalidades ni de los instrumentos de teclado, nunca lo vieron de esta manera:

 

O sea, no tenían ese problema de hacer encajar en el espacio de una octava TODOS los sonidos que hiciera falta para tener la escala transportada a cuantas frecuencias quisiesen.

Claro que en un teclado la “coma” no importa, porque sólo hay una tecla negra entre el LA y el SI, por lo que ahí el LA sostenido y el SI bemol coinciden a la fuerza. Pero para un instrumentista de arco (un violinista, por ejemplo), o para un cantante, la afinación del sostenido es diferente de la del bemol: todo consiste, en el caso de un violinista, en tomar la presa un milímetro más arriba o más abajo para ejecutar uno u otro sonido… El caso es que si un violinista toca un bemol en vez de un sostenido, cualquiera que tenga buen oído se dará cuenta de la desafinación. Los pianistas no tienen esos problemas – pero los violinistas a veces sí, cuando tocan acompañados por un pianista – porque el piano usa las mismas teclas… y no podemos entender este problema si miramos solamente el teclado.

Volviendo a la escala de FA, y resumiendo, en la notación musical este nuevo sonido se llama “SI bemol” y difiere una “coma” del “LA sostenido” en la escala de Fa.

Ahora bien, ese nuevo sonido que hace falta, ese SI bemol, ¿necesitaría también tener su propia tecla en el piano? Por supuesto que sí, si queremos que no suene desafinado… pero con esto hay nuevos problemas a la vista.

En este enredo, que no proseguiré desarrollando para no hacer interminable este ya largo artículo, sólo diré que todas las observaciones hechas hasta ahora para los “sostenidos”, también se cumplen para los “bemoles”, y por eso siguen agregándose más y más notas. Pero esto significa, ni más ni menos, que si para los sostenidos necesitábamos ir agregando correcciones de afinación, una por una, hasta alcanzar un total de 12 sonidos dentro de la octava, otro tanto ocurrirá con los bemoles que, uno a uno, irán agregándose hasta totalizar otros 12 sonidos que no coinciden con los anteriores. Entonces, ¿alcanzaría con tener 24 teclas y se habrían terminado los problemas? Quizá con un poco de ingenio…

Pues no, tampoco. A causa de que la polifonía adoptó la escala de Aristógenes, y no la de Pitágoras, ahora tenemos que lidiar con la diferencia entre dos clases de tonos: el “tono grande” (10/9) y el “tono pequeño” (9/8), pero no solamente para una sola escala, sino para todas las escalas posibles y las “comas” que de un conjunto así formado puedan surgir. Y esa es una complicación extraordinaria que los fabricantes de instrumentos de teclado no tuvieron más remedio que solucionar, siglos más tarde, con ayuda del cálculo matemático (el “temperamento igual”, deducido de la raíz 12 de 2, y que corresponde exactamente a las 12 teclas por octava en el piano). Ésta es la razón de que hoy, ya solucionado ese problema, el teclado sea así como se lo ve; pero, aun así, la escritura musical debe mostrar la diferencia para que sea una expresión coherente de la realidad física: nada de creer que se puede simplificar anotando “FA” cuando debería ser “MI sostenido” – sólo porque en el teclado “MI sostenido” y “FA” se tocan en la misma tecla -, lo mismo que “SOL bemol” y “FA sostenido”, etc. En la notación musical correspondiente a las diversas escalas no es lo mismo, y debe signarse correctamente en cualquier caso que corresponda.

Entre los varios intentos de clarificar todo esto poniéndolo al alcance de cualquier músico, hay un caso que es quizá el más conocido. En el año 1679 el teórico y compositor ruso Nikolai Diletski escribía el que se considera primer tratado de composición en la historia, y allí aparece por primera vez el diseño del “Círculo de Quintas”, que se volvería célebre al permitir visualizar, más al alcance de los músicos – de los legos, no tanto… o nada – el fenómeno del que venimos hablando:

 

 

El caso es que aquí aparece un nuevo problema: como el círculo en realidad no se cierra, pues “SI sostenido” no es exactamente igual a “DO” (aunque difieran solamente en una humilde coma) y lo mismo ocurre entre “SI” y “DO bemol”, la proyección podría proseguir indefinidamente, y se convertiría en una espiral.

Pitágoras no conocía el círculo de quintas ni el temperamento igual, así que su preocupación fue otra: descubrió que 12 quintas no producen 7 octavas exactas. El resultado final era un sonido “casi” igual a la octava N° 7 del sonido fundamental… pero no era igual. La diferencia es… tan sólo una coma, claro (1,0136). Veámoslo en el gráfico siguiente:

 

Tomamos una nota inicial arbitraria, digamos de 100 Hz por comodidad (esto sería casi, casi un SOL en la afinación actual), y le aplicamos doce quintas consecutivas, es decir, multiplicamos doce veces la frecuencia inicial por 3/2, es decir, por 1,5. La duodécima quinta tendría así 12,974,634 Hz. Esto está calculado quinta a quinta en la columna izquierda del gráfico.

Pero, claro, si calculamos qué frecuencia debería tener la séptima octava de la misma nota inicial (en la derecha del gráfico), llegaremos a que debería tener 12.800 Hz, que no es lo mismo que 12,974,634. La diferencia, de 174,634 Hz, es exactamente una coma (12.974,634 dividido por 12.800 da exactamente 1,01364…, es decir, la relación de intervalo que define una coma, como hemos visto antes).

Ya van varias veces que aparece la “coma”, inesperadamente, como surgiendo de la nada … En realidad, la aparición de la “coma” es evidente si se quiere hacer cuadrar siete octavas con doce quintas calculadas cada una como (3/2) de la nota anterior. En efecto, tras multiplicar la frecuencia F de la nota inicial doce veces consecutivas, tenemos un valor final de . Por otra parte, para obtener siete octavas consecutivas hay que multiplicar por 2 siete veces la frecuencia F de la nota inicial, lo que dará un valor final de 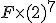. Si ahora queremos conocer la relación entre ambas notas finales, basta con dividir el primer valor por el segundo; simplificando, las F’s desaparecen al estar en numerador y denominador a la vez, y obtenemos un valor final de  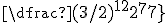, o lo que es lo mismo, , es decir: . El resultado final es el famoso 1,0136432… que es precisamente el valor de la coma musical.

Para nosotros – en nuestra escritura musical -  es la diferencia entre SI# y DO  o entre SI y DO bemol, y podemos omitir la coma y cerrar a la fuerza la espiral, transformándola en un círculo mediante la división de la octava en 12 semitonos iguales, o sea, mediante la raíz 12 de 2. Pero para Pitágoras era inadmisible que la frecuencia de un sonido que debería ser un múltiplo de la frecuencia de la nota fundamental no lo fuese.

Pitágoras no logró solucionar este problema satisfactoriamente, ni siquiera mediante una solución fácil que halló, y luego la veremos, pero sí se anticipó a la época descubriendo que, si se hacía un encadenamiento de 12 quintas, era posible dividir la octava en 12 semitonos – sí, ya en aquellos tiempos – pero, es preciso aclararlo, esa era la llamada “afinación pitagórica” y no la de la escala cromática actual deducida de la raíz 12 de 2.

 

La herencia

Consiguieron enriquecer notablemente la cantidad de sonidos disponibles para la música partiendo de tan sólo 7 notas para dividir la octava, de manera que resultasen combinaciones que satisficiesen las cualidades de percepción de los sonidos naturales por el oído humano. También crearon el “género cromático”, precisamente porque enriquecía el “género diatónico” con sonidos cuya afinación no coincidía con los propios de la escala. A la vez, utilizaron las posibilidades de los sonidos que diferían entre sí una “coma”, creando el “género enarmónico” – o enharmónico – y esta denominación se mantuvo hasta hoy cuando decimos que SI sostenido es “enarmónico” de DO, que FA sostenido es enarmónico de SOL bemol, etc. Y todo ello en base a un solo intervalo como base de cálculo: 3/2 , ó “quinta justa” – como la llaman los músicos.

El poder que aquella estructura completa llegaría a tener sobre la música sería enorme. La causa está en una capacidad evidente para satisfacer al oído. Una mera secuencia de acordes perfectos que estén en relación sucesiva 3/2 se escucha como un conjunto armonioso, a pesar de que el trozo musical que resulta no está – paradójicamente – en ninguna tonalidad. Escuchémoslo:

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

 

Pero una parte de la historia se perdió

Ignoramos mucho acerca de hasta dónde llegaron los conocimientos de acústica en la antigua Grecia. Se perdieron importantes testimonios escritos de aquella civilización y, decíamos al comenzar, lo que hoy se hace es más bien una reconstrucción basada en los pocos documentos que permanecieron luego de la invasión del Imperio Romano a la Hélade. Hoy en día se conservan tan sólo alrededor de sesenta fragmentos de músicas griegas, incompletas, en papiros hallados en Egipto.

Casi exclusivamente sobre la base de estas únicas fuentes conservadas, todavía hoy se prosigue tratando de descubrir cuánto sabían o ignoraban los griegos con respecto a las propiedades del sonido, y cómo razonaban en realidad. Entre las varias conclusiones contradictorias que existen al respecto, quizá la más importante sea la duda acerca de si conocían, o no, el fenómeno de la serie armónica. Se supone que no, pero parecería muy poco lógico ser contundente, afirmando que no, en vistas de la extrema elaboración de la teoría física de la música que les caracterizó.

La historia de la relación entre la música y las ciencias exactas es algo incierta. Esa historia sólo nos cuenta que a partir del momento en que la civilización occidental fue retomando el camino del conocimiento científico, mientras la Edad Media iba quedando atrás, aparecieron investigadores como Zarlino, en el siglo XVI, y más tarde d’Alembert, siendo éste quien ya en el siglo XVIII definió de manera precisa la relación entre la “altura” de un sonido y su frecuencia, afirmando que los sonidos naturales no son puros, sino complejos, quedando así definida la forma de entender los armónicos por la amplitud de la onda. Más tarde, ya hacia el siglo XIX, Fourier mostraría la forma de representar cualquier curva periódica por superposición de ondas sinusoidales. El teorema de Fourier transformaría el fundamento del análisis de los armónicos, la relación entre consonancia y disonancia, los batimientos disonantes, y varios otros conceptos musicales aparentemente muy alejados de las matemáticas, para no hablar de Helmholst y sus teorías acerca de la percepción del sonido, que serían consideradas por compositores como el gran Nikolai Rimski Korsakov para escribir su célebre Tratado de Orquestación.

Lo que diré a continuación es especulativo, pero no imposible, ni tampoco sería la primera vez que habría ocurrido: un descubrimiento puede ser un redescubrimiento en realidad. Resulta difícil creer que algo tan relativamente fácil – y hasta casual – de producir, como es hacer sonar un armónico natural en una cuerda, no hubiese despertado por lo menos la curiosidad de científicos de la talla de Pitágoras o Aristógenes, así hubiese sido tan sólo para saber por qué el timbre era diferente. ¿Nunca ocurrió, ni por casualidad, que una cuerda en vibración fuese rozada en algún punto y produjese ese sonido tan característico e inconfundible? No hay pruebas de que algo así haya ocurrido. No las hay, pero sí sabemos, en cambio, que existían instrumentos de cuerda y que esos sonidos podían producirse si se hubiese querido.

Entonces… hay una pregunta que viene casi sola.

Si creemos que los griegos no sabían nada de armónicos, pero de todos modos pudieron deducir todo un sistema explicable por la ordenación de los armónicos, ¿cómo lo justificaremos? Mediante conocimientos actuales, se ha expuesto de muchas formas la justificación de las relaciones armónicas que originaron la escala diatónica. Aquí mismo hemos analizado una de ellas. Pero, ¿fue casual que la relación armónica 3/2 fuese el fundamento de toda la teoría? Vale la pena reducir todo lo dicho a la sola expresión del axioma de Pitágoras:

“Cualquier intervalo puede expresarse como una combinación de un número mayor o menor de quintas justas”

El axioma se cumple para cualquier intervalo diatónico que sea. Por ejemplo, fa-do-sol-re-la-mi es una secuencia de cinco quintas, lo cual hace que entre la primera nota y la última de la secuencia se forma el intervalo fa-mi, que es una “séptima” (7 notas), pero también se puede reducir a un semitono si invertimos el orden (mi-fa), y he ahí el semitono diatónico. Todos los intervalos de la escala surgen a partir del axioma pitagórico, sin excepción, y el cálculo así lo comprueba.

Ahora bien, aunque Pitágoras y Aristógenes partieron de un mismo axioma, lo encararon en formas distintas. Para la visión que la posteridad tendría de la teoría de la música, esto tendría consecuencias a largo plazo.

Aristógenes creó una escala donde los intervalos son afinados exactamente según la serie de armónicos. Por esta razón, su escala se llamó también “de la justa entonación” o “de los físicos”. Pero la simetría no es perfecta, a causa de la distribución en tonos grandes (9/8) y pequeños (10/9), hecho éste que introduce variables muy complejas al desarrollarse la proyección hacia los sostenidos o los bemoles.

Pitágoras, por su parte, crearía una escala donde la disposición de tonos y semitonos es la misma, pero los tonos se forman todos en relación 9/8. No existen tonos distintos entre sí. Los semitonos, a su vez, se forman potenciando los armónicos  o sea, . Esta escala no resulta afinada en coincidencia con los armónicos, pero le permitió a Pitágoras corregir lo suficiente la 12ª quinta y absorber íntegramente la coma que aparece en la 12ª quinta. Claro, el precio de esta conquista fue alto. Cuando se tocan a la vez las dos notas del intervalo de quinta así corregido, se producen batimientos bastante fuertes y se oye una especie de “aullido” que le ganaría el apodo de “quinta del lobo”, apelativo que tanta gracia hace a Macluskey (para Macluskey, una “quinta del lobo” siempre había sido un terreno rústico habitado por cánidos salvajes…). Sin embargo, en un principio se prefirió usar esta escala, pues se la consideró más favorable a la melodía. ¿Por qué favorecía a la melodía? Como la escala de Aristógenes tiene tonos desiguales, se decía que daba una cierta sensación de “desafinación” (¿no es esto asombroso, estando afinada según los armónicos?), mientras que la de Pitágoras no tenía ese inconveniente al ser iguales entre sí todos los tonos.

Tamaño rompecabezas, en su conjunto, demoraría más de mil años hasta llegar a la solución de todos los problemas, mediante una afinación basada en la escala de Aristógenes, pero dividiendo el intervalo de 8ª (relación 2/1) en 12 partes iguales, o sea, usando una relación entre notas de la raíz 12 de 2. Éste es el sistema de afinación que terminaría imponiéndose. Permite suprimir las diferencias de una coma, se puede cerrar finalmente el círculo de quintas y la quinta del lobo desaparece. Eso sí: no permite la entonación exacta de ninguna escala diatónica. Véase su comparación con, por ejemplo, la escala de Aristógenes:

 

Efectivamente, las notas son muuuy parecidas… pero no son iguales. Por ejemplo, la nota Sol, que al ser la quinta justa de Do debería estar en relación 3/2 (o sea, 1,5), debería tener 1500 Hz pero en realidad tiene 1498 y fracción. Sí, sólo son un par de míseros hercios… Pero ahí están. Y así con todas las notas, salvo el Do, claro.

Antes comenté que Pitágoras pudo tener al alcance de su mano llegar a esta solución de forma sencilla y natural, y eso pudo ser precisamente a partir del cálculo de la coma que vimos antes. Pero no fue así.

Y… ¿de qué manera pudo solucionarlo? Si recordáis, la coma aparece al intentar cuadrar dos cifras que no cuadran: doce quintas con siete octavas, es decir, con , lo que da origen a ese 1,013… de diferencia, que es la coma. Entonces una solución sencilla podría ser simplemente… ¡hacer que cuadren las dos cifras! ¿Cómo…?

Macluskey – que lamentablemente no vivió en la época de Pitágoras – plantea la solución: Manteniendo, por ejemplo, que cada nota de una octava tenga el doble de frecuencia que la misma nota de la escala anterior (es decir, manteniendo el correspondiente a las siete octavas, que son 524.288). Entonces habría que buscar una relación r entre quintas tal que cumpla que 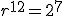. Así de simple. Y si forzamos a que ese r fuese de la forma (r=x/2), quedaría , es decir, simplificando, que . Si obtenemos ahora el valor de x, que es la raíz duodécima de , eso da… caramba: 2,99661415…, ¡casi casi 3!

Es decir, si Pitágoras hubiera calculado sus quintas no como 3/2, sino como 2,996614/2, la posteridad se hubiera ahorrado todo el lío subsiguiente, o al menos una buena parte. Además, puedo aseverar sin temor a equivocarme que, por muy perfeccionados que fueran los métodos griegos de medición en el Siglo VI a.C., no estaban en condiciones de distinguir entre una cuerda de longitud 3,000000 y otra de longitud 2,996614, puesto que apenas se diferencian entre sí en una milésima (sólo en los dos o tres últimos siglos se ha podido realizar la hazaña de medir una magnitud con tal precisión), por lo que ni se hubieran enterado…

Bien, el caso es que si usamos ese valor para recalcular el círculo de quintas igual que lo hicimos antes, pero esta vez usando una nota inicial de 1000 Hz – ya veremos por qué -, tenemos lo siguiente:

Lo que aquí he hecho es usar para calcular las quintas sucesivas la relación (2,996614…/2) en lugar de la relación “natural” (3/2), y luego reconducir la nota resultante a la octava “primigenia” entre 1000 y 2000 Hz, dividiendo el valor resultante por 2, por 4, por 8, etc. ¿Qué tenemos, entonces? Pues… ni más ni menos que las notas correspondientes a la escala de temperamento igual, las mismas que vimos en el cuadro anterior calculado mediante la raíz duodécima de dos. Podéis comprobarlo.

Es con este truco como se ve claramente cómo el círculo de quintas “genera” las doce notas de la escala; si siguiéramos generando quintas sucesivas a partir de la doce, sólo conseguiríamos repetir una y otra vez el mismo ciclo de notas: DO-SOL-RE…FA-DO. Pero, ojo, si usamos el “natural” (3/2) en lugar del “artificial” (2,9966../2) como generador de quintas, entonces esto ya no se cumple: una vez recorridas las doce primeras quintas, empiezan a aparecer comas y más comas de diferencia entre notas sucesivas, que a cada ciclo consecutivo se vuelven más y más diferentes, generando en realidad, como antes dije, una “espiral de quintas” más bien que un círculo… Y, otra vez, vamos de cabeza al tremendo lío de las tonalidades.

Quizás esta pequeña digresión haya ayudado a entender mejor el círculo de quintas, y su utilidad, visto con la óptica del “temperamento igual”. Pero hay algo más.

¿Qué entendemos exactamente por “entonación justa”? Lo que esto plantea es nada menos que lo siguiente. Estamos acostumbrados, desde hace más de dos milenios, a creer que la entonación justa de la escala diatónica es exclusivamente la calculada por los griegos antiguos, pasada después a la escritura moderna en el pentagrama con notas alteradas, cuando en realidad habría bastado con partir de una quinta cuya relación fuese 2,996615/2 para que todas las escalas fuesen de entonación justa… aunque quizá hoy día cueste bastante entenderlo.

Pero en cualquier caso, por supuesto que hubo – y todavía hay – grandes detractores de la solución del temperamento igual, donde cualquiera de los 12 sonidos puede ser la nota fundamental de una escala, pero donde ninguna escala resulta afinada como debería ser. Entonces – cualquiera lo preguntaría -, ¿están de una vez realmente solucionados todos los problemas? ¿Acaso será la secuela de algún error arraigado que, todavía inadvertido, proviene de la antigüedad?

No, no es así. Si queremos que el punto de partida sea una relación 3/2 exacta que, por otra parte y no se puede negar, es la que la naturaleza produce en la serie armónica,  ocurre que no puede existir ninguna división de la octava que permita la exactitud absoluta para más de una sola escala diatónica por vez. Sí, sólo una escala por vez. Si queremos la escala de DO, alcanza con 7 sonidos; pero si queremos que la escala comience en el RE, sin cambiar el orden que debe haber de tonos y semitonos, entonces necesitaremos dos sonidos adicionales, que son el FA# y el DO#. En consecuencia, si la música pide usar ambas tonalidades, deberá haber nueve sonidos disponibles dentro de la octava. Y esa ordenación permitiría tocar tan sólo esas dos escalas con exactitud, y ninguna más. Se ha calculado que, para poder usar a voluntad todas las escalas diatónicas posibles, y cada una en su entonación justa, habría que disponer de no menos de 90 sonidos dentro del ámbito de una octava. Y, aun así, habría que tolerar algunas inexactitudes perceptibles por el oído.

Visto de esta forma, el problema es mucho más complejo de lo que al principio puede parecer, especialmente si pensamos en un teclado. El problema ya lo veía Gioseffo Zarlino en 1558 cuando, sobre la base de la escala de Aristógenes, diseñaba un teclado enarmónico de 19 teclas por octava que, por supuesto, era, aun así, insuficiente.

 

Quizá haya una pregunta final rondando insistentemente en este momento: ¿No habrá alguna posibilidad de hallar un límite, en caso de seguirse desarrollando la “espiral”, donde todas las diferencias se compensen recíprocamente, lo cual permitiría construir un sistema sonoro perfectamente exacto y equilibrado? La respuesta es negativa. Como tantas veces se comprueba en la Física, lo que el ser humano considera como un desequilibrio es en realidad una cualidad de la naturaleza. En este caso, el cálculo logarítmico es el que puede expresar con coherencia la ordenación de las frecuencias para el conjunto de armónicos de una fundamental. No existiendo dos armónicos idénticos entre sí, porque no pueden existir dos frecuencias idénticas en una función logarítmica, definitivamente no existe un límite posible.

Meditando un poco en lo que sabemos (y lo que no sabemos, pero nos preguntamos) acerca de cómo era la música en la antigua Grecia, hay una cuestión sobre la que no existe información alguna y sería hora de llamar la atención sobre ella. En la antigua Grecia la coma era considerada en la práctica musical y se respetaba la diferencia sutil de afinación. Entonces, ¿para qué querrían cerrar el “círculo de quintas”, que es un diagrama de la era moderna, y que, además, refleja conceptos de cómo entendemos actualmente la tonalidad? Si nos atenemos a la arqueología, no hay evidencias de que la música de los griegos hubiese tenido necesidad alguna de clausurar la proyección de quintas.

Por cierto, la escala de Pitágoras permite absorber la “coma” y cerrar la proyección, pero también hay un detalle constantemente esquivado al enfrascarnos en explicar toda la teoría desde el punto de vista del círculo de quintas: tampoco hay ninguna prueba arqueológica acerca de que hubiesen conocido el “efecto quinta del lobo“. Posiblemente esa prueba no exista, porque su música no necesitaba unir las “dos puntas”, siendo que desconocían lo que hoy entendemos como “tonalidad”, es decir, un sistema cerrado y limitado por una “enarmonía” para obtener un conjunto fijo de escalas diatónicas idénticas a diferentes alturas.

Para aquellos antiguos músicos no existían bemoles ni sostenidos. Lo que hoy entendemos por “modulación” (el pasaje de una tonalidad a otra), no tenía el menor sentido, porque se referían al uso de los “modos” de una misma escala. Tampoco entendían la “armonía” en el sentido moderno de la música, y si alguna vez usaban sonidos simultáneos (como “audacias”) lo sabemos solamente a través de las palabras de Platón, que decía que “La lira debería utilizarse junto con las voces, el músico y el pupilo creando al unísono” pero añadía que podía ser “con heterofonías bordadas por la lira”.

 

En conclusión

Mirando el teclado para aprender la teoría es como muchos estudiantes de música se han confundido y siguen confundiéndose. Para empeorar las cosas, en casi todos los libros de teoría musical se enseña, por ejemplo, que “para escribir la escala de Fa se debe bajar el SI un semitono cromático”, o bien, que para anotar la escala de Sol hay que subir el FA un semitono, también “cromático”, etc., lo cual está muy mal expresado, y todavía más: la mayoría de los profesores dirían por qué no puede ser así, y que no hay otra manera de explicárselo a los alumnos. Pues bien, la explicación correcta sería que en la escala de Fa debe haber un semitono diatónico entre el LA y el SI, y por eso hay que escribir Si bemol, y punto, sin hablar de semitonos “cromáticos”. Pero claro, para un físico o un matemático, incluso para un informático, puntualizaciones como esta podrían resultar enrevesadas y hasta absurdas.

Creo que daremos en el clavo si enfocamos todo lo dicho con una sola pregunta: ¿Por qué debemos razonar todo en base a solamente 7 nombres de notas, cuando en realidad la cantidad de sonidos involucrados es mucho mayor?

Los músicos dirían que llevar las cosas hasta ese punto sería terriblemente complicado y puedo imaginar las objeciones a esta idea. Pero para quienes han seguido pacientemente el razonamiento matemático que hicimos en este artículo, ¿no es cierto que los sonidos podrían simplemente haberse numerado, 1,2,3,4… sin mencionar nota alguna, ni sostenidos ni bemoles, e igualmente habría quedado claro todo lo referente a intervalos y relaciones armónicas?

Para terminar entonces, no estoy proponiendo reformar la notación de la música, pero sí puedo concluir en que el concepto de “alteración” (sostenido y bemol) plantea un problema relacionado con la teoría de conjuntos. Es evidente que lo que en música se identifica como dos proyecciones de escalas en sentidos opuestos, una hacia los sostenidos y otra hacia los bemoles, donde hay sonidos coincidentes y otros no, se trata en realidad de la intersección de varios conjuntos:

Escala de Fa ∩ Escala de Do

Escala de Do ∩ Escala de Sol

Escala de Sol ∩ Escala de Re

Escala de Re ∩ Escala de La

Escala de La ∩ Escala de Mi

Escala de Mi ∩ Escala de Si

……………………………… teóricamente hasta el infinito, pues el conjunto no se agota en “la nota SI”, y ahí, precisamente ahí, los músicos ya dejan de entender cómo es posible seguir sin recurrir a las famosas “alteraciones”, el Fa# en este caso, para proseguir encadenando intervalos de “quinta” (3/2 en realidad).

Por una razón similar, es probable que un músico, luego de estudiar la posible escala temperada calculada sobre quintas que no están en proporción de 3/2 sino 2,996614 / 2, y que veíamos más arriba, observase rápidamente que entre los sonidos 10 y 11 se hallan las notas LA#-FA y objetase que eso no se trata de una “quinta” sino de una “sexta”, porque de LA a FA se cuentan 6 notas y no 5, y calificaría a ese intervalo como una “sexta disminuida enarmónica de la quinta justa”, (vaya, nada menos…) o que, en lugar de FA, habría que escribir MI#…pero, claro, comprendamos cómo es el caso: esto ocurre porque un músico pensará siempre según la escala de siete notas, la tradicional escala de 7 notas de toda la vida. Para un músico, si las notas son 6 es una “sexta”, pero, si mide un semitono menos, entonces la sexta es “disminuida”. Para evitar lo que los músicos entienden de sobra – pero que es una jerga que casi nadie más entiende – debemos introducir necesariamente el cálculo, donde todo intervalo resultante es “justo” y a nadie se le ocurre “aumentar” o “disminuir” el resultado.

Y esta puntualización nos lleva a afirmar que la nomenclatura normalmente aceptada para los intervalos entre notas no tiene el menor sentido.

Sin duda, se trata de una afirmación extraordinaria.

Y afirmaciones extraordinarias requieren pruebas extraordinarias: Como ya no tenemos siete notas (las generadas por las escalas de Aristógenes o Pitágoras), sino doce, separadas por intervalos iguales, habría que reconocer que lo que hemos llamado y todo el mundo llama “octava” debería llamarse en realidad “decimotercera”. ¿Cuántas notas se cuentan entre un DO y el siguiente DO, en este sistema? Si vamos de DO a DO se cuentan 13, ¿no? Y hay más: ¿cuántas notas hay entre cualquier nota y su “quinta justa”? Hay ocho, ¿no es cierto? Por lo tanto, lo que llamamos “quinta”, en el sistema temperado por igual, debería llamarse “octava”, y no “quinta”. ¿Es que acaso puede sorprender a alguien el hecho de que usamos una escala de 12 sonidos, incluso para la música tonal?

Seguro que a más de un músico le puede dar un infarto leyendo esto. Pero si nos fijamos ahora de nuevo en el cálculo de quintas sucesivas generadas para el temperamento igual, el que recién vimos, donde la “quinta” se calcula como 2,9966 / 2, ¿cuántas notas hay entre el LA# y el FA? Ése, que para un músico no es una quinta sino una sexta, es un intervalo que contiene 8 notas. Y es exactamente igual para todos los demás casos: entre DO y SOL, entre SI y FA#, entre FA y DO… todos los intervalos están separados por exactamente ocho notas y no hay excepción ninguna.

Pero… ¿no habíamos dicho que un bemol es diferente de un sostenido y que, aunque en el temperamento igual no hay diferencias, las puede haber, por ejemplo, para un violinista? Pues, por más discutible que todo este asunto pueda parecer, lo cierto es que el cálculo demuestra que para la afinación justa de cualquier intervalo siempre habrá una nota disponible en el conjunto de escalas en uso. Una vez determinado el intervalo, la cantidad de semitonos nunca varía, y la diferencia de una coma no es otra cosa que la afinación de acuerdo a los sonidos que el cálculo matemático pone a disposición. Cualquier músico puede hacer la prueba contando las notas que forman los semitonos: verá, para su tranquilidad, que ahí están los sostenidos o los bemoles – según sea la tonalidad donde el intervalo se sitúe. Lo que quizá le cueste entender es que algunas de las notas que cuenta pertenecen realmente a otras escalas y… aunque ya lo sepa, y diga que forman semitonos “cromáticos”, tal vez termine enredándose de nuevo al querer pensar de otra manera.

Lo que nos vuelve locos a todos, en fin, es la rémora del sistema “de toda la vida”: considerar que con tan sólo siete notas se puede explicar un sistema extraordinariamente complejo. Sin embargo, nada mejor que mirar bien los cálculos para ver dónde está el error de concepto cuando se razona solamente en base a notas. La dificultad es manifiesta si nos damos cuenta de que todos los elementos de los conjuntos que se intersectan no se pueden expresar con tan sólo 7 símbolos (los nombres de las notas).

Y hasta aquí este artículo dedicado a los filósofos griegos y su herencia.

En el próximo artículo veremos cómo la Edad Media sería el puente hacia la modernidad y cómo surgiría la invención de la escritura actual de la música, y por qué las notas llevan los nombres que tienen. Por cierto, el misticismo medieval no congeniaba nada con la ciencia, y ése sería un factor determinante para el futuro…