Hace unos días, en el último artículo, hablamos sobre las fuerzas centrales, pero lo hicimos todo cualitativamente. Como es costumbre en esta serie, vamos a rehacer lo que ya vimos en el último capítulo, pero para aquellos a los que no les asuste ver un poco de matemáticas.
Si no habéis leído el anterior capítulo id a leerlo, pues muchas de las cosas que hablé ahí son importantes para este artículo y no voy a repetir todas las cosas. Ahí discutimos la existencia de un vector, al que llamamos vector posición, que nos definía precisamente la posición de un objeto; y también hablamos sobre dos formas de escribir vectores, las coordenadas cartesianas y las polares. Un resumen muy general y rápido de las coordenadas cartesianas:
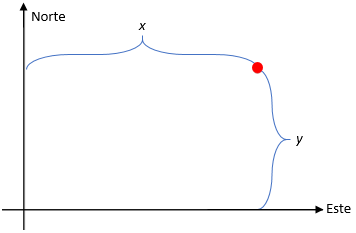
Un vector en dos dimensiones puede especificarse con dos números, especificando la distancia en dos direcciones perpendiculares. Por ejemplo, la distancia hacia el Este y la distancia hacia el Norte (que llamaremos, respectivamente x e y, siguiendo la nomenclatura típica).
Entonces cualquier punto se puede especificar con los números x e y. A estos dos números los llamaremos coordenadas cartesianas, y a partir de aquí ya podemos dejar de hablar de Este y Norte pues eran simplemente nombres para que todos pudiéramos entendernos. Vamos a renombrar la dirección Este por lo que llamaremos el Eje x y el Norte por el Eje y.
Además, podemos definir dos vectores unitarios (es decir, de módulo 1), x e y, considerando una persona moviéndose con y o x constante. El vector unitario x lo definimos como ese que señala la dirección donde la coordenada x aumenta en 1 unidad, permaneciendo la coordenada y constante. Y lo mismo para definir el vector unitario y. Imaginad ahora que fijamos un valor de y y dibujamos todos los puntos que obtenemos al ir cambiando x. Lo que observaríamos seria una recta horizontal, a una distancia y del origen. Por ejemplo, fijando y=1, debemos movernos una unidad hacia arriba, pero como no hemos fijado la posición x, podemos movernos hacia la izquierda o derecha, sin restricciones, generando la recta a la que antes me refería. Si en lugar de fijar y fijamos x, observaríamos una recta vertical. Si hacemos esto para muchos valores de x e y, obtenemos la siguiente imagen
En la imagen anterior pueden verse dos puntos (rojo y azul) sobre el plano cartesiano, además de las líneas que comentaba antes para los valores de x entre 0 y 8 (verticales) e y entre -1 y 6 (horizontales). Fijaos que las líneas correspondientes a x=0 e y=0 son precisamente los que definimos, respectivamente, como Eje y y Eje x. Esto nos permite saber rápidamente que el punto rojo está en las coordenadas (x=5, y=3) sin tener que calcular la distancia ni nada, pues está justo en la intersección de esas dos rectas.
En coordenadas cartesianas el vector posición r puede escribirse como
Ya que, como hemos dicho, el vector posición consiste en un vector que se mueve x unidades en la dirección x e y unidades en la dirección y.
Lo bueno de las coordenadas cartesianas es que, aunque otra persona se encuentre en un punto distinto al tuyo, todos estáis de acuerdo de hacia donde van los vectores unitarios x e y (es decir, x e y no dependen del punto en cuestión, esto puede apreciarse en la imagen anterior), por lo tanto, si un objeto se está moviendo desde una posición r1 a una posición r2 podemos definir la velocidad de ese objeto como
Donde usaré la notación de Newton y denotaré la derivada temporal con un punto sobre la cantidad a derivar. Del mismo modo podemos volver a derivar para obtener la aceleración del objeto
Si ahora queremos, por ejemplo, calcular la energía cinética del objeto, no tenemos más que calcularla con la ecuación que ya conocemos
Y así podemos ir calculando todo lo demás.
Vamos ahora a ver qué diferencias aparecen al considerar las coordenadas polares:
En el artículo anterior vimos que las coordenadas polares consisten en describir el vector r con la distancia al origen y el ángulo que forma con el eje x.
Si repetimos lo mismo que hemos hecho para coordenadas cartesianas y fijamos un valor de r, dibujando todos los puntos que obtenemos al variar θ ¿qué figura obtenemos? ¡Pues los puntos que están a una misma distancia del origen forman una circunferencia de radio r y centrada en el origen! Si en cambio fijamos θ y movemos r obtenemos rectas que salen del origen y forman un ángulo θ respecto al eje x. Dibujemos estas figuras para varios valores de r y θ:
De nuevo, definimos los vectores unitarios r y θ como dos vectores de módulo 1 y con la dirección y sentido en que aumenta r o θ, manteniendo el otro valor constante. Pero observemos ahora una gran diferencia con las coordenadas cartesianas: para dos observadores, uno en el punto rojo y el otro en el punto azul, los vectores x e y son exactamente los mismos, ¡pero los vectores r y θ no! Esta diferencia es fundamental y, como podréis imaginar, en general sólo complica aún más las cosas, pero si estamos viendo esto es porque hay veces en los que esta aparente complicación permite simplificar las cosas. Por ejemplo, el vector posición se escribe mucho más fácilmente con estas coordenadas
Pues precisamente esta es la definición del vector unitario r.[1] En dos dimensiones, cuando encontramos dos vectores con los que podemos generar cualquier vector (es decir, que cualquier vector se puede escribir como suma de esos dos vectores) decimos que estos vectores forman una base. Por ejemplo, los vectores unitarios que hemos viso, x e y son una base y los vectores unitarios r y θ también. La primera es una base de coordenadas cartesianas, mientras que la segunda es una base de coordenadas polares. Existe otra base muy usada en coordenadas polares, con los vectores er y eθ siguientes:
La base de r y θ es útil porque ambos vectores son ortogonales y tienen modulo 1, a eso se le llama base ortonormal; er y eθ no es una base ortonormal, pero tiene otras propiedades interesantes (que no vamos a ver aquí).
Como hemos dicho que x e y forman una base, cualquier vector del plano se puede escribir como combinación de los vectores x e y. Entonces los vectores r y θ no pueden ser una excepción a eso. Con un poco de trigonometría es fácil ver que podemos relacionar las dos bases con
Vemos que evidentemente los vectores r y θ dependen de la coordenada θ.
Esta dependencia hace que, si una persona se mueve por el espacio, los vectores r y θ irán cambiando; para ver cómo cambian podemos simplemente calcular su derivada, pues es lo que nos indica cómo cambian las cosas.[2] Lo primero que podemos notar es que ni r ni θ dependen de la coordenada r, así que si nos movemos siguiendo la coordenada r ambos vectores permanecen iguales. Pero si nos movemos modificando el valor de θ observamos que los vectores cambian de la siguiente forma:
En un artículo anterior hablé sobre la regla del producto de derivadas. Para continuar necesito comentar una última regla muy útil para derivar, la conocida como regla de la cadena. Suponed que tenemos una función f que depende de dos variables, por ejemplo r y θ. Suponed además que tenemos un objeto moviéndose por el espacio y, por tanto, las coordenadas r y θ van cambiando con el tiempo ¿cómo podemos calcular el cambio que sufre f?
Dado que f es una función que depende de las variables r y θ, podemos derivar respecto a esas variables para conocer cómo de “sensible” es nuestra función a los cambios de esas variables. Pero eso no es suficiente, no sólo debemos conocer lo sensible que es la función a los cambios de r y θ, debemos tener en cuenta cuánto cambian r y θ por el hecho de que el objeto se mueve. Pues por mucho que cambie f al cambiar r, si r cambia muy poco f cambiará muy poco, mientras que si f cambia poco al cambiar θ, si θ cambia mucho el cambio de f puede hacerse muy grande.
Si juntamos estos dos efectos podemos calcular el cambio de f de la siguiente forma
Donde he usado el símbolo de derivada parcial: simplemente, como f depende de dos variables, r y θ, la derivada parcial respecto de r nos dice que derivemos f respecto de r como siempre hemos hecho considerando que θ es un numero constante. Nuestro colega jlese ya habló de ella en este artículo, así que no voy a hablar más sobre esto.
Como veis, trabajar con coordenadas polares lleva un poco más de trabajo, pero una vez hemos hecho todo esto podemos llegar a resultados muy útiles. Recordando cómo se escribe el vector posición y usando todas las técnicas de derivar que conocemos podemos calcular los vectores velocidad y aceleración.
Y con esto podemos calcular la energía cinética de un objeto en movimiento
Ha sido un largo camino hasta llegar hasta aquí, pero al fin podemos ver por qué son útiles las coordenadas polares ¿Recordáis el anterior artículo donde hablamos de lo que eran las fuerzas centrales? Ahí dijimos que eran fuerzas que cumplían que:
- Su dirección siempre era radial, es decir, la misma dirección (y sentido) que el vector posición.
- Su módulo sólo depende de la distancia al origen, es decir, la coordenada r.
En resumen, una fuerza central en coordenadas polares se puede escribir como
Aplicando la segunda ley de Newton (que vimos en el artículo sobre la conservación del momento), podemos escribir (con la ecuación para la aceleración que ya hemos visto)
Multiplicando la segunda ecuación por r obtenemos un resultado muy interesante
En la última expresión he usado la regla del producto de derivadas que vimos el otro día,[3] el resultado que obtenemos es muy interesante, pues hemos visto que la derivada de una cantidad respecto al tiempo es cero, es decir, que esta cantidad no cambia con el tiempo (recordad que las derivadas nos indican cómo cambian las cosas). Entonces, la cantidad entre paréntesis debe ser constante… ¿alguien tiene idea de qué significado físico puede tener eso?
¡Pues resulta que ese producto es justamente el momento angular! Recordad que el módulo del producto vectorial de dos vectores se podía escribir como
O escribiéndolo de otra forma
Recordad que L es simplemente una constante, por lo que hemos encontrado una relación entre la derivada temporal de θ y r, es decir, no son magnitudes independientes: si conocemos una podemos conocer la otra. En un artículo anterior definí la energía potencial debido a una fuerza como
Usando la elección arbitraria de que la energía potencial valga cero cuando r se va a infinito. Lo importante de esta ecuación es simplemente que podemos definir la energía potencial; para cada función f esta energía será diferente. No nos interesa calcularla por ahora, solamente saber que existe y se puede calcular. Juntemos ahora todo lo que hemos visto para escribir la fórmula de la conservación de la energía
Fijaos que no hay dependencia de θ, hemos encontrado que la energía depende únicamente de la coordenada r y su derivada. Además fijaos en cómo se escribe la conservación de la energía para un problema unidimensional:
Comparando ambas expresiones podemos definir una función que llamamos el potencial efectivo como
Entonces ¡hemos simplificado un problema de varias dimensiones a un problema equivalente en una sola dimensión! Este potencial efectivo es el que dibujamos en las gráficas del anterior artículo. No voy a extenderme mucho más pues ya le he dedicado dos artículos.
Hasta aquí este artículo. En el siguiente vamos a ver en detalle el caso de una fuerza central proporcional a r-2 ¡Y con eso ya nos acercamos a los conocimientos necesarios para entender el modelo de Rutherford! Hasta pronto.
- Puede parecer que el vector posición depende solamente de la coordenada r, es un error común, recordad que r depende del ángulo θ. [↩]
- La velocidad, por ejemplo, nos dice cómo cambia la posición con el tiempo, etc… [↩]
- Pero en lugar de expresar el producto de una derivada como cosas más sencillas he hecho justo lo contrario. [↩]

The [De Thomson a Bohr, historia de un átomo] 0-Conceptos previos 9: Fuerzas Centrales (Parte II) by Roger Balsach, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.















{ 3 } Comentarios
¿Qué significa r con un puntito o dos puntitos encima?
Un puntito encima es la notación que se emplea para abreviar “primera derivada de r con relación al tiempo”, la velocidad de variación de r. Dos puntitos es la segunda derivada.
Excelente artículo!! Felicitaciones. Habrá más?
Escribe un comentario