En el larguísimo artículo anterior de esta tan presuntuosa serie sobre Lógica, para la que estoy usando extensivamente los amarillentos apuntes de la asignatura de “Metodología” de Segundo de Carrera, año académico 1973-74, impartida por Don José Cuena Bartolomé, vimos qué son las implicaciones lógicas, y sobre todo cuál es su fórmula, cómo se traducen en cálculo proposicional y cómo pueden evaluarse.
Llegamos a que  , o sea, la implicación es cierta si el antecedente es falso o verdadero el consecuente (o ambas cosas, claro), e intenté justificar por qué es así y no de otra manera. Espero haberlo conseguido.
, o sea, la implicación es cierta si el antecedente es falso o verdadero el consecuente (o ambas cosas, claro), e intenté justificar por qué es así y no de otra manera. Espero haberlo conseguido.
Esto, en álgebra de Boole, se representa así:  .
.
Estamos más o menos en marzo de 1974. Semana Santa acecha, con sus consabidas vacaciones y sus exámenes parciales, se acercan los exámenes finales, y hay que apretar. Veamos cómo empieza hoy la clase Pepe Cuena…
Pero antes de comenzar a deducir nada debo insistir una vez más en cuál es la función de la Lógica formal que estoy contando, con la inestimable ayuda de Pepe Cuena a través del Túnel del Tiempo.
Hemos visto que, teniendo de unas ciertas proposiciones individuales, éstas se pueden combinar de mil y una formas, mediante disyuntivas, conjuntivas o negaciones, con implicaciones, etc, mediante el cálculo proposicional. En todos los casos hemos visto cómo calcular el valor de verdad de la proposición compuesta resultante en base a los valores de verdad de las proposiciones atómicas que las componen, bien de forma algebraica, bien mediante las tan útiles tablas de verdad. Hemos puesto diversos ejemplos, rebatido falacias… y hay que reconocer que el resultado de alguna de estas frases era, cuando menos, chocante, sobre todo cuando lidiábamos con las consecuencias de la escurridiza implicación lógica del capítulo anterior.
Por ejemplo, una frase como “Si la arcilla es un metal, entonces es maleable” es radicalmente verdadera, por mucho que todos sepamos que la arcilla no es de ninguna manera un metal. Y es así porque sólo resultaría falsa en el caso de que siendo verdadero el antecedente (La arcilla es un metal) entonces fuera falso el consecuente (la arcilla es maleable). Como resulta que la arcilla sí es maleable, ese caso no se da, y por tanto la implicación es verdadera. Y eso nos choca, nos suena a cuento chino y nos hace desconfiar de los resultados de la aplicación de las fórmulas… ¡Si ya decía yo que la implicación era escurridiza!
Entonces ¿qué es lo que ocurre? Pues dos cositas, dos nimios detalles que muchas veces damos por sentado y otras… olvidamos, a saber:
Primero: La Lógica trata con proposiciones, y dije en el capítulo correspondiente, he repetido varias veces desde entonces y repito una vez más ahora que “Una proposición es una frase a la que podemos atribuir sin ningún género de duda un valor de certeza o falsedad”. Atención: “sin ningún género de duda”.
Esto elimina todas las frases que no sean objetivamente catalogables en cierto momento como verdad o mentira, es decir, muchísimas afirmaciones de filósofos y pensadores de todos los tiempos que tienen que ver con la divinidad, la naturaleza humana, la moral, etc, etc. Por ejemplo, la frase “Los arios son una raza superior” seguramente sería clasificada como verdad inmutable por los jerarcas y pensadores nazis, pero sería terminantemente catalogada como falsa de toda falsedad por casi todos los demás. ¿Es verdadera o es falsa? ¿Qué conclusiones podemos obtener de cualquier proposición compleja en la que aparezca esta frasecita? Pues eso.
Y segundo, y casi más importante: La Lógica formal no entiende nada acerca de si una proposición individual es verdadera o falsa. No tiene ni la menor idea de si p o q son verdaderas o falsas, ni le importa, ni le interesa lo más mínimo. Lo que sí formaliza es qué les ocurre a las diferentes proposiciones complejas que se forman conjugando o negando o implicando proposiciones individuales, en función de los diferentes valores de verdad de las proposiciones individuales que las forman.
Asegura la Lógica que, por ejemplo, si tenemos la proposición (p•q), esa proposición compleja sólo será cierta si tanto p como q son ciertas, y en cualquier otro caso, p•q es falsa. ¿Qué es lo que dice esta aseveración acerca del valor de verdad o falsedad de p y de q?
Efectivamente: Nada. Nada de nada.
Entonces, ¿quién es el responsable de fijar en cada caso si p o q son verdaderas o falsas? Nosotros, desde luego. No “La Lógica”, sino nuestra percepción o nuestro conocimiento o nuestras costumbres o lo que sea. Para fijar qué proposiciones son ciertas y cuáles falsas están otras disciplinas filosóficas (Ética, Moral, Ontología, etc), o científicas (Termodinámica, Trigonometría, Floricultura, Cromodinámica cuántica, etc). No la Lógica.
En este aspecto la Lógica es como la Matemática: ésta última permite transformar ecuaciones en base a una serie de reglas (por ejemplo, los axiomas de Peano) sin entrar a descifrar su significado. Son otras ramas de la ciencia quienes “descifran” las ecuaciones y las aplican a casos concretos del mundo real; por ejemplo, la fórmula V=I•R (la famosa Ley de Ohm) sale como consecuencia de la aplicación estricta de las reglas matemáticas sobre una serie de otras ecuaciones iniciales. Quien decide si las ecuaciones de partida son verdaderas o falsas no es la Matemática, claro, sino los físicos de la Electricidad. La Matemática garantiza nada más (¡y nada menos!) que todas las transformaciones matemáticas realizadas hasta llegar a V=I•R son correctas, así que si las ecuaciones iniciales son verdaderas, entonces la conclusión lo es también. Fijaos bien: si las ecuaciones iniciales son verdaderas.
Pues lo mismo ocurre con la Lógica. Dadas una serie de proposiciones iniciales combinadas de cierta manera, por complicada que ésta sea, la Lógica (que no deja de ser una rama de la Matemática) nos dice cómo podemos transformarlas y nos asegura qué les ocurre a las proposiciones que con ellas se forman, según sea el valor de verdad o falsedad de esas proposiciones iniciales… valor de certeza o falsedad que tienen que proporcionar otras personas u otras ciencias. No la Lógica.
Espero haber aclarado un poco más este concepto, que será muy importante para ver lo que viene a continuación: cómo se razona formalmente usando las reglas de la Lógica, es decir, cómo se pueden deducir unas cosas a partir de otras mediante la aplicación razonada de todos los artefactos lógicos que hemos visto hasta ahora. Es decir, vamos a usar los ladrillitos que hemos ido fabricando en los capítulos anteriores para construir primero paredes, luego edificios, luego ciudades… En una palabra, vamos ya a destripar el proceso de Deducción Lógica.
.
Antes que nada, hay que definir formalmente qué es una Tautología, puesto que nos hará falta manejar bien este concepto en todo lo que sigue.
Una Tautología es una proposición lógica que es siempre verdad, pero siempre, siempre, como las promesas de un político, cualesquiera sean los valores de verdad de las proposiciones atómicas que la componen. Por ejemplo, la estúpida frase “Hace calor O No hace calor”, es una tautología: tanto da si hace calor como si no, por fas o por nefas, la frase resultante es obviamente cierta. Muchos políticos, analistas, consultores, economistas y demás basan sus discursos en tautologías más o menos elaboradas para que no resulten tan evidentes a primera vista, de tal modo que sea poco menos que imposible que se equivoquen en sus predicciones. Y aún así, no consiguen acertar…
El caso contrario, cuando una proposición lógica es intrínsecamente falsa, independientemente de los valores de verdad de las proposiciones atómicas individuales que la forman, se llama Contradicción. “Llueve Y no llueve” es una contradicción: pase lo que pase en la calle, es falsa. Frase idiota,[1] y encima falsa.
.
Definidos estos dos conceptos, para seguir con la exposición hay que definir matemáticamente cómo es la deducción.
Según la Real Academia de la Lengua, deducir es “Inferir, sacar consecuencias de un principio, proposición o supuesto“. No es ésta una definición matemática, como podréis comprobar, así que habrá que ponerse a ello…
Desde ese punto de vista formal, la deducción, que es una de las herramientas matemáticas y lógicas más potentes, consiste en deducir (inferir, construir, crear) nuevas frases a partir de otras preexistentes, llamadas premisas, de tal modo que, si las premisas son todas ellas ciertas, también lo sea la frase deducida, la conclusión.
Esto es intuitivo, de acuerdo, pero hay que asegurarse bien de que cuando deducimos algo, estamos haciéndolo bien, es decir, tenemos que asegurar formalmente que el proceso de deducción en sí mismo es correcto.
En una palabra, si las premisas en que nos basamos, los antecedentes, son verdaderos, entonces, de forma irremediable, obligatoria, necesaria, el consecuente, lo deducido, debe ser verdadero también. Si no fuera así es que el propio proceso deductivo es erróneo.
.
En realidad, estamos tan acostumbrados a deducir cosas a partir de otras, a inferir resultados, comportamientos y acciones a partir de otros, que damos el proceso por sentado. Y no es así.
Bueno, no es que no sea así, entendedme, pero hay que formalizarlo para que podamos decir sin temor a equivocarnos que cuando deducimos unas cosas a partir de otras lo hacemos bien, es decir: que podemos fiarnos del resultado de la deducción, para poder seguir deduciendo otras frases a partir de ahí.
Es la base, esto es la base de prácticamente todo en la ciencia y la matemática. Si esto no funciona… se nos cae todo el edificio matemático, así que mejor formalizarlo, y hacerlo bien.
.
Veamos:
Si tenemos, por ejemplo, tres premisas A, B y C,[2] y queremos deducir de ellas una conclusión D, debe ocurrir que cuando todas las premisas son verdad (es decir, en cálculo proposicional:  ), entonces la conclusión (D) debe ser también verdad, es decir, igual a 1, o sea,
), entonces la conclusión (D) debe ser también verdad, es decir, igual a 1, o sea,  .
.
Para expresar esta frase según los dictados de la Lógica formal necesitamos de una buena implicación, que para eso las conocemos ya y no nos asustan.
La fórmula es, evidentemente: 
Fórmula que en español leeríamos, más o menos: “Si ocurren simultáneamente A, B y C, entonces ocurre D, y esto pasa siempre, siempre“.
.
¿Cómo se interpreta esta formulita de arriba?[3]
Pues que siempre que se cumple que las tres premisas son ciertas,[4] la conclusión debe serlo también, por lo que la propia implicación lógica debe ser también verdad… o sea, una tautología.[5]
En una palabra, la tabla de verdad de la expresión anterior, ![[A \wedge B \wedge C \Longrightarrow D = 1]](https://eltamiz.com/elcedazo/wp-content/cache/tex_c8eaac9eb3c1b14b3d7dba437ec053d6.png) debe ser una tautología, es decir, todos los valores resultado para todas las combinaciones posibles de valores deben ser 1. Si no fuera una tautología, si con alguna cierta combinación de valores de A, B y C, por un lado, y de D, por el otro, la implicación diera un resultado falso, no podríamos deducir nada, no sería una deducción válida, o mejor dicho, se trataría de una deducción no válida, incorrecta.
debe ser una tautología, es decir, todos los valores resultado para todas las combinaciones posibles de valores deben ser 1. Si no fuera una tautología, si con alguna cierta combinación de valores de A, B y C, por un lado, y de D, por el otro, la implicación diera un resultado falso, no podríamos deducir nada, no sería una deducción válida, o mejor dicho, se trataría de una deducción no válida, incorrecta.
Ahora bien, si recordáis la tabla de verdad de la implicación lógica,  (en nuestro ejemplo p es la conjunción de las tres premisas originales:
(en nuestro ejemplo p es la conjunción de las tres premisas originales:  ), hay un caso en que el resultado de la implicación es falso… ¿Recordáis? Sí, seguro que recordáis:
), hay un caso en que el resultado de la implicación es falso… ¿Recordáis? Sí, seguro que recordáis:
|
p |
q |
|
|
V |
V |
V |
|
V |
F |
F |
|
F |
V |
V |
|
F |
F |
V |
Esto choca con lo que acabo de decir, que para que la deducción sea posible es preciso que  , y esto para cualquier valor, luego debe ser obligatoriamente una tautología… O sea, que hay que quitarse de enmedio esa fatídica “F“.[6]
, y esto para cualquier valor, luego debe ser obligatoriamente una tautología… O sea, que hay que quitarse de enmedio esa fatídica “F“.[6]
¿Cómo resolverlo? No queda más remedio que obligar a que, cuando p sea verdad, q sea obligatoriamente verdad. Y hay que darle una forma formal, valga la redundancia.
.
Desde hace muchos cientos de años los filósofos se han ocupado de este problema, que no es ni más ni menos que la forma común de razonar de la gente, pero, además, es un razonamiento central a la matemática y la ciencia en sí. En el lenguaje corriente se ha llegado a una fórmula que representa fielmente esta forma de razonar, de deducir cosas a partir de otras con la seguridad de que el razonamiento es correcto. Esta fórmula tiene desde tiempos antiguos un llamativo nombre en latín que a muchos os sonará: modus ponens (o, para los más precisos, “modus ponendo ponens”, toma ya).
El modus ponens se representa de la forma siguiente:



.
Que las fórmulas no nos acobarden: es muy sencillo, en realidad, e intuitivo. Veámoslo con un ejemplo que ya hemos analizado hasta la saciedad en el artículo anterior, con estornudos y ojos que se cierran:
Estoy estornudando.
Si estornudo, cierro los ojos.
Luego: Cierro los ojos.
El sentido común nos dice que esto es efectivamente así, que el razonamiento es plenamente correcto: si es cierto que “estoy estornudando“, y es también cierto que “si estornudo, entonces cierro los ojos“, si ambas son ciertas, repito, y sólo en ese caso,[7] entonces indefectiblemente debo estar con los ojos cerrados. Ciego total. Sin ver ni un pimiento.
Y en el ejemplo del prometedor (porque promete cosas) político del último artículo, ése que decía que “Si gano la elección construiré un hospital“, imaginemos que le hemos creído a pies juntillas, que le votamos y que al final ganó la elección. Por tanto, podríamos asegurar que:
El político ganó la elección.
Si gana la elección, entonces construirá un hospital.
Ergo: Construirá un hospital. Esta conclusión es indefectible, inevitable como el devenir de las estaciones: en unos meses o un par de años habrá un nuevo hospital en la zona…
…Ah. ¿Que no lo construyeron? Vaya. Qué cosas.
Pues el razonamiento está bien hecho, es un razonamiento correcto, ni Descartes lo hubiera hecho mejor… así que en este caso habrá que reexaminar la certeza o falsedad de las premisas. Como parece innegable que nuestro político ganó la elección, que yo le he visto celebrarlo efusivamente en la tele, parece que la única posibilidad factible para que no tengamos hospital nuevo es que la frase “Si gano la elección, construiré un hospital” sea falsa. Falsa como un billete de 38 euros y medio…
Entonces, si la frase de marras, la promesa electoral de nuestro amigo, es falsa, simple y llanamente falsa, es porque, vean Vds., quien la dijo, mintió. Ni más ni menos. Nos la ha dado con queso, nos ha engañado, nos ha hecho un trile. Así que, en justa correspondencia, escarmentados, en las próximas elecciones no le votamos más, por mentiroso.
Ah, ¿que esto tampoco es exactamente así…? Uff, ya decía yo que de Lógica humana sabía yo más bien poco…
.
Sigamos con el razonamiento. El modus ponens se especificaba como:



Bien. Si escribimos todo esto según los dictados del cálculo proposicional, llegaremos a que ![[p \wedge (p \Longrightarrow q) \Longrightarrow q] = 1](https://eltamiz.com/elcedazo/wp-content/cache/tex_3e4cbae472a6831b329a1c58435a9737.png) .
.
Efectivamente, la conjunción (Y) de las dos premisas implicando la conclusión es una tautología. El que una de las dos premisas sea otra implicación es, en realidad, irrelevante, pues no deja de ser una proposición, ni más ni menos que una proposición monda y lironda como otra cualquiera, que puede ser evaluada como cierta o falsa sin dificultad.
Supongo, además, que os habéis dado cuenta de que para obtener un modus ponens con toda la barba, y a la luz del Cálculo Proposicional y su propiedad conmutativa, el orden en que se presentan las dos premisas es irrelevante. Es decir, también sería un modus ponens válido si expresamos las proposiciones de la forma siguiente:[8]



.
Sólo queda comprobar una pequeña cosita… ¿en verdad esta construcción es una tautología?
No os fiéis de mi palabra: comprobémoslo, como siempre, mirando su tabla de verdad.
|
p |
q |
es decir:
|
|
es decir:
|
|
V |
V |
V |
V |
V |
|
V |
F |
F |
F |
V |
|
F |
V |
V |
F |
V |
|
F |
F |
V |
F |
V |
Efectivamente, resulta una tautología, su resultado siempre es verdadero. ¿No lo ves? Espera, vamos a hacerlo mediante nuestra amiga, la eficacísima álgebra de Boole, verás qué rápido lo entiendes.
![[p \wedge (p \Longrightarrow q)] \Longrightarrow q =](https://eltamiz.com/elcedazo/wp-content/cache/tex_4551c2d1a1ad3abcb56e05042fd39d76.png)
![[p (p \Longrightarrow q)] \Longrightarrow q =](https://eltamiz.com/elcedazo/wp-content/cache/tex_1fe44d4a1182f7d0becec79c698fd2bf.png)
![[p(p'+q)] \Longrightarrow q =](https://eltamiz.com/elcedazo/wp-content/cache/tex_4b5575ca4a6cf64a921f7903e52bb770.png)
![[pp'+pq)] \Longrightarrow q =](https://eltamiz.com/elcedazo/wp-content/cache/tex_46291f1bf4c9047d38ae66fbdf1e5092.png)
![[0+pq)] \Longrightarrow q =](https://eltamiz.com/elcedazo/wp-content/cache/tex_0c37a743bbb8a9e2bedd3a258b7f6f6a.png)





Listo.[9]
Por lo tanto, el hecho de deducir es ver si puede existir formalmente una relación tal que, cuando la conjunción de todas las premisas sea verdad (o sea, todas ellas son simultáneamente verdad) entonces la conclusión ha de ser necesariamente verdad.
Si alguna de las premisas es falsa entonces la conclusión puede ser verdadera, falsa o mediopensionista, no podremos asegurar nada en absoluto sobre ella, como ocurre en el ejemplo de la hospitalaria promesa del político.
Por cierto, y esto es importante, el razonamiento puede ser correcto o incorrecto, nunca verdadero o falso. Las premisas lo son, verdaderas o falsas; el razonamiento en sí no lo es. Si el razonamiento que hemos hecho es correcto, entonces, cuando todas las premisas sean verdad, y sólo en ese caso, podemos asegurar que la conclusión es verdadera también. Eso es lo que se llama una buena deducción…
.
Atención: Podría parecer que el proceso deductivo sólo puede hacerse con Leyes Universales, con enunciados que abarquen a todo un conjunto universal, incluso a todo un Universo… Pues no, señores, no es así. El proceso descrito hasta ahora es correcto sean como sean los enunciados sobre los que se aplica… siempre que las premisas sean ciertas, insisto por enésima vez.
Tanto da que apliquemos el proceso deductivo a la Ley de la Relatividad General[10], como al hecho de si como o no como palomitas en el cine.[11] En ambos casos el proceso de falsamiento es el mismo: buscar contraejemplos.[12] Claro que las repercusiones de falsar la Relatividad General no son comparables a las de falsar mi impenitente avidez por palomitas en el cine… pero el proceso en sí es idéntico. Idéntico.
.
Pongamos un ejemplito de proceso deductivo. Chiquitín.[13] Ver si lo siguiente es un razonamiento correcto… o no. El ejemplo es el siguiente:



.
¿Entendéis algo? ¿No? Vaaaaale, pongámosle nombre a las proposiciones:
a: Soy español.
b: Tengo bigote.
c: Me gusta el futbol.
d: Me gustan los toros.
Con estas premisas, el razonamiento a comprobar es el siguiente:
Premisas:
“Si soy español y tengo bigote, entonces me gustan el fútbol y los toros.“
“O no tengo bigote o no me gustan los toros (o ambas cosas, como siempre)“.
Y la conclusión sería: “O no soy español o no tengo bigote“.
¿Se ve mejor así…? Se trata de comprobar si éste es un razonamiento correcto, si se puede deducir la conclusión de esas dos premisas.
.
Vamos con ello. Hay dos premisas,  , por un lado, y por el otro
, por un lado, y por el otro  .
.
Si ambas son ciertas, entonces la conclusión,  , debe serlo también. Es decir,
, debe serlo también. Es decir, ![[(a\wedge b \Longrightarrow c\wedge d) \wedge (\neg b \vee \neg d) \Longrightarrow \neg a \vee \neg b] = 1](https://eltamiz.com/elcedazo/wp-content/cache/tex_d703c41e2c4c4210e522db3bfa582a92.png)
Para comprobarlo, construyamos la fórmula de la deducción en álgebra de Boole y, simplificando, veamos si es efectivamente su valor es 1 en toda ocasión. Esa fórmula es:
![[(ab \Longrightarrow cd)(b'+d')] \Longrightarrow (a'+b')](https://eltamiz.com/elcedazo/wp-content/cache/tex_68a165d18e672d1e8d0c4d9b9d8cca41.png) , que es lo mismo que:
, que es lo mismo que:
![[((ab)'+cd)(b'+d')]'+(a'+b') =](https://eltamiz.com/elcedazo/wp-content/cache/tex_4948619f480b4e2567e3cc21c246adb8.png) Aplicando las Leyes de De Morgan:
Aplicando las Leyes de De Morgan:
![[(a'+b'+cd)(b'+d')]'+a'+b' =](https://eltamiz.com/elcedazo/wp-content/cache/tex_dbc1b4c76a07bcdf28d8746062f02785.png)


 Reordenando:
Reordenando:
 Aplicando la distributiva del + sobre el · (ésa que tan rara se nos hace):
Aplicando la distributiva del + sobre el · (ésa que tan rara se nos hace):
 Y aplicando nuevamente la distributiva del + sobre el · :
Y aplicando nuevamente la distributiva del + sobre el · :



 Reordenando de nuevo:
Reordenando de nuevo:
 Y otra vez la distributiva del + sobre el · :
Y otra vez la distributiva del + sobre el · :



Bufff. Efectivamente, la tabla de verdad del razonamiento es una tautología. O sea, que, sólo en el caso de que las dos premisas sean verdaderas, o no soy español o no tengo bigote (o ambas cosas, recordemos que el O no es exclusivo). El razonamiento está bien hecho, pues. Es correcto. Pero, no nos olvidemos, insisto, sólo podemos asegurar que la conclusión  es cierta cuando ambas premisas,
es cierta cuando ambas premisas,  y
y  sean ciertas. Si alguna no lo es… vaya Vd. a saber lo que le pasará a la conclusión, podría ser cierta o falsa, nada podemos decir de ella.
sean ciertas. Si alguna no lo es… vaya Vd. a saber lo que le pasará a la conclusión, podría ser cierta o falsa, nada podemos decir de ella.
.
A continuación, una serie de razonamientos correctos. Muchos de ellos completamente obvios, además. Dejo al lector la tarea de demostrarlo (advierto: son muchísimo más sencillos que el ejemplo anterior). Para hacerlo, recordad, bastará demostrar que la conjunción de las premisas (o la única premisa, si es que sólo hay una) implicando la conclusión es una tautología:[14]
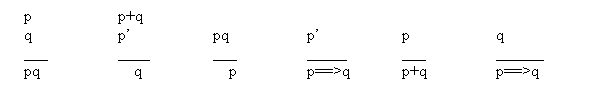
Etc. Aconsejo echarle una miradita a estos razonamientos correctos. Alguno de ellos seguramente os parecerá sorprendente, por ejemplo el último… pero a poco que lo penséis (¡o lo calculéis!) os daréis cuenta que todos son correctos y obvios.
.
Naturalmente, en la vida real no siempre se conoce de antemano la conclusión. Es posible que un científico[15] suponga que ocurre algo (la conclusión buscada) y realice el razonamiento deductivo correspondiente para asegurarse de que la conclusión puede derivarse de las premisas conocidas. Pero es más común, creo yo, tener una serie de premisas que son (o se suponen) ciertas y, a partir de ellas, elaborar el razonamiento deductivo hasta llegar a una conclusión. Si el razonamiento está bien hecho, si no es falaz, la conclusión debe ser cierta también (si y sólo si las premisas son ciertas, lo repito una vez más).
.
Veamos ahora el razonamiento que hizo el nene luthierano al que su mamá amenazaba con el Hombre de la Bolsa si no tomaba la sopa que vimos en el último ejemplo del artículo anterior. Le decía su mamá: “Si no tomás la sopa, viene el Hombre de la Bolsa“. Y el nene, a pesar de la amenaza, no se tomó la sopa, que no le gustaba ni un poquito. Entonces, el nene se planteó el siguiente modus ponens:[16]



El nene esperó, aterrado, a que el Hombre de la Bolsa viniera a hacer lo que sea que se supone que haga ese siniestro individuo. Pero, pasado un rato prudencial, El Hombre de la Bolsa no vino. La conclusión del razonamiento era, definitivamente, falsa.
¿Qué conclusión, valga la redundancia, sacó el nene de todo esto? Pues que hay algo mal en el planteamiento anterior. O el razonamiento está mal hecho, o alguna de las premisas era falsa (o las dos a la vez).
El nene rápidamente se da cuenta de que el razonamiento es impecable: ¡Si es un modus ponens que ni el mismísimo Aristóteles lo hubiera mejorado! Luego entonces deben ser las premisas; alguna de ellas es falsa, no hay duda. Tan sólo mirando el plato lleno de sopa, y el vacío en su estómago, ya se da cuenta de que la proposición “El nene no tomó la sopa” es cierta, está clarísimo. Luego, por eliminación, es la otra premisa la que está mal, la que es falsa…
Vaya. Entonces, no es cierto que “Si no me tomo la sopa, Viene el Hombre de la Bolsa“. Amenazante frase pronunciada por su mamá, que ha quedado retratada como una… mentirosa. Amante, sí, pero mentirosa. El nene aprendió que no todas las cosas que dicen los adultos, ni siquiera su mamá, son ciertas… ¡Ya se está preparando para la vida adulta!
De todos modos, como los mismos Les Luthiers concluyen al respecto, “Señora… ¿A quién se le ocurre amenazar con un folklórico personaje imaginario…? Puestos en el caso es mucho mejor amenazar con horrores más tangibles: El lobo, la araña, una buena víbora…“. Grandes, Les Luthiers. MUY grandes.
.
Volviendo a lo que nos ocupa, es sencillo ver que si el razonamiento es cierto para dos premisas y una conclusión será también válido para tres premisas (pues basta con considerar que una de las premisas es la conjunción de las otras dos).
No hay que ser muy listo, entonces, para darse cuenta de que sirve igual para un número cualquiera de premisas  . En este caso, podemos decir que
. En este caso, podemos decir que ![[P_1 \cdot P_2 \cdot \cdot P_n\Longrightarrow q]= 1](https://eltamiz.com/elcedazo/wp-content/cache/tex_eb017f5cdeb9a38abfdfc4b794dbf079.png) . No me voy a detener en la demostración, porque es muy sencilla e intuitiva y, queridos lectores, tenéis herramientas más que suficientes para poder demostrarlo fácilmente. Y pasar un buen rato. Supongo.
. No me voy a detener en la demostración, porque es muy sencilla e intuitiva y, queridos lectores, tenéis herramientas más que suficientes para poder demostrarlo fácilmente. Y pasar un buen rato. Supongo.
.
Igual alguno de vosotros está pensando “Yo estudié alguna vez no sólo el modus ponens, sino también el modus tollens y no sé cuántos modus más… y no los veo por parte alguna”. Tenéis razón. Ni los veis ni los vais a ver: no hacen ninguna falta. Sabiendo cálculo proposicional y cómo es el modus ponens, todos los demás modus aparecen naturalmente de él.
Veamos, por ejemplo, el “modus tollendo tollens“, más conocido por modus tollens a secas, y que tan importante es para el Falsacionismo. Dice el modus tollens:



O sea, si se cumple que A implica a B, y se cumple la negación de B, entonces la conclusión es la negación de A. ¿En qué se diferencia esto de un modus ponens? En poco: que las proposiciones A y B están negadas y sin negar en diferentes sitios… ¿y eso nos asusta?
Fijaos bien, para saber si esta forma de razonar llamada modus tolllens es correcta, hay que hacer exactamente lo mismo que hicimos con el modus ponens: descubrir si la conjunción de las premisas implicando la conclusión es una tautología.
O sea, ![[(A \Longrightarrow B) \wedge \neg B] \Longrightarrow \neg A](https://eltamiz.com/elcedazo/wp-content/cache/tex_64121fb03d92ed7782e228a97b751454.png) debe ser una tautología, igual a 1, en otras palabras. ¿Lo es?
debe ser una tautología, igual a 1, en otras palabras. ¿Lo es?
La fórmula equivalente a comprobar, eliminando sucesivamente las implicaciones y reduciendo, es:
![[(A'+B)B'] \Longrightarrow A' =](https://eltamiz.com/elcedazo/wp-content/cache/tex_0bcb28fdb43015895be9caa179d38082.png)

![[ (A'B') ]'+A' =](https://eltamiz.com/elcedazo/wp-content/cache/tex_33a5c4aebf8aa6704fc21bb17fa800f8.png)

El resultado siempre es 1: Tautología al canto. Luego el modus tollens es un razonamiento correcto. Y lo mismo con el resto de modus. Conociendo bien el modus ponens, pues, y las reglas del Cálculo Proposicional, que en realidad son las del álgebra de Boole, los demás… salen solos.
.
Sigamos un poco más. Cuando tenemos una cadena de premisas con implicaciones encadenadas, se puede alcanzar la conclusión usando extensivamente el modus ponens, en una suerte de propiedad transitiva encadenada, usando la conclusión del modus ponens anterior como premisa del siguiente, y así. Por ejemplo:






Es fácil de ver: al ir aplicando modus ponens sucesivos, vemos que:









Imaginad que la cadena de frases de ahí arriba es del estilo: “Soy español”; “si soy español me gusta el fútbol”; “si me gusta el fútbol veo la tele”; “si veo la tele me voy tarde a la cama”, etc, etc. Es evidente que, si todas las frases son ciertas, y sólo en ese caso, si soy español entonces… me voy tarde a la cama. Cosa que suele ocurrir, por cierto.
.
Un último ejemplo por hoy: Un vecino mío es de costumbres fijas. Muy fijas:
Si toma café, no toma leche.
Toma galletas sólo si bebe leche.
No toma sopa a menos que haya tomado galletas.
Hoy al mediodía se tomó una taza de café.
La pregunta es: ¿Ha tomado hoy sopa?[17]
Designemos, en primer lugar, las proposiciones elementales:
c: Toma café.
l: Toma leche.
g: Toma galletas.
s: Toma sopa.
Bien. Ahora escribamos las diferentes implicaciones del enunciado, que son la base deductiva:




Creo que no habrá problema alguno en entenderlo. Ahora ordenamos y reducimos:







La conclusión, pues, es s‘. La negación de s. Luego no, no tomó sopa hoy. Quizás comió patatas…
.
Basta por hoy, deduzco que ya ha habido bastante deducciones por esta vez… El próximo día, más píldoras lógicas de la mano de Don José Cuena, hablándonos vía el Túnel del Tiempo desde mis apolillados apuntes del curso 1973-74.
Disfrutad de la vida, mientras podáis.
- Aunque ciertamente hay casos en que… ¡a saber si está lloviendo o no! [↩]
- Igual podíamos haber tenido una, dos… o cincuenta premisas: da lo mismo. [↩]
- Fórmula importantísima, en realidad, pues es la base de todo el asunto deductivo. [↩]
- Tres premisas en el ejemplo; en el caso general será el conjunto de todas las premisas, claro. [↩]
- Acabamos de definir tautología como una expresión que siempre es verdadera, sean cuales sean los valores de verdad de las proposiciones individuales que la componen. Lo vuelvo a poner aquí para que tengáis a mano el significado de la palabrita. [↩]
- Y, ojo, no vale con plantarle una “V” a la brava y yastá… [↩]
- ¿Habéis detectado la doble implicación? Je, je, la Lógica es como un bulldozer… [↩]
- Imaginaos que la rayita de debajo de la p fuera más larga… cosas del Latex, o, mejor, mías, que no sé cómo hacerla más larga. [↩]
- Vale: ya sé que en realidad es más fácil comprobar la tabla de verdad, pero el método algebraico también funciona. [↩]
- Si la luz pasa cerca de una masa, se curva; La luz pasa cerca de una masa; Conclusión: La luz se curva. [↩]
- Si voy al cine, como palomitas; Ayer fui al cine; Conclusión: Ayer comí palomitas. [↩]
- La luz pasa cerca de una masa, pero no se curva: La Ley de la Relatividad General es falsa. Ayer no comí palomitas, así que o no fui al cine, o no es cierto que “si voy al cine como palomitas”. [↩]
- Bueno, más o menos chiquitín. [↩]
- Perdonad que los ponga en una imagen, pero es que estoy a punto de darme por vencido en mi lucha a brazo partido con el dichoso Latex… [↩]
- O un agricultor, o un fresador, o un vendedor, o una ama de casa… recordemos que esto funciona no sólo con “Leyes Universales” y fórmulas matemáticas, sino con proposiciones normalitas de la vida corriente. [↩]
- Él no lo sabía, claro, pero estaba “modusponensizando” de lo lindo. [↩]
- Y no, no le amenazaremos con ningún Hombre de la Bolsa si no se la toma. [↩]

The Eso que llamamos Lógica (VII) El proceso de deducción lógica. by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.










{ 19 } Comentarios
“o sea, la implicación es cierta si el antecedente es falso o verdadero el consecuente (o ambas cosas, claro)”
La frase induce a error. Un condicional no es cierta en todos los casos en el que su consecuente sea verdadero. En otros párrafos lo explicas mejor, en éste no.
La fórmula es, evidentemente: ( (A \wedge B \wedge C) \Longrightarrow D ) = 1
Por otra parte dicen tus apuntes:
“necesitamos de una buena implicación [...]Fórmula que en español leeríamos, más o menos: “Si ocurren simultáneamente A, B y C, entonces ocurre D, y esto pasa siempre, siempre“.”
¿Ves? a esto me refería yo el otro día. Dices que lo llamas deducción, pero lo que has escrito en esta parte del capítulo no es ninguna deducción, es una ley lógica o teorema. La diferencia entre ambas se ve muy clara en el cálculo axiomático que está compuesto de reglas de trasformación, axiomas y teoremas. Los tres son cosas distintas, aunque parecidas. Aunque a nivel práctico son semejantes, a nivel teórico una deducción está compuesto por varios enunciados mientras que un teorema es un único enunciado compuesto.
En fin, no te olvides de explicar mejor lo de el consequiente verdadero. Puede inducir a error al que lo lee.
@Ammonio:
Gracias, nuevamente, por comentar. Por cierto, el Latex no funciona en comentarios, ya lo habrás visto… qué se le va a hacer.
Bien: Lo que yo llamo “implicación lógica”, que tú llamas implicación material, es cierta cuando el antecedente es falso o verdadero el consecuente, o ambas cosas.
Es decir, p==>q es igual a p’+q. Y (p’+q) es verdadera cuando p (el antecedente) es falso o bien cuando q (el consecuente) es verdadero. El único caso en que (p’+q) es falso es cuando el antecedente es verdadero Y el consecuente, falso; en otro caso, es verdadero. Está bien en el texto.
Recuerda lo de “Si estornudo, cierro los ojos”. Si el consecuente es verdadero (tengo los ojos cerrados), la implicación es cierta, sea como sea el antecedente. O mejor, recuerda el caso del hospital: “Si gano la elección, construiré un hospital”. Si el hospital se construye, la promesa es verdadera, aunque el político no salga elegido.
Sigo creyendo (igual que en el artículo anterior) que estamos ante un problema de terminología. Lo que yo llamo “implicación lógica” (y es que es así como la llamamos los informáticos, aunque esté mal llamada), tú lo llamas “implicación material”, mientras que lo que yo llamo “deducción”, tú lo llamas “implicación lógica”, me parece deducir.
Es que lo informáticos somos así de raros: lo éramos en 1974 y lo seguimos siendo…
En cualquier caso, aquí está la demostración del proceso de deducción, a base de modus ponens, que te prometí en el artículo anterior.
En efecto, ten en cuenta que la implicación (material, lógica o mediopensionista, je, je, es decir, p==>q) no deja de ser más que una de las dieciséis posibles formas que puede adoptar una relación entre dos proposiciones que adoptan dos valores cada una (p y q). Su combinación (su tbala de verdad) da cuatro posibles valores en la tabla de verdad (V-V, V-F, F-V y F-F), y, claro, permutaciones de dos valores tomados de cuatro en cuatro son 2^4 = 16. Por ejemplo, otras combinaciones posibles de esas 16 son la disyunción (p+q), la conjunción (p·q), la doble implicación (p<==>q), la tautología (1), la contradicción (0), etc, etc, y así hasta 16.
En fin, espero que esto aclare un poco el malentendido.
Saludos.
Mac
“la implicación es cierta si el antecedente es falso o verdadero el consecuente”
Ahora, tras tu explicación, veo que no se trata de ningún error. Tú has escrito un enunciado molecular, por eso no hay error.
Pero ten en cuenta que alguien puede leer dos enunciados atómicos independientes. En este caso el segundo enunciado induciría a pensar que una implicación (por seguir tu terminología) es cierta siempre que el consecuente sea verdadero.
Yo en tu lugar, o quitaría la expresión para no dar lugar a ambigüedades, o matizaría mejor lo que quieres decir.
Muchos informáticos decis que la mayoría de las coordinadas copulativas tienen que ser formalizadas como disyuntivas (lo que parece una multiplicación lógica en el lenguaje coloquial, es en realidad una suma lógica). Estamos ante el mismo caso, pero inverso porque lo que haces es traducir desde un lenguaje formal a otro no formalizado. Es paradójico, pero si dices “”la implicación es cierta si el antecedente es falso Y verdadero el consecuente” (aunque esté mal traducido) la gente que no sabe lógica te va a entender mejor.
Es tu artículo, lo puedes dejar como está, pero es muy probable que la gente no lo entienda. Repito mi consejo: Yo en tu lugar, o quitaría la expresión para no dar lugar a ambigüedades, o matizaría mejor lo que quieres decir.
Por el otro lado, cambiando de tema y simplificando: sí, es un problema terminológico (pero también tiene mucho de conceptual).
A modo de ejemplo ¿puede ser un razonamiento cierto o falso? Tú mismo dices que no, que es imposible. Que a lo sumo resulta correcto o incorrecto.
Lo que yo llamo implicación formal, no es una deducción. La implicación formal es un tipo especial de enunciado y como tal puede ser cierto o falso, cosa que no podemos decir de las deducciones. Por ello mismo tampoco podemos decir que una implicación formal es correcta o incorrecta (son enunciados. Ni son razonamientos ni deducciones). La distinción entre implicaciones materiales e implicaciones formales son útiles para la lógica modal (la verdad de las primeras es posible, mientras que las de la segunda es necesaria). Su valor es diferente y no podemos utilizar las mismas reglas de transformación con ellas. ¿Conoces la diferencia entre la eliminación e introducción del generalizador y la introducción y eliminación del particularizador? pues una cosa semejante pasa con las implicaciones formales y materiales de la lógica modal.
Una implicación (sea formal o informal) es una expresión lógica. Una deducción es una concatenación de expresiones lógicas. No son lo mismo.
En fin, que me enrrollo demasiado y esta es tu serie.
“Es paradójico, pero si dices ”la implicación es cierta si el antecedente es falso Y verdadero el consecuente” (aunque esté mal traducido) la gente que no sabe lógica te va a entender mejor.”
Mmmm. Lo siento, pero no estoy de acuerdo. Si digo tal cosa probablemente la gente corriente, incluso si no sabe nada de lógica, pensará que para que sea cierta la implicación tienen que darse las dos frases a la vez, que ambas sean ciertas simultáneamente.
Si yo digo “Ganas a la lotería si juegas Y sale tu número”, yo creo que nadie entendería que ganaría si sólo compra el número, o si sólo sale tu número pero no lo has comprado…
Pero, claro: De lógica modal no sé nada, así que te sigo muy difícilmente, Ammonio, aunque me encantan tus comentarios porque me enseñan que más allá de mis pobres conocimientos hay un mundo lógico inmenso…
Es por ello que, al principio del artículo he vuelto a intentar dejar lo más claro posible que la lógica que yo sé y que aquí cuento no sabe nada sobre si las proposiciones atómicas son verdaderas o falsas: lo único que sabe es que, dados una relación entre varias proposiciones elementales y ciertos valores de verdad, qué le pasa a la proposición resultante, si es verdadera o falsa. Por ello, cuando citas que “la verdad de las primeras es posible, mientras que las de la segunda es necesaria”… me pierdo. Completamente. No entiendo cómo puede ser una implicación “necesaria”. Vamos, no es que lo entienda, es que ignoro la lógica modal, y, claro, me pierdo…
En fin, es mi intelecto, que no da para más.
Pero, oye: este es un sitio fantástico para que personas como tú, con exhaustivos conocimientos sobre esta materia, nos desasnen a los demás… Te invito a escribir un artículo (o varios) para que los ciegos como yo veamos la luz… Cuenta con toda nuestra ayuda para ellos.
Saludos
Mac
Tienes razón, la gente va a pensar que han de darse las dos condicones a la vez. Pero no tengo todas conmigo de que vayan a entender la frase.
Con respecto al otro tema…
Lo que se pretende diferenciar con la lógica modal son distintos modos de relación:
“Una implicación material es verdadera si su antecedente es falso o si su consequente es verdadero”.
“Una implicación formal es verdadera si la verdad del consecuente se sigue formalmente de la verdad del antecedente”.
¿Son equivalentes ambas definiciones? No. La segunda supone la primera, pero no abarca todos los casos de ésta. La primera comprende muchos más casos que la segunda porque es menos restrictiva.
En el primer caso (la material), sin atender a la materia del enunciado, y contemplando su tabla de valores vemos que es posible que el antecedente sea verdadero y el consecuente falso.
En el segundo caso (la estricta), no vamos a encontrar en su tabla de valores ni un caso en el que tengamos el antecedente verdadero y el consequiente falso porque es imposible que eso ocurra en una implicación estricta. Es imposible que exista porque de la verdad del antecedente se sigue necesariamente la verdad del consecuente.
Toda ley lógica (que no deja de ser una implicación estricta) se puede expresar como una implicación material (se hace siempre cuando se trabaja con la lógica clásica), pero no toda implicación material puede escribirse como una ley lógica.
Ha habido algún tiquismiquis que han recomendado que ninguna ley lógica se escriba bajo la forma de implicación material para evitar confusiones (ni siquiera en lógica clásica. Utilizaba un ancla en lugar de la flecha del condicional material para los casos de la estricta). Evidentemente pocos han seguido la recomendación. Eso, en lógica modal es básico distinguirlos.
Interesante razonamiento. Felicito al creador del post y a los comentantes.
@Ammonio:
Gracias por la explicación, pero… nada, que no me aclaro. Sigo sin ver la diferencia. ¿Qué es “seguirse formalmente la una de la otra? No lo entiendo. ¡Qué torpe soy, por favor!!
Quizás si nos dijeras cuál es la tabla de verdad de la “Implicación Formal” lo entendería. Ya sabes, el tamiz (:D) de la tabla de verdad aclara todas las dudas…
Siendo las proposiciones elementales p y q, y siendo los casos posibles V-V; V-F; F-V y F-F, es claro que para la implicación material (lo que yo llamo “implicación” a secas, o sea, p==>q), el resultado es: V; F; V; V, o p’+q, tal como explicas en tu comentario. Entonces…
¿Cuál sería el resultado de la implicación formal (digamos p$=>q, por llamarla de alguna manera que se distinga de la otra)? Supongo que será distinto del de la implicación material, porque en otro caso sería lo mismo… En fin, que estoy hecho un lío.
Gracias por tus comentarios.
Saludos.
Mac
¿Y sugieres que escriba un artículo? ¡pero si no sé explicarme! ¿Cómo voy a hacer tal cosa?
Su tabla de verdad es como la de la implicación material, pero como he dicho es más restrictiva:
si p es verdadero y q es verdadero=1
si p es falso y q es verdadero=1
si p es falso y q es falso también=1
El caso de que p sea verdadero y q sea falso simplemente no ocurre nunca en toda la tabla de verdad. Esto es lo característico de una implicación estricta: Tal caso no existe, es imposible que de la verdad del antecedente se siga la falsedad del consecuente. Es decir, es necesario que de la verdad del antecedente se siga la verdad del consecuente. Tal posibilidad está vedada, no ocurre, no nos la encontramos en estos casos…
Efectivamente, en lógica clásica no hay distinción entre las dos implicaciones ¿qué más da que un caso ocurra y en el otro sea imposible que ocurra?, no pasa nada. La lógica clásica sólo atiende a la sintaxis (a la forma de relación).
Pero en lógica modal no ocurre lo mismo. Se atiende a la sintaxis y a la semática (a los valores de verdad obtenidos) y por eso se diferencia entre implicaciones materiales y estrictas.
Podemos tener implicaciones marcadas como materiales, estrictas o simplemente no marcadas como nada (= meros condicionales lógicos). Material y extricta son expresiones que hacen referencia a la semática, nos dicen si son posibles o necesarios.
Si yo me encuentro con la expresión (es un ejemplo) “es necesario que si p entonces q” sé que, por ser necesario, en cualquiera de sus casos no me puedo encontrar con que p sea verdadero y q falso. Por lo tanto puedo afirmar tranquilamente “si p entonces q” porque sé que es cierto al 100%
Si por el contrario me encuentro con la expresión “es posible que si p entonces q”, en principio no puedo quitar la marca de posibilidad porque sé que hay 1/4 de posibilidad de que sea falso y un 3/4 de que sea cierto. No sabemos si es cierto o no (nos hemos cargado el principio de tercero excluido y declaramos que ni ciertos ni falsos: son posibles)
(Podríamos complicarlo con los conceptos de no- necesario (no confundir con posible) e imposible (que son los enunciados contradictorios)).
Como ves, la lógica modal trabaja con las relaciones (sintaxis) pero también con la semática de los enunciados (si son necesariamente ciertos, si son posiblemente ciertos, si es imposible que sean ciertos, o si no son necesariamente ciertos).
@Ammonio: Bueno, creo que voy entendiendo. Entre tus comentarios y que he brujuleado por la Wikipedia y otros sitios, creo que ya voy comprendiendo un poquito sobre Lógica Modal.
Por ejemplo, en la Wikipedia dan un ejemplo para distinguir entre “mi” implicación (lo que llamáis “condicional”) y la “implicación”. Éste es el ejemplo:
Condicional: “Si hoy es Martes entonces mañana es Miércoles”.
Implicación: “Hoy es Martes”, por tanto “mañana es Miércoles”.
Parece que el primero es exactamente como yo lo he descrito, pues dice que ” ‘Si A entonces B’ es una y única proposición y como tal una única afirmación” (estoy completamente de acuerdo, y he dedicado miles de palabras a intentar explicarlo).
Sin embargo, en la implicación asegura que ” En “A implica B” hay dos proposiciones y, por tanto, dos afirmaciones. Pero el valor de cada una es diferente. De modo que afirmando “A” como sentencia verdadera en su contenido semántico, se exige la afirmación de “B” como sentencia verdadera en su contenido semántico. Dicho de otra manera, la afirmación de la segunda depende de la validez de la primera”.
Y creo que lo he entendido: La clave está en lo de DOS afirmaciones. ¿Dos afirmaciones? ¿Dos?
¡Un modus ponens!
Veamos: Para mí, decir: “Hoy es Martes, por tanto mañana es Miércoles”, es lo mismo que decir que:
1- “Si hoy es Martes entonces mañana es Miércoles”.
2- “Hoy es Martes”.
Conclusión: “Mañana es miércoles”.
Dos afirmaciones (dos premisas) que, de ser verdaderas ambas, obligan a la certeza de la conclusión. Si la primera premisa es cierta y si además hoy es martes, entonces el uso del modus ponens nos asegura que Mañana será miércoles.
A mí me parece evidente, pero asumo que no debe serlo tanto cuando hay una serie de corrientes filosóficas que discuten y discuten sobre esto…
Lo que pasa es que, como somos unos vagos, en el lenguaje corriente “asumimos como cierta” la segunda premisa. Cuando decimos que “Si hoy es martes mañana es miércoles” estamos de alguna manera dando por sentado que “Hoy es martes” para que tenga sentido la frase, dado que si hoy es sábado… la frase no da ninguna información… ¡aunque sea formalmente cierta!
Además, déjame que sea un poco perverso. Retorciendo un poco la frase del martes y del miércoles, podíamos decir una equivalente:
“Si hoy es 4 de octubre, mañana es 5 de octubre”. De la misma forma que con la anterior, todos asumimos que para que sea cierta la frase, “Hoy debe ser 4 de octubre” (porque si hoy es 7 de septiembre no hay nada que decir de mañana a partir de esa frase), y por consiguiente diremos alegremente que “Hoy es 4 de octubre, por tanto mañana es 5 de octubre”, frase que todo el mundo daría como cierta y que tú llamarías seguramente una “implicación” como una casa.
Y entonces digo yo… ¡Error!
No es una frase cierta, es falsa, dado que al 4 de octubre de 1582 le siguió el 15 de octubre de 1582. Es decir, hay un contraejemplo para la implicación (perdón, el condicional material): “Si hoy es 4 de octubre, mañana es 5 de octubre”, y por tanto nada podemos decir de la conclusión, de lo que será mañana, por mucho que hoy sea 4 de octubre…
Vale, he hecho trampas, pero si pensamos en la Gravitación Universal durante los siglos XVII, XVIII y XIX, hasta la llegada de la Relatividad General, pues es lo mismo.
.
Luego he dado un vistazo a lo que se denomina “Lógica Modal” (lo que dice la Wikipedia, no más) y parece que, para empezar, los autores/estudiosos de la disciplina ni siquiera se ponen de acuerdo en el conjunto de axiomas que le dan soporte. Y, querido Ammonio, eso a mí me parece extraño, por no decir sospechoso.
Los axiomas de la Lógica de Primer grado están perfectamente establecidos, así como los del álgebra, etc. Si no somos capaces de ponernos de acuerdo en la base axiomática de la disciplina, ¿cómo nos vamos a poner de acuerdo en sus hallazgos? Claro que, repito, yo de Lógica “Humana” entiendo bastante poco, así que igual puedo estar equivocado de medio medio…
¡Qué agradable e instructiva conversación…!
Saludos. Y perdón por el comentario kilométrico…
Mac
Comienzo por el final: Hay dos corrientes que se asemejan, pero no son completamente iguales. La una hunde sus raíces en Aristóteles (son los comienzos de la lógica modal en el siglo XX y ésta estaba en pañales. Ejemplo Lukasiewizc). La crítica que haces sobre “el 4 de octubre…” puede afectarla en algún sentido, pero nunca de lleno. No al menos en el sentido en el que entiendo yo la lógica (que en esto sí que no hay ningún consenso aún).
La lógica, para mí, no estudia los contenidos de los enunciados ( para eso están las ciencias naturales y sociales). Creo que la lógica sólo debe de atender exclusivamente a las relaciones sintácticas por lo general, y sintácticas y semánticas en el caso de que nos interese por alguna razón. ¿Tú alguna vez has visto “p y no p”? Yo en la vida lo he visto. Es más, nunca lo veré, sin embargo me interesa la relación de contradicción. (he dicho “p y no p”, no he dicho “no es cierto que p y no p”
Y aquí es donde nace la segunda corriente de lógica modal (Lewis). Lewis a diferencia de Aristóteles no habla de hechos posibles, necesarios, imposibles o no-necesarios. Lewis habla de enunciados cuya verdad es necesaria, o cuya verdad es posible, o cuya verdad etc.
Breve excursus al margen de la lógica modal pero que tiene relación con ella: Wittgenstein (inventor de las tablas de verdad) decía que todo enunciado sobre un hecho es posible y nada más que posible porque en el mundo nada es necesario (si Ammonio no hubiera nacido, todo sería exactamente igual). Pero las tautologías y las contradicciones lógicas, sin ser hechos en sí, constituyen los límites de los hechos que pueden acontecer y que no pueden acontecer en el mundo. Fin del excursus
Sigo. Lewis nunca diría que “si hoy es 4 de octubre…” sea una implicación estricta. El tiene en mente enunciados que transcriben deducciones. No son meras deducciones porque éstas son un conjunto de operaciones y transormaciones lógicas, mientras que los otros son meros enunciados que los expresan. Y aquí no hay contraejemplos empíricos que valgan (pues estos enunciados no hablan sobre el mundo, estos expresan loslímites del mundo).
Parto, que se hace muy largo.
Dices “ni siquiera se ponen de acuerdo en el conjunto de axiomas que le dan soporte”
Que no te haga sospechar. En lógica clásica los sistemas axiomáticos son múltiples. Tienes el de Frege, el de Whitehead… Lukasiewizc creó un sistema axiomático de un único axioma. Todos tienen sus limitaciones y podemos coger el que más nos interesa. Podemos excoger entre sistemas de lógica proposicional, los de la lógica de enunciados, lógica de primer grado, lógica de segundo grado…
La lógica modal es más restrictiva que la lógica clásica. No hay ningún teorema de la lógica modal que no se encuentre demostrado por la lógica clásica, pero algunos teoremas de la lógica clásica (por cierto, teoremas de los que siempre se sospechó que fueran verdaderos por el sentido común) han quedado recusados por la lógica modal.
Las lógicas no clásicas han resultado muy útiles para la lógica en general.
Vuelvo a cortar para poder seguir.
Y ahora unas aclaraciones:
A) “Sin embargo, en la implicación asegura que ” En “A implica B” hay dos proposiciones y, por tanto, dos afirmaciones”.
No sé si lo has entendido bien así que voy a aclararlo porque es cierto sólo en parte.
1) La implicación formal o estricta es un único enunciado.
2) Concretamente es un enunciado metalógico en el que se relaciona la verdad semántica de las dos proposiciones simples que lo forman en este caso.
3) Lo de las comillas del ejemplo sirve para remarcar de dónde tomar los valores de verdad que estamos relacionando. Nada más que para eso.
B) “Veamos: Para mí, decir: “Hoy es Martes, por tanto mañana es Miércoles”, es lo mismo que decir que:
1- “Si hoy es Martes entonces mañana es Miércoles”.
2- “Hoy es Martes”.
Conclusión: “Mañana es miércoles”.
No son lo mismo aunque no se puede negar el parecido ya que el concepto de implicación formal (en este caso entendida al modo Aristotélico, pero con el otro ocurre lo mismo) se apoya en el concepto de demostración. Pero hay una diferencia fundamental: Mientras que el uno es un conjunto de enunciados concatenados (muchas veces con operaciones lógicas y transformaciones intercaladas) el otro es un único enunciado que no demuestra nada, sino que muestra unas relaciones de necesidad que podemos demostrar o que hemos demostrado anteriormente.
Sí, ya veo por dónde van los tiros… Estamos hablando más de (lo que yo llamo) Filosofía que de Lógica en sí.
Aristóteles basaba su idea del mundo en ciertos principios sobre los que edificar su sistema lógico de explicación del mundo, luego los escolásticos se basaron en él para establecer su propios principios (la existencia de Dios, como hizo Tomás de Aquino demostrando la omnisciencia, la omnipotencia, etc en sus famosas cuatro vías), etc.
Luego Descartes edifica toda su Filosofía en la duda sistemática que le lleva a definir su piedra angular sobre la que basar todo su pensamiento (el famoso “dudo luego pienso; pienso luego existo”); y más adelante otros pensadores como Kant, Heggel, Heidegger, Marx, etc toman otros principios fundamentales para llegar a demostrar y razonar su pensamiento (o para llevar el agua a su molino, según se vea).
Yo de esto sé muy poco, sinceramente. Lo estudié en Quinto de Bachiller hace cuarenta y pico años (bueno, siendo finales de los sesenta, a Marx no le estudié, claro, salvo para aprender que era como un demonio con cuernos y tridente), y lo tengo olvidado. Aunque debo reconocer que tampoco me interesaba mucho en aquella época.
Yo me quedo con la Lógica “matemática”, y dejo a filósofos, lingüistas, éticos y demás laya definir lo que es verdad y lo que no lo es… ¿Qué sé yo, pobre informático del tiempo del cuplé, de la verdad de las cosas…?
En fin, instructivísimo, como siempre.
Saludos
Ah, por cierto, lo de “p y no p” que comentabas, puesto así de claro yo tampoco lo he visto nunca, pero enredado en una discusión o argumentación, entonces sí lo he visto. Muchas veces.
Cuando tu jefe te dice que tienes la culpa pero no tienes la culpa de algo, o cuando un político dice que hará algo pero no lo hará o que es buena una cosa y su contraria, o que aquel tipo es un delincuente pero no es un delincuente, etc, etc. De paráfrasis de este estilo están llenos los periódicos todos los días. Sobre todo cuando se intenta negar a las hemerotecas.
Ejemplo de ahora mismo: “Sí, yo dije que el Matas ése era un ejemplo, pero no es un ejemplo, porque no es un buen tipo, a pesar de que es un buen tipo…”, y así, cienes y cienes.
No te sigo.
De ninguna manera estoy hablando de Filosofía ni de cuestiones filosóficas. Además, desde 140 años para acá cualquier rama de la lógica es lógica matemática.
Los sistemas axiomáticos lógicos son como los sistemas axiomáticos geométricos: Todos igualmente válidos mientras no sirvan para demostrar dos enunciados contradictorios.
O ¿Me vas a decir que el bueno es el de Euclides al igual que quiero entenderte que el bueno son los Pricipia Mathematica de Whitehead?
“Ejemplo de ahora mismo: “Sí, yo dije que el Matas ése era un ejemplo, pero no es un ejemplo, porque no es un buen tipo, a pesar de que es un buen tipo…”, y así, cienes y cienes”.
A esto es a lo que yo iba, a la lógica le interesa esa relación, no si en el mudo podemos hayar un ejemplo o un contraejemplo de tal afirmación.
Bueno, no, je, je. Me temo que el perdido soy yo…
Bueno, en el próximo artículo le toca al cálculo de predicados, que yo creo que será una piedrecita más en el camino, e igual facilita las cosas.
Este tipo de exposición bottom-up es lo que tiene, que muchas cosas que se echan de menos es porque aún no les ha tocado su turno…
Saludos
Mac
¡Por los dioses del olimpio! hallar, es hallar.
Bueno, bueno… quería esperar a terminar la serie para escribir un comentario felicitandote por la serie y demostrarte mi admiración, desde hoy tienes un fan más (bueno no, mentida, desde el primer día que leí ese maravilloso artículo sobre la 9a sinfonía de Beethoven). Encuentro absolutamente increíble la demostración del español con bigote al que le gustan los toros y el fútbol… he intentado hacerla yo mismo (antes de leer tu demostración, por supuesto, sino que gracia tiene…) y solo he sido capaz de llegar hasta la conclusión de que [ab(cd)'+bd+(ab)'], y a partir de aquí no tenía ni idea de cómo continuar… [Bueno, de hecho, había llegado a una ecuación ligeramente diferente al aplicar el Teorema de De Roger, que dice que (xy)'=(x'y') y que, sorprendentemente, resulta que es falso... ]
Y de hecho, menos mal que ya habías puesto este ejemplo antes de dejarnos esos razonamientos para practicar, porque si no no se me habría ocurrido sacar sumando común en el primero.
]
Y de hecho, menos mal que ya habías puesto este ejemplo antes de dejarnos esos razonamientos para practicar, porque si no no se me habría ocurrido sacar sumando común en el primero.
Por cierto, no te has confundido nunca y has sacado sumando común cuando no debías (osea, mientras manipulabas ecuaciones no boleanas)?
Bueno, que me voy por las ramas, excelente serie, de las mejorcitas que he leído (que he leído pocas… pero entre tu, Gustavo y J dejáis el listón muy pero que muy alto). Y por cierto, da la casualidad que justo dos días después de empezar la serie en clase de Tecnología empezamos el tema de neumática que, adivina… Se rige por álgebra de Boole
Bueno, ahora sí que me callo. En resumen, me está encantando la serie (me faltan dos artículos y casi me da pena terminar). Roger
¿Teorema de Roger? … mmmm …. no sé, no me suena…
¿(xy)’=(x’y')? No sé qué opinará Morgan de esto, je, je, pero creo que en el primer artículo de la serie ya se vio que (xy)’=x’+y’, así como que (x+y)’=x’y’. Cosas del Álgebra de Boole que siempre llaman la atención.
Y, por cierto, Roger, si has comprendido las bases del álgebra de Boole te aseguro que muchas, pero muchas de las asignaturas que vas a tener en el futuro te serán muuucho más sencilla. Es un auténtico bulldozer que derriba edificios lógicos incorrectos como el que lava. ¡Así de veces los he derribado yo!
Gracias por los elogios, le traspasaré su parte a Don José Cuena, esté donde esté…
Escribe un comentario