En el espeso y llenito-llenito de fórmulas, aunque tremendamente didáctico (espero), artículo anterior de esta serie sobre algo parecido a la lógica, vimos cómo en dos patadas Don José Cuena se despachó toda la definición del Álgebra de Boole. Al día siguiente (en realidad a la semana siguiente, porque las clases eran semanales, de dos horas cada una), a mediados de octubre de 1973, nuestro profesor apareció nuevamente a la hora en punto para seguir iluminándonos.
Sigamos con él, pues.
Bien, lo que Don José nos contó ese día fue cómo se definía una determinada relación en el álgebra de Boole, introduciendo para ello el signo  , que relaciona dos elementos del conjunto S. Evidentemente, la relación se llama “Menor o igual que”, hasta ahí podíamos llegar… En un álgebra de Boole se puede definir esta relación mediante la siguiente ecuación:
, que relaciona dos elementos del conjunto S. Evidentemente, la relación se llama “Menor o igual que”, hasta ahí podíamos llegar… En un álgebra de Boole se puede definir esta relación mediante la siguiente ecuación:
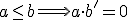
Como ya nos habíamos dado cuenta los de clase, o al menos la mayoría, que para algo el descubrimiento de la semana pasada había corrido como la pólvora, de que el álgebra de Boole era la que regulaba la Teoría de Conjuntos, rápidamente nos dimos cuenta de que la relación  en conjuntos era exactamente la relación “Contiene” que estudiamos años atrás en dicha teoría; mejor dicho, puesto que es “menor o igual que” y no “mayor o igual que”, en realidad se trata de la relación “Es Contenido por”.
en conjuntos era exactamente la relación “Contiene” que estudiamos años atrás en dicha teoría; mejor dicho, puesto que es “menor o igual que” y no “mayor o igual que”, en realidad se trata de la relación “Es Contenido por”.
Y claro, a partir de aquí todo fue coser y cantar. Si el conjunto A es contenido por el conjunto B, esto implica que la intersección de A y el complementario de B es el conjunto vacío… ergo  implica que
implica que  .
.
Naturalmente. Evidentemente. ¡Qué tontería!
En la figura anterior queda claro. B contiene a A, así que A es menor o igual que B, es decir,  . Por tanto, la intersección de A (el conjunto azul) con B’ (la zona gris clarita), que es el complementario de B (la parte amarilla), es el conjunto vacío, pues no tienen ningún elemento en común, luego es evidente que
. Por tanto, la intersección de A (el conjunto azul) con B’ (la zona gris clarita), que es el complementario de B (la parte amarilla), es el conjunto vacío, pues no tienen ningún elemento en común, luego es evidente que 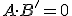 .
.
Toda la clase estuvo dedicada a demostrar las diferentes propiedades de tal relación, en demostrar que es una relación de orden, y, dentro de las de orden, de “orden parcial”, puesto que la relación no abarca a todos los elementos de S.
Por muy intimidante que parezca el párrafo anterior, en realidad es una tontería, es muy sencillo de entender: La relación  en los números naturales o en los reales, por ejemplo, es de orden total: cada uno de todos los números es o menor o mayor que todos los demás, pero tratando con conjuntos no tiene por qué ser así: pueden existir conjuntos que ni contienen ni son contenidos por otros conjuntos. El ejemplo más claro es lo que ocurre entre un conjunto y su complementario, por ejemplo, “los españoles” con “los extranjeros (los no españoles, vaya)”: ninguno de los dos conjuntos contiene al otro.[1]
en los números naturales o en los reales, por ejemplo, es de orden total: cada uno de todos los números es o menor o mayor que todos los demás, pero tratando con conjuntos no tiene por qué ser así: pueden existir conjuntos que ni contienen ni son contenidos por otros conjuntos. El ejemplo más claro es lo que ocurre entre un conjunto y su complementario, por ejemplo, “los españoles” con “los extranjeros (los no españoles, vaya)”: ninguno de los dos conjuntos contiene al otro.[1]
Y como toda buena relación de orden, cumple con las tres conocidas propiedades: es Reflexiva (es decir,  , pues todo elemento es menor o igual que sí mismo, en este caso estrictamente igual) es Transitiva (o sea, si
, pues todo elemento es menor o igual que sí mismo, en este caso estrictamente igual) es Transitiva (o sea, si  y
y  , entonces
, entonces  , lo que es bastante evidente), y es Antisimétrica (es decir, que si
, lo que es bastante evidente), y es Antisimétrica (es decir, que si  y simultáneamente
y simultáneamente  , entonces necesariamente
, entonces necesariamente  , lo que es también sencillo de entender).
, lo que es también sencillo de entender).
Antes de que digáis nada, en realidad la cosa es al revés: como en esta relación “ ” se cumplen las tres propiedades, entonces la relación “
” se cumplen las tres propiedades, entonces la relación “ ” es de orden. Ahora sí.
” es de orden. Ahora sí.
Como consecuencia de ser una relación de orden, se cumplen un par de propiedades adicionales:
Por un lado, si  entonces
entonces  .
.
Y por el otro, si  entonces
entonces 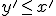 .
.
No voy a demostrar estas fórmulas: no son muy complicadas, por no decir que son intuitivas.[2] Quedémonos simplemente con esto: la relación “ ” en un álgebra de Boole es de orden parcial, y con eso nos sirve.
” en un álgebra de Boole es de orden parcial, y con eso nos sirve.
Le íbamos cogiendo el tranquillo a esto de la Lógica…
.
Siguiente día, siguiente semana. Hora en punto. Esto ya se está convirtiendo en todo un síntoma…
Hoy D. José nos hablará de La Forma Normal Disyuntiva de las expresiones (funciones) en un álgebra de Boole.
Mmmm. La… ¿qué? Sí, la Forma Normal Disyuntiva, ¿qué pasa? Será algo importantísimo para lo que sigue más adelante, así que hagamos menos chiribitas con los ojos, y vayamos al grano.
Primero habrá que definir qué es una función boleana. Toda aplicación de  que venga dada por una expresión en álgebra de Boole es una función booleana. Fácil, ¿no? … Venga, que es sencillo: dado que las dos operaciones definidas para el álgebra (+,·) son cerradas, es decir, que aplicadas a dos elementos de S dan como resultado otro elemento de S, el resultado de toda función f(x,y,z,…) expresada en álgebra booleana también pertenece a S.
que venga dada por una expresión en álgebra de Boole es una función booleana. Fácil, ¿no? … Venga, que es sencillo: dado que las dos operaciones definidas para el álgebra (+,·) son cerradas, es decir, que aplicadas a dos elementos de S dan como resultado otro elemento de S, el resultado de toda función f(x,y,z,…) expresada en álgebra booleana también pertenece a S.
…
Bueno, vale, ya voy.
Sea, por ejemplo, la función  definida en un sistema que obedece al álgebra de Boole.
definida en un sistema que obedece al álgebra de Boole.
Como tanto x como y como z son elementos de S, sea S lo que sea (y, por tanto, sus complementarios también lo son), cualquier operación (+,·) realizada sobre ellos (y entre ellos) y sus complementarios dará obligatoriamente un resultado que será también un elemento de S.
Truco: Pensad en conjuntos y lo veréis claro. Dados varios conjuntos cualesquiera y unidos e intersecados entre sí y sus complementarios como nos venga en gana, el resultado será siempre otro conjunto. Eso es una aplicación de  .
.
Teóricamente, las expresiones del álgebra de Boole podrían llevar constantes; de hecho hay dos constantes “de oficio”: los dos elementos neutros, 0 y 1. Pero las constantes en el sentido algebraico habitual no tienen mucho sentido:
¿Qué sería 6a, por ejemplo? Pues a, claro, dado que  . Como sabemos que
. Como sabemos que  [3] entonces
[3] entonces  , obviamente.
, obviamente.
¿Y qué sería 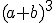 , entonces? Pues
, entonces? Pues 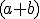 , natural, dado que
, natural, dado que  .
.
En definitiva, nunca aparecerán constantes en las expresiones que usaremos aquí (ni en las que usaremos normalmente en nuestra vida cotidiana de relación con el álgebra de Boole).
Pues bien, si tenemos una función booleana cualquiera en la que no aparecen constantes (por ejemplo,  , sin ir más lejos), entonces dicha función se puede representar como una suma de productos
, sin ir más lejos), entonces dicha función se puede representar como una suma de productos  , tales que:
, tales que:
1) En todo término  aparecen reflejadas todas las variables que aparecen en la fórmula original (bien complementadas, bien sin complementar). Todas ellas, sin faltar ni una.
aparecen reflejadas todas las variables que aparecen en la fórmula original (bien complementadas, bien sin complementar). Todas ellas, sin faltar ni una.
2) Todos los productos  son distintos entre sí.
son distintos entre sí.
.
Cabe decir aquí que a partir de ahora haré lo mismo que Don José hizo hace casi cuarenta años, simplificando la notación de las fórmulas de la misma manera que lo hacemos en el “álgebra normal”, la numérica: no escribiendo el signo “·”, salvo en los casos donde su uso sea preciso para hacer más descriptiva la fórmula. Es decir, la fórmula del ejemplo de arriba (y todas las demás) la escribiré preferentemente a partir de ahora de la siguiente manera:

Se entiende, ¿no? Pero recordad que “+” no es “suma” ni “·” es “multiplicación” en el sentido numérico habitual, sino que son “sumas booleanas” o “productos booleanos”, que ya veremos cómo se definen en según que sistemas… En conjuntos, por ejemplo, “+” es “Unión y “·” es “Intersección”, como ya sabéis. En otros sistemas, serán… otras cosas…
Paciencia.
.
Volviendo a la afirmación de hace un ratito (eso de que toda función se puede descomponer en sumas de productos), que seguro que os ha dejado con cara de haba, veremos cómo se llega con sencillez a esto, procediendo a la reducción sistemática de las expresiones en tres pasos:
Paso 1: Quitar sistemáticamente toda complementación a fórmulas entre paréntesis. Para ello usaremos extensivamente las Leyes de De Morgan.[4] Eran el Teorema 8 que vimos en el artículo anterior.
Por ejemplo, si tenemos  , quedaría, aplicando De Morgan,
, quedaría, aplicando De Morgan,  .
.
Al final de este paso sólo sólo habrá complementaciones de las variables individuales, pero no de operaciones con ellas (que no habrá complementaciones a paréntesis, vaya).
Paso 2: Quitar sistemáticamente el signo “·” entre paréntesis, aplicando la propiedad distributiva. Así,  quedaría
quedaría  .
.
Por ejemplo,  quedaría
quedaría  .
.
En realidad, ése es el resultado final, tras dos pasos. El primero dejaría  , y en un segundo paso quedaría
, y en un segundo paso quedaría  ; reordenando,[5] queda la fórmula del texto.
; reordenando,[5] queda la fórmula del texto.
Por supuesto, si algún término resulta que tiene simultáneamente una variable x y su complementaria, x’, al estar ambas multiplicándose entre sí, el resultado de esta multiplicación  es cero,[6] por lo que podemos eliminar sin pudor alguno el término completo. Así, si, por ejemplo, resultara un término
es cero,[6] por lo que podemos eliminar sin pudor alguno el término completo. Así, si, por ejemplo, resultara un término  , al ser
, al ser 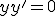 , queda
, queda  , y podemos eliminar el término completo, pues sabemos que
, y podemos eliminar el término completo, pues sabemos que  . Además, si quedan dos o más términos exactamente iguales, se pueden eliminar todos menos uno, puesto que sabemos también (mejor, seguimos sabiendo) que
. Además, si quedan dos o más términos exactamente iguales, se pueden eliminar todos menos uno, puesto que sabemos también (mejor, seguimos sabiendo) que  .
.
Bien, ahora tenemos ya la expresión reducida a una suma de productos distintos… pero no es suficiente, porque es posible que no en todos los productos estén representadas todas las variables, lo que era uno de los requisitos iniciales. De hecho, en el ejemplo anterior son 4 las variables (x,y,z,w) y ningún término tiene más que dos… Hay que hacer algo para que todos los términos tengan todas las variables, bien complementadas, bien sin complementar, que era el requisito previo, si os acordáis. Para solucionarlo:
Paso 3: Multiplicar los términos a los que les falte alguna variable x por  , que, como es igual a 1, no cambia el resultado.
, que, como es igual a 1, no cambia el resultado.
Por ejemplo, si son tres las variables de una cierta función f(x,y,z), y tenemos un término  (sin z), entonces éste se multiplica por
(sin z), entonces éste se multiplica por 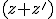 ,[7] quedando
,[7] quedando  .
.
Nuevamente, si como consecuencia de todas estas operaciones resultan dos o más términos iguales, se eliminan todos ellos menos uno, debido a la consabida idempotencia: 
En fin, tras la aplicación secuencial de estos tres pasos tenemos la misma fórmula original, bien masajeada, vale, pero la misma original, expresada de la forma pedida.
.
A esta forma de organizar las fórmulas booleanas se le llama Forma Normal Disyuntiva (FND), y veremos que es de gran utilidad más adelante… y hasta aquí puedo contar. Paciencia.
.
Veamos un ejemplo: Sea  . Con tres variables, como podemos ver: x,y,z. ¿Cuál es su Forma Normal Disyuntiva?
. Con tres variables, como podemos ver: x,y,z. ¿Cuál es su Forma Normal Disyuntiva?
Aconsejo a los que os interese todo esto que intentéis realizar el proceso vosotros solos, tenéis conocimientos y argumentos más que suficientes para hacerlo… y es fácil.
.
Según el paso 1, se eliminan los complementos en paréntesis (Ley de De Morgan).
 queda, en primer lugar,
queda, en primer lugar,
![(x+y+z)[(xy)'(x'z)']](https://eltamiz.com/elcedazo/wp-content/cache/tex_2356dd3a486cc0d4d71d2e1d0d0325d1.png) , que a su vez queda
, que a su vez queda
![(x+y+z)[(x'+y')(x+z')]](https://eltamiz.com/elcedazo/wp-content/cache/tex_31d8742976abeabed076da85d6474898.png) . Reordenando los productos (gracias a la propiedad
conmutativa) queda, por fin:
. Reordenando los productos (gracias a la propiedad
conmutativa) queda, por fin:
 .
.
Ahora aplicamos la distributiva (paso 2). Primero, sacamos en los dos primeros términos sumando común a x,[8] y entonces queda:
![[x+(y+z)z'] \cdot (x'+y')](https://eltamiz.com/elcedazo/wp-content/cache/tex_7172877b95d4fcc538fa37072f50135c.png) . Ahora aplicamos de nuevo la distributiva en el primer paréntesis, y queda:
. Ahora aplicamos de nuevo la distributiva en el primer paréntesis, y queda:
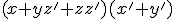 ; zz’ es cero, así que lo eliminamos, y queda:
; zz’ es cero, así que lo eliminamos, y queda:
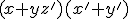 . Otra vez la distributiva y queda:
. Otra vez la distributiva y queda:
 , y otra vez más y queda, finalmente:
, y otra vez más y queda, finalmente:
 .
.
Como xx’ es cero, lo mismo que yy’, queda finalmente:  .
.
¿Ya está? Pues no, aún queda un poco.
Uno de los dos términos  no tiene la variable z, así que le multiplicamos por
no tiene la variable z, así que le multiplicamos por 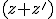 , que es, obviamente, 1 (paso 3), y tenemos que la fórmula original, ésa tan fea de ahí arriba, es equivalente a
, que es, obviamente, 1 (paso 3), y tenemos que la fórmula original, ésa tan fea de ahí arriba, es equivalente a  , mucho más bonita, dónde va a parar, que ya está en Forma Normal Disyuntiva.[9]
, mucho más bonita, dónde va a parar, que ya está en Forma Normal Disyuntiva.[9]
.
Prosiguió su exposición Don José contándonos que se podría definir una Forma Normal Disyuntiva Completa, que es, para n variables, la suma de todos los productos posibles de las n variables complementadas y sin complementar, que, como es fácil comprobar, son en total  .[10]
.[10]
Se demuestra fácilmente que una función cuya Forma Normal Disyuntiva sea Completa, es decir, que no le falta ni uno solo de los posibles términos que se pueden definir con las variables que la forman, es igual a la unidad (yo no voy a hacerlo aquí).
Por otra parte, se demuestra también fácilmente que, suponiendo como conjunto de valores posibles sólo 0 y 1, y dando a las variables valores arbitrarios entre estos, 0 ó 1, en la Forma Normal Disyuntiva Completa sólo habrá un único término que valdrá 1 y todos los demás, 0 (y su suma, 1, claro, al sumar muchos ceros y un único 1).
Esto es así porque para que un término (producto) cualquiera valga 1 en estas condiciones, todas las variables que lo componen tienen que valer 1, por lo que habrá sólo una combinación plausible: cualquier otra combinación de valores de las variables variará en al menos un valor de una variable, que será entonces 0 y anulará al término completo, al estar esa variable igual a cero multiplicando.[11]
…
No se me arremolinen… Un pequeño ejemplo servirá para entenderlo (recordad que los valores en este caso sólo pueden ser 0 y 1): Mirando la Forma Normal Disyuntiva Completa de un conjunto de tres variables, x,y,z, uno de los términos que la forman es, verbigracia,  . Este término sólo puede valer 1 para los valores siguientes de las variables: x=1; y=0; z=1. En estas condiciones, este término vale 1, ¿sí?
. Este término sólo puede valer 1 para los valores siguientes de las variables: x=1; y=0; z=1. En estas condiciones, este término vale 1, ¿sí?
Pero… ¿Qué les ocurrirá al resto de términos de la FNDC, por ejemplo el  ? Que variarán en al menos la complementación de una variable, en nuestro ejemplo en dos: x e y. Y al variar en alguna variable, quiere decir que alguno de los términos del producto ya no será 1, será 0, por lo que el producto completo será… cero. Efectivamente, para x=1; y=0; z=1, el producto
? Que variarán en al menos la complementación de una variable, en nuestro ejemplo en dos: x e y. Y al variar en alguna variable, quiere decir que alguno de los términos del producto ya no será 1, será 0, por lo que el producto completo será… cero. Efectivamente, para x=1; y=0; z=1, el producto  es cero. Y valen cero igualmente todos los demás términos, salvo el que cité al principio, el
es cero. Y valen cero igualmente todos los demás términos, salvo el que cité al principio, el  , que sí valdrá 1. Luego la FNDC se compone de la suma de un único término que vale 1 y siete que valen 0, por lo que la suma final es… 1. Siempre 1.
, que sí valdrá 1. Luego la FNDC se compone de la suma de un único término que vale 1 y siete que valen 0, por lo que la suma final es… 1. Siempre 1.
.
Vale, pero… ¿Para qué sirve esta dichosa Forma Normal Disyuntiva? Pues para saber si dos funciones son en realidad la misma, puesto que toda función que sea igual a otra tendrá su misma Forma Normal Disyuntiva.[12]
Esto nos será de gran utilidad más adelante, porque podemos representar la FND de cualquier función booleana en forma de tabla… veamos cómo quedaría la fórmula anterior, aquella  original, cuya Forma Normal Disyuntiva habíamos visto que era
original, cuya Forma Normal Disyuntiva habíamos visto que era  .
.
Representamos primero todos los valores posibles de la Forma Normal Disyuntiva Completa, todas las combinaciones posibles (en este caso serán  ), y entonces marcamos con 0 los términos que no están en su FND, y con 1 los que sí están…
), y entonces marcamos con 0 los términos que no están en su FND, y con 1 los que sí están…
Y el resultado es:
|
V: x |
V: y |
V: z |
|
|
x |
y |
z |
0 |
|
x |
y |
z’ |
0 |
|
x |
y’ |
z |
1 |
|
x |
y’ |
z’ |
1 |
|
x’ |
y |
z |
0 |
|
x’ |
y |
z’ |
1 |
|
x’ |
y’ |
z |
0 |
|
x’ |
y’ |
z’ |
0 |
Tachaaannn!!
Las cosas empiezan a tener sentido, ¿no? ![]()
Aquí se acabó la clase, aquel frío otoño de 1973. Y el artículo. Hasta otra…
Disfrutad de la vida, mientras podáis.
- En este caso, además, es que cada conjunto no contiene ni siquiera a uno solo de los integrantes del otro conjunto, no digamos a la totalidad… [↩]
- Pensad en conjuntos y veréis que efectivamente son evidentes. [↩]
- Teorema 1 del artículo sobre el álgebra de Boole, ¿recordáis? [↩]
- No son Leyes de Morgan, sino de De Morgan, pues son debidas al matemático indio-británico Augustus De Morgan. [↩]
- Aplicando la propiedad conmutativa. [↩]
- Por el Axioma 4 del álgebra de Boole, para los descreídos. [↩]
- Que es 1. [↩]
- Qué raro suena eso de “sacar sumando común”, ¿verdad? Pues más vale acostumbrarse… [↩]
- Sí, por si os lo estabais preguntando, también hay una Forma Normal Conjuntiva, que es parecida, pero sustituyendo los + por · y viceversa, así que lo que resulta es un producto de términos tal que cada uno de ellos es una suma que contiene todas las variables, complementadas o no, en vez de una suma de productos… La demostración es idéntica, en realidad, cambiando, en los pasos 2 y 3, el 1 por el 0 y el + por el ·, y viceversa. Todo en Álgebra de Boole es dual… [↩]
- Permutaciones de 2 elementos (complementado-sin complementar) tomados de n en n. [↩]
- Y lo mismo ocurre con la Forma Normal Conjuntiva, pero al revés: la Forma Normal Conjuntiva Completa será siempre cero. [↩]
- O Conjuntiva, cierto. Todo, absolutamente todo en álgebra de Boole es dual. [↩]

The Eso que llamamos Lógica (II) La Forma Normal Disyuntiva en el Álgebra de Boole by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.






{ 9 } Comentarios
¡Qué revelación esa última tabla! Gracias, Macluskey. Excelentísima serie.
Algo que se me acaba de ocurrir leyendo aquello de imaginar un conjunto S con solo el 0 y el 1: ¿No se podría demostrar esto usando la idempotencia y el hecho de que tengan que existir dos constantes? Si estoy en lo cierto(cosa que, con este cansancio que traigo, dudo severamente) seria algo tal que así:
Sabemos que tienen que existir al menos el 1 y el 0 gracias a los axiomas(y hemos decidido llamarlos 1 y 0, como diría un amigo for the lulz) la demostración de que solo pueden existir el 0 y el 1 sería tal que así:
Imaginemos podemos definir dos elementos cualesquiera de a y b distintos entre. Entonces podemos suponer que el “producto”(Por llamarlo de alguna forma) entre ellos será un número distinto e independiente del orden que se utilice, es decir:
a y b distintos entre. Entonces podemos suponer que el “producto”(Por llamarlo de alguna forma) entre ellos será un número distinto e independiente del orden que se utilice, es decir:
También sabemos que a·b es sumar a veces b y que b·a es sumar b veces a. Entonces, a través de la Idempotencia podemos decir que:
Es decir que a=b, llegando a una contradicción lógica. Es decir, no existen en el conjunto S dos elementos a y b distintos entre si. ¿Excepciones? El 1 y el 0 la explicación es la siguiente:
Si sustituimos a y b con los siguientes valores(y recordando que por la ley de conmutatividad da igual que número se elija para a y que número para b) a=0 y b=1 tenemos que:
Es decir que c=0 y, recordando que 0·a=0 la contradicción desaparece quedando pues que solo pueden existir en S dos elementos el 0 y el 1(u otros dos elementos con las mismas propiedades que les hemos dado al 0 y al 1)
En mi estado actual la demostración me parece coherente(pero como digo, estoy medio-dormido y no puedo asegurar que todo lo que diga en estos momentos sea real, díselo tu duendecillo pirómano). Que alguien le saque fallos será un autentico honor
Me acabo de fijar en un tamaño error en la última fórmula con LaTeX(he ahi la razon de porqué uno no puede dejar que un sonámbulo escriba ) debería de ser
) debería de ser 
Uhm… ¿esto lo sabemos? (En álgebra “normal” sí, pero en booleana… no lo hemos demostrado, ¿no?)
@Kratso: Como bien dice J,
“También sabemos que a·b es sumar a veces b y que b·a es sumar b veces a….” no lo hemos demostrado.
Es más, afirmo, no lo vamos a poder demostrar nunca. Porque en álgebra de Boole no es cierto. En el álgebra numérica normal, sí lo es, pero no en álgebra booleana.
Es fácil de ver: Piensa en nuestros amigos los conjuntos. Si tienes dos conjuntos A y B que, digamos, comparten algunos elementos, A·B son esos pocos elementos de la intersección entre ambos.
Ahora, si sumamos (unimos) “B” veces el conjunto “A” consigo mismo… conseguimos el mismo conjunto a, puesto que a+a=a.
O sea, A+A+…+A (B veces) es igual a “A”, no a “A·B”. Insisto, en álgebra booleana, que es de lo que trata el capítulo.
Además, querido Kratso… siguiendo con el ejemplo anterior… y siendo B como es un conjunto… ¿cómo podríamos sumar “B” veces algo?
De todos modos, como dicen los angloparlantes… “nice try!”
Gracias por comentar
Bueno, tampoco esperaba mucho, se me ocurrio escasos minutos antes de irme a dormir, jeje.
Pues yo siempre decía las leyes de Morgan
Gran artículo!
Saludos
@Juan Carlos: Nooo… si todos decimos las “Leyes de Morgan”, lo de “Leyes de De Morgan” es un “cultismo” a mitad de camino con “frikada”, que no dice nadie…
Pero… ¡Es que aquí somos todos muy cultos!!
Así que, pudiendo poner bien las cosas… ¿por qué ponerlas mal?
Saludos
Muy bueno el artículo @Macluskey, varias cosillas:
En el segundo ejemplo: en la parte en la que dices que no tiene sentido usar números distintos al 0 y 1, escribes la potencia 3 pero sólo escribes dos productos. (aunque, pues no importa mucho)
Cuál es la prueba de la Forma Normal Disyuntiva, es decir cómo se sabe que siempre se llega a ella.
Escribe un comentario