El Cedazo

Recreación artística de nuestra Vía Láctea en la cual se muestra nuestro Sol (punto rojo). NASA con la ayuda del CALTECH (2006)

En el anterior artículo de nuestra serie veíamos que, a pesar de encontrar una gran cantidad de problemas, los astrónomos fueron capaces de medir la distancia a las estrellas más cercanas. Tal empresa condujo también al descubrimiento de fenómenos maravillosos, como las estrellas binarias y la medición del brillo real de algunas estrellas.

La solución de estos problemas amplió el conocimiento de nuestro entorno, pero generaba aún más preguntas,  pues inevitablemente llegaban los problemas: ¿Dónde acaban las estrellas? y ¿A qué distancia se encuentra la más lejana? A fin de cuentas, la Tierra tiene un tamaño finito y lo mismo sucedía con el Sistema Solar. Pero al hablar del siguiente nivel, es decir, las estrellas, ¿estamos todavía en el dominio de lo finito o nos enfrentamos ya con lo infinito? El infinito, ese concepto que desde el principio preocupó a los hombres de ciencia. Hoy hablaremos del enfrentamiento del hombre con la vastedad del espacio. ¡Vamos pues!

A simple vista pueden contarse unas 6.000 estrellas, pero al enfocar telescopios cada vez más potentes sobre la superficie celeste se desvela la existencia de una cantidad cada vez mayor de ellas. Hacia 1800, las observaciones parecían llegar a un número casi infinito y, al parecer, a un universo carente de fronteras. Pero, una vez más, hablar de infinito es algo muy incómodo. Las primeras ideas que parecían atacar directamente este problema fueron expuestas por el astrónomo alemán Heinrich Wilhelm Matthäus Olbers (1758-1840). En 1826 sugirió la que más tarde se conoció como paradoja de Olbers: si suponemos que el universo tiene una extensión infinita y que las estrellas, las cuales se distribuyen de manera uniforme en todo el Universo y que tienen una luminosidad media equivalente en todo el espacio, son también infinitas, podemos llegar a conclusiones que ponen en aprietos la suposición misma de infinitud del Universo.

La paradoja de Olbers ha sido atacada desde una gran cantidad de puntos de vista y por muchos científicos. Actualmente cuenta con una solución aceptada, y si te gusta adelantarte doscientos años a la historia, seguro te interese el artículo publicado por Pedro que hace un gran tratamiento a la paradoja; con su amena escritura, seguro que aprenderás bastante. Volviendo a nuestra historia, miremos el argumento de Olbers:

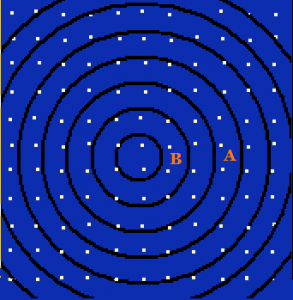
Cascarones de Olbers. Mientras las estrellas del cascarón A se ven mucho más tenues que las capas de la B, son mucho más numerosas. (Autor)

Supongamos al Sistema Solar situado en el centro del Universo infinito.^[1] Consideremos, para fines del razonamiento, tal universo dividido en capas concéntricas, como las de una cebolla.  El volumen de tales capas aumentaría con el cuadrado de la distancia.^[2]

Si la capa A se encuentra 3 veces más alejada que la capa B, aquella tendrá un volumen (3) ² o, lo que es igual, 9 veces mayor que el de la capa B. Por lo tanto, si las estrellas se distribuyen uniformemente, entonces la capa A tendrá nueve veces más estrellas que la B. Por otra parte, la luminosidad aparente de una estrella cualquiera disminuiría según el inverso del cuadrado de la distancia. Si la capa A es tres veces más distante que la B, suponiendo que la luminosidad media de las estrellas es aproximadamente constante en todo el espacio, las estrellas de la capa A tendrán un brillo aparente de solo (1/3) ² o 1/9 que una estrella cualquiera de la capa B. De esta forma, al sumar la cantidad de luz que llega de cada capa vemos que, a pesar de que la capa A tiene estrellas con un brillo de 1/9 que el de las de la capa B, en cambio hay 9 veces más estrellas, es decir, llega una luminosidad total de 9*1/9 de la capa B, es decir, la unidad. En pocas palabras, todas las capas en las que hemos dividido el universo, proporcionarían la misma cantidad de luz al Sistema Solar.

Al aplicar el mismo argumento sumando la luminosidad que proporcionan todas las capas, las cuales consideramos que son una cantidad infinita, tendríamos que sumar iteradamente y hasta el fin de los tiempos una cantidad igual (la contribución de cada capa). Al hacer esta suma infinita de términos iguales, por pequeños que estos sean, obtendríamos como resultado un valor infinito.

Suma de Olbers. A partir de las proposiciones, se obtiene un valor infinito de luminosidad. En este momento deberíamos estarnos asando por la luz de las estrellas. (Wikipedia)

Concluiríamos, por tanto, que nos debería llegar una cantidad infinita de luminosidad, lo cual, desde luego, no es lo que observamos.

Si el universo, a pesar de ser vastísimo, no es infinito, o si la luminosidad de las estrellas no es en promedio igual en todo el espacio, o si las estrellas no se distribuyen uniformemente en el Universo, tal suma podría no ser infinita, y no habría entonces paradoja. Por lo tanto, al menos una de las tres suposiciones que hemos tomado para iniciar el razonamiento debe ser incorrecta. ((Recordemos: Primero; el universo tiene una extensión infinita. Segundo: las estrellas se distribuyen de manera uniforme en todo el Universo y tienen una luminosidad media equivalente en todo el espacio, y tercero; las estrellas son infinitas.))

Lo que Olbers desconocía era que ya alguien estaba dando una posible respuesta al problema sin conocer siquiera los críticos efectos que implicaba la infinitud del espacio. Hablo de las cuidadosas observaciones realizadas por un viejo conocido para nosotros y que, como hemos visto, fue fundamental para el desarrollo de la astronomía: William Herschel (quien descubrió el planeta Urano y las estrellas binarias), cuyo retrato tenemos a continuación, ante quien no nos queda más que quitarnos el sombrero.

William Herschel, retrato de Lemuel Francis Abott (Wikipedia)

El nombre original de Herschel era Friedrich Wilhelm, descendiente de judíos como muchos hombres de la ciencia. Nacido en Hannover (actual Alemania), fue, al principio de su vida, por iniciativa de sus padres, un gran intérprete del oboe conformando, junto a su hermano, la banda de la guardia de Hannover. Como George II, el dirigente de Hanover era también rey de Inglaterra en esos tiempos, la guardia de Hannover se la pasaba viajando de Inglaterra a Alemania. En 1757, cuando estalló la guerra en los siete años entre Hannover y Francia, Fiedrich y su hermano fueron llamados a participar en la guerra. Sin embargo, Friedrich (con 19 años) presentó su dimisión y empezó una nueva vida en Inglaterra, adoptando su nuevo nombre: William.  En Inglaterra trabajaba como músico de iglesia y compuso alrededor de 24 sinfonías. Sin embargo, en 1773 conoció al astrónomo real Nevil Maskelyne y con él, William encontraría la pasión de su vida: la astronomía. El descubrimiento de Urano en 1781 le trajo gran fama y con ella la posibilidad de abandonar la música y dedicarse por completo a la astronomía. Fue nombrado astrónomo del rey y desde entonces, junto a su hermana Caroline, hicieron uno de los mayores aportes en la historia de la astronomía.

Déjenme abordar el trabajo de Herschel: Para todos los astrónomos, incluso en la antigüedad, era bien conocido que a lo largo de todo el cielo, atravesando las constelaciones de Orión, Perseo, Casiopea, Cisne, Águila, Sagitario, Centauro y Carena, se extiende una banda de débil luminosidad. En medio de las luces de la ciudad tal banda es invisible, pero en una noche sin luna y en el campo sin luces, tal banda constituye un espectáculo magnífico. Los griegos le dieron a esta banda, el nombre de galaxias kyklos (círculo lácteo) y los romanos de vía láctea, nombre con el que se le conoce actualmente. En 1610 Galileo observó la Vía Láctea a través de un telescopio y vio que no se trataba de una nube luminosa, sino de una colección enorme de estrellas muy tenues. Puede notarse también que las estrellas más brillantes son relativamente más abundantes en torno a tal banda, es decir, las constelaciones que son cruzadas por la banda son las de estrellas más brillantes. Esta disposición, que dista de la homogeneidad, contradice abiertamente la segunda proposición de Olbers: la de la distribución uniforme.

La Vía Láctea desde un observatorio en el hemisferio Sur (Observatorio de Arequipa)

En 1784 Herschel se interesó por una descripción cuantitativa de tal fenómeno. Para ello, tomó 683 regiones ubicadas arbitrariamente en toda la bóveda celeste y contó la cantidad de estrellas que podían observarse en cada una de ellas. Comprobó que el número de estrellas, en promedio, aumentaba en dirección a la Vía Láctea alcanzando un máximo en el plano de ésta. ¿Qué explicación admitía este resultado?

La existencia de una zona en el cielo en la cual se encuentra la mayoría de estrellas nos puede hacer pensar que en tal región éstas se apiñan de tal forma que la distancia entre vecinos se hace mucho más pequeña, mientras que, en los bordes, las estrellas se hacen mucho más distantes ocupando, de todas formas, todo el espacio, y tal apilamiento de estrellas es la razón por la que vemos mucho menos estrellas lejos de la franja.

Sin embargo, para Herschel era mucho más lógico suponer que la distancia media entre las estrellas era la misma, pero la distribución de estrellas no era uniforme, sino mucho mayor en el plano de la Vía Láctea, con lo cual el universo sería una especie de plato de estrellas de algunas decenas de años luz de grueso. En pocas palabras: las estrellas no es que existan en toda la bóveda celeste y se apiñen en la Vía Láctea, sino que simplemente se encuentran distribuidas uniformemente, pero en un arreglo en forma de disco con cierto grosor. Sería la perspectiva la que hace que veamos las estrellas más cercanas a nosotros como distribuidas uniformemente en el espacio, pero las más lejanas mucho más tenues y distribuidas en la franja que vemos como la Vía Láctea. Desde entonces, cuando se supo que vivimos en la franja de la Vía Láctea, los términos galaxia y Vía Láctea se utilizaron indistintamente para referirse al sistema de estrellas en general.

El disco galáctico según Herschel, en el cual se muestra el Sol en una posición cercana al centro (1785) (Dominio público)

Déjenme hacer una observación: notemos que la distribución de las estrellas en forma de plano no descarta que el numero de estrellas sea infinito, pues la cantidad de estrellas distribuidas en un plano crece de manera mucho más lenta a la forma en que decrece su luminosidad aparente^[3]. La suma de Olbers no sería ya en cascarones, sino en anillos, y sería de términos que, a pesar de ser infinitos, no son constantes sino cada vez más pequeños, y por tanto su suma puede converger a un cierto valor.

A Herschel le inquietó esta idea. Para él sonaba disparatado una extensión infinita del disco, así que, suponiendo una separación uniforme entre estrellas, trató de hacer una estimación burda del tamaño del disco galáctico. Observó que efectivamente la luminosidad observada no podía ser efecto de un plano infinito de estrellas. Conociendo la luminosidad de la franja y la densidad de estrellas, que él supuso igual a la de nuestro vecindario,^[4] la suma de Olbers debería corresponder a una suma finita y, conociendo el resultado (la luminosidad observada), pudo calcular la cantidad de estrellas necesarias: vio que el diámetro de la galaxia era, como máximo, de unas 800 veces la distancia media entre estrellas y como mínimo, unas 150 veces. El plano, pues, no sería infinito, y Herschel dio un argumento elegante.

A simple vista es posible notar que la Vía Láctea da la sensación de rodear el cielo por completo y su brillo ser uniforme en todo punto, así que a Herschel  le pareció lógico concluir que el Sol ocupa un lugar próximo al centro del disco. Observaciones posteriores realizadas a lo largo del siglo XIX no hacían sino refinar los detalles del sistema propuesto por Herschel. Con la invención de la fotografía y su aplicación a la astronomía, las observaciones mejoraron enormemente, y uno de los astrónomos que hizo uso de esta técnica fue el neerlandés Jacobus Cornelius Kapteyn (1851-1922), quien, al igual que Herschel, empezó el conteo de estrellas de cada magnitud en varias muestras de las superficie celeste. Sus resultados confirmaron la imagen de Herschel de una Galaxia “lenticular” con el Sol en el centro o cerca del centro. Sin embargo, las observaciones de Kapteyn arrojaban un diámetro, como máximo, de 2500 veces la distancia media entre estrellas y, como mínimo, 600 veces tal distancia, es decir, 23000 años-luz y 6000 años-luz, respectivamente. La mejora de instrumentos hizo posible que tales cifras aumentaran. La ultima medición del tamaño de la galaxia por el método de Herschel fue publicada en 1922 por el astronomo estadounidense Robert Tumpler (1886-1956), arrojando valores que situaban el tamaño de la galaxia a un mínimo de 11.000 y un máximo de 55.000 años-luz, dimensiones que mostraban una galaxia unas 475 veces más grande que la propuesta por Herschel.

Movimiento paralelo a la linea de observación. (Autor)

Como vemos, al parecer, Herschel había llegado mediante sus observaciones a algo que era aceptado desde mucho antes: la teoría heliocéntrica. Ya hemos visto que en tiempos de Copérnico se situaba al Sol en el centro del universo y a los  planetas y la bóveda celeste girando en torno a él. Sin embargo, el modelo objetivo con el cual se abordaba el estudio de los astros encontró que no había argumentos de peso que sustentaran la idea de que las estrellas giraran en torno al Sol. A pesar de que la homogeneidad de la Vía Láctea en el cielo, el descubrimiento de los movimientos propios de las estrellas parecía refutar tal idea, dado que las observaciones mostraban un movimiento aleatorio de éstas. El Sol estaría en el centro de la galaxia pero las estrellas no giraban en torno al Sol.

Era lógico ver que las estrellas no deberían girar en torno nuestro; los modelos gravitacionales propuestos por Sir Isaac Newton (de los cuales hablaré dentro de un par de artículos) predecían que, de hacerlo, las estrellas deberían girar en torno a un centro masivo, mucho, pero mucho, más masivo que el Sol. De ser así, el Sol también giraría en torno a ese centro; esto es: no estaría estático. A partir de tal razonamiento, en 1783, Herschel abordó la tarea de detectar un posible movimiento de nuestro sistema solar con respecto a las estrellas más cercanas. Veamos el método que utilizó.

Movimiento perpendicular a la dirección de observación. Los objetos más cercanos tienen movimiento propio mayor. (Autor)

Supongamos las estrellas fijas en el espacio y distribuidas uniformemente como los soldados formados en filas y columnas. A un grupo de estrellas alejadas de nosotros, las observaríamos muy cercanas entre sí mientras las más cercanas aparecerán relativamente más separadas. Este fenómeno, como dijimos antes, es la perspectiva. De esta forma, si nos acercamos a un conjunto de estrellas, éstas (como se observa en la animación de arriba a al derecha) aparentemente se separarían entre sí. Por otro lado, aquel grupo del cual nos alejamos parecería amontonarse gradualmente (estos efectos parecerían enmascarados, pues las estrellas no permanecen quietas, pero tal enmascaramiento no es total).

Por otro lado, aquellas estrellas situadas perpendicularmente a la dirección de movimiento (como se observa en la imagen a la izquierda) tendrán un movimiento propio mayor y opuesto al movimiento solar. Realizando este tipo de observaciones fácilmente podemos notar hacia dónde nos movemos en relación con las estrellas. Aunque eran pocos los movimientos propios conocidos en tiempos de Herschel, pudo basarse en estos y en el razonamiento anterior. Vio que el Sol, efectivamente, se mueve, y que lo hace en dirección a algún punto situado en la constelación de Hércules. Estimación nada mala, pues las mediciones actuales localizan tal punto o “ápice” en las afueras de la constelación de Lira, vecina a la de Hércules. El Sol se mueve hacia este punto a una velocidad (con respecto a las estrellas más cercanas) de unos 19 km/s.^[5]

Geniales los aportes de Herschel a nuestro conocimiento del cielo, ¿no es así? Tan avanzada era la mente de William Herschel para sus tiempos que el siguiente avance en nuestra concepción del universo sólo se daría casi 150 años después de los descubrimientos de este anglo-alemán, que fue especialmente admirado por Napoleón y (¿para qué ocultarlo?) por este servidor. ¿A qué me refiero con avance en nuestra concepción del universo? No hay más que acompañarnos en la siguiente entrada, en la cual, les adelanto, nos enteraremos de cómo nos dimos cuenta de que no nos encontramos en el centro de la galaxia, como pensaba Herschel, sino lejos del centro, como muestra la imagen con la que he empezado el artículo.

Hasta la próxima.

1. Obviamente hablar de “centro” de un Universo infinito es algo complicado de imaginar, pero en un infinito cualquier punto puede ser el centro. [↩]
2. Ojo, el volumen relativo de las capas (esto es, el volumen de una con respecto a otra) no aumenta con el cubo, como cabría pensar, sino con el cuadrado. Estamos hablando de capas del mismo grosor, no de esferas. [↩]
3. La cantidad de estrellas en un plano crece en proporción directa al radio, mientras que la luminosidad decrece en proporción al inverso del radio al cuadrado. [↩]
4. Unos mal contados diez años luz [↩]
5. Cientos de veces más rápido que el sonido en el aire [↩]

The Descubriendo nuestra galaxia. La paradoja de Olbers y la galaxia-disco. by César Augusto Nieto, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.