El Cedazo

Jenga. Fuente: Wikipedia.

Hola a todos! Tras llevar un tiempo siguiendo esta página web me he animado a colaborar escribiendo algunos artículos sobre el segundo principio de la termodinámica.

Para empezar, he de decir que este artículo está lleno de simplificaciones y que no soy para nada un experto en el tema, así que confío en que los tamiceros/cedaceros que sepan de esto me ayuden a corregir los errores que pueda haber en el artículo, así como ayudarme a resolver las dudas que surjan.

Una vez dicho esto, vamos a ello.

SEGUNDO PRINCIPIO DE LA TERMODINÁMICA Y ENTROPÍA

Podemos observar que en la naturaleza existen muchos procesos que ocurren con mucha facilidad en un sentido pero que es mucho más difícil que sucedan en el sentido contrario: es fácil tirar al suelo una botella de vídrio, haciendo que se se rompa en pequeños trozos de cristal pero, sin embargo, no es nada fácil reunir todos esos trozos y reconstruir la botella; por otro lado, los que hayáis jugado al jenga —juego en el que hay que quitar bloques de una torre y colocarlos en la parte superior sin que ésta se caiga— habréis comprobado que basta con quitar unas pocas piezas del nivel inferior para que la torre se caiga, pero cuesta mucho más trabajo reconstruir la torre; incluso en el instituto es muy fácil que los alumnos salgamos de  estampida cuando suena el timbre al final de la última clase, pero es más difícil hacernos entrar en clase cuando llega el profesor.

El segundo principio o segunda ley de la termodinámica explica a qué se debe que muchos sucesos “prefieran” suceder en un sentido que en el contrario. Éste, dice lo siguiente:

En un sistema aislado la entropía tiende a incrementarse con el paso del tiempo hasta que éste alcance un estado de equilibrio (estado en el que no se producen cambios de presión ni de temperatura).

Pero… ¿Y qué demonios es eso de la entropía?

La manera más fácil de definir la entropía es la siguiente: ¿qué tienen en común todos los procesos que hemos visto anteriormente? Comprobaréis fácilmente que en los procesos vistos anteriormente ha aumentado el desorden: los cristales estaban más ordenados cuando constituían la botella que tras esparcirse por el suelo de manera aleatoria; los bloques de la torre estaban más ordenados antes de que ésta se cayera, o, si me apuráis, en el ejemplo tonto del instituto los alumnos estábamos más ordenados en clase que al salir en desbandada al oír el timbre.

Por otro lado, hay que decir que se considera desorden como sinónimo de homogeneidad o “igualdad”. Esto es muy importante, ya que hay quien, usando su sentido común, podría considerar que un sistema cuyas moléculas están distribuidas homogéneamente (o uniformemente ) está ordenado. La entropía, por tanto, se puede definir así: 

La entropía es una magnitud que mide la cantidad de desorden u de homogeneidad que hay en un sistema: la entropía será mayor cuanto más desordenado esté el sistema.

Otro concepto que es importante conocer es el de sistema aislado: un sistema aislado es aquel que no comparte ni energía ni materia con su entorno. Obviamente, es imposible conseguir aislar completamente un sistema del resto del entorno, por lo que el único sistema aislado que conocemos no es otro que el universo entero, ya que no tiene nada en su entorno que pueda interaccionar con él. Sin embargo, a pesar de no existir ningún sistema aislado además del universo, existen muchos otros sistemas que pueden estudiarse como sistemas aislados, consiguiendo obtener aproximaciones casi perfectas.

Ludwig Boltzmann. Fuente: Wikipedia.

Según este principio, todo en la naturaleza tiende a alcanzar un estado de equilibro, algo evidente para cualquiera que mire a su alrededor. Sin embargo, cuando se formuló por primera vez, a mediados del siglo XIX, nadie era capaz de demostrar por qué. No fue hasta la década de 1870 cuando Ludwig Botzmann, uno de los creadores de la mecánica estadística, se basó en ésta para demostrar que la segunda ley de la termodinámica no era más que una ley probabilística.

Para ello, se apoyó en que de entre todos los microestados posibles de un sistema sólo unos pocos están ordenados. Por ejemplo, si tiramos 4 monedas al suelo podemos obtener los siguientes resultados: cara-cara-cara-cara, cara-cara-cara-cruz, cara-cara-cruz-cara, cara-cara-cruz-cruz, cara-cruz-cara-cara, cara-cruz-cara-cruz, cara-cruz-cruz-cara, cara-cruz-cruz-cruz, cruz-cara-cara-cara, cruz-cara-cara-cruz, cruz-cara-cruz-cara, cruz-cara-cruz-cruz, cruz-cruz-cara-cara, cruz-cruz-cara-cruz, cruz-cruz-cruz-cara, cruz-cruz-cruz-cruz.

Como podréis ver en este caso, de los 16 casos posibles sólo dos están completamente ordenados (coloreados de rojo), 6 de ellos están medio ordenados (pintados de verde) y 8 de ellos están completamente desordenados (coloreados de azul). Podemos ver entonces, que la tendencia de los sistemas a desordenarse (o lo que es lo mismo, de aumentar su entropía) es debido a las probabilidades, ya que los sistemas desordenados son mucho más probables que los ordenados.

En el ejemplo anterior vemos que hay un considerable número de posibilidades de que tras el experimento el sistema acabe ordenado pero, ¿qué pasaría si lanzáramos al suelo no 4, sino 2000 monedas? Aquí aparecería un teorema de probabilidades, la ley de los grandes números, que afirma que cuantas más veces se repita un suceso aleatorio, más tenderá el valor promedio a acercarse al valor teórico. En la imagen de debajo podéis ver una simulación aleatoria donde se comprueba que al aumentar el número de lanzamientos, el porcentaje de caras y de cruces tiende a acercarse al al valor teórico, es decir, al 50%.

Los sistemas con los que se trabaja habitualmente están formados por una cantidad inmensa de moléculas, por lo que, debido a este teorema, en un sistema aislado, a no ser que estemos trabajando en órdenes de magnitud o de tiempo realmente pequeños, la probabilidad de que la entropía disminuya es casi nula.

Boltzmann, también consiguió definir matemáticamente el concepto de entropía mediante la siguiente fórmula:

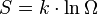
Donde S es la entropía, k es la constante de Boltzmann, ln es el símbolo del logaritmo neperiano y Ω el número de microestados posibles de un sistema (todas las maneras distintas en las que se pueden combinar las moléculas).

OTRAS DEFINICIONES DEL SEGUNDO PRINCIPIO DE LA TERMODINÁMICA

Como hemos visto antes, debido a las probabilidades los sistemas tienden a desordenarse u homogeneizarse. Con la energía ocurre exactamente lo mismo, por lo que otra manera de definir el segundo principio de la termodinámica es la siguiente:

En un sistema aislado, cuando una parte interacciona con otra parte, la energía tiende a repartirse por igual hasta que el sistema alcance un equilibrio térmico.

Por otro lado, la temperatura de un cuerpo mide el movimiento de las moléculas que lo componen, siendo tan sólo una forma de energía, por lo que el segundo principio de la termodinámica también se puede definir así:

Cuando tenemos en un sistema aislado dos cuerpos a distinta temperatura, con el paso del tiempo el cuerpo a mayor temperatura tenderá a ceder energía en forma de calor al cuerpo a menor temperatura.

Ahora, supongamos que tenemos un litro de agua a 80ºC. Esa energía se podría usar para calentar un litro de agua a 0 ºC hasta que ambos alcanzaran una temperatura de 40 ºC. Así, ahora tendríamos 2 litros de agua a 40 ºC que se podrían utilizar para calentar 2 litros de agua a 0 Cº y así obtener 4 litros de agua a 20 ºC. Estos a su vez… Vemos que siempre podemos usar agua más caliente para calentar agua más fría pero, ¿es posible conseguir que dos de esos litros de agua a 20 Cº transmitan parte de su energía a los otros 2 litros de agua que también se encuentran a 20 Cº para así obtener por un lado dos litros de agua a 0 ºC y por otro 2 litros de agua a 40 ºC  (sin añadir energía extra al sistema)?

¡NO! Este principio nos dice que eso es imposible. Se puede ver por tanto, que tras realizar sucesivas mezclas tendremos todo el agua a la misma temperatura y que la energía de una determinada cantidad de agua ya no se podrá usar para calentar otra cierta cantidad de agua, ya que ambas cantidades se encontrarán a la misma temperatura (se encontrarán en equilibrio térmico). Dicho de otro modo, conforme mezclamos cantidades de agua a temperaturas distintas aumentará la parte de la energía que no se puede usar para efectuar un determinado trabajo (en este caso el calentar más agua). Así, podemos ver que la entropía, además de definirse como la cantidad de desorden de un sistema, se puede definir de la siguiente manera:

La entropía es la parte de la energía que no se puede utilizar para realizar un determinado trabajo.

CONSECUENCIAS DE LA SEGUNDA LEY DE LA TERMODINÁMICA.

Esta ley implica que es imposible construir una máquina capaz de producir un trabajo todo el tiempo a base de intercambiar calor con una sola fuente térmica. Esto se debe a que como hemos visto antes, con el paso del tiempo aumentaría la entropía, o lo que es lo mismo, la parte de la energía que no puede producir un determinado trabajo.

Evolución del universo. Fuente: Wikipedia

Por otro lado, el segundo principio de la termodinámica tiene una consecuencia inevitable: el tiempo tiene un sentido determinado. Como hemos visto al principio, el universo es un sistema aislado donde la entropía tiende a aumentar con el tiempo, es decir, conforme el universo evoluciona, su entropía aumenta con él. Un viaje atrás en el tiempo implicaría una disminución de la entropía, lo que violaría la segunda ley de la termodinámica. Esto descarta la concepción cíclica del tiempo que estuvo tan presente en la antigüedad.

También se descarta la teoría del universo oscilante. Como todos sabréis, la teoría del Big Bang dice básicamente que hace unos 13.500 millones de años hubo una “explosión” que originó el Universo y éste todavía se está expandiendo como resultado de esta explosión. Según la teoría del universo oscilatorio la fuerza de atracción gravitatoria entre las galaxias provocará que la velocidad de expansión del Universo vaya disminuyendo, hasta que éste se comience de nuevo a contraer, llegando a “un sólo punto” (Big Crunch), donde se producirá de nuevo un Big Bang, luego otro Big Crunch y así infinitas veces. Según esta teoría, el universo en el que vivimos podría haberse formado y destruido numerosas veces. Sin embargo, según la segunda ley de la termodinámica, la entropía del universo tiende a aumentar con el tiempo, por lo que cada universo que se formara no sería exactamente igual al anterior. De hecho, al cabo de un determinado número de contracciones y expansiones, la energía se igualaría en todo el universo alcanzando el equilibrio térmico (muerte térmica del universo). Aparte de esto, las últimas mediciones indican que el universo se está expandiendo de manera acelerada, pero eso es otra historia.

Así, parece ser que el universo está destinado a alcanzar un estado de equilibrio en el que ya no será posible ningún proceso termodinámico. Afortunadamente, todavía falta mucho tiempo hasta que esto ocurra.

Bueno, y hasta aquí llega la entrada de hoy. En el próximo artículo hablaré sobre la posibilidad de violar el segundo principio de la termodinámica.

The Segundo principio de la termodinámica I by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.