Tras hablar de aplicaciones entre conjuntos vamos a hacer un pequeño inciso para curiosear un poco sobre el infinito (siguiendo la estela a esta entrada de Pedro).
Tras hablar un poco sobre lo que es un conjunto vamos a hablar de cosas que podemos hacer con ellos. Vamos a usar como ejemplo el de los malvados alienígenas babosos. Si recordais de la entrada de Pedro, estos alienígenes se había construido una nave que contenía infinitos soldados. Mucho ojo, un número infinito, pero que se puede contar. Esto es, usando los conocimientos de la última entrada, que existe una aplicación biyectiva entre el conjunto de soldados en la nave y los número naturales. Como existe una aplicación biyectiva, para nuestros intereses el conjunto de soldados y el de números naturales son indistinguible. Llamemos a este conjunto de soldados, para abreviar,  .
.
A este tipo de conjuntos se los llama conjuntos numerables.
En una primera instancia, el general envía 10 soldados más a la nave. Formalmente esto sería unir el conjunto de los 10 soldados (que denotaremos, por ejemplo, como  ) con nuestro conjunto de soldados
) con nuestro conjunto de soldados  . Esto formalmente se escribe así:
. Esto formalmente se escribe así:

Lo sorprendente es que al final resulta ¡que no tenemos más soldados que antes! De hecho, como vimos en el segundo ejemplo, si juntamos dos naves con infinitos soldados seguimos teniendo el mismo número de soldados. Esto es formalmente lo siguiente:
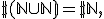
donde  antes de un conjunto significa “el número de elementos” que tiene ese conjunto. La demostración de esa afirmación esta en la entrada de Pedro y se llevará un gallifante el que escriba correctamente la aplicación biyectiva entre ambos conjuntos.
antes de un conjunto significa “el número de elementos” que tiene ese conjunto. La demostración de esa afirmación esta en la entrada de Pedro y se llevará un gallifante el que escriba correctamente la aplicación biyectiva entre ambos conjuntos.
Ahora bien, el tercer ejemplo de la entrada de Pedro es un conjunto es distinto. En ese ejemplo lo que tenemos es un metacarguero que tiene infinitos cargueros de  soldados. Es como si por cada soldado pusiéramos infinitos más. Si lo pensamos de forma “geométrica” es como si pusiéramos a todos los soldados de un carguero en fila india, y luego perpendicularmente, por cada soldado, hicieramos otra fila de infinitos soldados. Dibujo al canto.
soldados. Es como si por cada soldado pusiéramos infinitos más. Si lo pensamos de forma “geométrica” es como si pusiéramos a todos los soldados de un carguero en fila india, y luego perpendicularmente, por cada soldado, hicieramos otra fila de infinitos soldados. Dibujo al canto.
En el dibujo, habría un soldado por cada esquina de los cuadraditos que se forman. Formalmente a esto se le llama el producto de dos conjuntos y se denota:

Normalmente a un elemento de este conjunto se le denota como  . En nuestro ejemplo sería decir que
. En nuestro ejemplo sería decir que 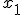 el número de soldado y
el número de soldado y  el número de carguero en el que está. Por ejemplo, si Xugthudz es el soldado número 1268 de la nave 57, Xugthudz es el elemento (1268,57).
el número de carguero en el que está. Por ejemplo, si Xugthudz es el soldado número 1268 de la nave 57, Xugthudz es el elemento (1268,57).
A primera vista parece que hay un montón de soldados, ¡¡pero resulta que al final seguimos teniendo el mismo número de soldados!! La forma de demostrarlo es distinta a la que propuso Pedro (ésa la usaremos en el plato fuerte de la noche) y es más visual. Una cosa muy importante, dar una aplicación biyectiva entre ese conjunto y los naturales es simplemente numerar cada soldado del dibujo. En el siguiente dibujo doy la idea de como se construye la aplicación.

Forma de poner en fila india a los soldados de la meta-nave.
Ahora bien, estos malvados bichos han decidido que lo del metacarguero es para nenas. De hecho, creen que un meta-metacargueros lo es (un gallifante para el que escriba formalmente el conjunto ![]() ). Es más, van tan sobrados que un meta-
). Es más, van tan sobrados que un meta- -meta carguero es también para nenas.
-meta carguero es también para nenas.
Mucho ojo con esta notación: generalmente, cuando se escriben puntos suspensivos y se quiere dejar explícito cuantas repeticiones se realizan se suele poner el número precedido por un paréntesis. Así, por ejemplo,  es el equivalente a
es el equivalente a  . Otra forma de denotar lo mismo es con unas llaves por arriba o por debajo de los puntos suspensivos y el número de repeticiones. Por razones técnicas no se usa esa notación aquí
. Otra forma de denotar lo mismo es con unas llaves por arriba o por debajo de los puntos suspensivos y el número de repeticiones. Por razones técnicas no se usa esa notación aquí ![]()
Aunque probablemente el uso más común que se le da a esta notación es la de  -ésima derivada de una función. Los que hayan estudiado matemáticas en segundo de bachiller habrán estudiado o bien la notación de Lagrange o bien la de Leibniz para la derivada de una función (hablaremos en su momento sobre qué es la derivada de una función pero eso será más adelante en la serie).
-ésima derivada de una función. Los que hayan estudiado matemáticas en segundo de bachiller habrán estudiado o bien la notación de Lagrange o bien la de Leibniz para la derivada de una función (hablaremos en su momento sobre qué es la derivada de una función pero eso será más adelante en la serie).
Los matemáticos generalmente usamos la notación de Lagrange (en algunas ramas es común también la de Newton, ver el artículo de la wikipedia), es decir, usamos  para la función, la primera, la segunda y la tercera derivada, respectivamente, pero
para la función, la primera, la segunda y la tercera derivada, respectivamente, pero 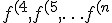 . Los físicos (y seguro que los ingenieros) estáis más acostumbrados a la notación Leibniz:
. Los físicos (y seguro que los ingenieros) estáis más acostumbrados a la notación Leibniz:  que representan una función, su derivada, su segunda derivada, etc. La primera es más compacta pero cuando la cosa se complica da muchos problemas notacionales que la notación de Leibniz resuelve. Por si te pierdes con este super-meta-carguero, la notación formal sería:
que representan una función, su derivada, su segunda derivada, etc. La primera es más compacta pero cuando la cosa se complica da muchos problemas notacionales que la notación de Leibniz resuelve. Por si te pierdes con este super-meta-carguero, la notación formal sería:

Geométricamente, sería un espacio  -dimensional. Si en el otro ejemplo pintamos a los soldados en un folio plano, ahora necesitaríamos ¡un folio de
-dimensional. Si en el otro ejemplo pintamos a los soldados en un folio plano, ahora necesitaríamos ¡un folio de  dimensiones! A los soldados de este meta-
dimensiones! A los soldados de este meta- -meta carguero los podíamos denotar como
-meta carguero los podíamos denotar como  , donde
, donde 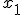 es el número de soldado,
es el número de soldado,  el número de carguero,
el número de carguero,  el de meta-carguero,
el de meta-carguero,  ,
,  el de meta-
el de meta- -meta carguero.
-meta carguero.
Pues resulta que estas malas bestias han creado el ULTRA-meta carguero. Este carguero es un meta-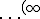 -meta-carguero. ¿Estamos todos condenados? Veamos que no necesariamente. Lo primero es ver cómo se escribe esto formalmente. Hay dos formas:
-meta-carguero. ¿Estamos todos condenados? Veamos que no necesariamente. Lo primero es ver cómo se escribe esto formalmente. Hay dos formas:
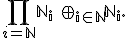
Espera, ¿dos formas distintas? ¿Matemáticos dando nombres distintos a la misma cosa? No me cuadra. Estos conjuntos tienen que ser diferentes, la cosa es ¿en qué se diferencian? Para explicarlo necesitamos ver como es un elemento genérico de cualquiera de estos conjuntos. Para escribirlos necesitamos un vector de infinitas dimensiones, algo del estilo:

Supongamos ahora que nuestros extraterrestres babosos, aparte de un gusto morboso por las matemáticas, lo tienen también por la burocracia. Pero resulta que, como todos los burócratas, son unos gandules de mucho cuidado y decidieron que cada soldado sólo tuviera un número finito de elementos distintos de 0 (para no escribir mucho en el expediente). Es decir, cada soldado tendría un número del estilo:

Que por supuesto abreviaban y solo ponían los términos que eran distintos de 0. Los elementos de este tipo forman el segundo de los conjuntos de antes. A este conjunto se le suele llamar la suma directa o co-producto de conjuntos. Ahora bien, ¿podremos meter todos los soldados del conjunto anterior en una sola nave? Doy una pista y pensad un rato: usa el último truco del que habló Pedro.
Si no das con la respuesta ahí va. Pero primero necesitamos un par de teoremas:
[Pitágoras] Existen infinitos números primos.
La demostración es MUY impactante por lo simple que es. Merece la pena perder 5 minutos en echarle un ojo.
[Pitágoras] Todo número natural se puede descomponer en producto de potencias de números primos de forma ÚNICA.
Vamos a usar estos teoremas para construir una aplicación entre los números naturales y el conjunto suma directa. Cogemos un soldado cualquiera y supongamos que su número es  y supongamos que tenemos una aplicación (que llamaremos
y supongamos que tenemos una aplicación (que llamaremos  ) que asocia cada número natural
) que asocia cada número natural  al primo que hace el número
al primo que hace el número  . Es decir:
. Es decir:

Entonces cogemos a este soldado y lo metemos en el camarote:

Que es un número natural. Está bastante claro que a cada soldado del super ultra meta carguero le asocio UNO Y SÓLO un camarote de un carguero standar. Ahora bien, ¿queda algún camarote libre? Pensad un poco.
La respuesta es que NO, pues cada número natural se puede descomponer como un producto de potencias de números primos (lo vimos antes con el segundo teorema), y por lo tanto le podemos asociar el soldado correspondiente de super-ultra-carguero. Con eso hemos construido una aplicación biyectiva entre el conjunto suma directa y los números naturales. Como conclusión, el super-ultra carguero ¡¡no tiene más soldados que un carguero normal!!
Sobre el otro conjunto, que se llama producto, hablaremos más adelante cuando hayamos hablado de los números reales, pues es una mala bestia que tiene resultados aún más soprendentes.
Ahora el resumen clásico. En esta entrada hablamos sobre la unión, el producto y el co-producto de conjuntos y de las paradojas relacionadas con ellos cuando los conjuntos son infinitos. La moraleja se puede resumir en el siguiente teorema:
1. La unión (incluso de un número infinito numerable) de conjuntos numerables es numerable.
2. La suma directa (incluso de un número infinito numerable) de conjuntos numerables es numerable.
Por cierto, si estás pensando que este tipo de construcciones son muy “raras” piensa que los polinomios son un espacio co-producto. Ejemplos de espacios producto los pondremos en su momento.
En la siguiente entrada hablaremos las relaciones de equivalencia y los conjuntos cocientes, que nos van a facilitar mucho la vida a lo largo de la serie.

The De la Lógica a la Relatividad – Producto y coproducto de espacios. by Cruz Enrique Borges Hernández, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.





{ 6 } Comentarios
Acabo de enlazar aquí desde el artículo del Hotel de Hilbert en El Tamiz: es una excelente ampliación teórica para quienes lean aquello y quieran profundizar más
Por cierto, con 4+1 artículos, creo que esta serie ya tiene la entidad suficiente como para tener su propia página descriptiva/índice. cruzki, si me mandas un correo con una descripción de un par de párrafos, creo la página para que sirva de referencia.
Sin querer ser u incordio: “la aplicación billectiva entre ambos conjuntos.” ¿no debería estar escrito como “la aplicación biyectiva entre ambos conjuntos.”?
No estoy seguro de que cruzki vaya a conectarse hoy o mañana, de modo que lo acabo de corregir yo mismo, ¡gracias!
Me estoy acordando ahora mismo que no pase el corrector ortográfico a la entrada :S :S
Gracias por corregir Pedro y por avisar Fer.
Cruzki, como el buen vino tu serie mejora con el tiempo… ¡Te has superado! Demuestras además unos excelentes reflejos al aprovechar el artículo de Pedro para ambientar y enmarcar el tuyo y, de paso, explicarlo formalmente. Esta serie está muy viva e “interactua” con su entorno. Lo haces fácil y ameno.
Un gallifante para ti.
Los ingenieros también ponemos mucho para denotar una derivada la de Newton, un puntito encima de la función. Sobre todo cuando es una derivada con respecto al tiempo. Y si es segunda o tercera derivada, pues dos puntitos, tres. Es muy elegante
{ 2 } Trackbacks
[...] la próxima entrada hablaremos sobre el producto y coproducto de espacios. http://es.wikipedia.org/wiki/AxiomasdeZermelo-Fraenkel [↩] [...]
[...] Producto y coproducto de espacios (El Cedazo) Comparte esta entrada: El texto de El Gran Hotel de Hilbert , por Pedro Gómez-Esteban, salvo donde se mencione explícitamente, está publicado bajo Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License. Entradas relacionadas: [...]
Escribe un comentario