Tras la breve introducción a la lógica, en esta entrada vamos a empezar a usar el sistema axiomático-deductivo para ir generando objetos que nos permitan llegar a modelar el universo… Sí, parece flipante ¡pero se puede hacer! Antes que nada, el párrafo de advertencia. No soy experto en el tema (de hecho esta parte de las matemáticas es de las que menos se me da, pero bueno) y además pretendo simplificar bastante la materia, así que a partir de ahora es posible que hallan algunas burradas para simplificar. Comenzamos entonces.
Para construir los números naturales vamos a usar el sistema axiomático de Peano[1] que no depende de ningún otro sistema axiomático. Hay otras formas de generar los números naturales, pero nos quedaremos con ésta que, para mí, es la más intuitiva. Los axiomas de Peano dicen (copy-paste de la Wikipedia):
- 1 es un número natural. Es decir, el conjunto de los números naturales es no vacío.
- Si
 es un número natural, entonces
es un número natural, entonces 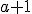 también es un número natural, llamado el sucesor de
también es un número natural, llamado el sucesor de  .
. - 1 no es sucesor de ningún número natural. Es el primer elemento del conjunto.
- Si hay dos números naturales
 y
y  tales que sus sucesores son iguales, entonces
tales que sus sucesores son iguales, entonces  y
y  son números naturales iguales.
son números naturales iguales. - Axioma de inducción: si un conjunto contiene al 1 y a los sucesores de cada uno de sus elementos entonces contiene a todos los números naturales.
Vamos a analizarlos con un poco de detalle.
Para empezar, hay que tener en cuenta que 1 no se refiere al “número uno”. Es sólo una notación de un objeto especial que vamos a llamar 1. Por ejemplo podría ser una patata con forma de ratón muy famoso. El primer axioma simplemente está suponiendo que existe dicho elemento. Esto parece una perogrullada, pero no sería la primera vez que se hacen unos teoremas impresionantes que cuando vas a aplicar resulta que se refieren al conjunto vacío o a la nada.
Con el segundo lo que estamos estableciendo es una suerte de orden. Por decirlo de alguna manera, estamos generando una suerte de “fila india” de patatas mientras que con el tercero lo que estamos diciendo es que la “fila” tiene una cabecera (que es nuestra patata con forma de ratón).
Con el cuarto y el quinto estamos dando condiciones de equivalencia. El cuarto axioma habla de la equivalencia de elementos y el quinto de la equivalencia de conjuntos (recordar que en la entrada anterior explicamos un poco el concepto de equivalencia. A modo de recuerdo / ampliación: dos objetos son equivalentes si son indistinguibles con nuestros axiomas).
Creo que no es muy complicado a partir de los axiomas ver que efectivamente describen lo que intuitivamente consideramos el conjunto de los números naturales. La propiedad principal de los números naturales es que los números están “ordenados” en fila “india” a partir de un número que solemos denotar por 1 y que se extiende hasta el infinito. Ahora bien, partimos del elemento 1, que existe porque sí, según nuestros axiomas. A partir de aquí sabemos que existe el siguiente a 1, que normalmente denotamos por 2 y así sucesivamente hasta el infinito.
También observamos que todos los números se pueden poner en una “fila india”, gracias a los axiomas 2 y 4 ya que, en caso contrario, en algún punto se produciría una “Y”, vamos, un número tendría dos sucesores, y esto estaría prohibido por el axioma 4. También podría darse que un número NO tuviera sucesor, con lo cual llegaríamos a que la “fila” tendría “principio” y “fin” pero esto no es posible por el axioma 2. Luego nuestrso axiomas “describen” bastante bien el concepto que tenemos de números naturales (de hecho el axioma 5 nos dice que son IGUALES a todos los efectos, según nuestro sistema axiomático). A partir de ahora denotaremos a este conjunto por  .
.
Aquí el punto importante es el último axioma el cual hace que las demostraciones por inducción sean válidas. Y ahora es cuando surgen las preguntas: ¿qué es una demostración por inducción y porqué son importantes?
Una demostración por inducción es una forma “fácil” de demostrar una propiedad para un conjunto infinito. Básicamente demuestras la propiedad para el primer elemento del conjunto. Luego demuestras que, suponiendo cierta la propiedad para el primer elemento el sucesor también posee esta propiedad. Usando el quinto axioma concluyes que todos los elementos del conjunto poseen la propiedad. ¿Y esto para que se usa? Pues ya que la mayor parte de los lectores son informáticos supongo que alguna vez os habéis topado con un algoritmo recursivo[2]. ¿A que se le parece? Pero no solo para algoritmos recursivos, hay MUCHAS demostraciones matemáticas que se hacen por inducción.
Bueno, ya tenemos construidos los números naturales, ahora queremos hacer cosas con ellos. Pero para hacer cosas con ellos primero vamos a necesitar un poco de teoría de conjuntos para hablar de aplicaciones entre conjuntos. Y eso mejor lo dejamos para la próxima entrada.
Y para terminar, el resumen habitual.
Hemos supuesto que existe un elemento, hemos dado una suerte de forma de ordenar los elementos y de compararlos y con ello hemos construido los números naturales. En medio hemos tenido que hablar de la inducción.
NOTA: en la entrada hay una pequeña trampa. Un gallifante a quien la descubra.
- http://es.wikipedia.org/wiki/Postulados_de_Peano [↩]
- http://es.wikipedia.org/wiki/Algoritmo_recursivo [↩]

The De la Lógica a la Relatividad: Los números naturales by Cruz Enrique Borges Hernández, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.




{ 36 } Comentarios
A mi hay dos cosas que no me han quedado claras: 1) ¿Por qué la igualdad se tiene que demostrar con la igualdad de sucesores? 2) ¿Por qué se da por supuesto el comportamiento del signo ‘+’? Yo en principio no sabría que significa ‘a + (patata con forma de ratón)’. Por lo demás, una fantástica explicación. Ya estoy aficionado a El Tamiz y a El Cedazo.
Cruzki, enhorabuena por la serie. Este artículo es tan bueno como la observación de Forni, que es igual de tiquismiquis que yo. Estoy deseando de llegar al último capítulo.
@Formi
1) Imagina lo siguiente. Queremos saber si 1 y “patata con forma de ratón” son el mismo número. ¡No podrías! Pero sin embargo sus sucesores son “el mismo número”.
2) Esa es la trampa En principio tendría que haber hablado de la existencia de una aplicación “sucesor de un elemento” y se habría complicado todo un poco así que lo dejé así. Si te sigue chirriando mucho, donde ponga un “+” pon “sucesor de(x)” y ya esta. De todas formas, ten en cuenta que a+”patata” no tiene por que estar mal definida. En este contexto “a” sería (si se ha definido al modo “usual”) un conjunto con “a” patatas y sumarle una es simplemente añadir una patata.
En principio tendría que haber hablado de la existencia de una aplicación “sucesor de un elemento” y se habría complicado todo un poco así que lo dejé así. Si te sigue chirriando mucho, donde ponga un “+” pon “sucesor de(x)” y ya esta. De todas formas, ten en cuenta que a+”patata” no tiene por que estar mal definida. En este contexto “a” sería (si se ha definido al modo “usual”) un conjunto con “a” patatas y sumarle una es simplemente añadir una patata.
Pero si la demostración es con los sucesores, nunca podrías demostrarlo, pues para demostrar que 1=1 debemos ver si 2=2, que lo demostramos si 3=3, que sólo será cierto si 4=4, … ¿No sería mejor enunciar con los predecesores? Si a es un sucesor de b (a=b+1), y c es un sucesor de d (c=d+1), entonces a=c si b=d. Si sigues la serie al final llegarás a 1=1, que es precisamente el primer axioma de la definición. Quiero decir, que por definición el símbolo 1 es “patata con forma de ratón”, y no 1=patata porque 2=patata+1.
Ese es lo que quiere decir, es posible que no se me haya explicadobien :S
Entonces, yo cambiaría: “Si hay dos números naturales a y b tales que sus sucesores son iguales, entonces a y b son números naturales iguales.”. Por: “Si hay dos números naturales a y b tales que SON sucesores DE DOS NÚMEROS NATURALES iguales, entonces a y b son números naturales iguales.”. De todas maneras, seguro que sólo te puedo seguir la serie hasta aquí. ¡¡ Ay cuando lleguen los Reales !!
Y sobre todo… Somos la mayoría de los lectores informáticos de profesión? Porque yo estudio Filología Inglesa, oiga.
jajajaja, parecde que se ha supuesto un axioma erróneo
Una pregunta, porque algunos matematicos incluyen el cero el el conjunto de los naturales??
Es una buena pregunta otanion, yo también me la he hecho. Creo que no está del todo bien resuelta por lo que sé, ya que más de una vez me he encontrado que se incluye a conveniencia.
Todos los lectores No son informáticos, doy fe.
@ otanion
Generalmente es por evitarse problemas al dividir o cosas de ese estilo. En esta entrada es simplemente por la “trampa” que hecho en los axiomas.
@ Pedro
Una encuesta para saber la “profesión” de los lectores no estaría mal sobre todo para saber por donde tengo que buscar ejemplos.
@Forni
He estado pensando en el asunto y creo que no es necesario tocar nada. El truco es usar tu mismo argumento, pero en vez de “hacia atrás”, “hacia delante”. A ver si me explico:
Queremos saber si “a+patata”=”b+zanahoria”. Entonces empezamos a calcular los sucesores de “patata” hasta llegar a “patata+a” y los sucesores de “zanahoria” hasta llegar a “b+zanahoria” de la siguiente forma:
patata=zanahoria => patata+1=zanahoria+1 => patata+2=zanahoria+2 …
Si, por ejemplo, llegamos a:
patata + a = zanahoria + a
con “zanahoria+a != zanahoria+b
ya lo tendrías. Mucho ojo, aquí hay que tomarse a y b “con la trampa”. En realidad estamos aplicando el sucesor de zanahoria “a” veces y el sucesor de zanahoria “b” veces y luego comprobamos si son el mismo elemento.
@ cruzki,
Mi consejo es que intentes poner ejemplos que cualquiera pueda entender. Por lo que sé, hay de todo, y los nuevos lectores no habrían hecho la encuesta… cuanto más genérico, mejor
Con respecto al número 0, en http://es.wikipedia.org/wiki/Postulados_de_Peano dice:
Yo también he estado pensando en el asunto, y también creo que no hay que tocar nada pues estos axiomas llevan largo tiempo escritos y no voy a ser yo precisamente el que vaya a descubrir un error. Luego el error está en mi cabeza, no en la de Peano . He revisado las definiciones de los axiomas en la Wiki, tanto en español como en inglés (creo que la versión inglesa está más completa, sobre todo por los axiomas de ‘igualdad’). El problema viene de mi entendimiento de la lógica aplicada (siempre he tenido problemas con la lógica formal y la estadística, que se le va a hacer). La formulación de Peano original (números naturales distintos tendrán sucesores distintos (a!=b ==> S(a)!=S(b)) me parece más clara de entender: el sucesor de un número natural dado será otro distinto de su predecesor y dado un predecesor sólo podrá tener un sucesor (los números naturales son una serie ordenada de objetos distintos entre si). Pero al darle la vuelta a la implicación tal y como explicaste en la introducción (a=b <== S(a)=S(b)) sigo pensando que es como construir la casa empezando por el tejado (como puse en mi anterior comentario). ¿No quedaría más claro con un ‘si y sólo sí’ en vez de con una implicacióm simple (a=b <==> S(a)=S(b))?
. He revisado las definiciones de los axiomas en la Wiki, tanto en español como en inglés (creo que la versión inglesa está más completa, sobre todo por los axiomas de ‘igualdad’). El problema viene de mi entendimiento de la lógica aplicada (siempre he tenido problemas con la lógica formal y la estadística, que se le va a hacer). La formulación de Peano original (números naturales distintos tendrán sucesores distintos (a!=b ==> S(a)!=S(b)) me parece más clara de entender: el sucesor de un número natural dado será otro distinto de su predecesor y dado un predecesor sólo podrá tener un sucesor (los números naturales son una serie ordenada de objetos distintos entre si). Pero al darle la vuelta a la implicación tal y como explicaste en la introducción (a=b <== S(a)=S(b)) sigo pensando que es como construir la casa empezando por el tejado (como puse en mi anterior comentario). ¿No quedaría más claro con un ‘si y sólo sí’ en vez de con una implicacióm simple (a=b <==> S(a)=S(b))?
Respecto al cero,
en http://en.wikipedia.org/wiki/Natural_numbers se aclara algo más — tradicionalmente no se incluía el 0, pero a partir del siglo XIX se empezó a definir incluyéndolo al utilizar teoría de conjuntos, y actualmente se suele incluir el 0 en el contexto de teoría de conjuntos, informática y lógica matemática, mientras que no suele incluirse en teoría de números.
Pero creo que, habiendo entendido la explicación de cruzki, resulta claro que ambas versiones son igualmente válidas: lo esencial es que es un conjunto ordenado e infinito “por un lado”.
Cruzki, se puede saber que este artículo forma parte de una serie debido a que en el primer párrafo te refieres a la primera entrega. Sin embargo quizás quedaría esto más claro si haces como Pedro o Manuko, que al título del artículo propiamente dicho anteponen el nombre de la serie. Por ejemplo, “Cuántica sin fórmulas – El efecto túnel”.
Por lo demás te animo a seguir divulgando las matemáticas, pues lo estás haciendo muy bien.
@ Mazinger,
Aparte del título (eso lo dejo a elección de cruzki), cuando haya un par de entradas más crearemos una categoría (“colgando” de “cruzki”) para agrupar todos los artículos de la serie, además de una página índice/descripción, para que sea más útil como referencia.
Me parece muy bien… Los seguidores de la serie lo agradeceremos. Aprovecho para decirte que han desaparecido las categorías de la columna izquierda de El Tamiz. No se ven los títulos de las series. O eso o voy a tener que cambiar de gafas.
Pedro, considera retirado mi comentario anterior. Acabo de ver la nueva combobox para seleccionar la categoría.
Sorry.
@Pedro
Ya, el problema es ¿qué es genérico? Sobre todo con la deformación de la realidad que sufre un matemático (no quiero ni pensar la que sufre un filósofo)
(no quiero ni pensar la que sufre un filósofo)
@ Mazinger
Te tocó buscarle un nombre corto a la serie
@ cruzki,
Ah, eso tienes que pensarlo tú mismo Por si te sirve, yo intento imaginarme que se lo estoy contando a alguien de unos doce-quince años de edad, inteligente pero sin muchos conocimientos previos.
Por si te sirve, yo intento imaginarme que se lo estoy contando a alguien de unos doce-quince años de edad, inteligente pero sin muchos conocimientos previos.
¿Buscar un nombre corto? Vaya, ahora entiendo eso de que El Tamiz/El Cedazo te hace pensar.
Te advierto de que quizás no ayude demasiado a tu serie que yo le busque nombre, dado lo negado que soy para el marketing. Inicialmente me decantaría por el sencillo pero descriptivo “Variedades riemannianas”, que si bien no es muy comercial, al menos se ajusta con rigor y exactitud a lo que pretendes (creo): explicar de dónde salen, qué son y para qué sirven las variedades riemannianas.
Ahora bien, si buscáramos enganchar a más lectores a la serie quizás podríamos pensar en un título más llamativo. Para ello podríamos jugar con el hecho de que en el capítulo final aparecerá de forma estelar la mundialmente conocida y admirada Teoría de la Relatividad General. En tal caso podríamos ampliar un poco el título (ya no sería tan corto): “Relatividad y variedades riemannianas” o “Relatividad y Riemann”. De estos dos el último no parece adecuado pues da a entender que se centra en el matemático más que en su obra.
¿Y qué cabe pensar sobre “Relatividad y variedades riemannianas” o “Variedades riemannianas y Relatividad”? ¿Es riguroso? Bueno, quizás no tanto como el que propuse en primer lugar, pero ¿induce a error? No creo o al menos no mucho, pues al final de la serie se estudiará el modo en que se relacionan las variedades riemannianas y la TGR. Demasiado largo, no obstante, parece.
Bueno, ante la duda y puesto que soy muy soso me quedo con “Variedades riemannianas” a secas (tengo poca imaginación, ya lo sé).
¿Qué tal “DE LA LÓGICA A LA RELATIVIDAD”?
Porque se ha empezado la serie sentando las bases con la lógica y se espera culminar la serie con la tan esperada Relativida General.
me gusta la propuesta de joel. Luego la cambio que ahora tengo follón en casa
Joel, ahí le has “dao”. Si me conectara por primera vez a El Cedazo y no tuviese ni idea de lo que va esta serie, nada más ver el título me “metería de patas” a leerla.
Aquí hay otro lector no informático, jejeje.
Buen artículo. Esta serie es interesante. Lector no informatico
Muy buen artículo. Esta serie viene muy bien para aquéllos, como yo, que no tenemos muchos conocimientos de matemáticas y, por el contrario, nos gusta. ENHORABUENA
No se que le pasa a esta página pero lo que yo estoy buscando es los números escritos en ionglés, no estoy filosofando sobre los númeron
@ Olga,
No, si a esta página no le pasa nada
¿La serie está abandonada?
Una pena, me estaba gustando bastante.
En cuanto a lo del número 0, yo sabía que lo habían inventado los musulmanes. Es la razón por la que el siglo XXI empezó en el año 2001 y no en el 2000.
Pero ya tengo la curiosidad: ¿quién inventó los números decimales?¿y los negativos?
Una cosita… En el primer párrafo hay una errata. Entiendo que es “hayan” del verbo haber, no “hallan” del verbo hallar.
En realidad, debería ser “haya”, con i griega, y en singular ya que ha de concordar con el pronombre relativo “que”, que a su vez concuerda con la forma verbal “es”: “(…) es posible que haya alguna burrada (…)”
De acuerdo con AntonioE y añado que igualmente se diría haya con el plural: “(…)es posible que haya algunas burradas”.
Venger, el siglo XXI empezó en 2001 porque el siglo I empezó en el año 1. Entonces contamos 100 años hasta el cien incluído y por tanto el siglo II empieza en el año 101. Así sucesivamente. Creo, y esto es absolutamente personal e irrelevante, que aunque los romanos hubieran conocido el 0, no habrían empezado a contar los años en 0. Otra cosa es qué año fue el 1, porque si contamos a partir del nacimiento de Cristo, que fue el 24 de diciembre… Esto nunca lo he tenido claro. ¿Ese año fue el año 1 y 7 días más tarde fue el año 2? Si no, entonces Cristo nació matemáticamente en el año 0, aunque el 0 no se conociera
Tampoco me hagas mucho caso pero los decimales tengo entendido que los inventó Francisco de Napier, el mismo de los logaritmos neperianos. Hizo un montón de contribuciones extraordinarias a las matemáticas, pero murió pensando que su más relevante e importante obra fue un estudio por el que demostraba que el Papa era el Anticristo. Esto me lo contó un profesor de cálculo que tampoco era un ejemplo de cordura, así que tómalo con pinzas.
Escribe un comentario