Hoy utilizaremos noticias de actualidad para seguir avanzando en nuestra serie de Teoría de juegos: un escándalo de corrupción.[1] Veremos cómo dos partidos políticos se enfrentan a un escándalo de corrupción, y cómo eligen su mejor acción utilizando la teoría de juegos.
Aprovecharemos el juego para presentar un par de conceptos nuevos, maximin y minimax, y veremos cómo los hemos ido usando implícitamente a lo largo de la serie.
La situación es la siguiente: sorprendentemente, un alcalde electo ha sido pillado aceptando sobornos de un contratista (no sé si lo sorprendente es que los haya aceptado o que le hayan pillado; que cada cual elija). El asunto aún no ha sido hecho público, pero tanto el partido en el poder (Partido Naranja o PN) como la oposición (Partido Amarillo o PA) ya lo conocen, y pueden tomar tres opciones:
- Condenar el asunto enérgicamente.
- Quedarse Callados, ni confirman ni desmienten.
- Defender la actuación del alcalde.
Además, las elecciones están muy cerquita, así que la posición que tome cada partido ante dicho asunto puede ser determinante. Nosotros tomaremos el lugar del Partido Naranja.
Lógicamente, cada acción supondrá distintos réditos electorales. El Partido Naranja ha hecho un estudio basado en encuestas a los ciudadanos y en su propia experiencia, y ha llegado a la siguiente matriz de pagos:
| PA | ||||
| Condenar | Callar | Defender | ||
| PN | Condenar | 45 | 40 | 50 |
| Callar | 25 | 50 | 60 | |
| Defender | 50 | 15 | 70 | |
En la matriz ponemos el porcentaje de votos que conseguiría el Partido Naranja en las próximas elecciones, mientras que el Partido Amarillo conseguirá los que falten hasta el 100% (consideramos que las abstenciones, votos en blanco y votos a otros partidos ya han sido eliminados del análisis). Así, si el Partido Naranja obtiene el 40% de los votos, el Partido Amarillo obtendrá el 60% y gobernarán los Amarillos.
Nótese que esta es la matriz de pagos que conoce el Partido Naranja. El Partido Amarillo puede haber hecho otras encuestas distintas y tener otra experiencia, y creer que la matriz de pagos es otra, e incluso puede que la suya sea la correcta. No nos importa: nosotros decidiremos en función de lo que sabemos (o creemos saber) y no haremos suposiciones sobre qué datos manejan ellos.
¿Cuál es la mejor estrategia para el Partido Naranja?
Estrategia maximin
Como casi siempre, es un poco complicado de entender, pero se ve mejor si lo estudiamos sobre nuestro ejemplo.
Si nosotros somos el Partido Naranja, y queremos elegir según una estrategia maximin, debemos empezar suponiendo que ya hemos elegido, y poniéndonos en el peor de los casos para la decisión del contrario.
Así, si nosotros decidimos Condenar, lo peor para nosotros es que el Partido Amarillo elija Callar, de modo que obtengamos el 40% de los votos. Podemos interpretar esto como que si lo Condenamos nosotros, los votantes pensarán que el alcalde era una sola manzana podrida que nosotros mismos estamos denunciando, y no nos castigarán mucho.
Si en el Partido Naranja elegimos Callar, lo peor que nos puede ocurrir es que los Amarillos elijan Condenar, y obtengamos entonces el 25% de los votos. Podemos interpretarlo como que si lo destapan ellos, los votantes nos castigarán mucho.
Finalmente, si los Naranjas elegimos Defender, lo peor es que ellos elijan Callar, y obtengamos el 15% de los votos. Podemos interpretarlo como que el pueblo piensa: excusatio non petita, accusatio manifesta.[2]
Y ahora elegimos la mejor de esas 3 opciones: Condenar. Conseguimos el 40% de los votos y no gobernamos, pero al menos obtenemos unos pocos concejales.
Nótese que no estamos diciendo “si nosotros elegimos Condenar, ellos elegirán Callar“, sino “si nosotros elegimos Condenar, no sabemos qué van a elegir ellos, pero lo peor que nos podría pasar es que eligieran Callar“. No sabemos qué van a elegir en el Partido Amarillo porque no sabemos la matriz de pagos que ellos están manejando. Podría ser que sus encuestas sean peores (o mejores), o que no sean jugadores racionales o cualquier cosa. No nos importa. Estamos suponiendo que no sabemos cómo va a elegir el Partido Amarillo y poniéndonos en el peor de los casos.
Es como si dijéramos “me conformo con ganar poco en vez de arriesgarme a ganar mucho y equivocarme” o “elijo el máximo de los mínimos”. Es por eso que se dice que maximin es una estrategia conservadora.
Por supuesto, la elección de los valores de la matriz no es trivial, y además es importantísima. Puede que nuestros políticos los hayan averiguado en base a encuestas de intención de voto, o a su experiencia o a lo que sea. Si la matriz fuera otra, los mínimos serían otros y el máximo de los mínimos también sería otro. En este caso concreto parece que cuando el Partido Naranja Condena a su propio alcalde lo hace por honor y por respeto a las leyes, cuando en realidad lo hace en base a un despiadado cálculo. Pero no nos centremos en el hecho concreto del ejemplo, sino en el procedimiento. El hecho de que haya salido eso en nuestro ejemplo es pura casualidad, y depende de los números que elijamos para el ejemplo.[3]
Relacionada con la estrategia maximin está la estrategia minimax.
En realidad es lo mismo, pero a veces nos encontramos con problemas para describir las ganancias y nos resulta más fácil describir pérdidas. En ese caso a menudo cambiamos los signos de la matriz de pagos, de forma que ponemos las pérdidas en positivo, y entonces nuestro objetivo no es conseguir cuanto más mejor, sino cuanto menos mejor. Entonces, el lenguaje utilizado cambia y debemos utilizar la palabra minimax. Pero si lo pensamos con cuidado, vemos que el algoritmo es el mismo, y de hecho tengo la impresión de que minimax es más usado como expresión coloquial que maximin.[4]
Maximin en el árbol de decisión
Como veíamos, cuando representábamos el juego en su forma estratégica (en una matriz de pagos), debíamos suponer que nosotros ya habíamos decidido y ponernos en el peor de los casos a partir de ahí. Pero si lo presentamos en forma de árbol esa suposición ya está implícita en el nodo en que nos encontramos. Quizá de esta forma se verá más claro, porque se ve el camino que va tomando la decisión, y además nos permitirá enfatizar el hecho de que no estamos anticipando lo que va a hacer el oponente, solo poniéndonos en el peor de los casos.
Veámoslo con un ejemplo. Supongamos que tenemos un juego que podemos representar con el siguiente árbol (no se me ocurre ningún ejemplo real que cuadre con el árbol que quiero dibujar, así que no lo voy a forzar; supongamos que el árbol es ese, y punto):
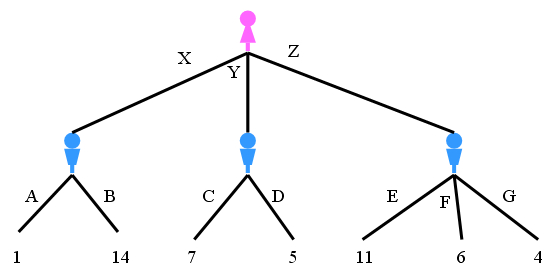
Ana puede decidir X, Y o Z. Para cada una de sus elecciones, Alberto tiene varias elecciones posibles, que llevarán a una determinada recompensa para Ana.
Nótese (y este es el punto que quería enfatizar respecto al escándalo de corrupción de más arriba) que no ponemos en ningún lado la recompensa de Alberto. Si conociéramos la recompensa de Alberto en un punto dado, nos resultaría más sencillo, porque sabemos que Alberto elegirá maximizando su propia recompensa. Pero entonces no estaríamos ante una estrategia maximin, sino simplemente anticipando las decisiones de Alberto, como ya hemos hecho anteriormente a lo largo de la serie. Cuando aplicamos una estrategia maximin, es porque no podemos anticipar las decisiones que tomará el otro, bien sea porque no conocemos sus recompensas (y por lo tanto no sabemos cuál de sus decisiones le favorecerá más a él) o bien sea porque aún conociéndolas no sabemos si el otro se va a comportar de forma racional (egoísta) o irracional o social o malvada, o bien sea porque él cree que sus recompensas serán otras y aun actuando él racionalmente, no sabemos en base a qué matriz de pagos está trabajando.
Debéis perdonarme que haga tanto énfasis en este punto, pero es que muchos de los textos que he leído son ambiguos al respecto y me parece que no siempre queda claro.
Si el juego era de suma cero y de dos jugadores y con información perfecta, como por ejemplo en una partida de ajedrez, el énfasis que ponemos es innecesario (y me parece que por eso otros textos se quedan ambiguos en esto), pero si el juego no es de suma cero, o aun siéndolo es de más de dos jugadores, o si incluso en ese caso la información no es perfecta, podemos conocer nuestras recompensas sin conocer las de los oponentes, y por lo tanto no podemos anticipar sus decisiones.
¿Entendido? Por favor, levantad la mano si alguien no lo ha entendido.
Así que, insistimos, solo nos importan las recompensas para Ana. La idea es ir cogiendo, en cada decisión de Alberto, el caso peor, el que menor recompensa nos proporciona, es decir, A(1), D(5) y G(4), y ahora elegir la que mejor nos resulte: Y (5). Sabemos que en ese caso nuestra recompensa será siempre de al menos 5 (al menos 5, podría ser incluso que fuera 7). Renunciamos a poder obtener el 14, pero al menos sabemos que no obtendremos el 1. Maximin.
Si el árbol tiene una profundidad mayor que dos, también podemos hacer el análisis maximin. Veamos un árbol muy complicado, con varios turnos de decisión y con 3 jugadores: Ana, Alberto y su perro, con quien están jugando a un juego complicadísimo con una pelota. Nos sirve de magnífico ejemplo de cómo alguno de los jugadores puede no ser racional, y aún así podemos aplicar maximin (porque de hecho, el porqué de su decisión no nos importa: nos ponemos en lo peor).
Supongamos que el árbol de decisión en un momento dado es el siguiente:
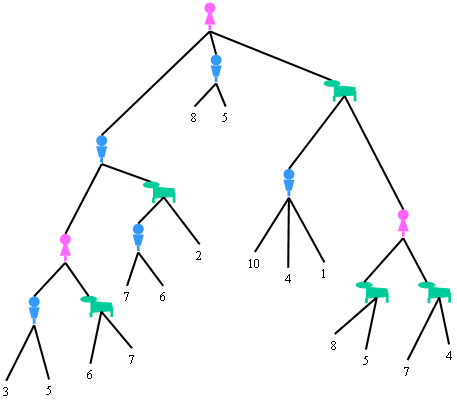
Una vez más, he estado dándole muchas vueltas a cómo podía utilizar un ejemplo real de decisiones que nos llevasen a considerar ese árbol, pero tras mucho pensarlo me ha sido imposible imaginar un juego que llegue a ese árbol. Así que he dejado de intentarlo. Os imagináis que el juego existe y es muy divertido y se puede describir así y punto.
Empezamos resolviendo todas las decisiones que no dependen de Ana poniéndonos en el peor de los casos. No nos importa si es porque el jugador que toma la decisión es irracional, como podría ser el caso del perro, o es que toma su decisión en base a criterios que no conocemos, como podría ser el caso de Alberto. Simplemente nos ponemos en el caso peor y listo.
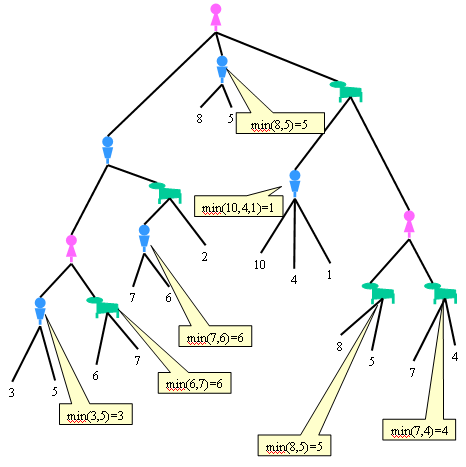
Ahora podemos simplificar todas esas ramas del árbol a ese caso peor:
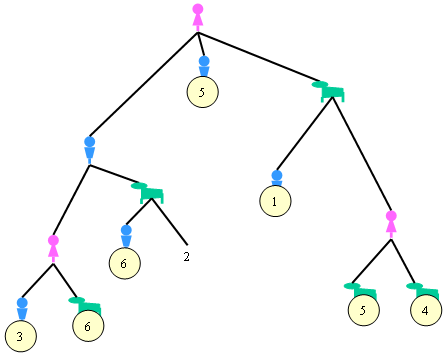
Aún hay una poda más que podemos hacer. Podríamos haberlo hecho en un solo paso, pero así lo vemos todo despacito:
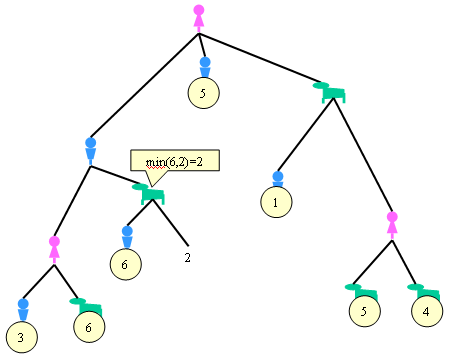

Ahora ya no podemos simplificar más sin hacer que Ana elija. Elegimos el máximo en todas las decisiones de Ana y luego simplificamos el dibujo:
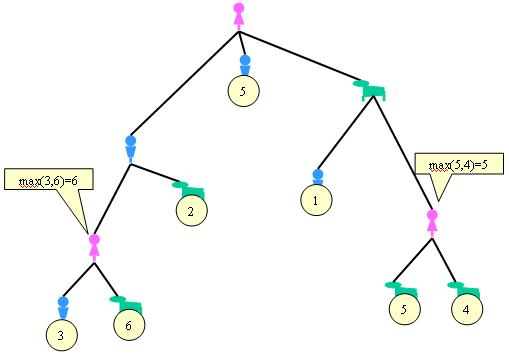
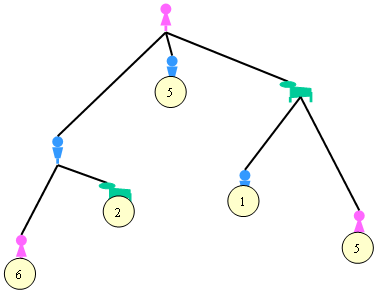
Otra vez estamos en un estado en que todas las decisiones dependen de alguien que no es Ana, así que, una vez más, nos ponemos en el peor de los casos:

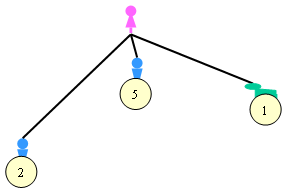
Y finalmente, elegimos el máximo:
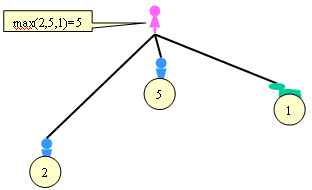
Entonces, ¿tiene Ana que conformarse con ganar 5? ¿No puede intentar ir a por el 10? ¿Es más racional que Ana elija 5 o que intente el 10 aún a riesgo de no conseguirlo? El lector astuto verá aquí palabras como “arriesgarse” o “intentar” que pueden hacernos pensar que introducir la estadística en el análisis podría ayudarnos. Pero eso quedará para el próximo artículo, que este ya está quedando muy largo.
- Desgraciadamente, aunque el momento en que escribo esto y el momento en que se publique pueden estar muy lejanos en el tiempo, seguro que algún nuevo escándalo de corrupción convierte esta frase en verdadera, sea la fecha que sea. Sniff. [↩]
- Escusa no solicitada, acusación patente [↩]
- Mentira cochina. Por supuesto que no es casualidad: he elegido esos números adrede para que salga exactamente eso. [↩]
- Bueno… coloquial en su sentido más amplio. No veo a mi abuela usando coloquialmente la palabra minimax. Pero sí es cierto que muchas disciplinas que estudian poco o nada sobre teoría de juegos utilizan el concepto de minimax. [↩]

The Teoría de juegos XVIII – Escándalo de corrupción by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.





{ 9 } Comentarios
Lo que se aprende aquí, madre de todos los cielos… muchas gracias por el desasne, J. Nosotros, los pobres e inocentes mortales, pensando que los partidos, a veces, son gente honrada, y fíjate tú, que está todo más que sumado, restado, multiplicado y dividido. De todas maneras, me lo tengo que leer otra vez, porque mi intelecto es limitado y hay cosas que se me han quedado un pelín oscuras, pero es tela de interesante.
Y un detalle de latín… la expresión usual es Excusatio non petita, accusatio manifesta, (en vez de la que pones tú explicatio non petita, excusatio manifesta), pero vaya, el espíritu es el mismo: si te disculpas o te explicas demasiado sin que nadie te lo pida, te estás autoacusando de manera flagrante.
¡Sigue así, por favor!
Si es que yo soy de ciencias…
Corregido.
Creo que todos hemos aplicado inconscientemente estrategias de este tipo con esa asignatura que se nos atragantaba. ¿Estudio de todos los temas y voy a por nota o me centro en unos pocos y voy a por al aprobado? Si es que la necesidad saca el ingenio!
Pues esta estrategia la aplica mucha gente a diario sin saberlo cada vez que invierte en depósitos en el banco: ¿me la juego con un depósito a plazo fijo (que sé que nunca pierdo, pero nunca gano mucho) o uno variable que invierte en bolsa (puedo ganar mucho, pero perder mucho también)?
Los conservadores prefieren ganar poco, pero seguro (maximin). Como dije otras veces, esta serie se aplica tan fácil a casos reales que se hace súper interesante.
“Lo que se aprende aquí, madre de todos los cielos…”
Que buen articulo… me felicitas al diseñador gráfico!
Siguiendo el nivel de la serie, ¡Genial la explicación! Yo creo que suelo ser más bien conservador ahora que he entendido un poco mejor el tema, porque me he identificado con algunas explicaciones.
Estimado J, creo que estoy desfasado algunos cuantos años en lo que voy a preguntar, incluso a riesgo de que no he terminado de leer la serie completa pregunto: Si bien la estrategia maximin sugiere elegir la acción que produce la menor perdida, en el problema planteado de corrupción, según la matriz de pago, si el partido naranja elige “condenar”, en 2/3 de los casos perderá la elección y en el 1/3 restante es incierto ya que es 50 y 50, es decir se sugiere una opción que en ningún caso permite ganar la elección. Dado lo anterior, si PN pretende maximizar la probabilidad de ganar, tanto la opción callar como defender garantizan 2/3 de posibilidades de no perder y 1/3 de ganar…. Asumiendo solo 1/3 de riesgo de perder estrepitosamente, pero en 4 o 6 años es seguro que otro escándalo hará que esto quede olvidado y podría no ser gran problema para la próxima eleccion. ¿Te parece lógica esta estrategia o debo catalogarme dentro del grupo de Xuglurz irracional? Ojalá aun respondas comentarios incluso después de tanto tiempo de esta publicación. Un gran saludo
Xuglurz.Cl,
la estrategia maximin es conservadora, depende de lo que quieras conseguir y de tu tolerancia al riesgo, puede ser mejor una cosa o la otra.
Imagina el siguiente caso: eres uno de los candidatos del PN. No el líder, solo uno de los candidatos. Pero tú mismo estás inmerso en tu propio problema legal: si logras ser diputado, se te aplicará el aforamiento y eso por no contar con que contarás con cierta influencia para afectar a tu problemilla legal. Si no lo logras, todo eso lo pierdes y puedes acabar en la cárcel. ¿Te arriesgarás al 70 sabiendo que puede que te quedes en el 15, y por lo tanto no consigas tu escaño? ¿O prefieres ser consevador, conformarte con el 40 (en el peor de los casos) y ser diputado? Tu partido probablemente no ganará y algunos de tus compañeros no conseguirán el escaño, pero al menos te habrás asegurado el puesto unos añitos y probablemente no vayas a la cárcel.
{ 1 } Trackback
[...] de juegos XVIII – Escándalo de corrupción, de Javier “J” Sedano, que pode lerse en El Cedazo. Toda a serie Teoría de juegos está publicada en forma de libro, [...]
Escribe un comentario