En esta entrada continuamos nuestro camino hacia la descripción del universo. Tras hablar un poco de lógica y del conjunto de los números naturales pasamos ahora a hablar de conjuntos y aplicaciones entre conjuntos.
A mi modo de ver, una de las cuestiones más incómodas para fundamentar las matemáticas es definir qué es un conjunto. Todo el mundo sabe qué es un conjunto, pero expresarlo matemáticamente es altamente NO trivial. De hecho no es hasta principios del siglo pasado cuando Zermelo y Fraenkel consiguen una teoría “decente”[1].
No puedo resistirme a hablar un poco más del tema porque quizás os suene de algo. Fue Cantor a finales del siglo XIX el primero que se propuso fundamentar TODA la matemática a partir de una serie de axiomas que es lo que comúnmente denominamos “Teoría de conjuntos”. Copio su definición de conjunto:
Se entiende por conjunto a la agrupación en un todo de objetos bien diferenciados de nuestra intuición o nuestra mente.
El gran problema de esta definición es que admite como conjunto el conjunto de los conjuntos que no se contienen a si mismos… ¿Mande? Veámoslo mejor con un cuento[2]:
En un lejano poblado de un antiguo emirato había un barbero llamado As-Samet diestro en afeitar cabezas y barbas, maestro en escamondar pies y en poner sanguijuelas. Un día el emir se dio cuenta de la falta de barberos en el emirato, y ordenó que los barberos sólo afeitaran a aquellas personas que no pudieran hacerlo por sí mismas. Cierto día el emir llamó a As-Samet para que lo afeitara y él le contó sus angustias: - En mi pueblo soy el único barbero. Si me afeito, entonces puedo afeitarme por mí mismo, por lo tanto no debería de afeitarme el barbero de mi pueblo ¡que soy yo! Pero si por el contrario, no me afeito, entonces algún barbero me debe afeitar ¡pero yo soy el único barbero de allí! El emir pensó que sus pensamientos eran tan profundos, que lo premió con la mano de la más virtuosa de sus hijas. Así, el barbero As-Samet vivió por siempre feliz.
A esto generalmente se le denomina Paradoja de Russell y supuso un mazazo a la teoría de Cantor lo cual, entre otras cosas, lo llevó a la locura[3]. En próximas entradas hablaremos más de este señor.
Continuemos. Ahora que tenemos definido que es un conjunto vamos a intentar definir que es una correspondencia (que van a ser la base para definir luego las temibles funciones). Se podría decir que una correspondencia no es más que una lista de “pares ordenados” de elementos de dos conjuntos. Ahora bien, existe un conjunto de correspondencias MUY especial, es el conjunto de aplicaciones. Una aplicación es una correspondencias que cumplen la siguiente norma:
- A cada elemento del conjunto de salida le corresponde AL MENOS UN elemento del conjunto de llegada.
- A cada elemento del conjunto de salida le corresponde SÓLO UN elemento del conjunto de llegada.
Parecen iguales, pero son distintas. Vamos unos cuantos ejemplos.
Supongamos la siguiente correspondencia entre el conjunto de Libros y el de Escritores de tal forma que a cada libro le asociamos sus escritores. Tendríamos la siguiente lista:
- La Biblia: “montones de personas”.
- Abstracts ICM Madrid 2006: “otro montón”.
- Antropología culturar: Marvin Harris.
- …[4]
Es fácil ver que NO es una aplicación, pues un mismo libro puede tener “más de un escritor”.
Supongamos ahora que hacemos la siguiente correspondencia entre el conjunto de Personas y Libros. Tendíamos algo así:
- Menganito: -
- Fulanito: -
- Isaac Asimov: “montones de libros”.
- …
Es fácil ver también que esta NO es aplicación pues no sólo una persona puede haber escrito más de un libro, sino que hay personas que NO han escrito ningún libro (recordemos, UN Y SÓLO UN).
Dejo como ejercicio buscar alguna correspondencia que sea aplicación usando el conjunto de Libros. Igual que en la entrada anterior, un gallifante para la más original.
Vemos ahora algunas aplicaciones interesantes. Pero antes un poco de notación y nombres raros:
- Los conjuntos se suelen denotar por letras mayúsculas.
- Las aplicaciones por minúsculas o letras griegas, aunque hay excepciones.
- La notación usual para una aplicación es:
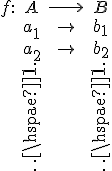
donde 
, 
son cualquier conjunto, 
el nombre de la aplicación y 
los pares ordenados que la forman. Otra forma de escribir los pares es 
.
Supongamos la siguiente aplicación:
Vemos que cumple la definición de aplicación pues todo número natural es par o impar. Ahora bien, también observamos que si “invertimos” las flechas tenemos que es “sólo” una correspondencia pues falla la primera propiedad. A esta correspondencia se la denomina “inversa de una aplicación” y cuando realmente es una aplicación se denomina “aplicación inversa” (que originales los matemáticos, ¿no?), se denota 
(un -1 de superíndice) y se dice que tanto la aplicación original como la aplicación inversa son biyectivas.
Un tipo de aplicaciones importantes son aquellas a las cuales ningún elemento del conjunto de llegada se queda sin ser imagen de otro. El ejemplo anterior es una de ellas. Sin embargo la siguiente no lo es:
pues hay elementos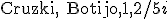 
que no tienen antimagen. O sea, que no hay ningún elemento de partida que los tenga como imagen. A este tipo de aplicaciones se las denomina “aplicaciones sobre” o sobreyectivas y se las puede definir también como aquellas a las cuales su aplicación inversa sólo falla en la propiedad 2.
Otras aplicaciones importantes son las inyectivas que son aquellas en las cuales no hay dos elementos del conjunto de partida que tengan la misma imagen. Observamos, por ejemplo, que la aplicación 
no es inyectiva pues hay muchos números que llegan al elemento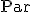 
(de hecho, todos los pares). Sin embargo la aplicación que lleva cada número a si mismo si lo es. Estas tipo de aplicaciones se pueden definir a partir de la aplicación inversa como aquellas aplicaciones cuya inversa es una correspondencia en la que sólo falla la propiedad 1.
Los más avispados seguro que ya os habéis dado cuenta del siguiente teorema.
Una aplicación es biyectiva SI Y SÓLO SI es inyectiva y sobre a la vez.
Las aplicaciones biyectivas serán muy importantes en la próxima entrada pero tener claras estas tres definiciones va a ser FUNDAMENTAL a lo largo de toda la serie, así que si no te ha quedado claro no estaría de más volvieras a leerlo y, si tras leerlo de nuevo tienes dudas, plantéalas en un comentario.
Ahora el clásico resumen:
- Hemos hablado de la definición de conjunto y de sus problemas.
- También hemos hablado de aplicaciones entre conjuntos y algunas de sus propiedades.
En la próxima entrada hablaremos sobre el producto y coproducto de espacios.
- http://es.wikipedia.org/wiki/Axiomas_de_Zermelo-Fraenkel [↩]
- http://es.wikipedia.org/wiki/Paradoja_de_Russell [↩]
- http://es.wikipedia.org/wiki/Georg_Cantor [↩]
- Son los libros que están de alzador de la pantalla del ordenador
[↩]
The De la Lógica a la Relatividad: Aplicaciones entre conjuntos by Cruz Enrique Borges Hernández, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.
{ 12 } Comentarios
Para poder dar una aplicación sobre el conjunto de los libros, primero habría que definir “LIbro”. ¿Qué es un “Libro”? A bote pronto, se me ocurren tres posibilidades:
Posibilidad 1): Un Libro es toda Obra publicada (incluso No Publicada, ¿por qué no?), independientemente de en cuántas ediciones se ha publicado (edición e idioma, diría yo), y de cuál ha sido la tirada de cada edición. Es decir, algo así como “el espíritu del Libro”, que podría ser equivalente al original manuscrito u ordenador-escrito por su autor.
Para esta definición la Aplicación “Medio en que fue escrito por primera vez-Libro” es una aplicación válida: cada libro ha sido escrito por primera vez en uno y sólo un medio (pergamino, papel, ordenador, etc) y en cada uno de estos medios se han escrito muchos libros.
Posibilidad 2: Un Libro es cada edición existente de una Obra literaria (edición-idioma).
La relación Editor-Libro editado es en este caso una aplicación válida: Un libro ha sido editado por un editor particular, que puede haber editado muchos otros libros (incluso ediciones diferentes de la misma obra, que con esta definición sería un “libro” distinto. Para ello, habría que definir editor como aquél que haya editado al menos un libro (si no, sería sólo un “proyecto de editor”).
Posibilidad 3: Un libro es cada copia existente de cada edición existente de una obra literaria.
Con esta definición, la aplicación Número de páginas-Libro sería una aplicación válida: cada libro tiene un determinado número de páginas, mientras que diferentes libros pueden tener el mismo número de páginas. Nuevamente hay que definir que para que un número natural pertenezca al conjunto “Número de páginas de un libro”, debe haber al menos un libro con ese número de páginas; si tomamos el conjunto de los números natural es evidente que no todos los números naturales tienen asociados libros con ese número de páginas, con lo que se fastidia el “al menos uno” de la definición.
Me encanta la lógica.
Y la serie.
@ Macluskey
Le veo problemas a tus razonamientos. Yo no he escrito ningún libro aún pero estoy seguro que NUNCA (actualmente) se escribe un libro por primera vez en un solo medio. Siempre tiras partes de ordenador, partes a mano, en folios, en libretas, etc.
Para la segunda no tengo ninguna pega
Sería una aplicación sobre, pero no inyectiva (hay editores que tienen más de un libro, aunque con tu definición no existe ningún editor no haya editado al menos un libro)
Para la tercera te estas equivocando. Si la aplicación es entre tu definición de libro y los números naturales, de forma que a cada libro lo aplicamos en su número de páginas tendrías una aplicación perfectamente válida. El asunto es que no es sobre (pues esta claro que libros de 10^100 páginas no pueden existir en este universo) y tampoco es inyectiva pues pueden haber dos libros con el mismo número de páginas.
Si cogemos el subconjunto de libros en español podría ser una aplicación biyectiva la que empareje libro y título.
Claro que habrá algún cutre que haya repetido título y estropeará la aplicación que podría haber sido bien bonita xDDDDDD
Podemos intentarlo con el código de barras si sólo tomamos una edición
(¿No crees que podrían ayudar dibujos de conjuntos y flechitas?
)
Cruzki: Me he perdido: Defines aplicación como: “Una aplicación es una correspondencia que cumple la siguiente norma:
-A cada elemento del conjunto de salida le corresponde AL MENOS UN elemento del conjunto de llegada.
-A cada elemento del conjunto de salida le corresponde SÓLO UN elemento del conjunto de llegada.”
Justo después dices que: “Dejo como ejercicio buscar alguna correspondencia que sea aplicación usando el conjunto de Libros. Igual que en la entrada anterior, un gallifante para la más original”
O sea, ¿no me he ganado el gallifante?
Yo no he definido aplicaciones ni inyectivas ni sobreyectivas ni biyectivas. He intentado definir “Aplicaciones-a-secas” tal y como las has definido. Y me sigue pareciendo que son correctas.
En el caso uno, efectivamente un libro puede ser escrito en sesenta soportes diferentes, pero el original definitivo, el que se entrega al editor para su publicación, estará en uno y solo un medio: papel (manuscrito o impreso), manuscrito, digital. Si no es así (o sea, le mando a mi editor la mitad en un email, la otra mitad en papel de servilleta, la otra mitad en papel impreso (sí, ya lo sé, es que escribo libros con tres mitades, ¿qué pasa?), entonces alguien tendrá que hacer la labor de ordenarlo todo para dar origen al original que luego va a editarse. Pero en fin, te doy la razón, quizá sea un ejemplo un poco sacado por los pelos.
Pero en el tercer caso, no estoy de acuerdo. Dado el conjunto “Número de páginas de un libro”, compuesto por todos aquellos números naturales que representen el número de páginas que tiene algún libro editado en el mundo mundial, resulta que cada libro tiene uno y sólo un número de páginas (que existirá en el conjunto “Número de páginas” por definición de ese conjunto), y cada elemento del conjunto “Número de páginas” tiene al menos un libro con ese número de páginas (si no, ese número no estaría en el dichoso conjunto), y quizá muchos.
Es lo que en Informática de Dinosaurio llamamos “Relación 1:n”, o mejor Relacion “1-1:1-n”, que por cierto, son bastante poco comunes, salvo las resultantes de normalizar multivaluadas. Las normales son las “1-1:0-n” (y perdón por los palabros: deformación profesional).
La verdad es que los ejemplos con libros son siempre muy complicados. Si hubieras hecho un ejemplo con facturas y líneas de factura, o cuentas corrientes y movimientos de cuenta, o ya puestos, galaxias y estrellas, la cosa hubiera sido mucho más sencilla.
Aplicaciones biyectivas con libros son difíciles de encontrar. Una aplicación biyectiva es “cliente español particular de un banco”-”DNI”. En estos tiempos, cada persona (física, y susceptible de abrir una cuenta en un banco) tiene un único DNI, y cada DNI está asignado a una única persona. Cuando se implantó el CIF (la letrita del DNI, para entendernos), a finales de los 80, había algunos miles de duplicados en toda España, pero con el tiempo se han ido asignando nuevos DNIs y ya no quedan duplicados (al menos, no deberían quedar, quién sabe).
Un placer.
@Macluskey
Vale, no había que encontrar aplicaciones biyectivas
(joe que me estoy liando con las de la siguiente entrada ¿que pasa?
De todas formas, mucho cuidado con el DNI. A nivel práctico puedes suponer que es único, pero yo no lo programaría sin un try y una excepción como la copa de un pino no valla a ser que la liemos, que conozco a una chica que tuvo que cambiar el número del dni porque estaba duplicado (se dieron cuenta al sacar el carnet de conducir, que no se lo podían dar porque ya había uno con ese dni) al Y estoy seguro que hay más de un español con más de un dni (no dos personas con el mismo, sino una persona con más de un número) aunque supongo que con ese tipo de personas uno no se encuentra por la calle de normal
@naeros
Si tu los haces
… Es que geli ha dejado el listón muy alto.
@Pedro
¿La imágenes las subimos a nuestro propio espacio web o hay forma de subirlas a elcedazo?
@ cruzki,
Estoy con Naeros que, para conjuntos, los dibujitos ayudan mucho (ay, me estoy acordando de los diagramas de Venn del cole). La pobre Gelita no tiene tiempo para ponerse a hacerlos, pero si has visto los banners de Naeros para El Cedazo, puedes estar seguro de que haría un buen trabajo
Puedes subir las imágenes al servidor desde el editor, con “añadir medios – imagen”, lo sube desde tu ordenador y lo enlaza en el artículo.
Por cierto, buen artículo
Vale, perdonado. ¡Faltaría más!
A modo de curiosidad, en estos momentos a los DNIs no les queda más remedio que ser únicos… o el pobre que tuviera un DNI duplicado las pasaría canutas. Lo digo por experiencia. Todas las empresas que yo conozco (gordas, grandes, pequeñas y enormes) asumen DNI===Persona.
Los duplicados vienen del tiempo en que los DNIs se hacían en cada Comisaría de Policía, escritos a máquina, tachando números de una lista que les mandaban de la DGS (sí, “DGS” de Dirección General de Seguridad, en el Edificio de la Puerta del Sol de Madrid que ahora es el de la Comunidad de Ídem: ahora os meteréis conmigo por vejete, y tendréis razón…). Por mucho que los esforzados policías (en aquél tiempo, “grises”) intentaban hacerlo bien, era poco menos que imposible no cometer errores de vez en cuando.
Cuando a fines de los 80 (el 87 u 88, creo), Interior decidió arreglar el asunto, añadió una letra al númerito mediante cierto algoritmo (algoritmo que no fue públicamente conocido hasta varios años más tarde). La Ley decía que, en caso de NIF duplicado, simplemente se configuraba el NIF como el DNI con OTRA letra!!!. Imaginaos la tostada. En estos tiempos, en que todo el mundo conoce el dichoso algoritmo, todos los programas de introducción de datos validan que la letra sea correcta, y si no lo es, no cuela. Mirar el PADRE, por ejemplo, y eso que es de Hacienda. Si la letra no está bien, no hay forma de seguir.
Así que si eres uno de los pocos que pudieran tener un DNI duplicado, más vale que vayas a no-sé-dónde para que te lo cambien, porque si no… En cualquier caso, por motivos profesionales tuve la oportunidad de buscar duplicados en NIFs de una base de datos de centenares de miles de personas físicas (no diré de qué), donde el DNI no era clave de nada (lo era el “Código de Persona”), y por tanto podía estar perfectamente duplicado, Y NO HABÍA NI UNO SOLO DUPLICADO. Es una muestra muy grande, así que creo que no debe haber prácticamente ninguno en toda España.
Ya me callo, que esto tiene poco que ver con los conjuntos y Pedro y/o Cruzki me van a reñir (con razón) y llamarme cascarrabias (sin ella, je, je).
Saludos
@Macluskey
Pos que potra tengo, porque ya te digo, una compañera fue a sacarse el carnet de conducir hace un par de años y no se lo pudieron dar hasta un par de semanas depués de aprobar por eso, porque tenía el dni “duplicado” XD
@Pedro
¿qué usa geli para hacer los dibujos? es que pensaba hacerlos con latex a lo bestia, pero es un rollo que te cagas y con “$programa de diseño vectorial” no queda igual
Por cierto Pedro, si hago diagramas NO SERÍAN DE VEN y te explico porqué (de hecho yo pensaba que lo eran hasta que escribí la entrada
) Tecnicamente los diagramas de Venn son representaciones de como se intersecan conjuntos, nada más o por lo menos eso es lo que dice la wikipedia al respecto.
@ cruzki,
Suele utilizar Gimp e Inkscape más que ninguna otra cosa.
Lo de los diagramas de Venn no era diciendo que los usases, simplemente recordaba con cariño aquellos diagramitas del cole… utiliza lo que corresponda
Yo utilizo el fotochó
Este mes voy a andar bastante ocupado entre exámenes y comenzar el proyecto, así que no sé qué huecos sacaré para terminar la entrada que tengo en borradores y para echarte una mano con los gráficos.
Si quieres mándame un email con lo que quieres que haga exactamente y voy empezando 
Yo estoy ahora super saturado y el poco tiempo libre lo uso para comentar comentar y distraerme un rato. Pensaba escribir los fines de semana pero estoy liado. A ver si saco algo de tiempo para terminar el borrador que tengo y hacer los dibujitos.
Nos vemos
Buen artículo Cruzki, me gusta mucho la serie. Pero tengo algunas dudas, haber si me a quedado todo claro:
Ejemplo 1: Es una aplicación porque: (A=B) es cierto -Es biyectiva e inversa porque: (A=B) y (B=A) es cierto
Ejemplo 2: Es una aplicación porque: (1=impar) es cierto -No es biyectiva ni inversa porque: (1=impar) es cierto pero (impar=1) es falso.
Ejemplo 3: No es una aplicación porque: nada del conjunto es igual a Cruzki.
Escribe un comentario