El Cedazo

Ya hemos visto dentro de esta serie sobre Lógica cómo es un álgebra booleana, cómo representamos funciones en ese álgebra, y su Forma Normal Disyuntiva… Hoy vamos a dejar que suba J a la tarima para contarnos una cosa llamada “reducción de Karnaugh“.

La reducción de Karnaugh es un método poco formal, pero muy ingenieril y astucioso, de buscar la manera de usar los mínimos términos posibles para definir una función lógica, y que además esos términos tengan los mínimos componentes posibles.

Para ello, empecemos por un ejemplo: supongamos que tenemos una función lógica F con dos entradas A y B; y que su definición, en Forma Normal Disyuntiva, es:

F= AB’ + A’B + A’B’

Pensando un poco podríamos llegar a darnos cuenta de que esa fórmula es bastante complicada, y que podríamos simplificarla a

F=A’+B’

¿Estáis de acuerdo en que son la misma función? Haced las tablas de estados de ambas funciones y veréis que es la misma.^[1]

…

¿Ya habéis vuelto?

¿Habéis necesitado hacer las tablas para verificar que son la misma función?

¿O quizá habéis utilizado el método algebraico para generar la FND de ambas funciones y comprobar que son la misma? En el fondo, ambas cosas son lo mismo.

Pero… ¿no parece que la FND es una cosa muy engorrosa? ¿No parece que tiene demasiados términos? Está bien, nos confirma que ambas funciones son la misma, pero además de eso a mí me gustaría que, si me dieran la primera función, fuera capaz de llegar a la segunda con facilidad, ¿no?

Y eso que esta función solo tiene dos variables… imaginaos que tuviera más.

Pues eso es lo que intenta el método de Karnaugh: encontrar una forma simplificada de una función dada.

Para ello nos aprovecharemos de que el cerebro humano es muy bueno reconociendo patrones visuales. No tengo nada claro que pueda contar el procedimiento de manera muy formal, porque además estoy hablando sobre todo de memoria (tiré todos mis apuntes en los que aprendí esto)… pero vaya, es como me lo contaron a mí.^[2]

El problema es que para reconocer esos patrones visuales, tenemos que dibujar, y a día de hoy solo somos capaces de dibujar en 2D en un papel. Eso limita mucho la cantidad de variables que podemos manejar. A mí me resulta difícil hacer mapas de Karnaugh que tengan más de 4 variables, y cuando intento hacerlos de 5 ó más variables, ya empiezo a pensar en el programa que podría hacerlo. Así que voy a contaros el ejemplo de 4 variables, que es el más complejo que podemos pintar con facilidad.

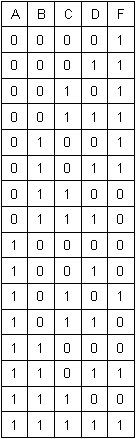
Vamos a suponer una función de 4 variables, que hemos representado según una tabla. Las columnas A, B, C y D son obviamente las 4 variables y F es el resultado de la función.

Lo primero que debemos hacer es conocer el concepto de código circular de Gray. ¿Qué es eso? En un código de Gray tenemos que hacer que entre dos cualesquiera valores consecutivos la única diferencia sea una de las variables.

Jo, qué difícil. Cuando a mí me lo contaron lo hicieron aprovechando los conceptos de bit y código binario, que ya conocía, así que contároslo sin recurrir a ello se me hace complicado… en fin, probemos con un ejemplo.

Si tenemos 2 variables, solemos ordenarlas así:

0 0

0 1

1 0

1 1

Entre la primera fila y la segunda, solo cambia un valor: el segundo 0 se ha convertido en un 1.

Pero entre la segunda fila y la tercera cambian dos valores: el 0 se ha convertido en un 1, y el 1 se ha convertido en un 0.

Peor aún: hemos dicho circular… es decir, que cuando llegamos al final, volvemos a empezar. Es decir, también tenemos que mirar que tras la fila 4ª viene la fila 1ª. En este caso, los dos 0s se han convertido en sendos 1s.

No podemos decir que eso siga el código de Gray…

El código de Gray de 2 variables es el siguiente:

0 0

0 1

1 1

1 0

Fijaos que ahora sí que solo hay un cambio entre la fila 2ª y 3ª, y lo mismo entre la fila 4ª y 1ª y entre todas las demás filas consecutivas.

En este momento, a las personas que saben binario y cómo se codifican los números decimales en notación binaria (que probablemente son todos nuestros lectores, porque hoy en día esto se enseña en el colegio),^[3] se les revuelven las tripas, porque parece como si estuviéramos desordenando los números… pues no. Destierra esa idea de tu cabeza, no traduzcas esos números binarios a decimal. Solo estamos describiendo el comportamiento de nuestra función ante distintas entradas… ¿qué más da que primero escribamos una fila o la otra? Lo importante es que las escribamos todas.

Podríamos generalizar esta idea para 3 ó 4 bits, pero en realidad no nos hace falta para nuestro mapa de Karnaugh. Consultar la página de la Wikipedia si lo necesitáis algún día.

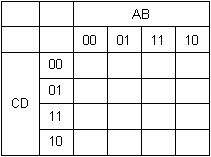
Vale, pues ahora dibujamos una matriz bidimensional, donde en cada eje pongamos 4 valores, ordenados según el código de Gray:

Como tenemos 4 variables de entrada, ponemos 2 variables en filas y 2 en columnas, es decir, 4 filas y 4 columnas. Si tuviéramos 3 variables, podríamos solo 2 filas, por ejemplo. Y si tuviéramos solo 2 variables, podríamos solo 1 fila y 1 columna.

Esta tabla se llama mapa de Karnaugh y es el corazón del método.

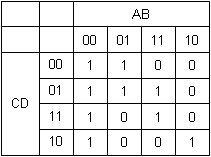
Ahora trasladamos los valores desde nuestra tabla de estado de la función a nuestro mapa de Karnaugh, pero con cuidado de darnos cuenta de que las filas y columnas están ordenadas de una forma “rara”:

Hasta aquí, fácil.

Ahora es cuando viene el arte: hay que buscar los grupos que tengan 16, 8, 4, 2 y 1 unos juntos en un rectángulo (no valen formas raras: tienen que ser rectángulos). Empezamos buscando grupos de 16 unos todos juntos. Obviamente, no tenemos ninguno, porque entonces tendríamos una función que siempre tiene unos… vaya tontería de función… pero bueno, teóricamente sí es posible.

Como no hay, buscamos grupos de 8 unos juntos. Tampoco tenemos ninguno.

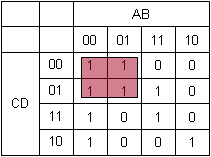
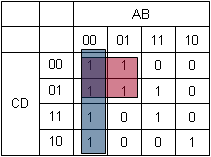
Buscamos entonces los grupos de 4 unos juntos. Yo veo uno muy obvio.

Existe otro más, que se solapa parcialmente con el grupo anterior. No hay problema en que solapen, lo marcamos también.

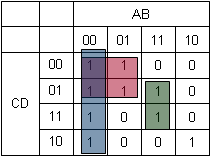
Ya no hay más grupos de 4 unos juntos, así que empezamos a buscar los grupos de 2 unos juntos. Encontramos un grupo y lo marcamos.

No es necesario marcar los grupos de 2 que formen parte completamente de los grupos de 4 que hayamos marcado antes (como por ejemplo, coger de 2 en 2 los que ya tenemos en el azul), pero sí los que se solapen parcialmente, si los hay. También debemos tener cuidado de no crear más grupos de los necesarios, pues existen situaciones en que por ejemplo dos grupos astutamente elegidos serían suficiente, pero si nos confundimos podríamos necesitar 3 (no sé si existe un algoritmo óptimo que encuentre los grupos y te garantice que son como deben ser… yo siempre lo he hecho a ojo; al fin y al cabo con 16 celdas tampoco es tan difícil).

Luego ya no hay más grupos de 2 unos…

…

¿Seguro?

…

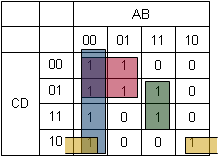
Pues sí, hay otro. Al haber usado un código circular de Gray, lo que “sale” por la derecha, “entra” por la izquierda.^[4] Por lo tanto, existe un grupo más, que marcamos en amarillo:

Obviamente, lo mismo ocurre entre arriba y abajo (lo que “sale” por abajo, “entra” por arriba). Además, podría habernos ocurrido esto mucho antes de haber llegado a los grupos de 2, por ejemplo cuando buscábamos grupos de 4 ó de 8. Este ejemplo lo hemos elegido cuidadosamente para ir mostrando las cosas poco a poco, pero en cualquiera de nuestras búsquedas debemos tener esto en cuenta.

Bueno, finalmente debemos marcar los unos que queden sueltos… son grupos de 1 elemento. Un grupo de 1 uno es muy triste, pero también tiene derecho, el pobre.

Bien, pues cada uno de esos grupos será un término en nuestra función simplificada. En nuestro ejemplo, tenemos 4 términos.

Para construir cada uno de los términos debemos fijarnos en las únicas variables que sean fijas en todo el grupo.

Por ejemplo, para el grupo azul vemos que A siempre vale 0 y B siempre vale 0, mientras que C y D recorren todo el espectro de posibles valores. Así que tenemos que para el grupo azul solo es importante que A=0 y B=0. Sabemos cuál es la fórmula de eso: A’B’. Debemos darnos cuenta de que podemos hacer esto porque hemos ordenado las filas y columnas según un código de Gray, donde un elemento y el siguiente se diferencian solo en uno de los valores… ahora entiendes por qué lo hacíamos, ¿verdad?

Deduciendo de la misma forma encontramos que el grupo rojo es A’C', porque solo B y D barren todos los valores posibles. Los grupos verde y amarillo, como son de solo 2 elementos, necesitan 3 variables, pero podemos deducir del mismo modo que son ABD y B’CD’ respectivamente.

Así que nuestra fórmula completa es:

F=A’B’ + A’C’ + ABD + B’CD’

Podemos entender este método de Karnaugh como lo contrario a la FND. La FND pretendía tener todas la variables en cada término, mientras que este método pretende tener el mínimo posible. Más adelante en la serie veremos que estas dos aproximaciones tienen su utilidad en el mundo real.

Si hubiéramos querido hacerlo para 5 ó 6 variables, tendríamos que haberle dado “profundidad” a la matriz, una tercera dimensión. Pero como no podemos pintar en 3D, se suele poner una segunda matriz a la derecha (para el caso de 5 variables) y otras dos más debajo (para el caso de 6 variables)… pero en esos casos ya es complicado buscar los patrones visualmente. El procedimiento es el mismo, solo hace falta ser capaz de buscar los patrones saltando de matriz en matriz.

Finalmente, podemos pensar un poco y darnos cuenta de que si en vez de agrupar los unos, agrupamos los ceros, podemos construir una suma para cada uno de los grupos y luego multiplicarlos todos, y así llegamos a la fórmula equivalente donde, en vez de tener sumas de productos, tenemos productos de sumas. Como todo en el álgebra de Boole, es dual.

Y hasta aquí el método de Karnaugh de reducción de funciones. El próximo día seguirá la serie exprimiendo los amarillentos apuntes de Macluskey sobre Eso que llamamos Lógica.

 

1. Nota: Esta función es, por cierto, el resultado de hallar la Forma Normal Conjuntiva de la función original, pero es casualidad. [↩]
2. Está bien… confieso que antes de escribirlo he mirado la Wikipedia. [↩]
3. A Macluskey le costó hacer una carrera para enterarse. [↩]
4. Técnicamente se dice que tiene topología de toro o de toroide. [↩]