Seguimos con esta serie sobre los modelos atómicos, aunque aún no hayamos hablado de nada que se parezca a ningún modelo atómico… Pero bueno, nos vamos acercando (recordemos que esta serie no es más que una excusa para hablar de fenómenos físicos sin ninguna relación aparente). Después de ver las colisiones elásticas y ver por encima el Movimiento Armónico Simple, hoy vamos a hablar sobre la Ley de Coulomb y un poco sobre campos eléctricos.
Antes de leer este artículo puede que vaya bien repasar el siguiente: http://eltamiz.com/2009/10/20/electricidad-i-ley-de-coulomb/
4. Ley de Coulomb
Empecemos por lo más básico de todo: ¿qué dice la ley de Coulomb?
La ley de Coulomb puede enunciarse de la siguiente manera:
La fuerza ejercida por una carga eléctrica puntual sobre otra está dirigida a lo largo de la línea que las une. Es repulsiva si las cargas tienen el mismo signo y atractiva si las cargas tienen signos opuestos. La fuerza varía inversamente con el cuadrado de la distancia que separa las cargas y es proporcional al producto de las mismas.
La fuerza que describe la ley de Coulomb es la llamada Fuerza Eléctrica y es inevitable notar que tiene similitudes con la fuerza gravitatoria, pues las dos fuerzas son centrales (es decir, la fuerza que ejerce una partícula sobre otra está dirigida a lo largo de la línea que las une), las dos fuerzas varían inversamente con el cuadrado de la distancia que separa las partículas y son proporcionales al producto de cierta magnitud (la carga eléctrica en la fuerza eléctrica, la masa gravitatoria en la fuerza gravitatoria).
Vamos a introducir también un principio físico que puede que muchos ya conozcáis, el principio de superposición. ¿Qué nos dice este principio? La fuerza ejercida por n cargas sobre una carga Q es la suma vectorial de todas las fuerzas individuales (es decir la fuerza que ejerce la carga Q1 sobre Q, más la fuerza que ejerce Q2, Q3… etc.). Este principio sorprendió algunos físicos de la época, lo que, junto al concepto de acción a distancia, provocó bastantes problemas conceptuales.
El concepto de acción a distancia ha ocasionado muchos dolores de cabeza a los físicos desde siempre, ya que es un concepto bastante anti intuitivo… Pensadlo: solamente por el hecho de que existe una carga provoca una fuerza sobre otra carga… aunque las dos nunca hayan estado en contacto. Aunque entre las dos pueda haber un muro de hormigón, o el vacío, la fuerza es la misma… No cambia, aunque entre las dos cargas haya otra carga o cien cargas, la fuerza de nuevo es la misma…
Para intentar explicar todos estos fenómenos se propuso la Teoría de Campos Clásica (TCC). Según esta teoría, una carga, por el simple hecho de existir, modifica todo el universo creando lo que llamamos un campo eléctrico. Este campo que llena todo el espacio es el que ejerce la fuerza sobre otras cargas.
A partir de esta teoría aparecen muchos conceptos que son muy interesantes, por ejemplo, el concepto de Intensidad del campo en un punto (o simplemente, el campo en un punto), definida como la fuerza que ejercería el campo en un punto P si hubiese una carga de +1C (1 culombio, la unidad de carga). Así la fuerza que crea una carga Q sobre otra carga q0 es el campo eléctrico que genera Q multiplicado por la carga q0. Además, podemos generalizar el principio de superposición de fuerzas y decir que el campo eléctrico generado por n cargas en un mismo punto P es la suma vectorial (ya que la intensidad del campo eléctrico es una magnitud vectorial por definición) de los campos creados por cada carga en el punto P.
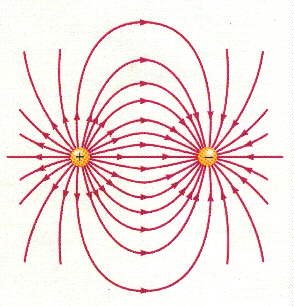
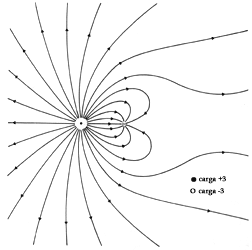
Otro concepto interesante es el de líneas de campo.[1] Éstas son unas líneas imaginarias que nos indican la dirección y el sentido del campo eléctrico en cualquier punto.
Como consecuencia de que la fuerza sea repulsiva entre cargas del mismo signo y atractiva entre cargas de signos opuestos, las líneas de campo “nacen” en las cargas positivas y “mueren” en las cargas negativas. Como el campo eléctrico existe en todos los puntos, dibujar todas las líneas de campo no es una buena idea… por esto las líneas se dibujan simétricamente saliendo o entrando de las cargas, y de tal manera que la densidad de líneas nos indique la intensidad del campo eléctrico en una cierta región y de forma que el número de líneas que entra/sale de una carga sea proporcional a la misma. También es interesante darse cuenta de que cuando la distancia es muy grande, si se dibujan bien las líneas, éstas están igualmente esparcidas y son radiales con respecto a la carga que produce el campo. Además, dos líneas de campo no pueden cortarse en ningún punto, ya que la fuerza que ejerce el campo eléctrico no puede tener dos direcciones distintas.
No vamos a ampliar mucho, porque los conceptos básicos y necesarios de la ley de Coulomb son estos, y seguiremos con conceptos de la teoría de campos en el siguiente artículo.
Si has llegado hasta aquí, en este artículo recomiendo que leas la segunda parte, ya que las ecuaciones que aparecen a continuación no son muy complicadas y ayudan a entender todos los conceptos.
Ley de Coulomb (con ecuaciones)
Esta segunda parte será bastante corta, ya que simplemente es poner ecuaciones a lo dicho en la primera, y no creo que añada nada nuevo…
Bien, primero de todo, ya hemos visto que dice la ley de Coulomb en la primera parte, vamos a traducirla a lenguaje matemático:
“La fuerza varía inversamente con el cuadrado de la distancia que separa las cargas y es proporcional al producto de las mismas.”
Donde K es una constante llamada constante de Coulomb; las dos líneas representan el valor absoluto, es decir que no nos importa si las cargas son negativas o positivas, sólo su valor numérico[2] y ε0 es la permitividad eléctrica del vacío, que vale 8,85·10-12C2N-1m-2, y por consiguiente K=8,99·109Nm2C-2.[3] Con esta ecuación podemos calcular el módulo de la fuerza de Coulomb.
Como la fuerza eléctrica es una fuerza central tenemos que:
Donde F1,2 es la fuerza que ejerce la carga 1 sobre la carga 2 y r1,2 es el vector que apunta desde la carga 1 a la carga 2 (como siempre, la negrita indica vector y sin negrita indica módulo del vector), además, a partir de ahora, un vector con un acento circunflejo será una abreviatura de dividir un vector por su módulo. A esto se le llama vector unitario, ya que es un vector que tiene la misma dirección y el mismo sentido que el original, pero tiene módulo 1. Fijémonos que el vector unitario es muy útil, ya que no afecta al módulo de la fuerza (fijémonos que es la misma expresión que antes), pero nos indica su dirección, que como hemos dicho es la línea que une las dos cargas. Finalmente, nos interesa que la fuerza sea repulsiva cuando las cargas sean del mismo signo y atractiva cuando sean de signos distintos.
Notamos que si q1 i q2 son ambas positivas o negativas la fuerza que ejerce 1 sobre 2 tendrá el sentido del vector r1,2 y por tanto será repulsiva, mientras que, si una es positiva y la otra negativa la fuerza tiene sentido contrario a r1,2 y la por tanto es atractiva.
IMPORTANTE: Quiero hablar de una cosa antes de seguir con el artículo, algo que es muy importante: ¿Qué significan realmente los signos?
A todos, de pequeños, nos enseñan en clase de matemáticas, primero de todo, qué son los números, nos enseñan el número 1, el 2, 3, 4… luego nos enseñan el 0, nos enseñan a sumar y restar números. Cuando ya controlamos todo esto nos enseñan que aparte de todo esto existen más números, que llamamos números negativos, y que son el número -1, -2, -3… Hasta aquí todo bien. Pero ¿qué son realmente los números negativos en matemáticas? No son más que números que cumplen cierta condición. Cada número (a) nos interesa que tenga lo que llamamos “opuesto”, es decir, un número (a’) que cumpla que a+a’=0. Este opuesto en lugar de a’ se escribe por convención -a, y lo que nos indica este número no es más que el hecho que la suma de a con este número es 0. A partir de aquí aparecen los números positivos y negativos, fantástico. Y ¿qué tiene que ver esto con la ley de Coulomb?, os preguntaréis… Pues nada, y esto es lo que quiero que entendáis. Los números negativos no tienen nada que ver con este artículo. Si habéis leído el artículo de Pedro os fijaréis que no habla de cargas positivas y negativas, sino que habla de cargas verdes y rojas. Bien, pues yo hablo de cargas positivas y negativas porque así es como se llaman las cargas por convención. Pero una carga positiva no tiene nada que ver con un número positivo, y una carga negativa no tiene nada que ver con un número negativo. Simplemente, por convención, se otorga un número positivo al valor de una carga positiva y un número negativo al valor de una carga negativa, igual como Pedro, si sigue algún día con la serie de electricidad, supongo que otorgará un número positivo al valor de una carga verde y un número negativo al valor de una carga roja. Todo esto nos sirve porque las matemáticas son una herramienta muy útil para calcular el valor de la fuerza de Coulomb. Pero no la única, pues podríamos calcular el valor de la fuerza de Coulomb de otra forma en que no fuera necesario el uso de números positivos ni negativos. La fuerza de Coulomb la podemos calcular simplemente calculando el módulo de la fuerza y luego, por convenio, decimos que si las cargas son del mismo tipo, la fuerza es repulsiva y si son de tipos distintos es atractiva. Pero como por convención[4] un vector que va en el mismo sentido que otro se dice que va en sentido positivo y si va en sentido contrario se dice que va en sentido negativo, podemos decir que dos cargas del mismo signo producen una fuerza positiva y dos cargas de signos contrarios producen una fuerza negativa. Así que, matemáticamente, podemos tratar las cargas positivas y negativas como números positivos y negativos, llegando al mismo resultado, pero, repito, que podamos hacer esto para simplificar las cosas, no significa que una carga positiva sea lo mismo que un número positivo. Espero que quede más o menos claro lo que he querido decir.
Después de este largo paréntesis, sigamos:
En la primera parte del artículo hemos visto también el principio de superposición de fuerzas, que enunciado matemáticamente viene a ser algo así:
Ésta es la expresión para calcular la fuerza que ejercen n cargas puntuales. Si lo que queremos es calcular la fuerza que ejerce un cuerpo debemos suponer que está formado por infinitas cargas infinitamente pequeñas, llamadas dq, y hacer la suma de todas ellas matemáticamente se escribe:
Donde esta especie de “S” es la integral (es decir, la suma de infinitas cosas infinitamente pequeñas) y el subíndice de cuerpo nos dice simplemente cuales son los elementos a los que aplicamos la integral.
Bien, ahora solo nos queda definir la intensidad del campo eléctrico, E. (como ya he dicho arriba muchas veces se llama simplemente campo eléctrico a la intensidad de éste).
El campo eléctrico creado por una carga i en un punto P, puede calcularse a partir de la ley de Coulomb
Y de nuevo se puede formular el teorema de superposición como:
Vemos que esto es consecuencia del principio de superposición de fuerzas, solo hemos dividido entre Q todos los miembros de la igualdad.
Finalmente voy a introducir tres conceptos que son de muchísima ayuda para hacer cálculos con distribuciones continuas de carga, las densidades de carga; Las densidades de carga son análogos a las densidades de masa que todos conocéis (por lo menos la densidad volumétrica de masa seguro que sí) básicamente nos dicen en una región muy pequeña del espacio cuanta carga hay por unidad de longitud, superfície o volumen. Se obtienen dividiendo una carga muy pequeña (dq) por una longitud, superfície o volumen muy pequeños (dl, dS, dV).
Y hasta aquí la ley de Coulomb; en el próximo artículo hablaremos sobre algunos conceptos más del campo eléctrico e introduciremos la ley de Gauss (a veces llamado teorema de Gauss).
Hasta la próxima.
- Concepto muy importante porque entenderlo es clave para el siguiente artículo. [↩]
- El módulo de un vector recordemos que es siempre un número positivo. [↩]
- En realidad la fuerza depende de otra cosa más, el medio en el que se encuentran las cargas, pero vamos a suponer que todo pasa en el vacío. [↩]
- Estaréis hartos de que repita “por convención” todo el rato, pero es que quiero dejar claro que todo esto no es más que una convención. [↩]

The [De Thomson a Bohr, historia de un átomo] 0-Conceptos previos 4: Ley de Coulomb by Roger Balsach, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.


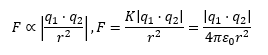
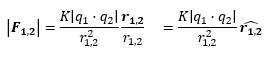
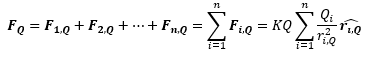
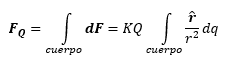
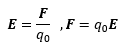
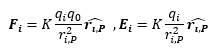
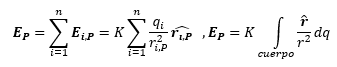



{ 3 } Comentarios
“El concepto de acción a distancia ha ocasionado muchos dolores de cabeza a los físicos desde siempre, ya que es un concepto bastante anti intuitivo?”… Roger : leyendo – el fotón – en el tamiz . Pedro sostiene esto “Por lo tanto, sabemos que si tenemos dos cargas en el espacio y se repelen, no lo hacen instantáneamente. Los fotones responsables de la repulsión tienen que viajar de una carga a la otra a la velocidad de la luz.” . mi pregunta es si esta teoría que introduce los fotones virtuales ayuda a quitarles en algo ese dolor de cabeza a los físicos . O son cosas distintas y yo estoy metiendo cuántica donde no debo ?
Si, para hablar de fotones virtuales necesitamos hablar de física cuántica. Como habrás visto, en el artículo no hablo de teoría de campos, sino teoría clásica de campos, existe otra mucho mas complicada (y mucho mas exacta) que es la teoría cuántica de campos. Y si no voy errado (este tema sobrepasa mis conocimientos de largo) los fotones virtuales son parte de esa teoría.
Espero haber respuesto tu pregunta, Roger
Roger : gracias por tu respuesta y felicitaciones por tu trabajo , me ha sido de gran ayuda , Leo todas tus entradas .
Escribe un comentario