|
La serie “El computador mágico” está disponible también en forma de libro. |
Hemos dedicado los últimos capítulos de esta serie sobre todo a representar números en notación binaria y a operar con ellos. Incluso hicimos un sumador con lógica combinacional. Pero se nos ocurren más operaciones que podríamos hacer con ellos, ¿verdad? Como mínimo, podríamos querer restar, multiplicar y dividir números. Podríamos querer además hacer operaciones lógicas, como AND u OR de dos operandos, o incluso operaciones individuales sobre sus bits, como máscaras y desplazamientos. Podríamos comprobar si un valor es mayor que otro. O incluso operaciones matemáticas más complejas, como potencias, trigonometría, logaritmos… yo qué sé, las posibilidades son infinitas.
Pues eso es lo que vamos a hacer hoy: hacer un bloque funcional que se encargue de las operaciones aritméticas y lógicas entre palabras, al que llamaremos unidad aritmético-lógica.
Para ello necesitamos primero definir qué es una palabra, pero no la definición en castellano, obviamente, sino la definición en el contexto de la arquitectura de los ordenadores. Incluso dentro de ese mundillo hay ligeros matices sobre lo que significa palabra, así que yo voy a dar una definición y a tratar de ceñirme a ella (si luego necesitamos matizarla, ya lo haremos). Y lo voy a hacer en forma casi tautológica: una palabra es la unidad de información con que opera la unidad aritmético-lógica del ordenador.
Si has entendido lo que acabo de decir, probablemente es porque ya sabías lo que es una palabra. Y de hecho, también lo que es una unidad aritmético-lógica. Así que vamos a ir describiendo todo y verás como al final se forma la imagen completa en tu cabeza.
Nosotros vamos a usar un tamaño de palabra de 16 bits. Supongo que no te sorprende si te digo que los ordenadores más comunes utilizan palabras de 8 bits, 16 bits, 32 bits, 64 bits (lo más habitual del mercado de consumo ahora mismo)… De hecho, ¿no recuerdas que dijimos que se solía representar los números precisamente con esos tamaños? Ahora ya sabes el motivo.
A menudo se usan otras definiciones para la palabra, como puede ser el ancho del bus de datos o la cantidad de información que puede direccionar la memoria principal con un solo acceso o con una sola dirección, pero como todo eso son cosas que aún no hemos visto, vamos a quedarnos con la nuestra de más arriba. Además, con el nivel de profundidad con que estamos viendo esta serie, todas esas definiciones son equivalentes (en los ordenadores reales, en cambio, no tiene por qué ser la misma cosa).
Supongo que, a poco que no hayas vivido en una cueva en los últimos años, sabes que existe una unidad llamada byte, compuesta de 8 bits. No se suele traducir al español, pero cuando se hace, se utiliza el vocablo octeto. Como hoy en día todos los ordenadores utilizan múltiplos de 8 bits para casi todo, es muy habitual utilizar los bytes como unidad de medida.
Por consiguiente, una palabra no son más que esos 16 bits puestos uno al lado del otro.
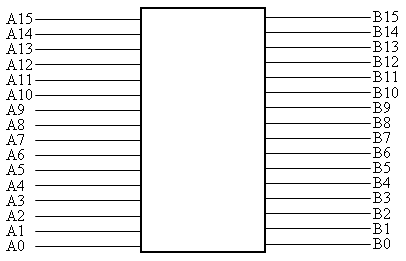
A15 A14 A13 A12 A11 A10 A9 A8 A7 A6 A5 A4 A3 A2 A1 A0
Y para simplificar, vamos a llamar a todo eso simplemente A.
Cuando estamos mostrándolo de manera gráfica, podemos dibujar las 16 rayas. Por ejemplo, en el siguiente dibujo vemos 16 líneas de 1 bit como entradas en un circuito combinacional:
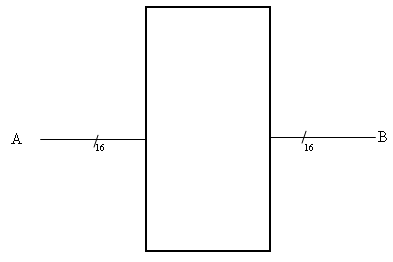
Pero, claro, eso es un incordio, así que habitualmente lo resumimos en una sola línea, en la que representamos el número de bits que tiene con una raya cruzada (o a veces ni eso, y tenemos que deducirlo del contexto, como haremos más adelante):
Así que vamos ahora con la unidad aritmético-lógica. La unidad aritmético-lógica no es más que un circuito combinacional que tiene:
- Varias entradas de datos. Fíjate en que esas entradas no son de un bit, como solían ser hasta ahora, sino que cada una de esas entradas tiene 16 bits (o el tamaño que corresponda en cada unidad aritmético-lógica, claro).
- Una o varias salidas de datos. Lo mismo: de 16 bits.
- Una entrada de control, que le indica a la unidad aritmético-lógica la operación a realizar. El número de bits que tenga dependerá del número de comandos diferentes que queramos poder enviarle a la unidad aritmético-lógica (luego lo veremos con más detalle).
- Opcionalmente, una o varias salidas de flags (algo así como indicadores, en inglés). De nuevo, el número de bits que tenga (es decir, el número de flags) depende de lo que estemos haciendo (también lo veremos).
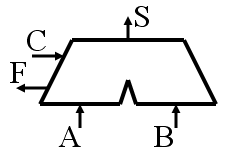
El símbolo para la unidad aritmético-lógica es habitualmente algo como lo siguiente:
En este caso hemos dibujado una unidad aritmético-lógica con dos entradas de datos y una salida, así como la entrada de control y la salida de flags.
Por cierto… ¿no te cansas de leer tantas veces “unidad aritmético-lógica”? Si tú te cansas de leerlo, imagínate lo que me canso yo de escribirlo. La mayoría utiliza el acrónimo ALU para referirse a ella, del inglés Arithmetic-Logic Unit. Así que eso lo que haré yo a partir de ahora: usar simplemente ALU.
Nosotros vamos a definir una ALU muy sencillita, que solo tenga cuatro comandos posibles:[1]
- Sumar (SUM): suma A más B y deja el resultado en S. Es decir, S=A+B (suma aritmética, no OR binario; no te confundas).
- Cero (CERO): pone un 0 en S. Es decir, S=0.
- Decrementar (DEC): resta 1 a lo que entra por A y deja el resultado en S. Es decir, S=A-1.
- Transferir (TRANS): transfiere el valor de B a S. Es decir, S=B.
Como tenemos 4 operaciones posibles, podemos, por ejemplo, codificarlas con 2 bits:
|
Comando |
C1 |
C0 |
|
SUM |
0 |
0 |
|
CERO |
0 |
1 |
|
DEC |
1 |
0 |
|
TRANS |
1 |
1 |
Así que la entrada C de nuestra ALU tiene únicamente 2 bits de ancho.
El único flag que genera esta ALU tan simple es el de desbordamiento: si la operación de suma da un valor mayor de lo que se puede representar o si la operación de decremento devuelve un valor menor de lo que se puede repreentar, este flag vale 1; en caso contrario, vale 0.
Como ves, las operaciones son muy sencillas. En fin… decir que eso son operaciones aritméticas y lógicas requiere un esfuerzo considerable de imaginación. Prácticamente, hay solo dos operaciones aritméticas (SUM y DEC), ninguna operación lógica y hay dos (TRANS y CERO) que difícilmente podríamos llamar “operaciones”. Bueno… claro… es que hemos definido una ALU muy-muy sencilla, con lo mínimo absoluto necesario para poder seguir avanzando. Otras ALUs más completas y más reales tienen comandos para:
- Muchas operaciones aritméticas, como restar, multiplicar…
- Operaciones lógicas, como hacer el AND de las dos palabras, el OR…. Fíjate en que siempre hemos definido el AND de dos bits, no el de dos palabras. Generalmente se define que una palabra vale, desde el punto de vista lógico, 0 si todos sus bits son 0; y 1 en caso contrario. Y así, el AND ya se puede hacer el AND sobre estos “bits virtuales” que son la palabra completa.
- Comparaciones entre dos palabras, determinando cuál de ellas es mayor, si son iguales, etc.
- Operaciones lógicas de bit, como hacer el AND del primer bit de A con el primer bit de B, y poner el resultado en el primer bit de S; y eso para los 16 bits. Esto se llama bitwise AND (que no tiene traducción fácil… algo así como “AND bit-a-bit”). Imaginarás que también hay bitwise OR, bitwise XOR,… O también puede hacer desplazamiento de las palabras: mover cada uno de los bits de la palabra un paso o varios hacia la izquierda, o hacia la derecha, rellenando con 0s o con 1s, o con lo que salga por el otro extremo… en fin, muchas posibilidades.
- Incluso operaciones mucho más complejas, como trigonométicas, logarítmicas…
Si eso ocurre, lógicamente, no nos valdrán con 2 bits para el comando C, porque a lo mejor necesitamos codificar… yo qué sé… 400 comandos distintos. Puede que necesitemos 4 bits u 8 bits ó 20 bits ó más. Y además no tienen por qué tener dos entradas, sino que pueden tener muchas más. Y lo mismo para la salida: no tienen por qué tener una, pueden tener más. Además de que, como ya hemos visto, la palabra (es decir, el tamaño de A, B y S) no tiene que ser solamente de 16 bits, sino que puede ser de otros tamaños.
Pero fíjate en lo más importante. Céntrate en esto. Lo más importante es lo siguiente: tenemos un montón de entradas (los 16 bits de A, los 16 bits de B y los 2 bits de C) y unas cuantas salidas (los 16 bits de S y el único bit de F). Lo que obtengamos en la salida dependerá únicamente de lo que hayamos puesto en las entradas. Ya hemos estudiado la lógica combinacional, así que sabemos que existe un circuito de puertas lógicas que es capaz de construir esa ALU. Ese circuito será sencillo, complicado, barato, caro, pequeño o grande… pero está compuesto única y exclusivamente por puertas lógicas conectadas de una forma más o menos astuta. Relee este párrafo hasta que lo hayas interiorizado.
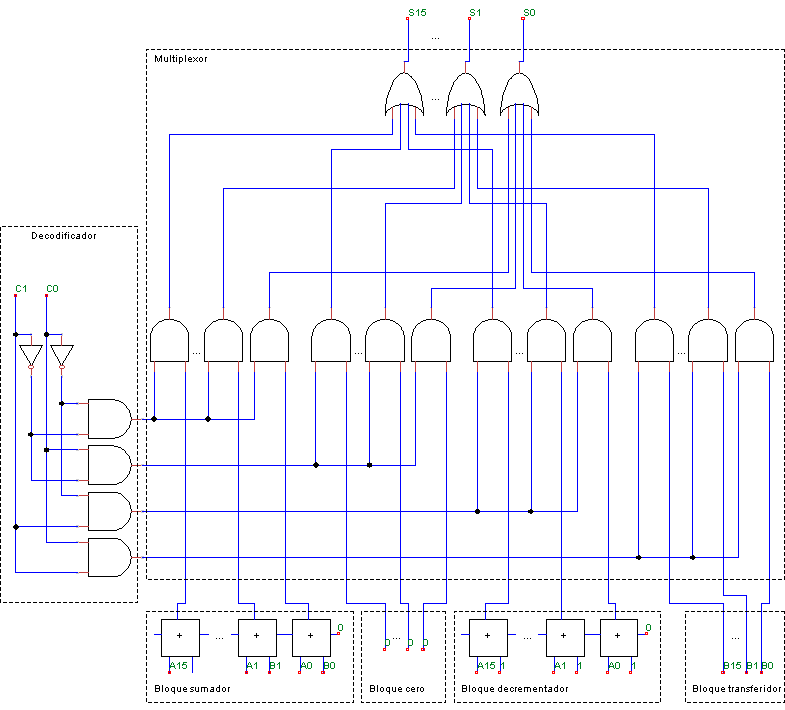
Con el conocimiento que has ido adquiriendo a lo largo de esta serie, ya tienes suficiente para diseñar tú mismo esta ALU tan sencilla. No espero que lo hagas, ya que hemos ido muy rápido y sin hacer ejercicios, pero… ¿quieres que la hagamos para que veas que es verdad? Aquí la tienes:
Espero que, aunque no se te ocurriera cómo hacerlo, al verlo sí entiendas todo lo que hay ahí. La parte inferior son los cuatro bloques que hacen las operaciones básicas (la cajita con el + es simplemente el sumador de un bit que ya vimos en su momento). El bloque de la izquierda se llama “decodificador”, y simplemente convierte los valores de la operación c1c0 en algo que sea más fácil de utilizar por el siguiente bloque, que es un multiplexor. Vamos a dedicarle unas líneas, porque nos hará falta más adelante. Lo que hace es que si la entrada es un 0 en binario (es decir, c1=0 c0=0), activa la salida número 0 y desactiva las demás (es decir, pone un 1 en la salida número 0 y un 0 en las demás); si la entrada es un 1 en binario (es decir, c1=0 c0=1), activa la salida 1; y así sucesivamente. No es difícil deducir que si el decodificador tiene n entradas, tendrá 2^n salidas (pero solo una de ellas será un 1; el resto serán un 0).
El multiplexor simplemente tiene 4 entradas (de 16 bits cada una, en este caso) y pone en la salida la que corresponda a la que le está diciendo el decodificador. Fíjate en que, en realidad, nuestra ALU calcula las 4 operaciones básicas (suma, borrado, decremento y transferencia), pero debido al decodificador y al multiplexor, solo la que corresponda al comando seleccionado por C se pone en la salida.
Los siguientes símbolos son los que se suelen utilizar para representar estos dos componentes. Recuérdalos, porque los necesitaremos más adelante. A veces se asume que la entrada al multiplexor es una elección binaria (es decir, n entradas) y a vece se asume que ya está “decodificada” (es decir, 2^n entradas), pero tendrás que deducirlo del contexto.
Como decía, no espero que hayas llegado tú solo hasta el diseño de este circuito, pero sí que una vez que lo hayas visto, te hayas dicho “pues es verdad, tampoco es tan difícil, lo entiendo todo”. No hemos hecho la parte que genera el flag de salida… hazlo tú mismo si quieres.
Existen formas más eficientes (pero menos didácticas) de hacer este mismo circuito. Y si en vez de cuatro operaciones sencillitas, como es el caso, tuviéramos un centenar de operaciones, podría ser que el diseño de la ALU ocupara un libro entero de cientos de páginas… pero lo que tienes que tener claro es que la salida solo depende de las entradas y del comando seleccionado, y por lo tanto existe un circuito combinacional que implementa esa ALU.
¿Y por qué tanto hincapié en este asunto? Porque en el próximo artículo introduciremos un nuevo componente, el biestable, que nos permitirá adentrarnos en un nuevo concepto: los circuitos secuenciales.
- Este diseño está basado en el de la ALU de simplez, diseñado y descrito por Gregorio Fernández Fernández en su libro “Curso de ordenadores. Conceptos básicos de arquitectura y sistemas operativos“, que será una de las referencias que daremos al final. Según vayamos avanzando iremos viendo de todos modos que nuestro diseño es aún más simple que el suyo. [↩]

The Computador mágico XIV – Unidad aritmético-lógica by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.






{ 6 } Comentarios
Pues, honestamente, después de ver el circuito, sigo sin enterarme de nada. :-/
Brigo, ¿qué es lo que no entiendes? A lo mejor puedo explicarlo de otro modo…
No se entiende muy bien este articulo porque hablas de una ALU y se hace la siguiente lista mental si es que sigue el mismo razonamiento que yo.
Cuando ves el dibujo de la ALU y tu texto refuerza la idea lo que piensas es esto:
Entra A y B a la ALU C selecciona la operacion a realizar Se realiza SOLO la operacion seleccionada Sale por S el resultado.
Tu ALU perfectamente valida como ejemplo sin embargo hace:
Entra A y B a la ALU Se lleva A y B a todas las operaciones donde se usan Se hacen todas las operaciones internamente Se ponen a cero todos los resultados excepto el de la operacion seleccionada Se mezclan todos los resultados pero como estan todos a cero excepto el seleccionado S es el deseado
Se comio los saltos de linea el wordpress asi que me explicare mas claro. En tu articulo hasta antes de la imagen describes la ALU como una especie de selecionador. Entran A y B solo al circuito de la operacion seleccionada y sale el resultado por el otro lado. En la imagen y en la explicacion de despues A y B entran a todas las operaciones a la vez y se calculan su resultados. Sale solo el resultado seleccionado. Van a funcionar cualquiera de los dos diseños pero el de la imagen te deja el culo torcido porque esperabas otra cosa.
Lo siento por el triplepost. Una opcion seria poner la imagen poner la imagen despues del texto o hacer un diseño alternativo con un demultiplicador en las entradas A y B y sin multiplexor en las salidas. Asi cuadraria mas las expectativas.
Por cierto gracias por tus articulos. Son muy interesantes e instructivos.
Lo que dices es cierto. Lo que pasa es que intentaba que el diseño concreto fuera un detalle sin importancia. Lo verdaderamente importante es: tengo unas cuantas entradas y unas cuantas salidas, y las salidas depende exclusivamente de las entradas; por lo tanto, existe un circuito combinacional que permite hacer eso… el que yo he dibujado es solo uno de los posibles, y además probablemente no el mejor.
Escribe un comentario