Entre el mito y la realidad.

En el artículo anterior de esta serie musical y científica a la vez decíamos que ahora hablaríamos acerca de las reglas que gobiernan la Armonía. ¿En qué consisten exactamente? ¿Tienen algún fundamento científico?

Los legos ven la Armonía casi como un arcano, una suerte de ciencia difícil de comprender, llena de fórmulas para saber organizar los sonidos en forma coherente. El hecho de que su estudio corresponda a los cursos superiores de música contribuye a crear esta imagen.

Pero hay algo casi mitológico en todo ello. En realidad, si despojamos a la Armonía de toda la reglamentación que contiene, quedará muy poca cosa. ¿Y por qué haríamos ese despojo? Pues para confrontar el reglamento y la ciencia.

Y eso es lo que comenzaremos a hacer a partir de ahora.

El término “Armonía” tiene un contexto de cosa armoniosa, equilibrada, bien proporcionada. Ese concepto, aplicado a la combinación de sonidos simultáneos, dio por resultado esta disciplina que aún no ha perdido su significado estético. Pero muchos creen que es una parte de la ciencia.

Esta creencia parece deberse al origen de los estudios realizados con cuerdas en la antigua Grecia.  Más tarde se comprobaría que aquellos cálculos se correspondían exactamente con los armónicos naturales que una cuerda puede producir.  Se observó que ese fenómeno de la naturaleza era algo tan equilibrado y matemáticamente bien proporcionado  que por esa razón  contribuiría, más tarde, a originar la propia etimología musical del término Armonía. En efecto, si la música se fundamentaba en la forma como esos sonidos se relacionan naturalmente entre sí, debía necesariamente sonar “armoniosa” al escucharla y, por lo tanto, agradable y perfecta.

Ahora bien, ocurre que alrededor de la relación entre la música y la matemática hubo nombres como Pitágoras y Aristógenes, quienes calcularon la escala diatónica, que no es otra que la conocidísima do-re-mi-fa-sol-la-si-do. Todos hemos oído hablar de esta escala, porque todavía mantiene vigencia en el siglo XXI, lo que da una idea de su trascendencia.

También hay que tener en cuenta que con las notas primera, tercera y quinta de esta escala, se puede formar el no menos célebre acorde do-mi-sol, llamado acorde “perfecto”, pues en su propio origen se le consideró la combinación más perfecta de sonidos simultáneos, sin disonancias que enturbien la pureza de la combinación.

A continuación podéis escuchar cómo suena este “acorde perfecto”:

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

El “acorde perfecto” fue, y es, una herramienta muy importante. Tan importante  como que constituye la base firme de casi toda la música escrita hasta el presente. Se puede tocar no sólo a partir del “do”, sino partiendo de cualquier otra nota, lo que le hace un recurso muy maleable. Además, las mismas notas del acorde tocadas en forma sucesiva son parte importante de muchas melodías -  aun sin  acompañamiento de acordes, como en el siguiente ejemplo:

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

Detengámonos un momento entonces, para ver más de cerca el fenómeno natural que dio origen a la escala do-re-mi-fa-sol-la-si-do.

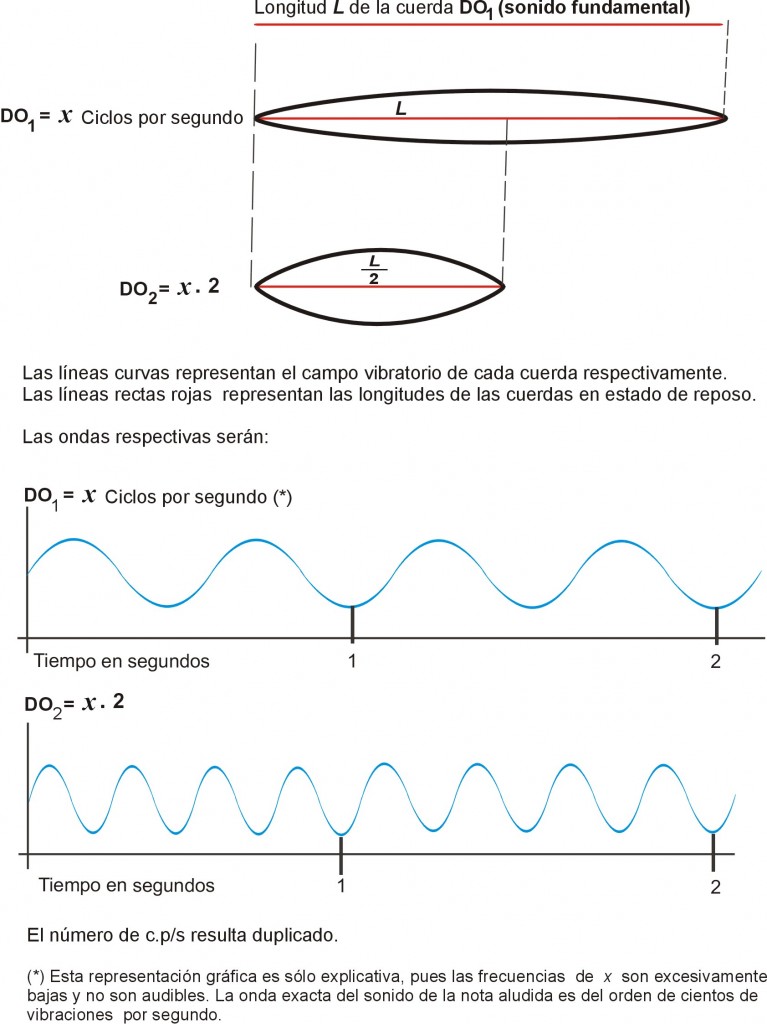
Veamos primero que la escala empieza y termina en un DO. ¿Ambos son iguales? No, pues el que cierra la escala tiene exactamente el doble de vibraciones por segundo que el que la empieza. Esto quiere decir que si la cuerda del DO inicial tiene x vibraciones por segundo y una longitud L , entonces el segundo DO (el que cierra la escala) tendrá  x·2 vibraciones por segundo. Esto se obtiene dividiendo la cuerda por la mitad, es decir, la longitud será L / 2.  Al sonido fundamental se le llama primer armónico, y de ahí en adelante siguen numerándose ordinalmente. El ejemplo siguiente muestra cómo se obtiene una cuerda que suene igual al armónico 2 del DO fundamental:

Este procedimiento produce un intervalo llamado octava justa, nombre que proviene de que la distancia entre ambos sonidos es exactamente de 8 notas, y es “justa” porque la afinación coincide con los armónicos. Aplicado a cualquier expresión fraccionaria, el mismo método permite representar cualquier otro intervalo “justo”, como por ejemplo la “quinta justa” que resulta de dividir la cuerda en un tercio de longitud. Si la nota DO sigue siendo el sonido fundamental, un tercio de su longitud corresponderá al tercer armónico, que es la nota SOL, y se halla a 5 notas de distancia del DO. En estos casos,  o cualquier otro, conociéndose la longitud de cada una de las cuerdas, es posible calcular las  vibraciones (ciclos) por segundo de los sonidos que forman el intervalo, es decir, la relación armónica entre ambos sonidos.

A continuación podéis escuchar cómo suena una octava, es decir, una nota y después la misma nota de la escala superior (y con el doble de ciclos por segundo), seguidos por un acorde de ambas notas tocadas simultáneamente:

Octava:

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

Y ahora el mismo ejemplo, pero con las dos notas separadas no por una octava, sino por una quinta justa:

Quinta justa:

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

En Acústica, no obstante, la identificación de intervalos se generaliza prescindiendo de las notas. Para representar una relación armónica se utiliza una expresión fraccionaria, o razón, donde tanto el numerador como el denominador se refieren a los armónicos obtenidos, según sea la fracción en que una cuerda (o columna de aire) resulta dividida. Así, el sonido fundamental (longitud 1) será expresado por la razón 1/1 y se le llama primer armónico. La octava justa, que vimos recién, quedaría representada por la razón 2/1, donde el numerador expresa el 2° armónico y el denominador el primer armónico. La quinta justa, será representada por la razón 3/2 , pues los armónicos de referencia son 3 y 2.

Ahora examinemos más de cerca algo que suele causar confusión, por igual, entre los músicos y quienes tienen formación científica. Por ejemplo, la notación de algunas relaciones armónicas como 3/2, 4/3,  16/15, etc., ¿qué significan exactamente si queremos saber la frecuencia de cada sonido?

Un convenio no muy feliz.                                                                 

Comencemos por algunas definiciones más precisas. El numerador y el denominador corresponden, respectivamente, a los armónicos según los cuales los sonidos que forman el “intervalo” tendrán una determinada frecuencia. Por “intervalo” se entiende la relación de frecuencias entre ambos sonidos. La unidad de medida de la frecuencia – o sea, la medida de cuántas vibraciones por segundo tiene una cuerda (o también una columna de aire dentro de un tubo) – es el hercio (Hz) y en la terminología de los músicos equivale a la afinación. Pero ni el numerador ni el denominador expresan por sí solos una frecuencia: únicamente se refieren al número ordinal del armónico.

La operación que permite un cálculo en Hz tiene que partir de conocer la frecuencia del sonido fundamental de la serie armónica, y eso es suficiente. No nos perdamos en el razonamiento tratando de identificar notas, porque eso es un recurso para ayudar a que los músicos lo comprendan. De hecho, la propia serie armónica también se escribe en el pentagrama con notas, lo que en realidad es una terrible imprecisión.

El cálculo se hace observando la medida en Hz del primer armónico y multiplicando esa frecuencia por el número de orden del armónico cuya frecuencia queremos conocer. Por ejemplo: 3/2. Si queremos saber lo que esto significa en Hz, tenemos primero que establecer cuál será la frecuencia del sonido fundamental de la serie armónica. Si decimos que el número 1 tiene una frecuencia de 220 Hz , quiere decir que el segundo armónico de la serie (se representaría como 2) tendrá el doble, o sea 440Hz y es el LA central del piano. A su vez, el armónico 3 del sonido de 220 Hz tendrá 660 Hz (220 x 3 = 660) y corresponderá a la nota MI central del piano. Esto forma el intervalo llamado “5ª justa” en la música que, una vez determinado que el armónico 2 = 440Hz y el armónico 3 = 660Hz, permite afinar el instrumento. No importa si luego se tocan las dos notas a la vez (acorde) o sucesivamente (melodía).

El inconveniente de este procedimiento, que es el más conocido, consiste en que puede ser forzoso calcular una transposición para poder ubicar los sonidos en forma de escala. Por ejemplo, si queremos conocer la frecuencia del sonido que se halla a 1 tono de otro cualquiera, la relación armónica será 9/8. Muy bien, pero si la fundamental de la serie armónica sigue siendo la nota LA de 220 Hz su armónico 8 será 220 x 8 = 1.760 Hz y su armónico 9 será 220 x 9 = 1.980 Hz que corresponderá a la nota SI.

A simple vista es evidente que estas frecuencias son muy alejadas del LA central de 440 Hz, que es el sonido desde donde hemos decidido empezar la escala. ¿Cómo podemos hacer para calcular la frecuencia de la nota SI que se halla a 1 tono del LA central de 440 Hz? Lo primero a observar es que la relación es con el armónico 8 del LA, en lugar del 2. Si bajamos las frecuencias dividiendo por 4, tenemos: 1.760/4 = 440 Hz (LA central) y 1.980/4 = 495 Hz (SI central), con lo que hemos transpuesto a la región central del piano la relación 9/8 y la escala puede continuar formándose. Esta operación se vuelve necesaria para cada nota de cualquier escala que sea, y no solamente la que comenzaría por la nota LA central.

Por eso hay una forma más práctica de hacer el cálculo, para evitar la necesidad de hacer transposiciones. Podemos adoptar una frecuencia cualquiera y multiplicarla directamente por la fracción que representa la relación armónica, es decir, por ejemplo, 440×3/2 = 440×1,5 = 660 Hz (frecuencia del MI central que forma una quinta justa con el LA, también central). O bien, 440×9/8 = 440×1,125 = 495 Hz (frecuencia del SI central, a un tono de distancia del mismo LA).

Obsérvese que el resultado de la operación se refiere siempre a la frecuencia del sonido equivalente al armónico de orden más alto en la relación. Luego, la nota siguiente de la escala que comienza por el LA se llamará DO. Y digo “se llamará”, por una razón que veremos en seguida. Ese tercer sonido de la escala de La, en la serie armónica corresponde al N° 5 y la relación será 5/4. Por este segundo método de cálculo, tendríamos que 440×5/4 = 440×1,25 = 550 Hz que es la frecuencia del DO en cuestión. Ahora bien – y he aquí un gran problema que demoró cierto tiempo en ser descubierto -, ¿dónde se tocará ese DO en un teclado como el del piano, el clavecín o el órgano? Pues para que pueda haber dos intervalos consecutivos de 1 tono al empezar la escala, vean ustedes dónde habrá que tocar ese “DO”:

Esa tecla negra que ahora habría que usar se llama “do sostenido”, y no simplemente “DO”. Pero dejemos esto para un próximo artículo, pues lo que parece un pequeño detalle, es todo un tema que terminaría revolucionando hasta la manera de componer, incluso hasta hoy día.

Siguiendo con el tema que veníamos, como hizo falta una generalización que tuviese valor para cualquier caso particular, todos estos cálculos fueron resumidos conviniendo en que tanto el numerador como el denominador no se refieren a ninguna nota específica. Si en vez de la nota LA tomamos como referencia otro sonido cualquiera, por ejemplo de 20Hz (obsérvese que ya no hablamos de notas) su armónico 2 será de 40Hz y el armónico 3 será de 60Hz. A esas frecuencias les podemos dar nombres de “notas”, si queremos, pero esas notas siempre estarán formando una “quinta justa” y está convenido que se representa escribiendo 3/2.

Hay que reconocer que esta no es una forma muy feliz de representar un hecho de la Física. En primer lugar, esa manera de representar una relación armónica no permite calcular la medida de un intervalo, pues esa medida es una función logarítmica y no lineal, lo que quiere decir que el intervalo no se calcula por simple resta de las frecuencias. Asimismo, tampoco tiene sentido interpretar que 3/2 equivale a la operación aritmética de división, pues 3:2=1,5, por sí solo, carece de sentido para medidas en Hz. Pero hace más de dos mil años, cuando todo este tema se empezaba a estudiar, no existía la noción de Hz, ni mucho menos la de logaritmo. Por lo tanto, ahí arraiga un problema que sigue hasta hoy cuando se trata de conciliar la terminología de la Física con la de los teóricos de la música. Aun en buenos libros de Acústica, la descripción de las relaciones armónicas no menciona los equivalentes en Hz y la descripción se limita a la presentación de expresiones fraccionarias como 2/1, 3/2, etc., asociadas a las notas, evidentemente con la intención de hacer esto más comprensible para los músicos. Puede parecer hasta disparatado, pero ni siquiera hay acuerdo universal acerca de la numeración de las notas (la nota La de 440 Hz puede ser de orden 3 ó 5, según sea que se adopte como referencia, o no, el teclado del piano, pero eso no hace que varíe la escritura de la nota en el pentagrama).

Todo ello suele dificultar la comprensión de los cálculos que deben hacerse, a causa de que el fenómeno acústico no se presenta reducido a una fórmula matemática, sino simplemente escribiendo el número de orden más alto de un armónico encima de otro de orden más bajo, separando ambos con una línea, apareciendo así escrito como un quebrado.

De todos modos, esto es lo que está convenido y, entendiéndolo, es posible representar cualquier intervalo incluso con múltiplos de armónicos de orden más bajo. Por ejemplo, 16/15 expresa la relación entre el armónico 16 = 2^ 4 y el armónico 15.

Sobre esta base, Pitágoras y Aristógenes dedujeron no obstante la escala diatónica. Pero sus cálculos no fueron equivocados, porque estuvieron basados en la medición precisa de las dimensiones de las cuerdas y luego en comprobaciones experimentales por el método de la audición, hasta llegar a formular la escala como una combinación general de sonidos sucesivos para hacer música.

La forma en que llegaron a esa conclusión fue muy ingeniosa. Primero calcularon una sucesión de intervalos de “quintas justas”: FA-DO-SOL-RE-LA-MI-SI. Luego, ordenando los mismos sonidos en forma de escala, resultó una sucesión ordenada de tonos y semitonos: DO-RE-MI-FA-SOL-LA-SI. Tal vez a nosotros eso pueda parecernos sencillo, pero ellos tuvieron que descubrir, primero, que la frecuencia es inversamente proporcional a la longitud de una cuerda, y después que el punto de partida para formar la escala es el intervalo de 5ª justa.

La escala de Pitágoras difiere de la de Aristógenes en el tamaño del semitono, aunque ambos llegaron a una misma conclusión en cuanto a la distribución periódica de los tonos y semitonos. Es interesante saber al respecto, que los griegos entendían la escala en sentido descendente y partían de la nota MI (mi-re-do-si-la-sol-fa-mi), al contrario de nosotros que la entendemos en sentido ascendente, pero de cualquier manera la disposición periódica de los intervalos es la misma, por cualquier nota que se la empiece, sea ascendiendo o descendiendo:

Escuchemos cómo suena una escala completa:

Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.

PITÁGORAS

Esta disposición no es al azar. El problema para construir cualquier escala es que debe cumplir con tres condiciones.

La primera de ellas es que debe  cerrarse en el ámbito de la octava justa. Esto permite que la sucesión de notas sea repetible a diferentes alturas, lo cual posibilita que varias voces – e instrumentos – más agudos o más graves, puedan cantar y tocar en conjunto armonizando entre ellos.

La segunda condición para una escala es que la división de la octava justa en intervalos más pequeños permita disponer de una cantidad suficiente de sonidos para ordenarlos en diferentes combinaciones, y que esas combinaciones no se agoten rápidamente. Se habría optado por un conjunto de 7 sonidos porque cumple con esta condición, pero porque también cumple con la tercera:

Esta tercera condición es que permita la combinación de sonidos simultáneos sin producir pulsaciones. Las pulsaciones, o batimientos, se oyen como una oscilación en la afinación del sonido, y puede ser un efecto bastante molesto si la escala ofrece pocas formas de manejar este fenómeno, e incluso evitarlo, si se quisiera. La escala diatónica fue la solución hallada para cumplir con esta condición, permitiendo la formación del acorde “perfecto”, que como ya dijimos, fue considerado la combinación mejor equilibrada de sonidos simultáneos.

Por supuesto, hay otras combinaciones posibles para formar acordes, y permiten el empleo de diferentes grados de disonancia, siempre dentro de las relaciones armónicas que ordenan los intervalos. Pero el tiempo transcurrido hasta que dichas combinaciones fueron siendo aceptadas fue bastante considerable, y, para su uso, lleno de reglas y procedimientos.

En sucesivos artículos volveremos a hablar de la escala diatónica, dada la importancia histórica que tiene. Fue una raíz científica que alimentaría la música por siglos.

Ahora cabe preguntarnos qué es la perfección – por lo menos en la música -  puesto que mucho más que lo que terminamos de ver no es rescatable dentro de esa disciplina llamada “Armonía”. Tampoco del Contrapunto, que es el antecedente histórico del concepto de Armonía codificado en los textos de enseñanza. Puede ser que algunos discrepen con esta conclusión, pero el hecho es que las reglas para combinar sonidos en la música tienen mucho más que ver con el subjetivismo que con la objetividad científica. Veamos por qué. 

Hacia la inalcanzable perfección.

El Imperio Romano absorbería mucho de la cultura helénica, y en la música dejaría una herencia que recogería, en parte, la cultura medieval que le siguió. La música de la Edad Media proseguiría desarrollándose sobre la escala diatónica, aunque con características propias que luego habrían de transformarse en las canciones de los trovadores, siempre sobre el modelo diatónico, hasta cristalizar en la polifonía (superposición de diferentes melodías) que habría de caracterizar a toda la música de occidente.

La polifonía, a su vez, llegaría a su esplendor durante el período barroco del siglo XVII. El estilo barroco hacía escuchar dos, tres y hasta cuatro o más melodías a la vez, ornamentándolas, haciéndolas dialogar entre ellas, unas imitando a otras,  ya fuese por medio del canto, tocándolas en una orquesta o combinando la orquesta con las voces. Se consideraba que éste era el género por excelencia para expresar al máximo la más libre fantasía creativa. En su época se consideró perfecto, y, mediante el uso de ciertas reglas, se obtenía un resultado muy apreciado.

Pero en el siglo XVIII se produciría una gran ruptura. La estética barroca pasó a considerarse excesivamente recargada para el buen gusto. La propuesta fue entonces un retorno a la simplicidad y la claridad. Juan Sebastián Bach fue calificado de retrógrado (y luego olvidado durante un siglo), porque seguía persistiendo en componer música polifónica en su estilo barroco, mientras la estética de los nuevos tiempos se fundaba en una sola melodía simple y elegante, acompañada casi exclusivamente con acordes que reafirmaran la tonalidad. Nuevas reglas fueron enunciadas, a fin de obtener los mejores resultados sonoros con este nuevo punto de vista. ¿Se habría alcanzado, finalmente, la perfección?

Durante el siglo XVIII se llegó a pensar que así era, y que las cualidades del sonido se podrían seguir investigando en la Física, pero independientemente, pues cualquier nuevo descubrimiento muy poca aplicación tendría en la música. Todo lo relativo a la música estaba sólidamente establecido en forma suficiente. En prueba de ello, existían límites a considerar para cualquier nuevo supuesto avance, a saber:

1) Si la escala diatónica y el acorde perfecto tenían base científica, se creyó estar a un paso de poder formular reglas de Armonía de base también científica, por el solo hecho del origen. Es decir, las reglas podían considerarse científicas, porque eran para aplicar la base científica de la música. El uso predominante del acorde perfecto para reafirmar la tonalidad provenía de considerar que ésa era la relación armónica más equilibrada posible, resultado del cálculo matemático, y la mejor para conseguir una sobriedad en la ordenación de los temas y la distribución de las tonalidades que componían la obra. De esta manera, por ejemplo, las disonancias eran tratadas como “notas extrañas”, término éste que significaba que no pertenecían al acorde perfecto. Por lo tanto, según las reglas de aquel período, toda disonancia debía ser “preparada” y “resuelta”, es decir, las disonancias eran un ornamento, pero no debían ser inesperadas y debían regresar necesariamente a formar un acorde perfecto consonante. Asimismo, el pasaje de una tonailidad a otra, también se regía por ciertas reglas basadas en el intervalo de quinta justa, entendiéndose que la mejor manera de cambiar de tonalidad era pasar de una a otra que estuviese – directa o indirectamente – en relación armónica 3/2 con la tonalidad principal, pues dicha relación armónica es la base de cálculo de la escala diatónica. La estética del siglo XVIII unificaba así la ciencia y la perfección formal. Se creía que, más allá de esas metas alcanzadas, nada que fuese superior podría existir para satisfacer tanto al oído como a la razón.

2) La propia naturaleza del sonido también parecía señalar límites a tener en cuenta. La cantidad de armónicos es matemáticamente infinita, pero no lo es materialmente, pues una cuerda no es divisible al infinito. Tampoco lo es una columna de aire en un tubo, aunque el margen sea mayor. En tanto una cuerda de un centímetro de longitud es virtualmente imposible hacerla sonar, en cambio un tubo igualmente pequeño sí puede producir un sonido, pero extremadamente agudo y quizá desagradable. La cantidad de sonidos utilizables que la Acústica podía revelar a la música parecía también por este lado haberse agotado definitivamente.

3) Otro límite importante, siempre observando las propiedades del sonido, también se creyó válido. El conjunto de los sonidos armónicos, clasificados en ciclos por segundo, no da una función lineal, sino logarítmica. Esto significa que cuanto más alto sea el número ordinal del armónico, menor será la diferencia de vibraciones por segundo entre armónicos consecutivos o muy próximos entre sí, pues hay una zona donde la curva logarítmica tiende a una recta. El oído casi no percibe la diferencia de afinación si se hacen oír esos sonidos de orden tan alto por separado, pues da la casualidad que la percepción auditiva también es una función logarítmica. No obstante, si ambos sonidos se oyen en forma simultánea, el oído sí percibe la mezcla. Pero si se prosigue aumentando los valores el oído deja finalmente de percibir las diferencias también en la mezcla. Por otra parte, si el sonido fundamental es de muy alta frecuencia, sus armónicos pertenecen al campo de los ultrasonidos que son inaudibles para  el ser humano, aunque hoy se sabe que los armónicos ultrasónicos pueden influir en la percepción de cualquier sonido audible. Si bien en el siglo XVIII aún no se habían realizado investigaciones concluyentes acerca de estos fenómenos auditivos, tratándose de todos modos de sensaciones bien perceptibles,  se concluyó  en que el tamaño de los intervalos útiles tenía un límite, así como también lo tenía el buen gusto del manejo de los timbres en las mezclas de armónicos. Pareció que a este respecto tampoco habría mucho más para hacer.

4) Sin embargo no se ignoró que, por interferencia, se puede producir una onda resultante de baja frecuencia y crear una disonancia entre armónicos y eso es perfectamente audible. Estas disonancias el oído no las percibe necesariamente como desagradables. Al contrario, infinidad de veces contribuyen a poder manejar el timbre, que es una de las cualidades inseparables del sonido. Una flauta no suena igual que un oboe. Tampoco la flauta tocando junto con un oboe suena igual que si toca con un clarinete. La causa está en cómo se interfieren entre sí los armónicos de las notas tocadas por diferentes instrumentos a un mismo tiempo. Los más diversos efectos así obtenidos son explotados en las técnicas de la orquestación. En esto también la estética del siglo XVIII creyó haber alcanzado las combinaciones orquestales más perfectas y elegantes, pues la sonoridad obtenida aplicando determinadas reglas armonizaba con el uso que se hacía de los acordes.  Así, la orquesta sonaba de una forma bien definida, cosa que se puede comprobar escuchando sinfonías  de Haydn, y de  Mozart, u otros autores del siglo XVIII, y comparando. Se percibe un estilo sonoro en común, muy característico.

Pareció perfecto, sí, pero surgieron los primeros desengaños. Ese prototipo sonoro no era el más apropiado para otra clase de expresiones. En el siglo XIX la Armonía se ampliaría, por necesidad, con el uso frecuente de acordes de diferentes clases. Los cambios de una tonalidad para otra se volverían más libres. Las orquestas sinfónicas introducirían algunos instrumentos muy poco usados en la orquesta clásica, y además iría  aumentando de tamaño hasta llegar a contar con 100 y aún más ejecutantes. Pero el problema volvió a repetirse una vez más. Nuevamente, la orquestación y la combinaciones de acordes parecieron haber alcanzado sus límites. La orquesta y la música de Wagner suenan muy diferente que en Mozart, pero, ¿y después, de ahí en adelante?

Desde luego, nada de esto fue dicho tal cual por nadie, aunque quedó implícito en el conjunto de reglas que buscaban asegurar la permanencia de un estilo juzgado como perfecto en cada época. Pero en ese juicio implícito es donde se revela la rutina, la falta de inquietudes, la parálisis de las investigaciones, el creer que los elementos disponibles para la música ya son suficientes, que no hay nada más que hacer sino seguir componiendo según la regla indica. Así fue como, repetidas veces en la historia, los músicos creyeron haber alcanzado la perfección, o estar muy cerca de ella, cuando súbitamente cayeron en la cuenta de que en realidad se había producido un estancamiento. Y en ningún caso la ciencia pudo contribuir en algo.

Ocurre que, en el manejo del conjunto de todos los elementos que la ciencia puede aportar, siempre hubo un hecho que separa definitivamente las reglas y la ciencia. Sin excepción alguna, las reglas fueron enunciadas con posterioridad a las obras musicales. Tal como ya hemos dicho, primero fue la música… Y después de juzgar que los procedimientos desarrollados por los mejores compositores sonaban bien, se los generalizó en los textos didácticos. Por este motivo es que las innovaciones en la música suelen ser irritantes y controvertidas: ¡Contradicen nada menos que los procedimientos de composición ideados por los mayores genios de la historia!

Pero eso no es ciencia.

Eso es un respeto excesivo que ha llevado repetidamente a no saber distinguir entre métodos de composición y procedimientos científicos, cuando no a anquilosamientos contra los que se ha reaccionado. No sería equivocado decir que cuando se teoriza demasiado en cuestiones subjetivas se mata el arte.

Hay un hecho al respecto que es digno de señalarse para evitar toda confusión cuando se coloca a la ciencia y el arte en falsa oposición. Si se quiere tener una idea de la influencia que la ciencia puede alcanzar a tener en el arte de los sonidos, hay que reconocer que más de dos mil años de música, toda ella diferente, pero fundada en un mismo principio armónico, no es un hecho que se pueda explicar como simple hábito rutinario. Actualmente sigue habiendo muchos compositores que utilizan la escala diatónica. Aunque no se atienen a las reglas tradicionales que vienen de los siglos pasados, siguen fieles a la tonalidad.

En el próximo artículo comenzaremos a ver, por eso, un camino de transformaciones iniciado sobre la base matemática que ha cimentado tantos estilos y géneros distintos de música.

Finalicemos, por hoy, con una cita para reflexionar:

“El hombre sólo ha producido dos cosas que merezcan la pena: el arte y la ciencia.”

Santiago Ramón y Cajal (1852-1934)  

The Música y Ciencia. 6) Atisbando en la Armonía by Gustavo Britos Zunín, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.