Hace unas semanas publiqué dos artículos contándoos, en primer lugar, mi pequeña pero persistente fascinación por el veterano concurso televisivo Cifras y Letras, luego describí brevemente su funcionamiento y una forma de construir un programa informático para resolver tanto las pruebas de letras como las de cifras. De estas últimas, en primer lugar describí, en el primero de los artículos cómo resolver el problema en un ataque por fuerza bruta (hay 30.965.760 fórmulas distintas posibles), y en el segundo, un método de optimización que permitía reducir fórmulas redundantes hasta que, al final, quedaba un fichero de 1.025.472 fórmulas que contenía a los casi 31 millones iniciales, fórmulas todas ellas que estaban representadas en Notación Polaca Inversa.
Dije entonces, y repito ahora, que no tengo la completa, total y absoluta certeza de que en este fichero de millón y pico de fórmulas no hubiese aún fórmulas redundantes; lo que he hecho es ejecutar un sinfín de problemas y luego comprobar a mano, en una tediosa tarea, que efectivamente todas las formas de resolución encontradas fueran diferentes… tras muchas fórmulas revisadas, me rendí: si hay alguna redundante, mala suerte… pero eso sí, de haber alguna, deben ser pocas.
Tampoco tengo la absoluta seguridad de que este fichero fuese capaz de resolver absolutamente todos los problemas que tendrían solución con un ataque por fuerza bruta… podría ser posible que, dado un cierto retorcido problema que sí que tiene solución, no se encontrara revisando el millón y pico de combinaciones del fichero. Así que, para quedarme tranquilo, he hecho millones de ejecuciones en las que generaba un problema aleatorio, y si no tenía solución revisando el fichero reducido, lo intentaba por fuerza bruta. Nunca he encontrado un problema que cumpliera esta condición… así que, en definitiva, asumo que el fichero reducido de 1.025.472 fórmulas es válido. Y si no lo es… lo siento, pero hasta aquí he llegado.
Una vez publicados ambos artículos, en los comentarios al segundo de ellos, cruzki nos avisó que la reducción de fórmulas equivalentes era un problema NP-completo “de esos de un millón de dólares” (o sea, que al afortunado que lo resuelva, alguien, no sé quién, le paga un millón), y ya ves, el ignorante de mí intentando resolverlo… ![]()
Y Antonio Villena, en varios comentarios, nos decía que, en primer lugar había escrito un programa genial, en base a un algoritmo de backtracking,[1] para resolver online los problemas. Ésta es la página donde puedes jugar un poco. Y luego el propio Antonio sugirió diferentes estrategias para optimizar el cálculo… Estas sugerencias me hicieron pensar sobre el asunto, y sí, Antonio tenía razón: incluyendo alguna restricción al problema inicial se puede mejorar el algoritmo… A darle unas pocas vueltas de tuerca a la solución se dedica este tercero y (¡espero¡) último artículo sobre las Cifras y las Letras…
Dije entonces, y repito ahora, que el objetivo de los artículos es en realidad ilustrar un método de optimización, es decir, cómo ir profundizando paso a paso en un determinado problema para obtener el algoritmo más eficiente posible para resolverlo. También dije que una optimización “dura” como la aquí mostrada sólo tiene sentido para resolver problemas que van a repetirse muchas veces en el tiempo, de tal modo que compense el esfuerzo intelectual y computacional necesario para realizar la optimización con la posterior reducción de recursos para resolver los futuros problemas… incluso nuestro colega J ilustró en un comentario un ejemplo real en que optimizar no compensa. Ignoro si en este caso de las Cifras compensa o no, pero… ¿¡y lo bien que me lo paso…!? ¿Eh?
Bueno, al tajo.
En primer lugar, si lo que queremos es resolver un único problema concreto, desde luego que la aproximación adoptada por Antonio Villena en su estupenda página es mucho más coherente que la mía… pero decía yo que, ante la necesidad de resolver un problema dado, se puede atacar de dos modos: mirando la solución efectiva del problema concreto en sí, o buscando una solución completa para todos los problemas de su género. Y ponía yo un ejemplo: Supongamos que para construir no sé qué mecanismo tenemos que encontrar la integral de cierta función f(x) entre los puntos x=1 y x=2. Podemos resolver el problema de dos modos: bien analíticamente, bien estadísticamente.
Analíticamente: Buscamos cuál es la función integral de la función dada, por partes, por cambio de variable y todo eso, encontrando finalmente que la función integral de f(x) es, digamos, g(x). Ahora sustituimos x=1 y x=2 en g(x), hallamos la diferencia de los dos valores, y ya tenemos el valor pedido… el valor exacto. Pero en este caso hemos hecho más, mucho más que resolver nuestro problema concreto para x=1 y x=2… Hemos resuelto cualquier problema que implique encontrar la integral de esa misma f(x) entre cualesquiera puntos.
Si el proceso de encontrar esa g(x) fuera enormemente complejo,[2] estaríamos gastando grandes recursos para resolver una única integral que nos interesa: entre x=1 y x=2. A cambio, una vez obtenida dicha g(x), ya sabemos para siempre jamás cómo resolver todos los problemas de integrales de esa f(x) concreta.
Estadísticamente: Diseñamos un astuto aunque sencillísimo proceso informático en el que se define un paralelepípedo de área cuadrada, comprendida entre x=1 y x=2 (los valores de nuestro problema concreto), y los límites de las ordenadas y suficientemente grandes, por arriba y por abajo, como para contener todos los valores de la función ente esos puntos, digamos y1 e y2.
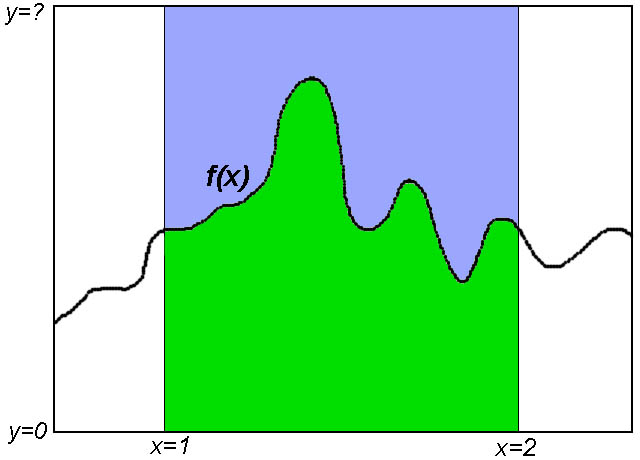
La cosa sería como en la imagen anterior. Nos fijamos en el paralelepípedo formado entre los puntos 1 y 2 del eje X y los puntos 0 y ? del eje Y, siendo ? el suficiente como para contener el valor más alto de f(x)… que es la curva sandunguera del medio.
Una vez hecho esto, se generan millones de puntos aleatorios comprendidos en dicho paralelepípedo y se “bombardea” con ellos el área rectangular definida por los puntos (1,y1), (2,y1), (1,y2) y (2,y2). Para cada punto generado, se calcula si dicho punto está por encima o por debajo de la función f(x), y vamos simplemente sumando cuántos caen dentro del área de la función y cuántos fuera…[3] Al terminar el proceso, si, por ejemplo, el 75% de los puntos han caído dentro de la función (la zona verde, que es la integral buscada, tiene el 75% de los puntos, mientras la zona azul tiene el 25% restante) y el área del paralelepípedo era de, digamos, dos metros cuadrados… pues el área comprendida por la función entre x=1 y x=2, es decir, la integral de dicha función entre los puntos 1 y 2, es de 1,5 metros cuadrados, el 75% del valor del área total. Sencillo. El valor no es completamente exacto, claro, pero si queremos más decimales de precisión, basta con bombardear más y más millones de puntos aleatorios…[4]
Esta aproximación estadística tiene la gran ventaja de que no necesitamos conocer para nada la función integral de la original, esa dichosa g(x) a que me refería antes (casos hay en que no es posible calcular analíticamente la función integral), para obtener un valor suficientemente preciso… pero el proceso es irrepetible: sólo sirve para ese caso concreto y nada más. Si mañana tenemos que calcular la integral de f(x), la misma función, digamos entre x=4 y x=6, no queda más remedio que volver a montar todo el tinglado otra vez.
.
¿Qué aproximación es la mejor? Pues… depende. Si pensamos que sólo vamos a tener que resolver cierto problema una única vez, no merece la pena (no suele merecer la pena, para ser exactos) hacer grandes optimizaciones. Ahora bien, si lo que queremos es empotrar el algoritmo en un micro, o ejecutar millones de veces diarias el programa, más vale que gastemos algo de tiempo en optimizarlo.
Evidentemente, mi aproximación al problema de Cifras y Letras, tal como vimos en los artículo dichosos, es analítica, y además es Universal, en el sentido de que no importa ni el orden de los argumentos ni sus valores ni nada de nada: el conjunto de fórmulas de millón y pico de registros es capaz de resolver cualquier cosa que le echemos con pinta de “Cifras y Letras”. En una palabra, no impone ninguna restricción a la forma de presentar el problema.
.
Entonces Antonio Villena planteó la siguiente cuestión: ¿Qué pasaría si ordenamos previamente, de menor a mayor, los números del problema? En este caso se podría eliminar un conjunto de fórmulas (en principio no sabemos cuántas), lo que aligeraría el proceso de cálculo de cada problema concreto, pero… ¿a cambio de qué?
Bien, lo primero que pasa es que la solución habría dejado de ser “Universal”. Estamos exigiendo al programa “llamador”, al demandante de fórmulas, que prepare los argumentos de una determinada manera, ordenados de menor a mayor, y si no se atiene a esa forma de entregar los parámetros entonces los resultados serán impredecibles.[5] Si se envían los argumentos sin ordenar, podría ser que la fórmula que resolviera el problema fuera una de las eliminadas al suponer que sí estaban ordenados, y el programa reportaría que no hay solución cuando sí que la hay.
Pero, por otra parte, si de esta manera el fichero tiene menos fórmulas, será más rápida la comprobación para cualquier problema dado y más sencillo empotrar el algoritmo donde sea. ¿Qué hacer? Dilemas, dilemas…
Como pasa casi siempre, cada caso tiene ventajas e inconvenientes. Vale, ordenar seis números de menor a mayor no parece un gran esfuerzo… una simple burbuja lo hace en un periquete, sin siquiera necesidad de usar algoritmos de ordenación más sofisticados. Es decir, no es lo que se tarda en ordenar el problema, lo es el hecho de que hay que hacerlo, que hay que acordarse de ordenar, de programar el algoritmo de ordenación, y gastar unos pocos ciclos de CPU en ordenar los números…
De acuerdo, ordenar seis números no es ni muy complicado ni muy costoso, a poco que ganemos es más que seguro que compensa ordenar… pero ahora hay que contrastar esta necesidad adicional con la posible ganancia de fórmulas que obtengamos. En caso de que ganemos cinco o seis mil fórmulas seguramente no merezca la pena complicarse la existencia, pero si ahorráramos 100.000 ó 200.000 fórmulas, un 10 o un 20%, la cosa cambia.[6]
No queda, pues, más remedio que meterse en harina y proseguir la optimización de fórmulas, a partir del fichero de fórmulas supuestamente perfecto de 1.025.472 registros, añadiendo como restricción adicional que los argumentos estén siempre ordenados, es decir, suponiendo que el argumento 1 es menor o igual que el 2, que a su vez es menor o igual que el 3… y así sucesivamente hasta el 5, que es menor o igual que el 6, que será por tanto mayor o igual que todos los demás. Si los números del problema son, por ejemplo, 7, 10, 1, 25, 8, 7, entonces antes de pasar la criba contra el fichero de fórmulas habría que ordenarlos, dejándolos así: 1, 7, 7, 8, 10, 25.
Es obvio que el fichero original del millón de fórmulas es capaz de resolver cualquier problema en que los argumentos estén ordenados de cualquier manera, dado que éste es un caso particular del Universal… que es que vengan como les dé en gana. Por tanto, la primera premisa se cumple: el fichero original sirve para resolver problemas formulados de esta forma especial. Entonces, lo que haremos será buscar qué fórmulas adicionales podemos eliminar debido a que los argumentos estén ordenados. De hecho, a partir de este momento, y en lo que queda de artículo, supondré que los argumentos vienen ordenados de esta manera. De forma fina, podemos decir que 1 ≤ 2 ≤ 3 ≤ 4 ≤ 5 ≤ 6.[7]
Ahora bien, si el fichero del millón y pico de fórmulas se supone que ya tiene todas las fórmulas sin redundancia alguna… ¿Qué más fórmulas podemos eliminar, entonces, gracias a la ordenación previa de los números del problema?
Recordemos que, como tanto los argumentos (los números dados) como el objetivo son números enteros y positivos, podemos descartar en la comprobación todas las fórmulas que, en cualquier momento de su desarrollo, obtengan un resultado parcial negativo o no entero. Esto ya lo discutimos en el segundo de los artículos; aquí lo daré por supuesto, y no voy a incidir más en ello. Estos descartes los podemos hacer en el proceso de resolución, cuando estamos leyendo el fichero de fórmulas y aplicándolas a resolver un problema concreto (vimos que, de media, ahorraba alrededor de un 47% de todas las operaciones posibles, que es mucho ahorrar)… pero no podíamos utilizar este hecho para eliminar fórmula alguna del fichero, pues los argumentos podrían ser cualquier número válido y sólo en tiempo de comprobación de unos números concretos podemos eliminar fórmulas… Es decir, es completamente imposible saber, por ejemplo, si la operación [41-] (en infix, [1-4]) dará o no un valor negativo, pues tanto el primer número dado como el cuarto, que son los involucrados en la resta, pueden tener cualquier valor de los permitidos en el concurso.
Pero si asumimos que los argumentos vienen ordenados siempre, esto cambia radicalmente: ahora que los argumentos siguen un patrón (estar ordenados de menor a mayor) sí que podemos aplicar este conocimiento previo para eliminar fórmulas que sabemos a priori que van a dar un resultado negativo, cero o no entero.
Un ejemplo ayudará a aclarar dudas: Sea una fórmula donde aparece en cualquier punto la cadena [63-] (como la [12x5+63-x4+], por ejemplo). En infix, este [63-] es (3-6), es decir, se calcularía directamente el tercer argumento menos el sexto, que luego se usaría para sumar, multiplicar o lo que sea con el resto de argumentos. Pero ahora sabemos que este argumento sexto es necesariamente mayor o igual que el tercero, pues vienen ordenados, por lo que podemos asegurar que esta operación [63-] bajo estas condiciones va a dar siempre un resultado negativo o cero. Siempre y en cualquier circunstancia. Es decir, en el proceso de comprobación, sea cual fuera la combinación de argumentos dados, cuando calculemos esta fórmula será siempre descartada sin remedio. Y esto ocurre para cualesquiera valores de los argumentos (siempre que estén ordenados, claro). Entonces, podemos descartarla de antemano, eliminándola definitivamente del fichero de fórmulas. Chao. Goodbye. Sayonara/Hasta la vista, baby.[8]
Éste será el argumento central de todo lo que sigue: descartar fórmulas que sepamos de antemano que siempre, bajo cualquier circunstancia y con cualquier valor de los argumentos, den cualquier resultado parcial o final negativo, cero o no entero. Suponiendo que los argumentos están ordenados, desde luego. Vale, sí, me estoy poniendo pesado… lo de que estén ordenados los argumentos de menor a mayor no lo voy a repetir más.
Vamos entonces, como ya hicimos en los otros artículos, a desgranar paso a paso qué y cuántas fórmulas del fichero reducido de 1.025.472 registros se pueden eliminar, y debido a qué.
.
Eliminación 1 (Operaciones simples)
En el caso de fórmulas con el patrón AB·, donde el operador (·) es (-) ó (÷), entonces eliminar la fórmula si el argumento A es mayor que el B. Este ejemplo ya lo hemos visto: ante un patrón “42/” en cualquier lugar de la fórmula, ésta se puede eliminar tranquilamente, pues al ser 2≤4[9] implica que su resultado será siempre menor o igual que 1. Si fuera una resta, como en [42-], lo mismo, pues el argumento 2 menos el 4 será siempre cero o negativo.
Aquí se podría pensar (yo lo pensé inicialmente) que no se puede eliminar alegremente en caso de división, porque quizá sean los argumentos 2 y 4 iguales (entonces lo sería también el tercero, claro), en cuyo caso su división es 1, que sí es un resultado válido… pero, claro, en el conjunto de fórmulas debe, tiene que estar también la fórmula idéntica pero donde se hace [24/] en lugar de [42/], que en este caso también daría 1… y cumpliría la misma función, llegando al mismo resultado. Que se puede eliminar, vaya.
Bien, aplicando exclusivamente esta transformación al fichero original del millón y pico de fórmulas se eliminan… ¡393.840 fórmulas, nada menos! … ¡un 38,4% de las fórmulas reducidas! En realidad se eliminarían 207.495 fórmulas por tener una resta con argumentos desordenados, y otras tantas por tener una división… pero algunas fórmulas contienen ambas configuraciones, en concreto 21.150, por lo que la reducción es menor. Pero es muy grande de todos modos, así que vamos a seguir investigando, a ver qué más encontramos…
.
Eliminación 2 (Caso general)
En el caso de fórmulas con el patrón A·, siendo el operador (·) una resta o división, eliminar la fórmula si el término anterior al “A” sólo consta de sumas y/o multiplicaciones, siempre que alguno de sus términos sea mayor que el argumento A. Así, sólo con la definición, desde luego que no se ve muy claro, así que toca explicarlo. Cuando encontramos un patrón A- (o A÷, igual da), significa que en la pila existe un cierto valor resultado de una serie de operaciones anteriores, término que será restado de/dividido por el término A. Veamos un ejemplo:
Sea la fórmula [15+2-] (en infix, [2-(1+5)]). En este caso nos fijamos en la configuración final, [2-]: un operador (-) y un argumento 2, que es el minuendo de la resta. El segundo operando de la resta, el sustraendo, es en este caso la fórmula [15+]. Este sustraendo es el resultado de sumar dos argumentos (1 y 5),suma que, debido a las condiciones del problema, dará necesariamente un resultado mayor o igual que el mayor de todos los argumentos involucrados, en este caso el 5. En caso de ser sumas, el resultado sería estrictamente mayor que el mayor de los argumentos; en caso de productos, podría ser igual también: por eso digo “mayor o igual”. Por lo tanto, la operación (-) restará del argumento 2 un valor, resultado de [15+] que es necesariamente mayor o igual que el mayor de sus argumentos, el 5, que, al estar ordenados, es a su vez mayor o igual que el minuendo, el argumento 2… El resultado de la operación es, por tanto, en todo caso menor o igual que cero si es una resta, o bien menor o igual que 1, si es una división. Si en el proceso de resolución intentamos comprobar esta fórmula, será descartada, siempre y para cualquier valor de los argumentos (¡ordenados!), así que podemos ahorrárnosla. La fórmula se puede eliminar.
Esta eliminación afecta a fórmulas de cualquier tamaño, no sólo fórmulas sencillas como las del ejemplo anterior. Así, también eliminaría, por ejemplo, la fórmula [15+26x4+x3-], que en infix sería: [3-(1+5)x( (2x6)+4 )]; dado que todos los argumentos del sustraendo están sumando o multiplicándose entre sí, y al menos uno de ellos (tres en este caso: el 4, el 5 y el 6) es mayor o igual que el minuendo (3), el resultado final de la formula será necesariamente menor o igual que cero, y se puede eliminar a priori. Naturalmente, como os habréis dado cuenta cabal, esta eliminación incluye a la Eliminación 1, pero las mantenemos separadas por claridad en la exposición (¡o al menos eso espero!).
Nuevamente estamos ante una potente eliminación, pues aplicada al fichero original eliminaría 511.888 fórmulas, es decir, 118.048 fórmulas adicionales a las que ya conseguía la eliminación 1… ¡prácticamente la mitad de todas las formulas! Quedaría un fichero de tan sólo 513.584 fórmulas. Esto ya sería suficiente para quedarse con estas mejoras al proceso… ahorrarse casi la mitad de las fórmulas parece una más que suficiente compensación por tener que clasificar previamente los argumentos… pero ya que estamos en esta tesitura de optimizar sin tasa ni mesura, sigamos pensando a ver qué más podíamos eliminar.
.
Eliminación 3
Aquellas fórmulas con un operador (·) que sea una resta o división, siempre que aplique a dos términos compuestos, eliminar la fórmula si todas las operaciones de cada uno de los dos términos son o sumas o multiplicaciones, pero todas ellas iguales, y todos los operandos del primer término son mayores, uno a uno, que los operandos equivalentes del segundo término. Uff, si la anterior se entendía poco, ésta aún menos…También toca explicarlo.
Sea una fórmula que contiene la secuencia [46x15x-] (en infix, [(1x5)-(4x6)]), que es una fórmula “autocontenida”, en el sentido de que su resultado es un único número. Sabemos, porque están ordenados, que ambos argumentos 1 y 5 son menores o iguales, uno a uno, que los argumentos 4 y 6. Es decir, 1 es menor o igual que 4, y 5 menor o igual que 6. Por tanto, sus productos (o sus sumas, tanto da) también mantienen la misma relación: (1×5) es necesariamente menor o igual que (4×6), de la misma manera que (1+5) es menor o igual que (4+6). La consecuencia es que la operación de resta de ambos términos dará siempre un resultado negativo o cero (y si fuese una división, menor o igual que uno). Podemos eliminarla, pues, con toda tranquilidad.
Nótese que es necesario que todos los operadores de ambos términos sean iguales, pues si se mezclaran sumas con multiplicaciones podríamos fácilmente construir un contraejemplo. Nótese también que es necesario que cada argumento del sustraendo sea menor que el equivalente del minuendo, y nótese, por fin, que esta última circunstancia obliga, para poder aplicar esta eliminación, a que la fórmula cumpla una condición adicional: que el término sustraendo tenga como mínimo el mismo número de operandos que el término minuendo, pues si tuviera más operandos podría hallarse con facilidad un contraejemplo. Sería el caso siguiente: [56+234++-], que en infix es [(2+3+4)-(5+6)]. Suponiendo que los argumentos fueran, por ejemplo, [1, 5, 6, 7, 8, 8], esta fórmula sería: (5+6+7)-(8+8)… fórmula que da el resultado 2, un valor perfectamente válido. Por tanto, el minuendo tiene que tener como máximo el mismo número de términos que el sustraendo, y lo mismo aplica sobre el dividendo y el divisor.
El caso es que aplicando exclusivamente esta eliminación, con todas sus restricciones, se eliminan 4.496 fórmulas, que quizá no es mucho, pero prácticamente todas ellas son adicionales a las ya eliminadas: el fichero resultante hasta aquí tiene ya tan solo 509.448 fórmulas. Ya hemos cruzado el ecuador: hemos eliminado más de la mitad de los registros originales. ¿Se puede hacer algo más? Sí, se puede. A ver cómo podemos atornillar un poco más nuestro fichero…
.
Eliminación 4
En el caso de fórmulas con el patrón ABC··, donde los dos operadores (··) son restas (-) o divisiones (÷) en cualquier orden, y el operando A es mayor que B y que C, eliminarlas. Ésta es más sencilla de ver, creo yo.
Sea, por ejemplo, la fórmula [531-/], que en infix sería [(3-1)÷5][10] Al ser el dividendo una resta entre dos argumentos menores o iguales que el divisor, el resultado es obligatoriamente menor o igual que uno (en este caso concreto, estrictamente menor), o si el último operador es una resta, el resultado sería menor o igual que cero… podemos descartarla, en cualquier caso.
Aplicando esta eliminación al fichero original eliminaríamos 40.720 fórmulas… la mala noticia es que muchas de ellas serían también eliminadas por pasos anteriores, sólo 17.260 son nuevas eliminaciones. El fichero quedaría, hasta aquí, con 492.188 registros. Veamos si podemos explotar este tipo de fórmulas un poco más…
.
Eliminación 5
En el caso de fórmulas con uno de los patrones siguientes: ABCD···, ABC·D··, ABCDE····, ABCD·E···, ABC·DE···, ABC·D·E··; donde todos los operadores (·) son restas (-) o divisiones (÷), en cualquier orden, y el operando A es mayor que B, que C, que D y, eventualmente, que E, eliminarlas. En realidad es aplicar el mismo principio que en el caso anterior, pero a fórmulas con más operandos (tres o cuatro; para cinco no es necesario porque sabemos desde el principio de los tiempos que las fórmulas cuyos operadores sean todas restas o divisiones no están, de antemano, en el fichero), así que me ahorro la explicación.
El caso es que aplicando simultáneamente esta eliminación con la anterior, se eliminarían 48.256 fórmulas, 7.536 adicionales a la Eliminación 5, pero nuevamente muchas de ellas son también reducidas por otras eliminaciones, así que la ganancia total en este caso es de otras 3.546 fórmulas, quedando un fichero de fórmulas de 488.642 registros. Únicamente un 47% de las fórmulas originales del fichero sin redundancias… que, si no he hecho algo mal, resuelven los mismos problemas que el fichero original de millón y pico.
Y sí, habéis adivinado, si he puesto el número de registros en negrita es porque hasta aquí llego. Ya no se me ocurre cómo buscar más maneras de eliminar fórmulas, por mucho que los argumentos estén ordenados. Igual en los comentarios a alguno de vosotros se le ocurre algún truco más; si lo hacéis, yo lo pruebo, a ver qué pasaría…
Un apunte: Si os acordáis de lo que contaba en aquellos artículos, debido a que en cuanto se detecta un valor negativo, cero o no entero se para el proceso de esa fórmula, resulta que, revisando el fichero del millón de fórmulas, sólo había que hacer, de media, un 53% de las operaciones que serían necesarias sin hacer esta comprobación. Como ahora hemos eliminado a priori muchas de estas fórmulas, es evidente que no habrá tanto descarte a la hora de resolver combinaciones, y serán precisas más operaciones, en media, para hacerlo. ¿Cuánto? Pues ahora, con este nuevo fichero de 488.642 combinaciones es preciso realizar alrededor del 69% del total de operaciones posibles. Un ahorro de sólo un 31%, en vez del 47% de antes… Pero como tenemos menos de la mitad de fórmulas que comprobar, la ganancia es evidente, me parece a mí.
En el fichero hay 569.121 sumas y otras tantas multiplicaciones, pero 652.484 restas y divisiones, debido al carácter no conmutativo de éstas últimas. Y esta vez el número de registros, ese 488.642, tiene una descomposición en factores primos bastante curiosa: 2, 7, 11, 19 y 167. No sé si querrá decir algo o qué, pero que sean cinco factores primos diferentes ya es raro, me parece a mí.
.
En fin, hasta aquí el proceso. Sólo me queda una duda… Una duda gorda: ¿De verdad todo esto ha servido para algo? En una palabra, ¿será el nuevo fichero realmente equivalente al original?, o quizás ¿me habré cargado alguna fórmula que sea necesaria para resolver algún problema concreto? Hemos reducido casi un 53% las fórmulas necesarias, que es mucho reducir, a cambio del pequeño esfuerzo de ordenar siempre los argumentos antes de comprobarlos con el fichero, pero, ¿de verdad el fichero sigue siendo válido? En principio las eliminaciones parecen irreprochables, pero a mí eso no me sirve. Tengo que comprobarlo, tengo que asegurarme, tengo que probar… ¿Se nota que soy un informático del tiempo de Amenofis IV? Así que… a ello me puse.
En primer lugar hice lo que hice tiempo atrás para comprobar la validez del fichero original, el de 1.025.472 registros, es decir, generar decenas de miles de casos aleatorios y comprobarlos con el nuevo fichero. En los casos en que no se encuentre solución, trato entonces de resolverlos usando el fichero del millón (que ya he dado por bueno; hacerlo así es incomparablemente más rápido que hacerlo por fuerza bruta), y si alguno sí que tiene solución, apuntarlo. Tras algún centenar de miles de pasadas, no encontré ninguno.
Pero esta vez no me encuentro seguro. Necesito más… Así que programé un largo y tedioso procedimiento por el que generaba todas y cada una de las posibles combinaciones de argumentos ordenados y las comprobaba con todos y cada uno de los objetivos posibles, del 101 al 999. Una burrada. Un problema NP-pesado, en definitiva. Muy pesado.
Antonio Villena nos ilustró en el segundo artículo, en su comentario número 26, sobre cómo calcular cuántas combinaciones posibles de catorce argumentos ordenados[11] son posibles: 27.132 (cosa que yo, muchísimo mas torpe con la combinatoria, había ya deducido de la única manera que sé: escribiendo un programa y contándolas). Como los posibles objetivos van del 101 al 999, son 899 posibles, que multiplicados por las 27.132 formas de entregar los argumentos dan… mucho. Veinticuatro millones y pico de combinaciones. Pero como todo el trabajo en realidad no lo tenía que hacer yo, humilde humano de limitadísima inteligencia, sino el ordenador, que no deja de ser una máquina de paciencia infinita que ni se aburre ni se cansa mientras no le falte la electricidad, se trataba de tenerle funcionando día y noche. Y día… Y noche… Y más días… Y más noches…
.
El caso es que tras tan ingente y probablemente inútil trabajo resulta que he comprobado fehacientemente que todas y cada una de las combinaciones de números y objetivos posibles que no tienen solución revisando el fichero reducido de 488.642 fórmulas, tampoco la tienen revisando el fichero original del millón y pico. Para mayor seguridad, también he revisado algunos números objetivo concretos, cinco o seis diferentes, unos altos y otros bajos, por fuerza bruta. Y el resultado fue el mismo: Ninguna incoherencia. El fichero es correcto, pues.
Aquellos que, por alguna oscura razón, tengan interés en el fichero resultante de tanto esfuerzo, aquí pueden descargárselo, libre de derechos de autor. Está comprimido y ocupa poco más de un Mb.
.
Y claro, tras semejante esfuerzo, resulta que ahora sí puedo contar algunas curiosidades sobre qué combinaciones de números tienen más o menos probabilidades de llegar a cualquier solución, o qué objetivos resultan más fáciles o difíciles de obtener con las diferentes combinaciones de números. Dije en el segundo de los artículos que, empíricamente, el número de problemas sin solución era algo superior al 9%. En realidad es el 19,3%. 4.713.199 combinaciones de las 24.391.668 totales[12] no tienen solución. La razón de tal discordancia es que en la generación aleatoria de problemas a que hice referencia entonces tenía en cuenta una restricción que se da en el concurso: que no haya más de dos números de dos o más cifras, mientras que ahora no hay restricción alguna. Esta distinción aparentemente tan tonta hace que el número de problemas sin solución se duplique con creces.
Por otra parte, hay una serie de combinaciones de cifras, exactamente 51, que son posibles, pero que no alcanzan a obtener ningún objetivo comprendido entre 101 y 999, ni uno solo. Por ejemplo la [1,1,2,2,2,5], con la que el mayor número que puede construirse es 90, menor que cualquiera válido.
Descartando estas 51 combinaciones imposibles, quedan 27.081, es decir, la gran mayoría, que sí son capaces de llegar al menos a un posible objetivo. Lógicamente, las combinaciones con números muy bajos o muy altos alcanzan muchos menos posibles objetivos que combinaciones con números variados, con algunos altos y también bajos. Así, la combinación [1,1,2,2,3,4] sólo alcanza a un único objetivo, que es el 108 (hay en total 13 combinaciones que son susceptibles de alcanzar solamente un único objetivo de los 899 posibles), y hay una única combinación que alcanza exactamente a dos objetivos, la [1,1,1,1,4,7], con la que podemos construir el 105 y el 112 y nada más.
Por el otro lado, la combinación [1,5,6,7,50,100] es capaz de componer todos los objetivos menos uno, uno solo (en este caso es el 824), y lo mismo le ocurre a otras 614 combinaciones de números, con las que podemos llegar a todos los objetivos menos a uno, distinto cada vez. Por fin, con la combinación [1,2,6,7,10,75], por ejemplo, podemos llegar a cualquier objetivo posible, pues alcanza para componer todos los 899 posibles objetivos entre 101 y 999. Y no es ella sola, hay exactamente 1.242 combinaciones de números, algo más del 4,5% de todas las posibles, que son capaces de componer los 899 objetivos válidos.
Una combinación “media” (si es que eso existe) alcanza para componer 725 objetivos de los 899 posibles,[13] un valor para mí sorprendentemente alto, con una desviación típica de 197. 4.597 combinaciones, nada menos que el 17% del total, sirven para componer 890 o más objetivos posibles (el primer percentil), mientras que sólo 85 combinaciones son capaces de alcanzar a nueve o menos objetivos de los 899 posibles (el último percentil). La mediana está en 801 objetivos posibles. Y el valor más repetido es, precisamente, 899, la totalidad: 1.242 combinaciones que son capaces de llegar a todos y cada uno de los posibles objetivos, siendo el segundo el 898, uno menos, con 615 combinaciones, y el tercero el 897, dos menos, con 491.
Más curiosidades: la combinación más alta, compuesta por seis números “100”, consigue llegar hasta 23 objetivos válidos,[14] y de las combinaciones con todos sus números iguales, la que consigue llegar a más objetivos es la compuesta por todos seises, que compone hasta 81 objetivos válidos, y la que menos, la de todos cincuentas, que sólo alcanza a componer 14 (descontadas las de todos unos y todos doses, que no llegan a ninguno, claro).
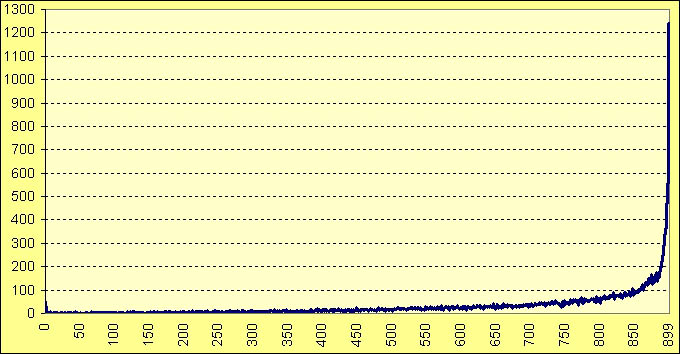
En la siguiente gráfica se pueden ver, en abscisas, a cuántos objetivos es capaz de llegar una determinada combinación (de 0 a 899), y en ordenadas, cuántas combinaciones de las 27.132 posibles son las que llegan a ese número de objetivos. Se ve un pequeño pico en el cero (las 51 combinaciones que no llegan a ningún objetivo), y luego la curva va subiendo lentamente, con alguna fluctuación poco importante, hasta más o menos 850 objetivos (momento donde se rebasa el número de 100 combinaciones que alcanzan ese número de objetivos), desde donde crece rapidísimamente hasta llegar a las 1.242 combinaciones que son capaces de alcanzar todos los 899 objetivos posibles.
.
¿Y en cuanto a los objetivos? Evidentemente, a los números objetivos bajos, por debajo del 200, se llega muy fácilmente, habiendo pocas combinaciones de cifras que no lleguen al resultado correcto, y lo mismo ocurre con aquellos números que se puedan obtener con un único par de números, como el 107, el 400 o el 675, por ejemplo. Así, sólo hay 159 combinaciones (descartadas las 51 que no obtienen ningún resultado válido) que no alcancen a componer el número 150, que es el más fácil de obtener de todos los posibles (26.922 combinaciones de las 27.132 posibles lo alcanzan), o las 213 que no llegan para componer el 102, el segundo más fácil de obtener de todos.
En el otro lado están, obviamente, aquellos objetivos que necesiten no menos de cuatro números para obtenerlos, y cuanto más altos, más difíciles. Si el objetivo que te cae en suerte es el 967, el más difícil de todos, son nada menos que 12.809 combinaciones las que no sirven, un 47% del total, descartando las 51 que son inútiles por no alcanzar ningún objetivo.
Por otra parte, cuando los objetivos resultan ser números primos es más difícil alcanzarlos: de los 30 objetivos que menos combinaciones alcanzan, nada menos que 19 son primos, entre ellos el dichoso 967, y de los que no lo son, uno de ellos es el 961, que como es 31 al cuadrado, es casi, casi como otro primo. Además, sólo uno de esos 30 más difíciles, el 787 (que sí es primo) es inferior a 850… si te toca un número alto y encima es primo, lo llevas crudo, amigo.
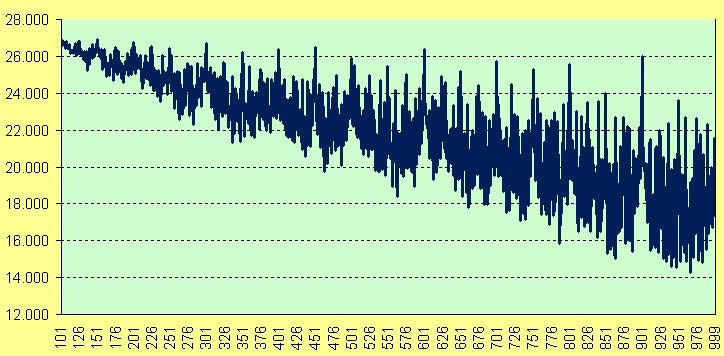
En la gráfica siguiente se puede observar cómo el número de combinaciones eficaces va disminuyendo conforme aumenta el objetivo, con repuntes puntuales debidos a esos números sencillos de componer, como el 900 o el 750, por ejemplo: se notan perfectamente los picos debidos a estos números sencillos. En abscisas, el número objetivo concreto, de 101 a 899, y en ordenadas, el número de combinaciones que son capaces de llegar a él.
.
Una última curiosidad: Revisando (por encima, claro) las combinaciones con o sin solución que se generaban, he encontrado algunos problemas que, pareciendo imposibles a simple vista, sí que tienen solución… os dejo un par de ellos para que penséis un poco si os place… en unos días, en comentarios, os daré la solución. Estos son:
Números: 4, 4, 4, 100, 100, 100. Objetivo: 550.
Números: 75, 75, 100, 100, 100, 100. Objetivo: 307.
.
Y hasta aquí este largo y pesado artículo/estudio/tostón sobre las Cifras dichosas, que cada cual se quede con la descripción que mejor le parezca.
Si a alguien se le ocurre cómo mejorar el proceso, cómo eliminar más fórmulas, cómo hacer todo el proceso más rápido, que lo diga en comentarios e intentaré comprobarlo.[15] ¡A lo mejor nos ganamos el millón de dólares por resolver este problema del milenio! Si me lo dan, ![]() , lo reparto entre los lectores de El Tamiz… Entre tanto, hasta aquí ha llegado este tercer artículo del descabellado estudio del problema de las cifras de Cifras y Letras.
, lo reparto entre los lectores de El Tamiz… Entre tanto, hasta aquí ha llegado este tercer artículo del descabellado estudio del problema de las cifras de Cifras y Letras.
Disfrutad de la vida, mientras podáis.
Y os dejen.
- Que no deja de ser un ataque por fuerza bruta, pero mucho más sofisticado. [↩]
- Para mí, ejem, siempre lo sería… tengo ligeramente olvidadas las integrales y tal… [↩]
- Para ello, se calcula el valor de f(x) para ese valor de x concreto, y se compara el valor obtenido (la y) con el valor de y del punto aleatorio. [↩]
- Existen problemas en que esta solución tampoco es usable, porque involucran funciones discontinuas con valores infinitos en el rango a integrar, como por ejemplo la delta de Dirac, pero escapan a lo que queremos ejemplarizar. [↩]
- Resultados impredecibles: Forma fina que los informáticos usamos mucho cuando lo que queremos decir en realidad es que “No funcionará ni harto de vino”. [↩]
- Ordenar seis números es sencillísimo, como es obvio, por lo que aparentemente con ganar unas pocas fórmulas ya compensaría… pero si nuestro fichero de fórmulas resultante es susceptible de ser usado por muchos otros, por ejemplo porque sea incluido en multitud de programitas de terceros, entonces sólo en caso de una ganancia sustancial merece la pena complicar la vida a todos esos terceros. [↩]
- ¿Tendré que decir aquí una vez más que 1, 2, etc, no son los números 1, 2 y compañía, sino que hacen referencia al primer número del problema, al segundo, etc?? Bueno, vale, lo digo. Por última vez. O casi. [↩]
- Tómese la versión que más le guste a cada cual. [↩]
- Como siempre, aquí “4” quiere decir “el cuarto argumento” y así sucesivamente, no es un número de valor 4. Esto ya lo dije como siete veces en los dos artículos anteriores y alguna más en éste; tras decirlo en esta nota al pie, ya no lo repetiré más veces. [↩]
- No tendré que recordar una vez más que aquí 1, 2, etc se refieren a los argumentos primero, segundo, etc, ¿no?, y que además están ordenados de menor a mayor. [↩]
- Los números del problema sólo pueden ser del 1 al 10, 25, 50, 75 ó 100. [↩]
- 27.132 combinaciones de cifras por 899 posibles objetivos. [↩]
- La combinación [1,1,3,8,8,50], por ejemplo, sería una combinación media prototípica, pues es capaz de llegar exactamente a 725 objetivos diferentes, junto con otras 46 combinaciones más. [↩]
- Del 101 al 104, el 150, del 197 al 203, el 250, del 298 al 302, del 399 al 401, el 500 y el 600. En total, 23. [↩]
- Lo del backtracking ya lo dijo, y lo programó, Antonio Villena, así que no vale. [↩]

The Resolviendo “Cifras y Letras” (y… III?) by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.




{ 10 } Comentarios
He conseguido el objetivo, aunque he necesitado más tiempo del que dan en el programa
Yo creo que el primer articulo estuvo bien, el segundo ya fue para enfermos y este ya empieza a ser demencial. La verdad es que nos dejas en nuestro sitio Yo creo que no deberias pedir consejos para sumergirse mas en el abismo de la locura, ¡nos arrastaras contigo! Y lo digo desde el cariño teniendo en cuenta que me ha gustado un monton las curiosidades, que haya tantos que consigan todos es impresionante y los numeros de en medio sencillos de componer es normal teniendo en cuenta que los valores altos de por ahi son multiplos de 5, ¿que pasaria si solo consideramos los numeros del 1 al 10?
Yo creo que no deberias pedir consejos para sumergirse mas en el abismo de la locura, ¡nos arrastaras contigo! Y lo digo desde el cariño teniendo en cuenta que me ha gustado un monton las curiosidades, que haya tantos que consigan todos es impresionante y los numeros de en medio sencillos de componer es normal teniendo en cuenta que los valores altos de por ahi son multiplos de 5, ¿que pasaria si solo consideramos los numeros del 1 al 10?
Y se me olvido, pero vamos, que para integrar hay otra forma que no planteas y que es la numerica. Aunque bueno, supongo que no la explicas por que tal vez no tenga relacion por el tema, pero me resulta extraña no verla por que viene a ser la de los ordenadores. No se si esa forma equivaldria ha hacer el basto, pero en fin, esta consiste en dividir la distancia en pequeños intervalos, supongamos cuatro. Hariamos cuadraditos con el valor medio de cada intervalo (no un medio complicado, la media entre el valor de la funcion en los dos extremos del intervalo) y sumariamos las cuatro areas.
En mi opinion creo que tu analisis anterior seria mas bien de este tipo, numerico, una aproximacion medio basta pero bastante rapida, la estadistica seria lo que decias de hacer a lo bruto con todas las formulas a la vez y con esta ya estariamos tirando a la analitica. Claro que quiza lo este interpretando al reves. Si el ordenador cuesta poco y los informaticos cuestan mucho, cuanto mejores sean los ordenadores, menos seran necesarios analisis asi. Me han comentado ingenieros del pleistoceno (y lo digo con cariño) sobre tablas de logaritmos y reglas super complejas que ahora con una calculadora de dos duros nos parecen absurdas. Pero bueno, cada cual lo vera como quiera. Como consuelo, en mi caso aun trabajo con procesos que dejan los ordenadores al nivel de latas de sardinas (o abacos para quien sepa que son) asi que tenemos que pensar mucho. Sera distinto cuando eso deje de pasar y todos no seamos mas que informaticos bastos, que le metamos mosntruosidades a los ordenadores por que lo resuelven miles de veces mas rapido de lo que tardariamos en optimizarlos, somos un especie en extincion.
Gracias por el artículo y por las numerosas alusiones que me has hecho ) Éste es el artículo que echaba en falta, con gráficas, estadísticas y curiosidades. Supongo que ha sido un trabajo que ha requerido gran esfuerzo mental y computacional.
) Éste es el artículo que echaba en falta, con gráficas, estadísticas y curiosidades. Supongo que ha sido un trabajo que ha requerido gran esfuerzo mental y computacional.
Igual con un cluster de Google se hace en cero coma dos, pero con un ordenador mundano te habrá llevado semanas.
@Antonio: Bueno, las alusiones son porque fuiste tú quien me metió en este lío… y sí, han sido semanas. Pero yo no hacía casi nada: sólo asegurarme que los vatios siguieran llegando…
La verdad es que me lo he pasado muy bien pensando un poco más.
@Sergio B: ¡No te metas con las tablas de logaritmos ni con las reglas de cálculo, que yo fui usuario!!! Menudas eran, las tablas de logaritmos… Como curiosidad, te diré que mi (seguramente) primer programa funcional en Primero de Carrera servía para imprimir… ¡Una tabla de logaritmos! Qué tiempos!!
Qué tiempos!!
Oye @Macluskey, me haz dejado con la duda, ¿qué es eso de tabla de logaritmos?. He buscado con Google por Internet pero sólo me salen las tablas, sin explicaciones de cómo se usa o para que sirve, ¿podrías darnos una luz acerca de esto?
Joder, qué viejo me siento… le dejo a Mac que lo explique, pero yo también las utilicé en el colegio, sospecho que por tradición más que por otra cosa
@Helq: Caramba, difícil cuestión… no porque sea difícil, sino porque casi no me acuerdo…
A ver: las tablas de logaritmos eran unos libros similares a dietarios, en los que venían, que yo recuerde, tres tipos de datos: los logaritmos de los números del 1 al 10.000, los de los senos de 0 a 90º cada minuto de arco, y lo mismo con los cosenos. Todos los logaritmos venían con lo menos 6 decimales, incluso es posible que más. En algunas venían además los logaritmos neperianos, pero no en las mías, que eran de pobre…
¿Cómo se usaban? Fácil. Por ejemplo querías multiplicar 8.564 por 35.451. Recuerda: No hay calculadoras, ni tampoco Excel, ni nada de nada. Sólo papel, lápiz y tus tablas de logaritmos.
Lo que sabías es que log(8.564)+log(35.451)=log(8.564×35.451).
Entonces ibas a tu tabla, buscabas el log de 8564 y encontrabas que era 3,932677. Lo anotabas.
Luego buscabas el log de 35.451. No estaba, porque sólo llegaba al 10.000. No importaba: buscabas el log de 3.545 y veías que era 3,549616. Así que el logaritmo de 35.451 debía ser 4,549616 y… un pelín más (porque ése es el logaritmo de 35.450, claro, no el de 35.451) (no me mires con esa carita: el logaritmo de “10x” es el “logaritmo de x” + 1… ésa era la gracia de los logaritmos) , así que ponías, por ejemplo, 4,549625.
Ahora sumabas ambos valores: 3,932677 + 4,549625, y daba 8,482302.
Ahora ibas a la tabla de logaritmos a buscar quién era el número cuyo logaritmo fuera 8,482302… o mejor, 0,8482302, que era como de verdad venía. Ese número es 3036. En realidad sería un poquitín más (porque la cifra buscada 0,482302 no venía exacta, claro), así que ponías 3.036,02, por ejemplo. Como el exponente de tu logaritmo era “8″, eso quiere decir que la cifra buscada tiene 9 cifras por delante del punto decimal… así que no es 3036 el resultado buscado, sino más bien 303.602.000. Ése es el resultado.
No es exacto-exacto, claro, pero, para la gran mayoría de necesidades usuales, te da igual que el resultado sea 303.602.000 que 303.602.364, que es lo que da de verdad la multiplicación.
Y todavía para multiplicar… puede tener su utilidad, pero sólo te quita una multiplicación. Ahora bien, para exponenciar… si tenías que hacer 3567 elevado a 3,45, ahí ya la cosa se ponía fea.
Y con logaritmos era igual de sencillo: buscabas el logaritmo de 3567, lo multiplicabas por 3,45, hallabas el antilogaritmo (el número cuyo logaritmo da el que tienes), y listo. Con un montón de error, pero las cinco o seis primeras cifras del resultado las clavabas… Sufi.
¡¡Qué reviejo que es uno, que aún se acuerda de estas cosas…!!
Espero que haya servido….
Mac
Ahhhhh, ya veo. Pues debía ser muy útil para hacer las cosas rápido, porque es mucho mejor hacer una multiplicación directa . Pero hacer de forma directa una exponencial debía ser de lo peor, y en ese caso te doy la razón en usar las tablas. Muchas gracias, detallitos históricos de lo que uno se entera en lugares que no se esperan, Grande el cedazo, tamiz, y todos sus colaboradores… y claro a Pedro
. Pero hacer de forma directa una exponencial debía ser de lo peor, y en ese caso te doy la razón en usar las tablas. Muchas gracias, detallitos históricos de lo que uno se entera en lugares que no se esperan, Grande el cedazo, tamiz, y todos sus colaboradores… y claro a Pedro 
Yo también usé las famosas tablas….. snif, que nostalgia
Escribe un comentario