Por tercera semana consecutiva seguimos enzarzados en la serie Cuántica sin fórmulas, tratando de desentrañar los secretos de los estados cuánticos. Hace dos semanas hablamos acerca del concepto de estado cuántico, y la semana pasada lo hicimos sobre un tipo de estados especiales: los eigenestados, estados propios o autoestados de un observable determinado. Como espero que recuerdes, una de las propiedades fundamentales de los autoestados era que se trataba de lo que llamamos “estados incompatibles”. Como dije entonces, esta propiedad proporciona a los autoestados una enorme potencia para describir cualquier otro estado cuántico del sistema (al menos, en lo que se refiere al observable al que describen). Hoy nos centraremos precisamente en esto, y trataremos de escribir cualquier estado de nuestra “moneda cuántica” en función de sus estados propios utilizando, por supuesto, la elegante notación bra-ket de Dirac. Hablaremos sobre las superposiciones cuánticas, utilizando las mismas simplificaciones abyectas de los artículos anteriores.

La cara de Cthulhu tras enfrentarse a los espacios de Hilbert. Crédito: Wikipedia/FDL.
Para empezar, debemos profundizar algo más en el concepto de “estados incompatibles”, puesto que si no conoces cálculo vectorial –y no parto de la base de que lo conozcas– no es sencillo entender las implicaciones del hecho de que, por ejemplo, $\left \langle cara | cruz \right \rangle = 0$. Naturalmente, de lo que sí parto es de que entiendes la expresión que acabo de escribir; si no es así, mejor retrocedes a los artículos anteriores.
Los dos eigenestados de la moneda, $\left | cara \right \rangle$ y $\left | cruz \right \rangle$, establecen las dos únicas posibilidades que pueden medirse del observable lado de la moneda; cualquier otro estado se “colapsa” a uno de estos dos estados una vez que observamos la moneda. Es más: cualquier estado anterior, como vimos en las entradas anteriores, viene a ser una medida de la probabilidad de que, al observar la moneda, su estado sea $\left | cara \right \rangle$ o $\left | cruz \right \rangle$.
Es como si cualquier estado pudiera ser “completamente $\left | cara \right \rangle$”, “completamente $\left | cruz \right \rangle$”, o una combinación de los dos: “casi completamente $\left | cara \right \rangle$ y un poquito $\left | cruz \right \rangle$”, “prácticamente $\left | cara \right \rangle$ pero un poco $\left | cruz \right \rangle$”, “medio $\left | cara \right \rangle$ y medio $\left | cruz \right \rangle$”, etc. Es decir, puede pensarse en los estados de la moneda como superposiciones de los dos autoestados. Esto es posible, precisamente, por la “estúpida propiedad” que mencionamos en el artículo anterior: la incompatibilidad de los dos estados o, matemáticamente, por la perpendicularidad entre los dos autoestados .
Una manera bastante visual de representar las posibilidades del estado de la moneda es utilizar coordenadas espaciales: esto requiere cierta imaginación y que te abstraigas, pues no son coordenadas espaciales del espacio euclidiano. Imagina que dibujamos dos ejes: voy a llamar al eje horizontal “eje cara” y al eje vertical “eje cruz”. Ambos ejes van de 0 a 1 (porque, si sabes algo de cuántica, como hicimos en la entrada anterior suponemos que los estados están normalizados y ese 1 significa “100%”), con lo que al final, tenemos un cuadrado de lado 1 como éste, en el que el origen –el punto $(0,0)$– está en la esquina inferior izquierda:

Mi intención es ahora convencerte de que podemos representar cualquier estado posible de la moneda en ese cuadrado. Empecemos por los dos más evidentes: el estado $\left | cara \right \rangle$ está puramente sobre el “eje cara” horizontal, y no tiene absolutamente nada de “cruz”, con lo que sus coordenadas en nuestro cuadrado serían $(1,0)$, y en el dibujo se encuentra aquí:

Lo mismo sucede con el otro autoestado, $\left | cruz \right \rangle$: en este caso, por supuesto, sucede al contrario. No tiene nada de “horizontal” (cara) y es completamente “vertical” (cruz), de modo que sus coordenadas en nuestro cuadrado son $(0,1)$:

Cualquier otro estado de la moneda puede dibujarse como un punto dentro del cuadrado, pero ¡ojo!, es fundamental que entiendas este breve párrafo para comprender realmente la naturaleza de nuestra representación de estados en función de $\left | cara \right \rangle$ y $\left | cruz \right \rangle$: todos los estados posibles son puntos dentro del cuadrado, pero no todos los puntos del cuadrado son estados posibles.
Por ejemplo, fíjate en el punto $(1,1)$:
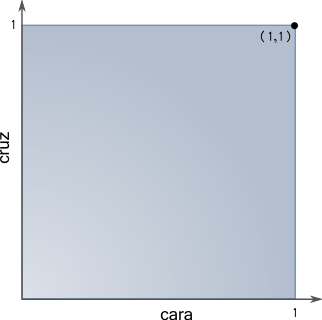
¡Es imposible que ese punto se corresponda con un estado de nuestra moneda! Significaría que ese estado es un 100% $\left | cara \right \rangle$ y un 100% $\left | cruz \right \rangle$ a la vez, ¡absurdo! Como recordarás, en el artículo anterior definimos $\left \langle estado1 | estado2 \right \rangle$ como el “grado de compatibilidad” de un estado con otro, y dijimos que su valor máximo era 1, cuando ambos estados eran el mismo. Aunque no voy a entrar en cálculo vectorial aquí, esa condición, en nuestro cuadrado, se traduce al hecho de que la distancia de cualquier estado al origen debe ser exactamente 1. Esto garantiza, entre otras cosas, que la probabilidad de observar “cara” o “cruz” al mirar la moneda sea siempre del 100% en total.
Puedes mirarlo de este modo: cualquier estado que no esté a una distancia 1 del origen no puede ser un estado real, porque al sumar las probabilidades de obtener “cara” y de obtener “cruz” al medir el valor del lado de la moneda, obtendríamos un valor de menos del 100% (en cuyo caso la moneda puede estar en algún estado que no es $\left | cara \right \rangle$ ni $\left | cruz \right \rangle$ al observarla y, entonces, hay algún autoestado que no habíamos considerado) o mayor del 100% (y entonces a veces es posible que la moneda esté al mismo tiempo en $\left | cara \right \rangle$ y $\left | cruz \right \rangle$, lo cual significa que esos estados no son autoestados). En cualquiera de los dos casos habríamos metido la pata: o faltan autoestados en un caso, o no son autoestados en el otro.
¿Ves ahora qué puntos de nuestro cuadrado sí se corresponden con estados posibles de la moneda? Si sabes geometría, probablemente ya lo ves: los puntos del interior del cuadrado que están a una distancia de 1 del origen, es decir, un cuarto de circunferencia. Pero hay una forma muy fácil de verlo, incluso si no estás muy puesto en geometría. Puesto que cualquier estado real de la moneda está a una distancia de 1 del origen (es decir, de la esquina inferior izquierda de nuestro cuadrado), imagina que tenemos una barra de longitud 1, y que ponemos un extremo justo en la esquina inferior izquierda: el otro extremo se encuentra siempre a una distancia 1 de ese punto, con lo que cualquier estado real de la moneda está sobre el otro extremo de la barra – si ahora movemos la barra (siempre con un extremo sobre el origen), el extremo opuesto “pinta” todos los posibles estados de la moneda, es decir, todos los puntos del cuadrado que distan 1 del origen:

Pensemos un momento en las consecuencias de lo que acabamos de hacer, que es bastante más profundo de lo que puede parecer en un principio:
En primer lugar, fíjate en ese trozo de circunferencia que acabamos de dibujar, y que representa gráficamente todos los estados posibles de la moneda. Como dijimos en la entrada anterior, hay infinitos estados, puesto que esa línea contiene infinitos puntos. Dos de ellos son especiales: los que se encuentran justo sobre los ejes, es decir, $(1,0)$ y $(0,1)$, que se corresponden con $\left | cara \right \rangle$ y $\left | cruz \right \rangle$. Permite que los escriba de una manera un tanto estúpida pero que –espero– pronto sea reveladora: $\left | cara \right \rangle = 1 \left | cara \right \rangle + 0 \left | cruz \right \rangle$, y $\left | cruz \right \rangle = 0 \left | cara \right \rangle + 1 \left | cruz \right \rangle$.
Cualquier otro estado posible de la moneda puede expresarse como un punto $(x,y)$ de ese cuadrado. Pero fíjate en lo que esto significa: las coordenadas $x$ e $y$ del punto nos indican cuánto de $\left | cara \right \rangle$ y cuánto de $\left | cruz \right \rangle$ tiene. Es decir, el punto $(x,y)$ representa un estado que podemos escribir como $\left | estado \right \rangle = x \left | cara \right \rangle + y \left | cruz \right \rangle$:

En nuestras coordenadas del cuadrado, ¿cómo escribiríamos el estado $\left | agitada \right \rangle$ del que hablamos hace dos artículos? Si lo recuerdas, se trataba del estado de la moneda cuando Dirac había agitado la caja una vez y nadie había mirado aún dentro de ella. Es posible que tu primer impulso sea decir que $\left | agitada \right \rangle = \frac{1}{2} \left | cara \right \rangle + \frac{1}{2} \left | cruz \right \rangle$, pero fíjate en nuestro cuadrado: el punto que representa ese estado, es decir, el punto $(\frac{1}{2},\frac{1}{2})$ no está a una distancia 1 del origen, está en el interior de la circunferencia, no sobre su borde.
No voy a entrar aquí en fórmulas matemáticas, pero gráficamente creo que es fácil ver que el punto que tiene “lo mismo de cara que de cruz” es el punto que se encuentra justo en el medio de nuestro arco de circunferencia, y sus coordenadas se pueden calcular utilizando el Teorema de Pitágoras (sumando el cuadrado de los dos catetos, es decir, las dos coordenadas $x$ e $y$, debe obtenerse la hipotenusa, es decir, 1). Sólo hay un punto que tenga lo mismo de cara que de cruz y diste 1 del origen:

Las coordenadas de ese punto, por si te interesan, son $(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$, y el estado $\left | agitada \right \rangle$ sí puede escribirse como $\left | agitada \right \rangle = \frac{1}{\sqrt{2}} \left | cara \right \rangle + \frac{1}{\sqrt{2}} \left | cruz \right \rangle$. Por supuesto, cualquier otro estado también puede escribirse como una combinación “ponderada” de los autoestados.
En segundo lugar, piensa en lo que acabamos de hacer: hemos representado todos los estados posibles de la moneda en un “sistema de coordenadas” que acabamos de inventar, en el que hemos empleado los dos estados propios como dimensiones. Hemos creado, por lo tanto, un espacio conceptual de dos dimensiones, dentro del cual se encuentran localizados (conceptualmente, claro) absolutamente todos los posibles estados de la moneda. No sé a ti, pero a mí esto me parece algo apabullante: los infinitos estados, constreñidos a una línea imaginaria (el arco de circunferencia) en un espacio conceptual cuyas dimensiones son los propios eigenestados del sistema.
No es necesario, por lo tanto, realizar complejos cálculos para determinar todos los posibles estados de la moneda: sólo hace falta calcular dos estados. Para cualquier otro estado sólo tenemos que calcular dos números: sus coordenadas en nuestro espacio bidimensional cara-cruz. Sí, a veces puede ser peliagudo calcular esos dos números, pero no me negarás que es una tarea menos imponente que enfrentarse a los infinitos estados posibles “a pelo”.
Pero es que hay mucho más: ten en cuenta que, hasta ahora, hemos trabajado con nuestra moneda, el sistema más simple que he podido imaginar. Creo que estamos listos para ir más allá. Imagina que tenemos un sistema algo más complejo que la moneda, aunque no mucho más: un dado de seis caras. En este caso voy a describir el sistema, los autoestados y todo lo demás bastante más rápido que en el caso de la moneda, porque parto de la base de que tienes el sistema de la moneda superado.
Simplificando todo lo necesario, nuestro sistema –el dado– tiene un observable, el lado que muestra al mirarlo. Al lanzar el dado, éste puede mostrar seis posibles valores del observable lado, es decir, puede mostrar 1, 2, 3, 4, 5 o 6. Estos seis valores se corresponden, por supuesto, con los seis autoestados del sistema, que son los seis estados en los que puede encontrarse el dado una vez que lo hemos lanzado. Llamemos a estos seis autoestados como sus valores asociados, para que sea evidente cuál es cuál: $\left | 1 \right \rangle$, $\left | 2 \right \rangle$, $\left | 3 \right \rangle$, $\left | 4 \right \rangle$, $\left | 5 \right \rangle$ y $\left | 6 \right \rangle$.
¿Cómo representar todos los demás estados del dado que no son autoestados? Pues, una vez más, utilizando los autoestados como las dimensiones de nuestro espacio conceptual. En este caso, y se trata de un simple y vulgar dado, ya aparecen cosas bien abstractas: no se trata ahora de un espacio de dos dimensiones, como en el caso de la moneda, ni de tres dimensiones como el que vemos con los ojos cuando miramos al mundo… se trata de un espacio de seis dimensiones, las correspondientes a los seis estados propios del dado.
Como comprenderás, en este caso no puedo utilizar dibujos para ayudarte a verlo, porque Geli todavía no ha aprendido a dibujar en 6D, pero sí podemos intentar imaginar –hasta donde es posible– a qué equivale la cosa. En el caso de la moneda teníamos dos dimensiones y dos coordenadas, ahora tenemos seis. En este espacio imaginario, cualquier estado del dado podría escribirse como un punto $(x,y,z,p,q,r)$, donde esas letras son las coordenadas del punto en el espacio. Todos los estados posibles del dado son puntos de ese tipo pero, una vez más, no todos los puntos posibles son estados del dado. No hace falta dibujar nada para ver esto: por ejemplo, creo que estarás de acuerdo conmigo en que el punto $(1,1,1,1,1,1)$ no es un estado posible, está “fuera de la circunferencia”.
Pero, claro, ahora no hay una circunferencia: estamos hablando de seis dimensiones. Imagina –para que sea más fácil de ver– que hubiéramos aumentado las dimensiones, pero no hasta seis, sino hasta algo más asequible: tres dimensiones, algo que sí podemos visualizar. En ese caso, la condición que pusimos (los puntos posibles son aquéllos que están a una distancia 1 del origen) se traduciría, no en los puntos del cuadrado que disten 1 del origen, es decir, un cuarto de circunferencia, sino en los puntos de un cubo de tres dimensiones que disten 1 del origen, es decir… una esfera. Si tienes visión espacial, espero que no tengas problema para ver eso – el conjunto de puntos del espacio que distan 1 de un punto determinado constituye una esfera en tres dimensiones.
En seis dimensiones, por supuesto, no aparece una esfera, pero la condición sigue siendo la misma: es el conjunto de puntos que están a una distancia 1 del origen. La generalización del concepto de “esfera” a un espacio de n dimensiones recibe el nombre de hiperesfera o n-esfera, y es lo que se obtiene en este caso. Sé que suena un poco a ciencia-ficción, pero los infinitos estados posibles del dado constituyen una hiperesfera en el espacio de seis dimensiones formado por los autoestados.

Sistema de descripción hiperesférica hexadimensional, vulg. “dado”. Crédito: Wikipedia/FDL .
Por ejemplo, el estado del dado justo antes de lanzarlo (suponiendo que no hacemos trampa y que nada favorece que salga un lado más probablemente que otro) es un estado que tiene lo mismo de todos los autoestados. No, no es $\frac{1}{6}$ de cada uno, porque entonces la distancia no sería 1: recuerda el caso de la circunferencia y cómo las coordenadas del “punto medio” no eran $(\frac{1}{2},\frac{1}{2})$, sino $(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$. En este caso sucede lo mismo, y podemos escribir el “punto medio” entre todos los estados como $(\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}})$.
En notación bra-ket, si llamamos al estado del dado antes de lanzarlo $\left | previo \right \rangle$, podemos decir que $\left | previo \right \rangle = \frac{1}{\sqrt{6}} \left | 1 \right \rangle + \frac{1}{\sqrt{6}} \left | 2 \right \rangle + \frac{1}{\sqrt{6}} \left | 3 \right \rangle + \frac{1}{\sqrt{6}} \left | 4 \right \rangle + \frac{1}{\sqrt{6}} \left | 5 \right \rangle + \frac{1}{\sqrt{6}} \left | 6 \right \rangle$. Quitémonos un sombrero n-dimensional ante Paul Dirac y compañía, señores.
Ah, pero la cosa no acaba aquí: si crees que los cuánticos se conforman con trabajar con espacios de seis dimensiones es que los subestimas. Apliquemos nuestra nueva “representación espacial” a un caso aún más complejo, y del que hemos hablado ya en la serie anteriormente: el pozo de potencial infinito. Si te hace falta, no dudes en releer la entrada antes de seguir con este artículo.
Como recordarás, una partícula dentro del pozo infinito no podía tener cualquier energía: sólo podía tener unos valores determinados. El valor más pequeño era el correspondiente al estado fundamental, y según aumentaba el número de nodos de la onda lo hacía también la energía que medíamos al mirar al electrón. ¿Qué quiere decir todo esto en los términos que venimos manejando ahora? En primer lugar, el observable que estamos midiendo en este caso es la energía del electrón, y cuando lo hacemos obtenemos una serie de posibles valores – no todos son posibles, sino sólo los correspondientes a los “escalones” que describimos en aquella entrada.
Es decir, las energías de cada escalón (la del estado con dos nodos, la del de tres, la del de cuatro, etc.) son los autovalores de la energía del sistema. Y los estados del electrón que describimos entonces son los autoestados del sistema. En aquel entonces nos limitamos a cavilar sobre lo que sucedía cuando mirábamos al electrón, pero ahora estamos listos para describir el estado del electrón en cualquier momento, no sólo al medir su energía.
Pero ahora la cosa es todavía más abstracta que en en el caso del dado. Como espero que recuerdes de aquel artículo sobre el pozo infinito, existen infinitos escalones de energía. Es decir, al construir ahora nuestro “espacio conceptual” utilizando los autovalores del electrón como las dimensiones del espacio… hay infinitas dimensiones, una por cada autoestado posible del electrón.
Llamemos, por ejemplo, $\left | E0 \right \rangle$ al estado fundamental del electrón (la onda de dos nodos en los extremos), $\left | E1 \right \rangle$ al siguiente “escalón”, $\left | E2 \right \rangle$ al siguiente, etc. Entonces, cualquier estado posible del electrón –antes o después de mirarlo– puede expresarse como un punto en un espacio de infinitas dimensiones, cuyas coordenadas serán $(a,b,c,d,…)$. Sí, dentro del paréntesis hay infinitas coordenadas. Raro, ¿eh?
En nuestra notación de Dirac, cualquier estado del electrón puede escribirse como $\left | E \right \rangle = a \left | E0 \right \rangle + b \left | E1 \right \rangle + c \left | E2 \right \rangle + d \left | E3 \right \rangle …$ y así hasta el infinito. Naturalmente, algunos de los estados posibles del electrón no son sumas infinitas, porque tal vez no incluyen a todos los autoestados, sino que muchas de sus coordenadas son cero. Por ejemplo, supongamos que el electrón se encuentra “a medias” entre los estados $\left | E0 \right \rangle$, $\left | E1 \right \rangle$ y $\left | E2 \right \rangle$. Entonces, su estado será (recuerda que la distancia debe ser siempre 1, y las raíces correspondientes) $\frac{1}{\sqrt{3}} \left | E0 \right \rangle + \frac{1}{\sqrt{3}} \left | E1 \right \rangle + \frac{1}{\sqrt{3}} \left | E2 \right \rangle$.
Pero, por supuesto, otros estados sí pueden involucrar infinitas coordenadas no nulas. Es decir, en general, un estado cuántico se corresponde con un punto cualquiera de una hiperesfera en un espacio de infinitas dimensiones. Podrías pensar que, llegados a este punto, sólo hay dos opciones: asumir la propia demencia y hundirse en un mundo de ilusión y fantasía delirantes, o abandonar cualquier esperanza de estudiar estas cosas. Sin embargo, curiosamente, para cuando la cuántica alcanzó este grado de madurez, las matemáticas ya habían llegado hasta aquí.
Sí, puede resultar extraño, pero alguien había definido ya el concepto de un espacio parecido al euclídeo que podemos ver, pero con infinitas dimensiones, y había desarrollado las matemáticas necesarias para operar con esos espacios. Ese genio –porque no merece otro calificativo– no es otro que David Hilbert, que ya ha aparecido en El Tamiz hace un tiempo (también hablando en aquella ocasión del concepto de infinito). Y estos espacios conceptuales reciben el nombre, en su honor, de espacios de Hilbert.
Puede parecer que no es posible algo más abstracto y difícil de imaginar que el caso del pozo infinito y similares, pero lo hay; no vamos a hablar de ello hoy, porque tiene sutilezas que deberíamos preparar mejor, pero si conoces la diferencia entre un número infinito pero contable y otro incontable (como, por ejemplo, la diferencia entre los números naturales y los números reales) puedes comprender el horror en el que puede convertirse todo esto: en el caso del pozo infinito existen tantos estados como números naturales hay… pero también es posible tener un número infinito e incontable de dimensiones en un espacio de Hilbert. Por ejemplo, recordarás que la energía de un sistema cuántico “encerrado”, como el electrón en el pozo infinito, sólo puede tomar valores escalonados… pero esto no sucede para un sistema libre: un electrón –por decir una partícula concreta– que viaja libre por el espacio puede tener cualquier energía. Entonces, los infinitos autoestados del sistema no son valores discretos, sino cualquier valor real de la energía. Tenemos entonces un espacio ∞-dimensional con tantas coordenadas como existen números reales. Si no puedes imaginarlo, bienvenido al club: ¡cállate y calcula! (al menos a ti, a diferencia de mí, alguien ha intentado explicártelo en términos que pueden comprenderse hasta cierto punto).
Además, lo que acabamos de describir son estados cuánticos puros; también existen, cuando el sistema consta de muchas partículas, por ejemplo, estados cuánticos mixtos en los que la estadística tiene aún más que decir, pero por ahora no nos preocuparemos de ello – simplemente recuerda que, aunque esto sea complicado, aún hay más complicaciones en la formulación cuántica moderna. Pero, por otro lado, si has entendido esto no dejes que el hecho de que existan otras complicaciones te quite la satisfacción de haber comprendido algo realmente complejo. ¡Saborea el momento!
Dentro de unas semanas continuaremos nuestro viaje por las procelosas aguas de la física cuántica aplicando estos conceptos a otros sistemas que ya hemos estudiado antes, pero primero volveremos a otras series más pedestres que tenemos abandonadas, como la del Sistema Solar. Entre otras cosas, la OMS recomienda no leer más de tres entradas seguidas sobre cuántica, ”[…] o la mente del lector puede ser empujada más allá de los débiles límites de la cordura de modo que las simples tres dimensiones del espacio euclídeo se difuminen, revelando un Universo en el que los mitos de Cthulhu parecen cuentos de abuela”. Hasta la próxima, en la que hablaremos del gato de Schrödinger.
El crédito de todas las imágenes es de Geli J. Crick, Licencia Creative Commons 2.5-España de Atribución, Sin obras derivadas y No comercial (como atribución basta incluir este mismo mensaje y un enlace a este artículo).
Para saber más:
