El Cedazo

En anteriores capítulos de esta serie hemos visto cómo se representaban en binario los números naturales y luego cómo hacer circuitos que permitan hacer operaciones con ellos. Hoy vamos a ampliar la explicación hasta llegar a los números negativos.

La forma más habitual de representar números negativos en binario es el complemento a dos, pero veremos entre medias algunas otras formas.

 

 

Bit de signo o signo-magnitud

La forma más sencilla que se nos ocurre es utilizar un bit adicional para representar el signo de un número. Como recordarás, decíamos que tamaños de 8 bits, 16 bits o 32 bits eran muy habituales, pero nosotros hemos utilizado en todos nuestros ejemplos únicamente 7 bits. Así que supongo que no te sorprende si ahora decidimos utilizar el bit inicial, ese que nos sobra, para representar el signo.

Así, con nuestra notación anterior de 7 bits, teníamos por ejemplo los siguiente números:

5: 0000101

7: 0000111

13: 0001101

Podemos decidir que nuestra representación de enteros con signo será tal que el primer bit será 0 si es positivo y 1 si es negativo, dejando los últimos 7 bits para el número en sí. Así, por ejemplo, podemos representar los siguientes números de la siguiente forma:

+5: 00000101

+7: 00000111

+13: 00001101

-5: 10000101

-7: 10000111

-13: 10001101

El principal inconveniente de esta aproximación es que hacer sumas y restas es complicado. No es que sea imposible, pero necesitamos un circuito para hacer sumas como el que vimos en el capítulo anterior, y otro circuito diferente para hacer restas. Otra forma de verlo es que esos circuitos tienen subcircuitos dependiendo del signo de los operandos. Se puede hacer, pero no es eficiente.

Representar los enteros así tiene un inconveniente más, que es que el 0 se representa dos veces: +0 se pondría 00000000, mientras que -0 se pondría 10000000. Pero +0 y -0 son el mismo número, y no nos gusta tener dos representaciones para el mismo número (eso nos complicaría la vida más adelante).

La ventaja más importante de esta representación de “signo-magnitud” la veremos más adelante, cuando veamos los inconvenientes de las siguiente representaciones. Tiene una cosa buena, pero es igual en todas las formas que veremos, de modo que técnicamente no es una ventaja: podemos saber si un número es positivo o negativo simplemente mirando el primer bit.

Complemento a uno

En esta representación los números positivos se representan simplemente como hemos visto los naturales, pero poniéndoles un 0 delante. O sea, ningún cambio respecto a la anterior. La diferencia es en los números negativos: se representan dándole la vuelta a todos los bits; los 1 pasan a 0 y los 0 a 1. Así, los números negativos de antes se representarían de la siguiente forma:

-5: 11111010

-7: 11111000

-13: 11110010

Este sistema tiene una ventaja, que es que ahora las sumas y restas sí son sencillas. Sabemos desde el colegio que restar 13-7 es lo mismo que sumar 13+(-7) o (-7)+13… bien, pues todo esto es cierto en la representación en complemento a uno, simplemente sumándolos con el mismo algoritmo que veíamos para los naturales (con un pequeño truquillo, que ahora veremos).

Sí por ejemplo queremos restar 13-7, simplemente podemos sumar 13 y -7:

Uhm… un momento… ¿qué es eso de “y me llevo 1″? Esta operación no da overflow, ¿por qué me sobra 1? Y peor aún: yo sé que 13-7 son 6, pero 00000101 no es 6, sino 5. Bien, este es el truquillo que decía: si sale un acarreo no es que haya habido overflow, sino que hay que volver a metérselo y sumarlo. Es decir, el 1 que le llevo lo vuelvo a meter por un sumador:

Ahora sí, encaja.

Tiene este sistema dos desventajas. Una es la misma que tendrá el complemento-a-dos que veremos luego, así que no la contamos todavía. La otra es que sigue representando el +0 y el -0 con dos formas distintas (00000000 y 11111111 respectivamente), y eso definitivamente sigue sin gustarnos.

Complemento a dos

Finalmente llegamos a la forma más utilizada: el complemento a dos. La forma de calcular la representación binaria de un número negativo en complemento-a-dos es calcular la del complemento-a-1 y sumarle 1 (los números positivos se representan igual). Veamos un ejemplo.

+7 se representa 0000111.

-7 en complemento-a-1 se representaría 1111000.

-7 en complemento-a-2 se representaría sumando 1111000 más 1. Es decir: 1111001.

Existe una forma rápida de hacer mentalmente la conversión. Representamos el 7 en binario: 0000111. Empezamos por el bit de más a la derecha y si es un 0, lo dejamos como está, y miramos el siguiente bit. Si es un 1, también lo dejamos como está… pero a partir de ahora, en los siguientes bits, ya no miramos si son 0 ó 1: los intercambiamos siempre. Veamos cómo sería para por ejemplo el -12.

12: 00001100

-12: xxxxxxx0 (como es un 0, lo copiamos sin cambiarlo)

-12: xxxxxx00 (lo mismo)

-12: xxxxx100 (el 1 también lo copiamos sin cambiarlo… pero a partir de aquí…)

-12: xxxx0100 (… de aquí en adelante siempre cambiamos 0 por 1 y viceversa)

-12: xxx10100

-12: 11110100

Prueba ambos métodos y verás que son equivalentes. Los mismos ejemplos de antes:

-5: 11111011

-7: 11111001

-13: 11110011

Una de las ventajas de esta forma de representación es que el 0 ya no se representa de dos formas distintas. Solo puede representarse como 00000000.

De esta forma, si tenemos 8 bits, podemos representar desde el -128 hasta el 127. De forma genérica, si tenemos n bits, podemos representar desde el hasta el .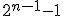

La otra ventaja que tiene es que restar un número es sumar el complemento a dos, y esta vez sin truquillos de ningún tipo. Si queremos hacer 7-5, podemos hacer sin problemas 7+(-5):

La principal desventaja del complemento-a-dos es que hacer multiplicaciones es un poco más difícil (y esta era la ventaja que no queríamos adelantar de la forma signo-magnitud). Ojo, que no es imposible, simplemente requiere más puertas que la multiplicación con la representación de signo-magnitud. Así que los estudiosos de esto se pusieron a analizarlo y parece que la ventaja de poder hacer la suma/resta con facilidad es más importante que poder hacer la multiplicación con facilidad (un computador hace normalmente muchísimas más sumas que multiplicaciones) y por eso casi todos los sistemas modernos usan el complemento a dos para representar los números negativos.

No obstante, no te apresures a olvidar la representación signo-magnitud, porque aún la usaremos más adelante.

Exceso a X

Existe una forma adicional de representar números negativos… que es representarlos todos en positivo.

A ver si me explico.

Es obvio que podemos ordenar los números binarios de 8 bits, empezando por el más pequeño, el 0000 0000. Luego iría el 0000 0001. Luego el 0000 0010. Y así sucesivamente, hasta llegar al 1111 1111. Fácil.

Pero, ¿por qué hemos dicho que el 0000 0000 es el 0? Podríamos simplemente decir que el 0000 0000 significa -127. Por lo tanto, el 0000 0001 significa -126. El 0000 0010 significa -125. Y así sucesivamente hasta el 0111 1111, que significa 0. 1000 0000 significaría entonces 1. Y seguimos hasta el 1111 1111, que significa 128. Vamos a ponerlo en forma de tabla, que es un poco lioso.

Esta notación se llama “exceso-127″ porque está desplazado 127 números hacia arriba. Para pasar de decimal a binario-exceso-127 no hay más que sumar 127 al número a convertir antes de pasarlo a binario. Y al revés, para pasarlo de binario-exceso-127 a decimal, simplemente hay que restarle 127 una vez que lo hayamos transformado.

Obviamente, existen otros “excesos”. Se nos podría ocurrir por ejemplo “exceso-42″. Sería posible… pero su utilidad sería marginal. Cuando se elige el 127 es porque con 8 bits podríamos representar desde el 0 al 255 (si solo queremos positivos, es decir exceso-0) o desde el -127 hasta el 128, si queremos un rango simétrico hacia arriba y hacia abajo (exceso-127).

En el próximo artículo veremos cómo representar los números reales (o al menos una aproximación razonable).