Seguimos con esta serie en la que con anterioridad, y antes de hablar del modelo atómico de Thomson, he hablando sobre varios conceptos de física general que está bien saber y serán importantes para entender el modelo en cuestión. En los dos últimos artículos hablamos sobre la conservación de la energía y el momento lineal y sobre colisiones elásticas. Bien, hoy salimos del ámbito general de la mecánica (aunque de lo que hablaremos sigue siendo básicamente mecánica) para adentrarnos con la física de las oscilaciones. Empecemos:
3. Movimiento armónico
Antes de nada, empecemos por el principio. Seguro que todos conocéis los movimientos rectilíneos y circulares, pero ¿qué es un movimiento oscilatorio? ¿Qué diferencia hay entre un movimiento oscilatorio, un movimiento periódico y un movimiento armónico?
Bien, un movimiento periódico seguro que sabéis qué es, ya que es bastante intuitivo. Un movimiento periódico es un movimiento que se repite a intervalos regulares de tiempo. La Tierra gira alrededor del Sol en un movimiento periódico, un péndulo simple también se mueve con un movimiento periódico, pero los trenes también se mueven con un movimiento periódico al hacer el mismo recorrido una y otra vez.
Dentro del conjunto de los movimientos periódicos está el movimiento oscilatorio.[1] Un objeto que se mueve con un movimiento oscilatorio se mueve de un lado hacia otro periódicamente pasando siempre por un punto de equilibrio[2]. De los ejemplos mencionados arriba sólo es un movimiento oscilatorio el del péndulo simple; el resto son periódicos, pero no oscilatorios.
Dentro de los movimientos oscilatorios hay un caso particular, el movimiento vibratorio, que es un movimiento oscilatorio en el que el objeto se mueve con una trayectoria rectilínea. El péndulo simple sigue un movimiento oscilatorio no vibratorio (aunque si el ángulo es muy pequeño se puede aproximar bastante bien a un vibratorio).
Y finalmente, un tipo de movimiento vibratorio es el movimiento armónico, que es un movimiento vibratorio producido por una fuerza conservadora o, lo que es lo mismo, recuperadora.
El caso de un muelle es el ejemplo típico de un movimiento armónico. Y nos ayudará a entender el concepto de fuerza conservadora[3] o recuperadora. Bien, imaginemos un muelle; todos sabemos que si intentamos estirarlo, el muelle hace una fuerza que tiende a comprimirlo hasta sus dimensiones iniciales. Del mismo modo, si lo comprimimos el muelle hace una fuerza que tiende a estirarlo hasta sus dimensiones iniciales de nuevo. Es decir, el muelle tiende a recuperar su estado inicial. Pues bien, una fuerza recuperadora no es nada más que esto.
Bien, supongamos que el muelle tiene un extremo fijado. El otro extremo estará a cierta distancia que nombramos posición de equilibrio. En esta posición el muelle no sufre ninguna fuerza. Si estiramos el muelle (diremos que tiene una elongación positiva) aparece una fuerza que lo comprime; por el contrario si lo comprimimos (diremos que tiene una elongación negativa) aparece una fuerza que lo alarga. Es decir, que la fuerza restauradora siempre va en sentido contrario que la elongación. Pero además todos hemos jugado alguna vez con un muelle y sabemos que cuanto más lo estiramos/comprimimos más grande es la fuerza que ejerce. Por lo que, además de saber que tiene signo contrario a la elongación, sabemos que es proporcional a ella. Voy a profundizar algo más en esto en el apartado con ecuaciones ya que es bastante importante para entender el movimiento.
Imaginemos ahora que colgamos una masa en el muelle y lo alargamos un poco, aparecerá una fuerza conservadora que hará que el peso suba hacia arriba. Pero hemos dicho que la fuerza conservadora es conservativa, por lo que, cuando alargamos el muelle estamos aportando energía potencial al sistema. Cuando el peso sube hacia arriba la energía potencial (que llamaremos energía potencial elástica) disminuye y aumenta la energía cinética, hasta que en la posición de equilibrio la energía potencial elástica es 0 (la fuerza conservadora es nula). Pero el objeto tiene energía cinética, por lo que no se para sino que sigue subiendo y la energía cinética se convierte ahora otra vez en energía potencial elástica.[4] El peso sube y baja a intervalos constantes de tiempo, pasando por una cierta posición de equilibrio, siguiendo un movimiento rectilíneo, y todo esto debido a una fuerza restauradora… ¡Tenemos un movimiento armónico!
Por lo tanto podemos definir el período del movimiento: el período es, por ejemplo, el tiempo que tarda en subir y bajar, o el tiempo que tarda en pasar dos veces (en el mismo sentido) por la posición de equilibrio… También podemos definir la frecuencia como el número de oscilaciones que hace en una unidad de tiempo, por ejemplo cada segundo. Parece evidente que el período dependerá de dos factores: lo “rígido” que sea el muelle (un muelle es más rígido que otro si para una misma elongación la fuerza que ejerce es mayor) y la masa que colguemos del muelle. De hecho cuanto más pese la masa que colguemos del muelle más tardará en completar una oscilación, del mismo modo que cuando más rígido sea el muelle más rápido completará una oscilación.
Como la frecuencia es la inversa del período,[5] la frecuencia aumentará con la rigidez del muelle y disminuirá con la masa que colguemos.
Bien, es importante que en este artículo hayan quedado claros estos conceptos:
- Qué es un movimiento armónico.
- La fuerza recuperadora es proporcional a la elongación y de sentido opuesto (en un muelle la constante de proporcionalidad nos indica la rigidez).
- La frecuencia de un muelle aumenta con la rigidez y disminuye con la masa que colguemos de él.
Movimiento armónico (con ecuaciones)
Hemos visto en la primera parte del artículo lo que era un movimiento armónico, además hemos visto que, primero, la fuerza recuperadora es proporcional a la elongación y, segundo, que tiene signo contrario a esta.
Donde en un muelle k nos indica su rigidez.
Vemos claramente que si x es positivo la fuerza será negativa (si estiramos el muelle, la fuerza lo comprime) y que si x es negativo la fuerza será positiva (si comprimimos el muelle, la fuerza lo estira).
Ahora bien, alguien podría preguntarse ¿por qué x? ya que las siguientes ecuaciones también se adaptan a este fenómeno:
Vemos que sólo sirven las potencias impares, ya que si fueran pares la fuerza seria siempre negativa (tendería a comprimir el muelle, aunque tú lo comprimieses también).
Es una buena pregunta. Pues bien, la verdad es que, en realidad, la fuerza es de la forma siguiente:
Pero para simplificar el tratamiento matemático se suele tomar sólo el término lineal, lo que experimentalmente se comprueba que es una muy buena aproximación, sobre todo para elongaciones pequeñas. Al movimiento que se obtiene considerando sólo el término lineal de la fuerza recuperadora, y además suponiendo que todas las fuerzas que actúan son conservativas, se le nombra como Movimiento Armónico Simple y es en realidad del que vamos a hablar aquí.
Si colgamos una masa m y suponemos que la única fuerza que actúa es la fuerza recuperadora (lo que no resta generalidad, aunque no demuestre aquí el porqué) la segunda ley de Newton nos dice que:
Donde d2x/dt2 es la segunda derivada de la elongación respecto del tiempo y ω es una constante que depende del muelle y la masa.
Lo que tenemos es una ecuación diferencial, no la voy a resolver aquí porque es largo y matemáticamente complejo. Así que mágicamente vamos a suponer que la solución tiene la siguiente forma:
AVISO: Ahora voy a hacer unos cálculos matemáticos para los que necesitas no sólo conocer el concepto de derivada sino también saber derivar funciones simples. Esto no es para nada necesario para entender el MAS (siglas de Movimiento Armónico Simple) y mucho menos para seguir la serie. Pero creo que es suficientemente fácil e importante como para incluirlo aquí, aunque puedes saltártelo sin ningún problema.
Comprobemos que efectivamente es solución de nuestra ecuación:
Efectivamente nuestra suposición es perfectamente válida.
Pero… ¿qué nos dice esta solución?
Primero de todo, nos dice cuánto vale x (la elongación) en cada instante de tiempo, por lo que si conocemos todas las variables podemos saber dónde estará la masa en todo momento.
A representa la amplitud del movimiento, es decir, la elongación máxima (efectivamente, el coseno se mueve entre 1 y -1).
ω es la constante que depende de la masa y el muelle como hemos definido antes.
φ es una constante que depende de la elongación en t=0, el momento inicial.
ωt-φ es lo que se llama la fase del movimiento (φ se puede llamar constante de desfasamiento).
Además, como el coseno es una función periódica, el movimiento también lo es. Como hemos dicho, el período se definía como el tiempo que tarda la masa en hacer una oscilación, y sabiendo que la función coseno tiene un período de 2π podemos establecer la siguiente relación:
Donde T es el período del movimiento (efectivamente, cuando hayan pasado T segundos la fase habrá aumentado 2π). A partir de aquí es muy fácil saber el período:
Y por definición la frecuencia es:
Donde vemos que claramente cumple lo que intuitivamente habíamos predicho.
Además se puede notar una consecuencia muy importante: tanto el período como la frecuencia son independientes de la amplitud del movimiento, por lo que el muelle tardará lo mismo en hacer una oscilación de 2cm que otra de 2m.
Como curiosidad, ¿alguna vez os habéis preguntado cómo se puede medir una masa en el espacio? En la Tierra es muy fácil, conociendo la aceleración que ejerce la Tierra sobre un cuerpo sólo es necesario medir la fuerza de atracción para obtener la masa (es lo que hace una balanza). Pero en el espacio una balanza marcaría 0 ya que en el espacio todos los cuerpos caen en una caída libre que hace que se experimente un efecto de ingravidez y por lo tanto que hace que una balanza no marque ningún peso.
Pues bien, sólo es necesario un resorte del cual conozcamos su constante elástica (que es la misma en la Tierra, en Júpiter o en Alfa Centauri) y medir cuánto vale la frecuencia de vibración.
Terminamos el artículo por hoy, espero que haya quedado bastante claro este movimiento, ya que es muy importante para la física en general. En el siguiente capítulo vamos a hablar de electrostática (hablar de un átomo compuesto por cargas positivas y negativas sin hablar antes de electrostática sería un poco tonto ¿no?). Por cierto, hemos llegado a la mitad de esta introducción y espero que la espera no se os esté haciendo demasiado larga. Dentro de poco deberíamos empezar ya con el modelo atómico de Thomson.
Hasta la próxima.
- Ojo, un movimiento oscilatorio no es lo mismo que periódico, pues un movimiento periódico puede no ser oscilatorio. [↩]
- Punto donde la fuerza total es nula. [↩]
- OJO: no confundir fuerza conservadora con la fuerza conservativa que vimos en el primer artículo, aunque el nombre de “conservadora” viene de que efectivamente es una fuerza conservativa, pero los conceptos son distintos. [↩]
- Ignoremos la energía potencial debida a la gravedad. [↩]
- Si el período es de x, la frecuencia será de 1/x. [↩]

The [De Thomson a Bohr, historia de un átomo] 0-Conceptos previos 3: Movimiento Armónico by Roger Balsach, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.




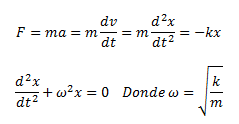
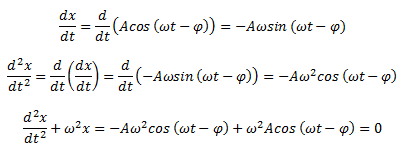



Escribe un comentario