En el post anterior estudiamos por qué nació la necesidad de crear un altavoz, su rápido desarrollo, su funcionamiento y finalmente el primero de sus problemas… Como dijimos, estos problemas no son debidos a un error de diseño (aunque un error de diseño empeora todo, por supuesto) sino que son limitaciones físicas del mundo en el que vivimos. La buena noticia es que como somos seres inteligentes (bue… eso dicen por ahí) no nos contentamos con aceptar estas limitaciones inherentes al diseño de los primeros altavoces y empezamos una larga carrera para poder desarrollarlos y mejorar su fidelidad. Después de cien años… ¡Los altavoces siguen siendo muy parecidos! Es más, su principio de funcionamiento sigue siendo el mismo, tan sólo hemos añadido algunos detalles, nada más, pero son precisamente esos detalles los que lograron que la fidelidad mejorara muchísimo.
Antes de continuar hay que hacer algunas aclaraciones sobre el sonido[1] para entender mejor el concepto. Como ya sabemos, un sonido es una onda que se desplaza por un medio material, comúnmente el aire. Dicho sonido tiene una frecuencia determinada, y a más alta esta frecuencia, más “agudo” escuchamos el sonido, y a menor frecuencia lo escuchamos más “grave”. Para facilitar las cosas, los rangos de frecuencias se dividieron en diferentes tipos.
Los sonidos “graves” son los que se encuentran entre los 20Hz, que es la mínima frecuencia que el oído humano puede sentir (aunque cada ser humano tiene límites ligeramente distintos, más o menos por debajo de esa frecuencia no oímos nada) y aproximadamente los 320Hz. O sea, que cuando escuchamos un bajo o un bombo, que suenan “graves”, estamos sintiendo una onda de baja frecuencia, normalmente entre las dos frecuencias citadas.
Los sonidos “medios” son los que su frecuencia se encuentra entre los 320Hz y los 2560Hz aproximadamente. Entre estos sonidos tenemos la mayor parte de las notas del piano, la voz humana, las guitarras y un sin fin de instrumentos más.
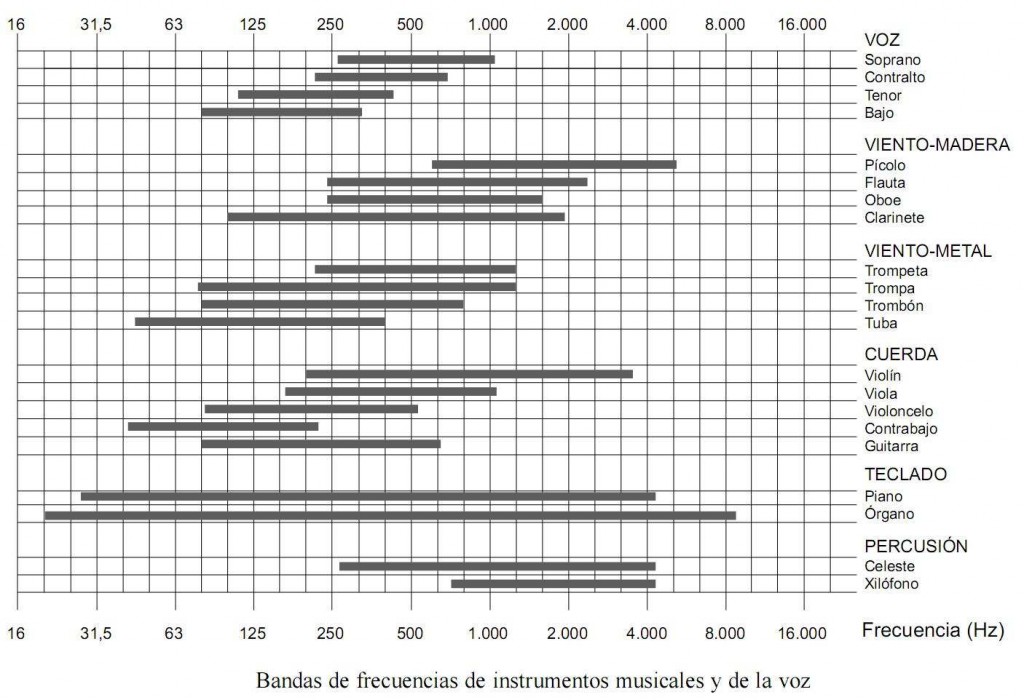
Y los sonidos “agudos” son los comprendidos entre los 2560Hz y los 20000Hz, que es el límite superior que la mayoría de los oídos humanos pueden oír cuando somos jóvenes (si… los viejos ya no oyen nada a partir de unos 16000Hz). Entre los agudos tenemos los platillos, las notas más agudas de los violines, las campanas, y mayormente los armónicos de las frecuencias menores que son los que le dan el “timbre” característico a cada instrumento y que estudiaremos más adelante. En la siguiente ilustración tenemos los rangos aproximados de algunos instrumentos:
Pero acá aparece algo extraño: los graves sólo tienen un rango de 300hz, los medios un rango de unos 2000hz y los agudos un rango de ¡18000hz! ¿Por qué tanta diferencia? ¿Por qué los agudos son “privilegiados” y contienen la mayor parte del espectro auditivo? Esto es por que el oído no siente los sonidos linealmente, sino de forma “logarítmica”. Para entenderlo mejor, una simple analogía bastará.
Pongamos una moneda en nuestra mano. Vamos a sentir su peso; ahora añadamos otra moneda, vamos a sentir el doble de peso, ahora añadimos otra más, ya no vamos a sentir el doble de peso, sino una fracción de él: para sentir el doble de peso hay que poner dos monedas más. Supongamos que seguimos con el experimento y ya tenemos 100 monedas en nuestra mano, si añadimos sólo una moneda más… casi no notaremos variación en el peso total, tendríamos que poner otras 100 para notar nuevamente el doble de peso, y ni hablar de cuando lleguemos a 1000 monedas (¡somos fuertes! ¡y ricos!) el peso de una sola moneda ya será despreciable y casi imposible sentir la diferencia de peso entre 1000 monedas y 1001. ¿Se entiende la idea? El tacto también trabaja de forma logarítmica.
Nuestro oído puede detectar sin problemas una variación de 60Hz a 61Hz, pero no de 10000Hz a 10001Hz ya que nuestro oído también trabaja de forma logarítmica. De esta forma, el sonido se dividió en octavas, que son las siguientes en Hz: 20 a 40, primera; 40 a 80, segunda; 80 a160, tercera; 160 a 320, cuarta; 320 a 640, quinta; 640 a 1280, sexta; 1280 a 2560, séptima; 2560 a 5120, octava; 5120 a 10240, novena; y de 10240 a 20480, décima. O sea, a cada altavoz le tocan sólo algunas octavas y nada más. Ahora sí, ninguno tiene privilegios. Pero no nos vayamos por las ramas, ya que con estos datos podemos continuar.
Como dijimos, el primer avance fue dividir las tareas, en términos acústicos: Diseñar un altavoz para cada rango de frecuencias, ya que los grandes pueden oscilar lentamente pero generar gran amplitud, los medianos pueden oscilar más rápidamente, pero con una amplitud menor y los pequeños pueden oscilar rapidísimo, pero su amplitud es muy baja. Podemos rápidamente determinar que a más amplitud, más energía en juego, y ahora sí, ¡la física nos juega a favor! En el espectro auditivo, los sonidos graves tienen normalmente el 65% de la energía acústica por su gran amplitud, y como los altavoces diseñados para sonidos graves son grandes y con gran amplitud, ¡pueden emitir perfectamente toda esa energía! Los sonidos medios tienen aproximadamente el 25% de la energía acústica total, por lo que un altavoz más pequeño la podrá manejar sin problemas, y al ser pequeño podrá reproducirlos mejor que uno grande. Y a los agudos sólo les toca el 10% de la energía total, ya que los mismos tienen una amplitud muy baja, pero oscilar a 20000Hz no es cosa fácil. Por eso es que los altavoces de agudos son pequeñísimos y livianos, pero como la energía que tienen que emitir es baja… no hay inconvenientes.
Esta división de tareas dividió básicamente los tipos de altavoces en cuatro, que vamos a detallar a continuación.
Altavoces de graves, que ahora los llamaremos por su nombre en ingles “woofer”. Son grandes altavoces para mover la mayor cantidad de aire posible, generalmente entre ocho y dieciocho pulgadas (en los altavoces el diámetro se mide en pulgadas y todas las otras medidas en mm… parece que nadie se puso de acuerdo en seguir un solo sistema de unidades). Cuanto más grandes son, más aire mueven, o sea, logran mayor presión sonora, pero menos rango de frecuencias reproducen, por lo general woofers de 18´´ y 15´´ solo reproducen “fielmente”[2] hasta unos 150Hz, los de 12´´ y l0´´ hasta unos 400Hz y los de 8´´ hasta los 1000Hz normalmente. Estos woofers siempre tienen que ir acompañados de los dos siguientes tipos de altavoces ya que, si no, no es posible reproducir fielmente todo el espectro auditivo.
Altavoces de medios, que los llamamos “mid-range”. Consisten en pequeños altavoces constructivamente iguales a sus hermanos mayores, los “woofers”, pero al tener un tamaño mucho menor, del orden de 5´´ a 2´´ su masa es muchísimo menor y no tienen problemas en llegar a frecuencias del orden de 3000Hz a 5000Hz. Estos altavoces, como veremos más adelante, son críticos, ya que por el mismo se reproducen la mayoría de los instrumentos y la voz humana.
Pero antes de pasar al siguiente tipo de altavoz necesitamos ver otro tema, que también es inherente al diseño de los altavoces que estamos estudiando, y por esta causa los diseños de altavoces de agudos son totalmente distintos.
Las ondas sonoras tienen una frecuencia determinada. Como la velocidad del sonido en el aire es de unos 336 m\s, podemos determinar la longitud de onda para cada frecuencia. Así, para 20Hz la longitud es de unos 16.8 metros, para 2000hz, unos 16,8 centímetros, y para 20000Hz, unos 1,68 milímetros. Presten atención a lo siguiente, porque es importantísimo: Cuando un altavoz emite una onda cuya longitud de onda es mayor que su diámetro, éste radia esféricamente en todas las direcciones, o sea, que no importa donde nos ubiquemos: vamos a escuchar igual los sonidos mientras estos tengan una longitud de onda mayor que el diámetro del altavoz que lo reproduce. Por ejemplo, un altavoz de 6.5´´ va a emitir sonido esfericamente hasta una frecuencia de 2000Hz aproximadamente (lo podemos deducir fácilmente con la formula “Velocidad del sonido / frecuencia = longitud de onda”), y uno de 18´´, hasta unos 735Hz.
¿Qué pasa cuando la longitud de onda empieza a ser menor que el diámetro del altavoz? Pues sucede un efecto llamado “difracción por borde” y el altavoz entra en una transición de emitir cada vez más direccionalmente hacia delante. Esto tiene dos problemas: uno es que si nos ponemos justo delante del altavoz escuchamos bien todo, pero si nos movemos a un lado, escuchamos sólo las frecuencias cuyas longitudes de onda son mayores que el diámetro, y las menores, no, y segundo, como antes la energía la distribuíamos esféricamente en todo el espacio circundante, a cada punto llegaba cierta cantidad que obedecía a la regla “disminuye con el cuadrado de la distancia”, pero ahora que el altavoz esta radiando sólo hacia adelante, ¡concentra toda la energía en una dirección!, haciendo que en ese punto los sonidos cuya longitud de onda es menor que el diámetro del altavoz suenen mucho más “fuerte” o sea, con mayor presión sonora. Como vemos, recién llevamos dos artículos introductorios y se complicó todo…
Volvamos al asunto. En altavoces de graves y medios esto por lo general no es un problema, ya que normalmente reproducen frecuencias cuya longitud de onda es mayor que su diámetro[3] y podemos usar para ellos un diseño clásico, pero cuando la frecuencia a reproducir es muy alta la longitud de onda se achica drásticamente, al orden de milímetros, y, como supondrán, no es viable hacer altavoces tan chicos, ya que por más que sólo se reproducirán por los mismos solo el 10% de la energía, hay un tamaño mínimo. Acá es donde entra en juego el intelecto humano para poder diseñar un altavoz de mayor tamaño que la frecuencia reproducida y que éste radie en forma “cuasi-esférica”.
Ahora sí:
Altavoces de agudos, a los que normalmente se les denomina “tweeter”. Acá todo es ya distinto, por lo que dijimos. En vez de usar el típico diseño exponencial, descubrimos que a altas frecuencias una forma de domo podía radiar más esfericamente (no al 100%, pero mucho mejor que el típico cono). El domo se llevó a valores de 1.5´´ a 0.5´´, y gracias al diseño de su domo, podían emitir sonidos a altas frecuencias bastante omnidireccionalmente, además de que se desarrollaron muchísimas tecnologías totalmente distintas, como tweeters de cinta, piezoeléctricos, anillo radiante, motores de compresión, etc. Pero como el 90% de los tweeters para alta fidelidad son de tipo “domo”, sólo estudiaremos este tipo y tal vez algo de “anillos radiantes”, ya que se están poniendo muy de moda y su principio de funcionamiento es el mismo que el de los transductores electroacústicos.
Vimos en un ejemplo anterior que un altavoz de 6.5´´ puede reproducir teóricamente hasta 2000Hz sin problemas. A los woofers de este tamaño aproximado entre 7´´ y 5.5´´ se les llama “mid-woofer” por que si están bien y específicamente diseñados para esto, pueden reproducir graves gracias a su tamaño, no con la presión sonora de uno más grande, pero sí lo suficiente para un uso hogareño, y reproducir medios gracias a su baja masa. Estos, unidos con algún tweeter de diseño eficiente que reproduzca desde unos 2000Hz nos dan también toda la banda auditiva, pero con dos altavoces en ves de tres. En la jerga se les llaman “dos vías y tres vías”.
También existen los denominados “sub-woofer”, que no son más que un woofer diseñado para reproducir sólo las dos primeras octavas del espectro, o sea, de 20Hz a 80Hz o a lo sumo 120Hz, banda que los woofers y mid-woofers normalmente no reproducen bien.
Como dijimos antes, hay otros tipos de transductores acústicos, pero son minoría, como los paneles electroestáticos y los diferentes tipos de tweeters mencionados. En la web hay cientos de paginas con información si les interesa. Nnosotros nos dedicaremos solamente a los transductores “electroacústicos” que ocupan más del 90% del mercado.
Bueno ya tenemos una idea de cómo funcionan y por qué hay varios altavoces en un equipo de música, pero hay un detalle que no hemos nombrado. ¿Por qué siempre están dentro de una caja de madera (o plástico si son baratos) y no al aire libre? ¿Por qué esta caja es de diferente tamaño dependiendo del altavoz que contenga? ¿Qué son esos agujeros que tienen normalmente?
Responder a estas preguntas será el tema del próximo artículo. ¡Que lo disfruten!
- Para más información, aquí. [↩]
- Hay muchísimos woofers de estos tamaños que reproducen hasta más de 2000Hz, pero no de forma fiel, por eso no los tomamos en cuenta. [↩]
- El ancho del bafle también influye en esto, pero será tema de todo un articulo. [↩]

The La reproducción de la música y los sonidos. “Tipos de altavoces” by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.








{ 22 } Comentarios
“Nuestro oído puede detectar sin problemas una variación de 60Hz a 61Hz, pero no de 10000Hz a 10001Hz ya que nuestro oído también trabaja de forma logarítmica”.
Cada octava es el doble de frecuencia (el doble de Hz que la anterior), se trata claramente de una progresión geométrica y no de un logaritmo. Tiene más que ver con esto que con que el oído funcione de forma logartmica, creo yo.
Lo pensaba explicar en mi serie cuando llegáramos a las notas y las escalas:
Una octava tiene doce semitonos. Si a1=440Hz, a13 (que es su octava, doce semitonos más que a1) =880Hz.
Teniendo en cuenta que an=a1*r^(n-1), tenemos que la razón de la progresión geométrica es r=(an/a1)^-(n-1), es decir, r=(880/440)^-12, o, lo que es lo mismo, la raíz duodécimsa de dos.
Bueno, pensándolo bien, el término general de una progresión geométrica es a1 multiplicado por una exponencial cuya base el la razón de la progreción… El logaritmo es la función inversa de la exponencial. Seguramente son dos formas diferentes de explicar lo mismo
Hola compotrigo, creo que estamos hablando lo mismo pero explicado de dos maneras, la científica, y la simple, como es una introducción preferí la simple. Igual cuando lleguemos al tema de distorsiones vamos a empezar a ver temas complicados y muy interesantes y ahí si vamos a interiorizarnos mas, pero necesito que se entienda la idea antes para no comernos el tortazo de una.
Saludos
De todas formas, después de pensarlo (que me corrija alguien, por favor), creo que no es científicamente incorrecto decir que el oído percibe el tono logarítmicamente: para percibir cada octava más aguda el oído necesita un incremento exponencial de la frecuencia (dado por una progresión geométrica), luego es como si oyera un logaritmo (inversa de la exponencial) de la frecuencia.
Podemos hacerlo más fácil aún olvidándonos de los semitonos. Si trabajamos simplemente con octavas (cada octava el doble de frecuencia que la anterior), una octava n (On) equivaldrá en frecuencia a la primera octava (O1) multiplicada por dos elevado a n-1.
On=O12^(n-1), así, O2=O12, O3=O12^2, O4=O12^3, O5=O1*2^4 y así sucesivamente.
Para saber n (el número de octava) le haríamos el logaritmo en base 2 a la potencia de 2 y le sumaríamos 1, ¿no?
“¿Qué pasa cuando la longitud de onda empieza a ser menor que el diámetro del altavoz? Pues sucede un efecto llamado “difracción por borde” y el altavoz entra en una transición de emitir cada vez más direccionalmente hacia delante. Esto tiene dos problemas: uno es que si nos ponemos justo delante del altavoz escuchamos bien todo, pero si nos movemos a un lado, escuchamos sólo las frecuencias cuyas longitudes de onda son mayores que el diámetro, y las menores, no, y segundo, como antes la energía la distribuíamos esféricamente en todo el espacio circundante, a cada punto llegaba cierta cantidad que obedecía a la regla “disminuye con el cuadrado de la distancia”, pero ahora que el altavoz esta radiando sólo hacia adelante, ¡concentra toda la energía en una dirección!, haciendo que en ese punto los sonidos cuya longitud de onda es menor que el diámetro del altavoz suenen mucho más “fuerte” o sea, con mayor presión sonora.”
Esto que cuentas es muy fácil de comprobar empíricamente. Si te vas a una tienda, un centro comercial o cualquier lugar que tenga los altavoces en el techo y apuntando hacia abajo (por ejemplo, esos con rejilla redonda empotrados horizontalmente en la escayola del techo), sólo tienes que colocarte justo debajo del altavoz, en su misma vertical, para oír muchísimo mejor los agudos (que tienen menor longitud de onda), si te mueves a penas un par de pasos hacia cualquier dirección, de repente, sigues oyendo perfectamente la música, pero la oyes como si estuviera ecualizada de otra forma, muchos de los agudos que antes oías nítidamente ahora desaparecieron Yo no sabía que esto se debía exactamente al efecto que describes en tu artículo. Siempre había escuchado que los sonidos agudos son más direccionales y los graves más omnidireccionales, pero pensaba que era cosa de la naturaleza misma del sonido y no de los altavoces. No te acostarás sin saber una cosa más (sobre todo si lees El Tamiz y El Cedazo).
Yo no sabía que esto se debía exactamente al efecto que describes en tu artículo. Siempre había escuchado que los sonidos agudos son más direccionales y los graves más omnidireccionales, pero pensaba que era cosa de la naturaleza misma del sonido y no de los altavoces. No te acostarás sin saber una cosa más (sobre todo si lees El Tamiz y El Cedazo).
¡Ay!, en el comentario 4 quise decir:
On=O12^(n-1), así, O2=O12, O3=O12^2, O4=O12^3, O5=O1*2^4 y así sucesivamente.
No me salen todos los asteriscos (multiplicaciones)…
On=O1 * 2^(n-1), así, O2=O1 * 2, O3=O1 * 2^2, O4=O1 * 2^3, O5=O1 * 2^4 y así sucesivamente
¡Que lió has hecho con la ecuación! pero entiendo a lo que quieres llegar, y si, el oído percibe el sonido de forma logarítmica. Saludos
Lo sé, me repito, pero me encantan vuestras dos series.
Compotrigo, de hecho, decir que el oido trabaja de forma logarítmica es la forma científicamente correcta de hacerlo, y es exáctamente lo que decías en tu primer comentario
De la wikipedia (http://es.wikipedia.org/wiki/Ley_de_Weber-Fechner): “La relación entre el estímulo y la percepción corresponde a una escala logarítmica. Esta relación logarítmica nos hace comprender que si un estímulo crece como una progresión geométrica (es decir multiplicada por un factor constante), la percepción evolucionará como una progresión aritmética (es decir con cantidades añadidas).”
Sin más, decir a juanfilas que me está impresionando. Cuando vi el inicio de la serie no pensaba que fuese a ser ni tan interesante, ni tan didáctica. Muchas gracias!
Siempre soñe con que algun dia podria hacer mis propias cajas y que estas serian de la mejor calidad, debido a lo que estoy aprendiendo en tu serie de articulos no tengo ninguna duda en que lo conseguire, seguire con muchisima atencion los articulos por venir, recibe mi mayor respeto por tus grandes conocimientos y todo mi agradecimiento por tener la capacidad de compartirlos, un fuerte abrazo a la distancia para ti Juanfilas
“Compotrigo, de hecho, decir que el oido trabaja de forma logarítmica es la forma científicamente correcta de hacerlo, y es exáctamente lo que decías en tu primer comentario “.
Alberto, en mi primer comentario pensé en una progresión geométrica sin caer en la cuenta de que el término general de este tipo de progresiones es una exponenciación (operación inversa al logaritmo). Por eso, después de pensar un poco más, hice mi segundo comentario.
He leído la ley que citas y enlazas, no la conocía. ¿De verdad es aplicable a todos los tipos de estímulos? De todas formas, me da la sensacion de que la ley de Weber-Fechner sólo hace referencia a la intensidad de los estímulos y no a la frecuencia. Yo ya tenía claro que la intensidad del sonido se percibe de forma logarítmica, de ahí que se mida en decibelios, una unidad logarítmica. Pero aquí estábamos hablando de la frecuencia del sonido, no de la intensidad.
Hay otras cualidades del sonido que no se me ocurre la forma de relacionar con un logaritmo, por ejemplo, el timbre. Que yo sepa no existe una unidad de timbre… A ver cómo relacionas lo que varía la forma de onda de un sonido y la variación de percepción en el timbre que experimenta el oído al hacerlo con un logaritmo (aunque a lo mejor calculando la pendiente que describe la curva en cada punto… Pero ya me salgo mucho de mi campo).
Otra cosilla, juanfilas, en el próximo artículo de mi serie ha pensado en escribir algo sobre tipos de micrófonos, generalidades sobre cómo se mezcla las diversas fuentes de onido en el estudio y cosillas así. Si te parece bien, cuando tenga el artículo listo, te escribo un mensaje interno por si lo quieres leer antes de su publicación y así me dices si hay algo que corregir o si añadirías o quitarías cualquier cosa.
Un saludo.
@ Trendelas4: Por supuesto que vas a poder armar tus propios altavoces, lo único es que vas a tener que esperar bastante ya que todavia falta un artículo introductorio y luego empezamos con los mas complejos.
@Compotrigo: no vas a lograr relacionar el timbre con un logaritmo ya que el timbre es una percepción SUBJETIVA nuestra, no existe tal cosa en la realidad física, es simplemente como nuestro cerebro suma ondas armónicas a través del tiempo e interpreta que es una sola, pero en la realidad no hay un “timbre” característico sino un montón de ondas a distintas frecuencias, ya lo vamos a tratar en el artículo de las distorsiones.
Habla todo lo que quieras de micrófonos ya que me ayudas a mi y por supuesto que no tengo problemas en revisarlo y ver si añadís o quitas algo, acá hacemos ciencia entre todos.
y por supuesto que no tengo problemas en revisarlo y ver si añadís o quitas algo, acá hacemos ciencia entre todos.
@Alberto y Laertes: gracias por sus comentarios, se que cuando dejemos las introducciones y empecemos a ver temas mas complejos les va a gustar más.
Saludos
No, si no es que yo quiera relacionar el timbre con un logaritmo. Lo que yo quería decir es que si afirmamos, sin especificar, que el oído trabaja de forma logarítmica, se podría interpretar que todo (la altura, la intensidad, la duración, el timbre) lo percibe de forma logarítmica (y, que yo sepa, no hay forma de relacionar la percepción del timbre o la de la duración de un sonido con un logaritmo, por eso dije que no se me ocurría la forma de relacionar el timbre con un logaritmo, no porque yo quiera hacerlo, sino porque creo que no se puede hacer). A lo mejor es que en estas cosas soy muy puntilloso, pero simplemente quería señalar que soy partidario de precisar lo más que se pueda el lenguaje que se utiliza cuando se habla de asuntos técnicos.
Un saludo. Y gracias por tu disposición a ayudar.
Después de releer el artículo se me ha ocurrido una pregunta, ¿Cómo hacen los altavoces de los auriculares para reproducir los graves adecuadamente siendo tan pequeños? Me refiero a auriculares de calidad claro, en los de 1€ no hay graves por ningún lado.
Hola Laertes, en realidad todos los altavoces reproducen toda la gama de frecuencias, el tema es a que sensibilidad (tema que trataremos en el futuro). Pero hasta un tweeter reproduce graves solo que a un volumen muchìsimo menor, tanto por el tamaño y por su diseño, ademas que si aumentas la potencia lo quemas si le entregas graves. En un auricular el altavoz esta hecho de forma que reproduce todos las frecuencias al mismo volumen ajustando la curva con una bobina (con la mismas sensibilidad) pero la sensibiliadad final es bajìsima, como estan pegados a tus oidos lo oyes perfectamente, y como la potencia que le entregas es muy baja (del orden de mW) no tienes problemas. ¿se entendio?
Saludos
Entendido, ¡muchas gracias! Ya me imaginaba que al estar pegados al oido no tenían tantos problemas.
Hola juanfilas!
Enhorabuena por tus publicaciones, están la mar de interesantes.
Me ha traído de cabeza ese extraño fenómeno de la relación diámetro del altavoz-longitud de onda. Podrías recomendarme algún libro que venga completito sobre el tema? Características del sonido, comportamiento, fenómenos, altavoces, etc. me gustaría profundizar en esos aspectos técnicos
Gracias!
Magnifico post, muchas gracias!! ^^
Muy buenas tardes, me ha encantado el articulo, me ha aportado mucho. Quisiera saber si tendrá usted una vieja tabla que habla de la relación entre el tamaño en pulgadas del altavoz y la capacidad de este para llegar a reproducir fielmente bajas frecuencias. Creo recordar que para reproducir bien los 20 Hz necesitabas un altavoz de 20″ (50cm). Si me hace el favor de compartirla? Muchas gracias.
De mucha utilidad éste articulo. Debido a ello pude construir un crossover para mis midranges teniendo en cuenta en las pruebas y ensayos las frecuencias de las voces e instrumentos musicales. Muchas gracias.
Escribe un comentario