En el primer artículo de Eso que llamamos “Música” (A propósito del sonido), vimos que los sonidos proceden de cuerpos que vibran. Estas oscilaciones se transmiten de dichos cuerpos al medio elástico que los rodea (en nuestro caso, el aire). Una vez en el medio, los sonidos se propagan a través de éste como ondas sonoras (por cierto, he encontrado este interesante enlace que a más de uno nos ayudará a hacernos una mejor representación mental del sonido).
Recordarás que estas ondas sonoras pueden tener mayor o menor amplitud (oscilaciones más o menos amplias), mayor o menor frecuencia (oscilaciones más o menos rápidas), distintas formas de onda y, además, se pueden sumar. Ahora trataremos de mostrar cómo afecta todo esto al sonido que percibimos.
Me propongo en el presente artículo que veáis y escuchéis múltiples ejemplos de sonidos con distintas características. Por eso, tal y como avanzábamos en el anterior capítulo de esta incipiente serie (lo prometido es deuda, amigo lector), he aquí el momento, para comprender mejor el hecho sonoro, de introducir los parámetros del sonido que nos interesan en Música, es decir, las características más relevantes del sonido.
Parámetros del sonido
Los parámetros o características básicas del sonido son: altura, duración, intensidad y timbre. A continuación los veremos uno por uno de forma detallada.
Duración
Ya que desde que expusimos nuestra definición (música es “el arte de combinar los sonidos y el tiempo para deleite del oído”), no hemos hablado del tiempo, permitidme que comience por el parámetro de la duración.
No creo que haya muchos problemas en entender que en Música algunos sonidos suenan antes en el tiempo y otros después. También podemos hacer que una melodía sea más rápida o más lenta, pero refiriéndonos al tiempo en un sonido aislado, en principio, sólo podemos apreciar si dicho sonido es más corto o más largo.
Esto no tiene mucho que comprender: hay instrumentos que, por su naturaleza, sólo pueden producir sonidos cortos (por ejemplo, cuando golpeamos unas claves sólo oímos su sonido durante un instante). Otros instrumentos, por el contrario, nos permiten producir sonidos durante un período de tiempo más largo. Nótese que si apretamos una tecla del órgano de una iglesia, éste producirá un sonido, y continuará produciéndolo mientras mantengamos la tecla pulsada. Fíjate: si apretamos la tecla durante mucho rato, produciremos un sonido largo; mientras que si apretamos esa misma tecla durante poco tiempo, el instrumento emitirá un sonido idéntico, pero corto. Lo mismo pasa si soplamos una flauta dulce: podemos soplar una nota durante una fracción de segundo o estar soplando hasta que se nos agote el aire.
Evidentemente, este parámetro del sonido, la duración, se identifica en nuestras representaciones gráficas de ondas sonoras con el tiempo. Es decir, un sonido corto (de escasa duración) se extenderá poco en el eje horizontal (tiempo), mientras que un sonido largo ocupará una mayor región de dicho eje.
Observa cómo en estas imágenes la onda de dos segundos llega “más lejos” en el eje horizontal que la de un segundo.
Pero corto y largo son términos relativos. Por ello, la duración objetiva de un sonido concreto puede medirse, tal y como hemos visto, en segundos o fracciones de éstos. Sin embargo, en Música, lo que se suele hacer es representar el tiempo que dura cada sonido con las distintas figuras (redonda, blanca, negra, corchea…), que ya explicaremos en otro artículo de la serie. Cada una de estas figuras tiene una duración que guarda una determinada proporción con la duración de la anterior, de modo que no se suele expresar la duración en términos absolutos, sino proporcionales.
Intensidad
Otro parámetro del sonido que no tiene mucha historia es la intensidad. Prácticamente podemos identificar la intensidad de un sonido con la amplitud de su onda sonora: si aporreo muy fuerte un tambor, sonará muy fuerte porque la onda tendrá mucha energía y, por consiguiente, una gran amplitud. Si toco con menos fuerza, la onda resultante tendrá menor amplitud y, por tanto, el sonido tendrá menor intensidad, sonará flojito.
Escucha el sonido con poca intensidad.
Escucha aquí el mismo sonido con mucha intensidad.
Fuerte y flojito son también términos relativos. Podemos medir la intensidad de un sonido de forma objetiva en decibelios. En realidad, como bien me indica J, los decibelios son una medida relativa, dado que se miden tomando como referencia el límite de audición humano, al que se asigna el valor 0dB. Aunque están tomados de forma arbitraria, si continuáis leyendo el artículo encontraréis la definición de decibelio de la Wikipedia. Allí se menciona claramente el decibelio como medida de la relación entre dos magnitudes.
Y, ojo, quisiera hacer un inciso importante: las ondas sonoras de gran intensidad son muy peligrosas, más de lo que imaginamos. A determinadas intensidades de sonido, nuestros órganos internos pueden sufrir daños. Imagina, por ejemplo, que un ruido con más decibelios que el de los reactores de un avión podría llegar a matarte…[1]
Pero eso no es todo, no somos conscientes de que perdemos audición por momentos. Vivimos en una sociedad muy ruidosa, y hacemos bien poco por mejorar esto. Por si no bastase el ruido del tráfico o el de las obras municipales, tendemos a hablar muy fuerte, mucho más de lo que es necesario para asegurar la comunicación. ¿Quién no ha entrado en un bar repleto de gente donde el mismo griterío (y digo «griterío» y no «murmullo» porque tendemos a conversar a gritos) de las personas nos obliga a elevar el volumen de la voz? Si hay multitud de conversaciones simultáneas tenemos dos opciones:
a) Hablar todos con el volumen de voz suficiente como para que nos oiga nuestro interlocutor, pero sin que sea tan fuerte como para que dificulte la conversación del «vecino».
b) Hablar muy fuerte, por encima de las voces de todos los demás, para que, por mucho ruido que haya, a nuestro interlocutor le lleguen nuestros gritos de forma inteligible sin que estorben demasiado los gritos de los demás.
¿Cuál de estas opciones solemos elegir de forma inconsciente? Pues eso.
En una ocasión, por curiosidad, realicé una medición del nivel de decibelios que había en un bar: 90 decibelios (y no había música puesta en el local, se trataba sólo de las múltiples conversaciones simultáneas). Por encima de 80 u 85 decibelios empieza a existir riesgo de pérdida de audición. Es más, quince minutos a esa intensidad de sonido pueden provocar pequeñas pérdidas auditivas permanentes de las que puede que no te des ni cuenta, pues la pérdida de audición en frecuencias altas[2] no dificulta la comunicación[3]. Y, aunque no te des cuenta, estas pequeñas pérdidas se van sumando con el paso del tiempo. Piensa en ello.
Sobre la intensidad del sonido no me queda mucho que decir. Sólo, tal vez, que no siempre oímos todos los sonidos de igual amplitud con la misma intensidad: hay frecuencias que, a igual amplitud que otras, el oído humano (y algunos oídos más que otros) percibe con mayor intensidad. Además he leído que hay otros factores psicoacústicos que influyen en la percepción de la intensidad de los sonidos, pero yo no los conozco bien, así que no voy a hablar de ellos.
Otra cosilla más: hemos visto que la intensidad sonora se mide en decibelios. Si te paras a pensar, puede que no te resulte demasiada la diferencia entre la intensidad de una multitud ruidosa (90 dB) y el ruido de un avión en marcha (120 dB), por ejemplo. Tal vez te parecezca que 30 dB no es demasiado, pero debes pensar que el decibelio es una unidad logarítmica.
Si te fijas en la gráfica de un logaritmo, verás que describe una curva a la que, conforme va creciendo, ”le cuesta más” crecer. Es decir, si estuviésemos en un ambiente relativamente silencioso (unos 10 dB, por ejemplo), no nos costaría demasiado elevar dicho ambiente a los 40 dB.
Sin embargo, si estamos en medio de una pista de un aeropuerto justo cuando tiene lugar un despegue, necesitaríamos algún artefacto que nos permitiera producir un ruido verdaderamente brutal (y nada recomendable), probablemente el mayor ruido de tu vida, para elevar los niveles sonoros de 130 dB a 160 dB.
Corto y pego de la Wikipedia aquello en lo que creo que merece la pena hacer énfasis:
“Decibelio es la unidad relativa empleada en acústica y telecomunicaciones para expresar la relación entre dos magnitudes [...]
El decibelio, cuyo símbolo es dB, es una unidad logarítmica. Es un submúltiplo del belio, de símbolo B, que es el logaritmo de la relación entre la magnitud de interés y la de referencia, pero no se utiliza por ser demasiado grande en la práctica, y por eso se utiliza el decibelio, la décima parte de un belio [...]
Un belio equivale a 10 decibelios y representa un aumento de potencia de 10 veces sobre la magnitud de referencia. Cero belios es el valor de la magnitud de referencia. Así, dos belios representan un aumento de cien veces en la potencia, 3 belios equivalen a un aumento de mil veces y así sucesivamente.
El decibelio es la unidad de medida utilizada para el nivel de potencia y el nivel de intensidad del ruido
Se utiliza una escala logarítmica porque la sensibilidad que presenta el oído humano a las variaciones de intensidad sonora sigue una escala aproximadamente logarítmica, no lineal [...]
Se define como la comparación o relación entre dos sonidos porque en los estudios sobre acústica fisiológica se vio que un oyente, al que se le hace escuchar un solo sonido, no puede dar una indicación fiable de su intensidad, mientras que, si se le hace escuchar dos sonidos diferentes, es capaz de distinguir la diferencia de intensidad“.
Quede claro entonces que los decibelios (y los belios, claro) son siempre una relación entre dos magnitudes. Es decir, desde el punto de vista estricto matemático, es incorrecto decir “este sonido es de 14dB”, porque los dB solo indican la diferencia entre una magnitud y otra. Y entonces, ¿por qué en sonido decimos “este sonido es de 14dB”? Lo que se hace es definir un sonido de referencia y medir todos los sonidos con respecto a ese. Ese sonido de referencia se define como el umbral que el ser humano es capaz de oír (obviamente, depende del ser humano en cuestión, pero bueno, se define uno). Por lo tanto, en lenguaje coloquial decimos “el sonido de referencia tiene 0dB” y “esta guitarra suena con 35dB”, cuando desde el punto de vista estricto deberíamos decir “esta guitarra suena 35dB más fuerte que el sonido de referencia”… pero cuando estamos hablando de sonido, todo el mundo entiende que “X dB” significa en realidad “X dB más que el umbral de audición humano”.
Quede claro también que los dB son una medida logarítmica (en base diez): 10 dB (es decir, un belio) más significa multiplicar por 10. Así, aumentar de cero a diez decibelios supone multiplicar por diez una intensidad relativamente pequeña (nuestro umbral de audición), mientras que aumentar, por ejemplo, de diez a veinte decibelios (un belio más) supone volver a multiplicar por diez, esta vez, una intensidad diez veces mayor que nuestro umbral de audición… Conclusión: la medida, aunque objetiva, es relativa, ya que depende de la relación entre dos magnitudes.
¿Y por qué usamos una medida logarítmica para medir la intensidad del sonido? Es una de las pocas medidas que habitualmente usamos logarítmicamente. Esto es porque el oído humano también funciona más o menos logarítmicamente: hace falta un incremento exponencial de la intensidad del sonido para que el oído humano note el cambio.
Por si no termina de quedarte claro esto de que percibimos la intensidad del sonido de forma logarítmica, puedes echarle un vistazo al vídeo del final del artículo. Allí presentamos un mismo sonido con nueve niveles de intensidad ordenados (cada vez más fuerte). Lo hemos hecho de forma que los incrementos de amplitud son siempre iguales entre sonidos sucesivos (es decir, siempre aumentamos lo mismo la amplitud). Sin embargo, puedes notar perfectamente que entre los niveles 1 y 2 se percibe mucha diferencia, mientras que entre los niveles 8 y 9 se nota bastante menos (insisto: a pesar de que la diferencia de amplitud es la misma en todos los casos).
Un último inciso que quisiera hacer con respecto al parámetro de la intensidad: notará el lector que a veces utilizo el término volumen como sinónimo de intensidad. No me parece del todo incorrecto este uso (sobre todo por no andar repitiendo siempre el mismo vocablo), ya que cuanto mayor es la intensidad, mayor resulta el volumen. Pero volumen en Psicoacústica (y yo ya en este terreno me pierdo) es la percepción subjetiva de la potencia de un sonido. También en Psicoacústica, la percepción subjetiva de la intensidad se denomina sonoridad. Curiosamente, tanto volumen como intensidad son medidos en decibelios.
Altura
El tercer parámetro que abordamos es el de la altura. La altura de un sonido viene dada por la frecuencia de vibración de su onda, es decir, su número de oscilaciones por segundo. Cuanto mayor es la frecuencia de un sonido (cuanto más rápido vibra), más agudo lo percibimos; a menos frecuencia, decimos que el sonido es más grave. Podemos medir objetivamente la frecuencia de un sonido en hercios (Hz).
Debemos hacer aquí una distinción: hay sonidos que vibran de una forma suficientemente regular, así emiten una nota musical fácilmente distinguible (tono); mientras que la vibración irregular de otros sonidos hace imposible a nuestro oído identificarlos con las notas musicales.
A los instrumentos musicales que emiten sonidos con tono los llamamos instrumentos de sonido determinado, y son todos los instrumentos melódicos (flauta, violín, clarinete…) y armónicos (piano, guitarra…).[4]
En cambio, a los instrumentos que no producen notas musicales los llamamos instrumentos de sonido indeterminado, siendo la mayoría de ellos instrumentos de percusión (bombo, caja, platos, timbales, claves…); pero ojo: ¡no hay que confundirlos con los instrumentos de percusión con sonido determinado, como el xilófono o los metalófonos, que sí producen notas musicales!
Así pues, cuando decimos que nos queremos bajar un tono para el móvil,[5] en realidad, no nos referimos a un tono, sino a una melodía, o puede que a una melodía acompañada (o, qué demonios, incluso un contrapunto) si nuestro móvil es polifónico.
¿Y de qué depende entonces la frecuencia con que vibra un sonido musical? Pues depende principalmente:
1) De las dimensiones del objeto vibrante. Los instrumentos que suenan más grave son los más grandes; por el contrario, construimos los instrumentos agudos de menor tamaño. Así, una columna vibrante de aire, dentro de un instrumento de viento, emitirá un sonido más grave cuanto más grande sea dicha columna, o una cuerda más gruesa emitirá un sonido más grave que otra más fina (en igualdad del resto de condiciones: tensión, longitud y material).
Una cuerda más larga también emitirá un sonido más grave que otra que tenga la misma tensión, grosor y esté hecha del mismo material. De hecho, una vez fijadas el resto de características de la cuerda, la longitud de la misma es inversamente proporcional a la frecuencia. O sea, una cuerda de cierta longitud producirá una nota del doble de frecuencia que otra cuerda con el doble de longitud (doble longitud, mitad de frecuencia; mitad de longitud, doble frecuencia). Por esta razón, un violinista puede emitir distintas notas con cada cuerda de su violín, sólo tiene que colocar el dedo en el punto justo para acortar la longitud del segmento de cuerda que hace vibrar de forma que lo haga con la frecuencia exacta de la nota musical que quiere que suene.
Por fin, una misma cuerda vibrará más rápido (su sonido será más agudo) cuanto mayor sea la tensión a la que está sometida. Ése es el principio por el que se rige, por ejemplo, el clavijero de afinación de una guitarra.
Es muy fácil también que los instrumentos se desafinen con los cambios de temperatura, ya que los materiales de que están hechos se dilatan y se contraen. Lo que ya no sabría yo decir es cuánta puede ser la influencia de la temperatura del aire en la frecuencia de una onda y en su velocidad de propagación… (¿algún físico en la sala?).
2) Del tipo de material del que está hecho el objeto vibrante (e intuyo que de la densidad del mismo). Por ejemplo, si golpeamos un trozo de madera (podría ser una lámina de un xilófono) obtendremos una nota musical más grave que si golpeamos un bloque de metal del mismo tamaño (que podría ser una placa de un metalófono). Esto se debe a que el metal vibra más rápidamente que la madera (supongo que por el hecho de ser más denso).
3) De la tensión, como ya hemos mencionado, en caso de ser una cuerda el objeto vibrante.
Los siguientes ejemplos que te mostramos son ondas iguales en todo (duración, amplitud, y timbre) excepto en la frecuencia. Cien vibraciones son muchas para verlas en la pantalla, así que hemos tomado la imagen de una centésima de segundo (0,01 s) de cada onda. La frecuencia de 100 Hz vibra cien veces cada segundo, si tomamos una centésima de segundo…
Escúchalo: Sonido de 100 Hz.
Escúchalo: Sonido de 500 Hz.
Escúchalo: Sonido de 1000 Hz
A pesar de tener la misma amplitud, hay frecuencias que oímos más fuerte que otras. Cada persona tiene su propia curva de audición. Como vemos, la percepción psicoacústica de la intensidad depende no sólo de la amplitud (aunque un mismo sonido sonará con más intensidad cuanto mayor sea la amplitud), sino también de la frecuencia (y de otros factores): bien en el centro (1-2kHz) y cada vez peor en los extremos, hasta que llega un punto, por arriba y por abajo, en que ya no oímos.
Y, por cierto, el dispositivo en que reproducimos estos sonidos tampoco es perfecto, cada modelo de altavoz tiene distinta respuesta a determinadas frecuencias, con lo que pueden sonar unas más fuerte que otras.
De hecho, lo normal es que los altavoces no suenen igual en todas las frecuencias (salvo que se trate de altavoces con respuesta plana como los que usan los técnicos e ingenieros de sonido en los estudios de grabación), de modo que los sonidos grabados que son reproducidos en ellos no suenan exactamente igual que los originales.
Otra cosilla sobre la altura es que cuando hablamos de tener oído musical, básicamente nos referimos a la capacidad de reconocer de forma precisa variaciones en la altura (incluso si son muy pequeñas), darse cuenta de si un sonido está bien afinado o no, reconocer diferentes patrones melódicos, etc.
Hay personas (pocas) que tienen lo que se llama oído absoluto. Estas personas son capaces de distinguir la altura absoluta de cualquier nota musical. Es decir, si escuchan un sonido musical aislado saben automáticamente si se trata de un do, un re, un mi, o lo que sea; pero no sólo eso, sino que además se dan cuenta de si está afinado en tono de concierto (con el la 440 Hz) o en cualquier otra afinación. Desconozco la sensación que deben tener al identificar así los sonidos sin necesidad de referencia alguna.
Tener oído absoluto es relativamente poco común. Dicen que es una cualidad innata que se tiene o no se tiene y que no se puede entrenar; aunque también dicen que los pianistas, como siempre tocan en un piano afinado en tono de concierto[6], con el tiempo, llegan a memorizar la altura absoluta de las notas.
De todas maneras, el oído absoluto no es algo ni mucho menos imprescindible para un músico. Es mucho más útil el oído relativo. También hay personas que nacen con mejor y peor oído relativo, pero éste se puede educar mediante el trabajo (aunque, como en todo, siempre habrá quien tenga mayor o menor facilidad para ello).
Por cierto, ya que os he hablado del oído absoluto, os voy a comentar una curiosidad que oí de Steve Vai, uno de mis guitarristas de rock favoritos.[7] Dicen que hubo una época en la que Vai, además de practicar unas catorce horas diarias, dormía con unos auriculares puestos que emitían un sonido continuo afinado a 440 Hz, supuestamente para ganar oído absoluto. Desconozco si con este sistema obtuvo buenos resultados…
Los músicos hacen dictados melódicos para potenciar su oído relativo. El profesor les da una nota de referencia (que puede ser el la 440) con el piano, con un diapasón, entonando con su voz… y a partir de ahí van sonando primero notas, luego intervalos y más tarde melodías completas, que el estudiante debe reconocer sólo con el oído y después escribir.
Nótese que una persona con oído absoluto no necesitaría que le diesen una nota de referencia. Sabría perfectamente qué nota está sonando en cada momento. Sin embargo, una persona con oído relativo sabe que, si esta nota es la, entonces la siguiente nota que ha sonado en el dictado es do, por ejemplo. Pero si la primera nota no fuese la, sino que fuese la sostenido, entonces la segunda nota sería do sostenido; y si la primera nota fuese si, la segunda nota sería re… Es decir, una persona con oído relativo no conoce el valor absoluto de las notas, pero sí distingue perfectamente las distancias relativas entre ellas.
Estos dictados, junto con el ejercicio de la entonación, mejoran la “audición interior” de los músicos. Es decir, un músico bien entrenado es capaz de oír en su cabeza una partitura sólo con leerla, y reproducirla cantando aunque no la haya escuchado jamás. Un ejemplo de una audición interior extraordinaria lo tenemos en Beethoven, que tras quedarse sordo fue capaz de componer obras sinfónicas (¡¡¡oyendo dentro de su cabeza cómo sonaban todas las voces de todos los instrumentos de la orquesta a la vez!!!).
Por último, podríamos hacer también una distinción entre oído melódico y oído armónico. Con el oído melódico los músicos distinguen las notas, por así decirlo, de una en una (no hay más de una nota sonando al mismo tiempo). Pero ellos también se entrenan haciendo dictados armónicos, en los que suenan varias notas a la vez y se trata de reconocer las distintas especies de acordes (acordes mayores, menores, disminuidos, de séptima dominante…) que suenan sin verlos escritos en la pauta. Y no sólo el tipo de acorde, sino la inversión y la disposición que presentan.[8]
El timbre
En cuanto al timbre, puede que resulte el aspecto más “misterioso” de un sonido. Normalmente nos dicen que cada instrumento tiene un timbre, un “color” que es lo que nos permite distinguir su sonido del de otros, pero no nos suelen dar mayores explicaciones…
El timbre depende, básicamente, de la forma de onda. En el anterior capítulo de nuestra serie, vimos que las ondas pueden sumarse. Confío en que todos podamos entender que, lógicamente, de igual modo que varias ondas simples sumadas dan lugar a una onda más compleja, toda onda compleja puede descomponerse en un conjunto de ondas simples. Sobre esto, nuestro buen amigo J nos dirá algo más al final de este epígrafe.
Pues sí, compañeros, casi todos los sonidos musicales son, de hecho, complejos; sus ondas sonoras son ondas compuestas que se pueden descomponer en otras más simples. En el artículo “a propósito del sonido” tuvimos la oportunidad de conocer formas de onda simples, tú mismo podrás comprobar a continuación que el sonido de una onda senoidal es como el pitido que acompañaba a las antiguas cartas de ajuste de la tele. Y, como podrás imaginar, el sonido rico de un instrumento musical depende, generalmente, de una forma de onda mucho más compleja.
Si quieres oír sonidos con formas de onda básicas, aquí tienes tres sonidos iguales en todo (amplitud, frecuencia y duración) salvo en la forma de onda. Escúchalos, verás cómo difieren sus timbres: onda senoidal, onda cuadrada, diente de sierra.
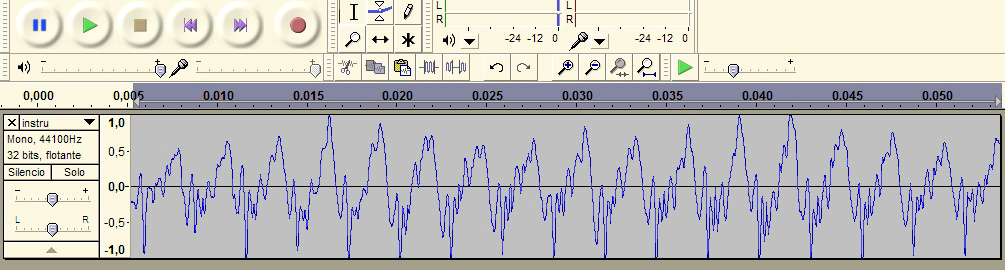
Los sonidos de los instrumentos reales son mucho más complejos porque tienen infinidad de armónicos. A continuación podemos ver cómo es la onda de un instrumento real: un saxo.
Y, por fin, lo que pretendemos conseguir ahora es descomponer un imaginario sonido complejo en sonidos simples: sus armónicos (o parciales). Si pensamos en una columna de aire vibrante ideal dentro de un instrumento de viento, o el movimiento ondulatorio de una cuerda ideal en un instrumento musical, vemos que existen no uno, sino varios movimientos periódicos (son los distintos modos de vibración, que los podría explicar un físico mucho mejor que yo). Podemos estudiar el movimiento de la cuerda en su longitud total, pero el de su mitad también resulta un movimiento ondulatorio completo, y así el de un tercio de su longitud, un cuarto, un quinto, un sexto…
Todos estos movimientos vibratorios ocurren a la vez y suenan a la vez. Los denominamos “la serie armónica”. La altura de los sonidos resultantes de los primeros movimientos de la serie corresponden, de manera más o menos precisa, a notas de la escala musical, y, conforme subimos más y más en la serie, aparecen sonidos más desafinados.
Digamos que “dentro” de una sola nota musical suenan más notas diferentes. Estas notas se denominan “armónicos” o “sonidos parciales”. Pero el cerebro no las reconoce como notas independientes, sino que reconoce el conjunto como un timbre determinado. Generalmente, el tono o nota musical que escuchamos en el sonido de un instrumento es el de la frecuencia más grave de entre las que componen la onda compleja.
Escucha cómo va cambiando el timbre de una onda senoidal de 200 Hz a medida que vamos añadiendo armónicos (todos ellos ondas senoidales múltiplos naturales de 200 Hz): sonido fundamental, añadimos el segundo sonido de la serie, añadimos el tercero y el cuarto.[9]
Según añadimos armónicos, el sonido se va haciendo más complejo. Mira la forma de onda de nuestro seno cuando le hemos añadido armónicos hasta llegar al sexto sonido de la serie:
Claro, hemos hablado de una cuerda ideal, o de una columna de aire ideal, pero los instrumentos no son ideales, tienen dimensiones, grosor, distintos materiales, etc. Por lo tanto, los armónicos de todos los instrumentos no son exactamente iguales a los de la serie armónica (algunos, como los de las campanas tubulares, son realmente diferentes a los de la serie, por lo que un simple acorde mayor tocado en estos instrumentos suena irreconocible).
En definitiva, los sonidos parciales de cada instrumento varían. En algunos instrumentos es característico que suene fuerte el segundo armónico, por ejemplo, otros, como el clarinete, carecen de él. Estas características permiten a nuestro cerebro distinguir los timbres de los distintos instrumentos (por eso reconocemos el sonido de un piano y lo distinguimos del de un violín). Vuelvo a enlazar aquí el artículo sobre la serie armónica de la Wikipedia porque me parece muy interesante su parte final (“el papel de cada armónico”) en la que nos explica qué armónico es responsable de cada característica del timbre (si suena más fuerte un determinado armónico, el timbre es más cálido, si suena más fuerte otro armónico, es más nasal…).
J ha tenido a bien escribir los siguientes párrafos para ilustrar el análisis espectral del sonido. Copio y pego:
“Se demuestra matemáticamente que cualquier forma de onda puede descomponerse en la suma de varias ondas senoidales de distintas frecuencias.[10] Cualquiera. Es lo que se denomina el espectro de la onda. En el caso general, ese espectro llega hasta frecuencias infinitas, pero habitualmente los componentes en frecuencias muy altas y muy bajas son despreciables, y como de todos modos no oímos fuera de una determinada banda de frecuencias…
Por ejemplo, una onda cuadrada perfecta como la que Compotrigo muestra más abajo, si es de 1kHz, es en realidad:  y así componentes cada vez más pequeñas y de frecuencia más alta hasta que simplemente podemos despreciarlas.
y así componentes cada vez más pequeñas y de frecuencia más alta hasta que simplemente podemos despreciarlas.
Más información en la Wikipedia.
Si lo pensáis con cuidado, y releéis ahora este epígrafe del timbre, veréis que todo lo de los armónicos, los modos de resonancia de la cuerda, los timbres, etcétera… todo encaja.”
Gracias, J.
Envolventes
Toca ahora hablar de envolventes.
Hasta este momento hemos visto ejemplos de sonidos cuyas características permanecían constantes desde que el sonido se originaba hasta que se apagaba. Sin embargo, los sonidos de los instrumentos reales pueden variar en el tiempo.
Vamos a fijarnos en la intensidad. Si pulsamos una cuerda de cualquier instrumento de cuerda, sonará una nota que, con el tiempo irá perdiendo intensidad hasta desaparecer. Si estudiamos el envolvente de volumen del sonido más detalladamente, nos daremos cuenta de que hay un corto periodo de tiempo en el que, desde que pulsamos la cuerda, se produce el sonido y éste va aumentando rápidamente de intensidad hasta alcanzar su máxima intensidad: es lo que llamamos ataque.
Después del ataque, hay otra fase (el decaimiento) en que el volumen del sonido decae hasta que se estabiliza. Una vez estabilizado, el sonido va perdiendo intensidad muy poco a poco, el volumen permanece casi constante. Ésta es la fase que denominamos sostenimiento (sustain). Si el instrumento en cuestión es capaz de producir sonidos muy largos, diremos que tiene mucho sustain, porque esta fase de su envolvente será muy larga. Por el contrario, si la cuerda deja de sonar pronto, quiere decir que esta fase es corta, por lo que decimos que el instrumento tiene poco sustain.
Por último, al final de la fase de sustain ocurre un relajamiento y el sonido se apaga. Os remito a este artículo si deseáis información más amplia.
Os dejo también un par de ejemplos de sonidos simples con envolvente de volumen (tal vez, más correctamente, envolvente de amplitud): ejemplo 1 y ejemplo 2.
Quisiera destacar aquí que el ataque de determinados instrumentos es una característica tan importante de los mismos que, si suprimimos dicho ataque, su timbre puede resultarnos irreconocible. En general, el envolvente propio de cada instrumento musical (los distintos tipos de instrumentos presentan envolventes distintos) nos ayuda también a reconocer su timbre, por lo que timbre y envolvente están íntimamente relacionados.
Pues bien, del mismo modo que el volumen o intensidad de un sonido puede variar en el tiempo, también lo puede hacer el tono, con lo que, de igual forma, hablaríamos de envolvente de tono.
Aquí tienes un sonido senoidal con amplitud constante y con un envolvente de tono, muy exagerado, tal que recorre todo el espectro audible (la frecuencia va aumentando desde los 20 Hz hasta los 20.000 Hz): escúchalo.
¿Otro ejemplo? Una onda diente de sierra que empieza con una frecuencia de 300 Hz y va subiendo gradualmente hasta los 1200 Hz para luego bajar a los 500 Hz (¡parece una sirena!): escúchalo.
Cualidades del sonido en la Armonía moderna
A modo de curiosidad, ya que hemos hablado del ataque, en algunos métodos de Armonía Moderna (de Jazz), se habla del ataque, el volumen y la densidad como cualidades del sonido.
El ataque depende de la intensidad del sonido, y también de la altura. Cuanto más intenso es un sonido, mayor ataque tiene. Cuanto mayor es la altura de un sonido, mayor ataque también. Un sonido con mucho ataque lo escuchamos como más “afilado”, más violento; la nota se “dispara” rápido, como una explosión.
El volumen del que nos habla la Armonía Moderna no se corresponde plenamente con la intensidad, pues si bien es una magnitud directamente proporcional a la intensidad, es inversamente proporcional a la altura. Es decir, los sonidos más agudos tienen menor volumen.
En cuanto a la densidad de un sonido, es directamente proporcional a la altura. Es decir, los sonidos más agudos, como ocupan menos volumen, son más densos.
He de decir que hasta hace un rato pensaba escribir aquí que, realmente, yo nunca he entendido muy bien esto de la densidad y el volumen en Armonía Moderna, pero creo que ahora, al tratar de explicároslo, se me ha iluminado la bombilla. Tengo la impresión de que lo que intentan algunos métodos modernos es definir el espacio que ocupa un sonido. Si pensamos en una longitud de onda pequeña (sonido agudo), ésta ocupa menos espacio (menos volumen) que una longitud de onda grande (sonido grave). Del mismo modo, a igual energía, los sonidos que ocupan menos espacio son más densos. Si no es así, que me corrija alguien que sepa de esto más que yo.
Sobre estos últimos conceptos, no quiero aburriros más con ellos. Simplemente me interesa que os suenen un poco, puesto que supongo que el público de El Tamiz y El Cedazo es muy variado y puede que haya gente que se interese aún más por este tema, le pique el gusanillo y busque información en manuales más técnicos y rigurosos; y, dependiendo de la fuente que consultéis, os podéis encontrar con esto del volumen y la densidad en vez de los parámetros clásicos del sonido (altura, duración, intensidad y timbre).
Si te has quedado con ganas de más, aquí tienes, a modo de resumen, este estupendo vídeo sobre los parámetros del sonido montado por Macluskey. Son apenas tres minutos. Que lo disfrutes:
Poco más que decir: hasta la próxima entrega, amigos; en ella profundizaremos aún más en el sonido y daremos fin a este primer bloque de artículos dedicados a la “materia prima” de la música.
- La fuente de esta información no es muy ortodoxa, pues recuerdo haberlo oído en un capítulo de «Los cazadores de mitos». [↩]
- Cuando el oído interno resulta dañado, se pierde primero audición en las frecuencias altas, ya que las células estereociliadas encargadas de detectar dichas frecuencias agudas, son más frágiles que las demás [↩]
- Mientras que un oído humano sano y perfecto es capaz de oír sonidos de 20 Hz a 20000 Hz, basta con oír bien hasta los 4000 Hz para apreciar correctamente la voz humana [↩]
- La diferencia entre instrumentos melódicos y armónicos estriba en que estos últimos son capaces de emitir más de un sonido simultáneamente. Por ejemplo: si pulsamos simultáneamente cuatro teclas de un piano, sonarán cuatro notas musicales a la vez. Dependiendo de cuáles sean estas notas, podremos considerarlas como un acorde. No te preocupes si las palabras acorde o armonía te suenan a Chino… En futuros capítulos les prestaremos a estos conceptos la atención que merecen. Lo importante aquí es que los instrumentos armónicos son capaces de generar, sin ayuda de otros, simultaneidad sonora. [↩]
- No me explico cómo se puede seguir ganando dinero con ese negocio, aunque parece que cada vez menos. Personalmente, no le veo el interés a ese tipo de cosas; sin embargo, ganancias sí que debe haber, al menos para costear la publicidad… [↩]
- No es como una guitarra o un violín, que se pueden afinar rápidamente como uno quiera, sino que el proceso de afinación de un piano es muy laborioso y lento (afinador de pianos es una profesión en sí misma) y el piano debe estar siempre listo. [↩]
- Para quien no lo conozca, Vai fue guitarrista en la banda de Frank Zappa. De él decía Zappa que era capaz de tocarlo todo. Es un ídolo para muchos, considerado un auténtico guitar-hero (que dirían los yanquis). Ciertamente es un guitarrista muy habilidoso que cursó estudios en el Berklee College of Music y que ha grabado numerosos discos. [↩]
- Esto último se refiere a la disposición que presentan las voces en el acorde, es decir, cuando estudiemos los acordes en el capítulo correspondiente, veremos que las notas do, mi y sol forman el acorde do mayor, no importa el orden en el que estén dispuestas las notas o la octava a la que pertenezca cada nota, cualquier combinación entre las notas do, mi y sol (do, sol, mi; mi, sol y do; mi, do y sol; sol, do y mi; sol, mi y do) forma un acorde de do mayor. Eso sí, para algunas cosas, en Armonía, sí es importante qué voz está en cada sitio (en el agudo, en el grave, en el medio…), lo veremos a su debido tiempo [↩]
- En realidad hemos hecho un pelín de trampa, sólo al sonido fundamental que hemos tomado le hemos dado mayor amplitud que al resto de armónicos. Cuando dediquemos un artículo a la serie armónica lo haremos de forma más fiel. En una serie armónica ideal, cada sonido parcial tiene la mitad de intensidad sonora que el sonido anterior; es decir, el quinto armónico tiene la mitad de volumen que el cuarto, la cuarta parte que el tercero… Por eso, los armónicos que aparecen muy tarde en la serie suelen tener poca importancia. [↩]
- En realidad en el caso general son exponenciales imaginarias, no senos, pero si necesitas llegar a ese nivel de finura es que no deberías estar leyendo esto, sino un texto más serio. [↩]

The Eso que llamamos “Música”: parámetros del sonido. by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.














{ 27 } Comentarios
Felicidades por el (los, en defiinitiva) artículos. Estoy disfrutando como un niño
Por cierto, el sonido de 100Hz ni lo oigo. Eso va a ser la edad, no?
me ha gustado mucho el artículo, sobre todo por que cuando he empezado a leer decibelios he pensao: “veras que hay algo mal” (perdón por pensar mal) y la verdad es que no, que está bien (o eso creo) y es raro por que los decibelios son lo suficientemente extraños como para meter la gamba en algún lado.
Total: Que me ha gustado mucho.
Este tema del sonido lo estudié en la universidad (ingeniero de telecomunicacion) y hablo de memoria pero os arrojo unos datos más sobre sonidos, pal que los quiera…. que si no los quereis pues na .
.
Hablo de memoria pero si no recuerdo mal, en temas de sonido la unidad de referencia del decibelio son 20 micropascales (que no sabía que se hubiera escogido por ser el mínimo que el oido podía escuchar) es una unidad de presión.
Para ponerlo en perspectiva: la presión atmosférica son 101.325 Pa a nivel del mar, que direis: bueno!!! anda que no queda.
Pero como has señalado, cada 10Db (que sumamos) es multiplicar por 10 la unidad de referencia, así que en un concierto machacón (unos 140Db y no nos estamos despeinando demasiado):
Tenemos 140Db 20 micropascales que son 110Db 20 milipascales, que son 80 DB 20 pascales, que son 50 DB 20.000 Pascales, que son 20 DB 20.000.000 Pascales, que son 2.000.000.000 Pascales.
O sea en un concierto nos estamos forrando bofetadas de 20.000 atmosferas de presión (ahí es na, dicho así parece mas ¿eh?)(la verdad es que ha salido tan alto que me sorprende hasta a mi, que alguien lo revise y me diga si no me he equivocado en algún punto, pero creo que no), en palabras de mi profesor (que me marcaron de por vida), “teneis suerte que la presión no os golpee en toda la supreficie corporal a la vez, por que sino en un concierto la gente estallaría como palomitas”.
El segundo dato que quería dejar (y también hablo de memoria) es que en acustica cuando un sonido se encuentra 3 DB por debajo de el ruido ambiente a su frecuencia se hace indistinguible, 3DB se corresponde con el doble de intensidad (más o menos) y para que la recepción sea buena se necesita que esté al menos 3 DB por encima del ruido ambiental (En ese momento es el ruido el que se enmascara).
Hasta aquí las curiosidades tontorronas del tito Ranta.
una vez mas gracias por el artículo!!! me ha encantao.
@Luis: Pues sí, quizá sea la edad. Pero 100 Hz es una frecuencia grave, pero no tanto como para que no la oiga el común de los mortales (que no tenga algún tipo de enfermedad, claro).
Para mí que ¡Van a ser los altavoces del PC!! La fidelidad media de los altavoces medios del PC medio suele ser bastante… digamos… escasa. Yo estoy por pensar que igual son ellos quienes tienen la culpa de que no la oigas.
La fidelidad media de los altavoces medios del PC medio suele ser bastante… digamos… escasa. Yo estoy por pensar que igual son ellos quienes tienen la culpa de que no la oigas.
Es verdad Mac. Creo que las especificaciones indicaban un rango de 200 a 16.000 Hz cuando lo compré, pero ya ni recuerdo el modelo concreto así que a lo mejor estoy diciendo una tontería monumental.
Eso me da esperanzas para mis oídos. No son ellos, son los auriculares
Los auriculares tienen muy poca definición en los graves (y esto se aplica incluso a auriculares con la palabra “studio” en sus especificaciones). Ésa es la razón por la que los técnicos de sonido nunca los usan para mezclar, masterizar, etc. Sólo los usan para monitorizar una grabación justo en el momemento de la interpretación, pero sus graves son tan imprecisos que puedes llegar a “ecualizar” el sonido con sólo moverlos en tus orejas… Sobre esto, seguro que puede aportar mucho más el amigo juanfilas.
Gracias por vuestros comentarios.
Llego cantando el Trololo Oh! un artículo nuevo! Vamos a trollear… Comienza a leer Pero… pero…. ni un fallo….. y lo entiendo todo! Esto no es posible!!!! Aaaaaaargh! [/randommode] Muy bueno y muy interesante, y justo sobre lo que he dado de acústica en música este año(que más se puéh esperar de 2º de la ESO?)
Es un artículo de una calidad brutal, y lo utilizaré el curso que viene (¡en 2º de ESO, Kratso!) cuando explique, una vez más, estas cosas. Extraordinario el trabajo de los tres (Compotrigo, J y Mac) para pulirlo y dejarlo como está. Ex-tra-or-di-na-rio
Illo, ta queao nike nike.
Gazapo de tipeo: “lo normal es que los altavoces no suenen igual el todas las frecuencias”
Lo único que he echado de menos es una breve nota sobre la relación del sonido con nuestro tímpano, nuestro detector de ondas (a no ser que eso se viera en el primer capítulo, que ya me podrías haber avisao antes, caraho , pero ya te digo, un trabajo fino, bien documentado, añadiendo experiencias personales que lo hacen cercano, con ejemplos sonoros a tutiplén, enlaces bien elegidos, diferenciando el lenguaje cotidiano del técnico/científico… Totá, que está mu bien.
, pero ya te digo, un trabajo fino, bien documentado, añadiendo experiencias personales que lo hacen cercano, con ejemplos sonoros a tutiplén, enlaces bien elegidos, diferenciando el lenguaje cotidiano del técnico/científico… Totá, que está mu bien.
Me voy a atacar la primera parte…
@Illo: Arreglao. No se pué consentir una errata en este peaso de artículo, quillo…
Y lo del oído humano, no lo busques en la primera parte; quizás debas esperarte a artículos sucesivos…
¡¡¡Excelente artículo!!! me has dado una mano enorme ya que esto ayuda muchísimo para que se entienda el próximo artículo mio que trata sobre distorsiones y como afectan cada una a la música en si.
Compotrigo: Los auriculares suelen ser lo mejor para escuchar música ya que su distorsión es bajísima y son muy planos a todas las frecuencias (incluso graves del orden de 20 a 25hz), es mas, en cualquier estudio de grabación ademas de unos buenos monitores por lo general hay dos o tres auriculares distintos ya que con estos escuchamos mucho mas detallada la grabación. El problema de escuchar con auriculares es que: 1° los sonidos graves ademas de escucharse se “sienten” en el cuerpo por la amplitud que suelen tener (mueven mucho aire) y en los auriculares solo los escuchamos, dando un resultado pobre en “sentimiento”. y 2do la imagen sonora es mas difícil de reproducir por auriculares, pero de esto ya hablaremos en el futuro .
.
pd: Para los que se quieran romper la cabeza un rato pensando, mezclen la serie “eso que llamamos tiempo” con esta y analicen el concepto de “timbre” y “música”, el mismo es un concepto subjetivo, una cualidad perceptual de nuestro cerebro, un instrumento o un altavoz no tiene “timbre” tiene una suma de ondas armónicas, la forma en que nuestro cerebro las mezcla y da el timbre, tiene que ver mucho de como sentimos el paso del tiempo, y eso a su vez influye en el concepto de “presente” ya que cuando escuchamos música parece como si la “duración” del presente fuese mas larga y componemos un pasaje musical como un solo ente entendible por nuestra consciencia… ¿para pensar un rato no?
¡Saludos!
juanfilas, entonces supongo que debo retractarme de lo que dije antes: “Los auriculares tienen muy poca definición en los graves (y esto se aplica incluso a auriculares con la palabra “studio” en sus especificaciones). Ésa es la razón por la que los técnicos de sonido nunca los usan para mezclar, masterizar, etc. Sólo los usan para monitorizar una grabación justo en el momemento de la interpretación, pero sus graves son tan imprecisos que puedes llegar a “ecualizar” el sonido con sólo moverlos en tus orejas…”
Lo cierto es que hablaba de memoria, eso lo leí hace años en una revista especializada, aunque siempre había entendido que los monitores de estudio de respuesta plana eran lo mejor para mezclar, mucho mejor que los auriculares… En fin, el tema de los altavoces se sale demasiado de mi campo de conocimientos. Espro desasnarme un poco más leyendo tu serie
Rantamplan, me alegra verte por estos lares. Si tú estudiaste lo de los decibelios en la uni, bien podría deleitarnos con un artículo más profundo al respecto, estoy seguro de que aquí siempre tendrás una buena acogida.
Por cierto, en el primer borrador de este artículo nombré los decibelios de pasada. Fue J quien me dijo que ya que se decía que la intensidad se medía en decibelios, en algún sitio se debía contar que se trataba de una unidad logarítmica.
Luego, tras documentar ese asunto un poco más, J volvió a aportar con lo del umbral de referencia, así que prácticamente todo lo referente a la medida de la intensidad se lo debéis a él.
Mi agradecimiento a J por sus aportaciones y a Mac por su interés, por permanecer en continua comunicación, por ayudar ecualizando las capturas de pantalla que le enviaba, por el vídeo, por las sugerencias y correcciones…
Me quedan una sensación de trabajo bien hecho y otra de formar parte de un equipo. No sé cuál de las dos es más chuli
Si, lo modificaría para que no se generen errores de interpretación, igualmente es una parte muy pequeña del articulo.
Saludos
A mí lo que más me cuesta imaginar son las ondas con distinta forma. Siempre me la imagino senoidal pero ¿Una onda triangular? ¿Cuadrada? ¿Existe tal cosa en la naturaleza o solo sabemos de ellas porque las creamos artificialmente? ¿Hay algún instrumento de cuerda, percusión, viento que emita ondas cuadradas, por ejemplo? ¿O se llegó a ellas solo por deducción de descomposición de ondas? Aún con la de diente de sierra me puedo imaginar una senoidal muy acuciante en sus crestas, pero ¿la cuadrada? ¿Se pueden crear formas de onda pentagonales, hexagonales o con la forma de las orejas de Mickey Mouse? (es decir, donde la cresta y el valle lleguen después que la “ladera”)
“¿Una onda triangular? ¿Cuadrada? ¿Existe tal cosa en la naturaleza o solo sabemos de ellas porque las creamos artificialmente?”
La verdad, no sabría decirlo.
“¿Se pueden crear formas de onda pentagonales, hexagonales o con la forma de las orejas de Mickey Mouse?”
Se puede crear cualquier forma de onda imaginable (con un ordenador, incluso puedes dibujarlas a placer) siempre que nunca haya más de un valor de y por cada valor de x (lo digo por las orejas de Mickey, sólo podrías dibujar medias orejas, una semicircunferencia). Fíjate que, en realidad, como lo que representamos de una onda es su amplitud (eje Y) en el tiempo (eje X), la forma de onda depende de la velocidad con la que varía la amplitud. Y, como creo que sé quién eres, Illo, me parece que tú eres capaz de imaginarte hasta la derivada de la amplitud con respecto al tiempo
Muy buen articulo, algo muy comun muy bien explicado. Ya eran cosas que sabia y me han quedado algunas dudas que palnteas. Las distintas frecuencias vienen como comentas de los modos propios de vibracion, de los que estamos mas acostumbrados a hablar de uno. En relaidad todos son recuencias de resonancia aunque por suerte al estar amortiguados no solemos explotar al pasar por nuestras frecuencias propias pero un ejemplo bueno de esto esta en los motores, diseñados para funcionar a cierta frecuencia normalmente vibran mucho cuando se encuentran al ralentin y cuando se les hace ir muy rapido vuelven ha hacerlo. Yo siempre me he imaginado como el motivo de que pase esto el hecho de que basicamente todas las particulas esten unidas por fuerzas que se comportan como un muelle, asi si numeramos nuestras particulas que digamos que son ocho, habra una frecuencia para cada conbinacion de ellas, muchas posibilidades pero no estrictamente infinitas. Bueno supongo que no es una gran explicacion.
Respecto a la densidad no creo que deba afectar mucho la temperatura debido a que el sonido es una diferencia de presion me imagino que el oido usara de referencia la que hay en la atmosfera, que seria lo que cambiaria con la temperatura. Claro que tambien cambia dependiendo del dia, segun tengamos mucha atmosfera encima o no, asi que no creo que tenga por que cambiar. La velocidad de propagacion del sonido si que variara, pero estamos tratando de ondas y de unas variaciones de presion producidas por otro elemento, por lo que si que puede que el sonido te llegue antes o despues, pero no creo que cambie en su forma.
Cuando copias lo de J: “Se demuestra matemáticamente que cualquier forma de onda puede descomponerse en la suma de varias ondas senoidales de distintas frecuencias. Cualquiera. Es lo que se denomina el espectro de la onda. En el caso general, ese espectro llega hasta frecuencias infinitas, pero habitualmente los componentes en frecuencias muy altas y muy bajas son despreciables, y como de todos modos no oímos fuera de una determinada banda de frecuencias…”
Se demuestra matematicamente que se puede descomponer en infinitas ondas, no en varias (de hecho en infinitas funciones que nos de la gana, no solo senosoidales). En terminos matematicos, despreciar las frecuencias bajas no es que sea muy correcto claro que bajas es un termino relativo, pero lo normal al descomponer es obtener primero las bajas y luego decidir donde te has aproximado suficiente con las altas. Las altas nos servirian para descomponer una onda cuadrada o cosas asi estrañas. Claro que en electricidad es comun usar tanto filtros pasa altos como pasa bajos, pero eso suele ser para poder localizar una frecuencia en concreto.
En una onda cuadrada tenemos más de un valor de Y por cada valor de X que hay en el valle.
¡Excelente artículo! Esta serie y la de juanfilas me encantan. Creo que llevan camino de convertirse en una de las más apreciadas por los lectores.
Steve Vai, (y muchos otros: Joe Satriani, Hendrix, Stevie Ray Vaughan, el recientemente fallecido Gary Moore, Chet Atkins, Jimmy Page, Robert Johnson…) es una de las principales razones por las que los que tocamos la guitarra (bueno, en mi caso sería mejor decir hacemos un poco de ruido con la guitarra) nos planteamos tirarla por la ventana y no volverla a coger nunca. He estado en un par de conciertos suyos y ver como sus dedos danzan por el mástil es increible. Y si para llegar tocar cómo el hay que practicar 14 horas al día y dormir con un la sonando… en fin, nos conformaremos con disfrutar de su música.
Si me permites el off-topic, veo que usas Audacity. Gran programa y buen ejemplo de lo que es capaz el software libre.
increible, y solo llevamos dos articulos! además de encantarme por lo que aprendo ,es un articulo cientifico con el lenguaje de los musicos,asique por fin sabre de que hablan los condenados cuando dicen cosas como sostener una nota, o meterle un armonico redondo…yuhuuu! Gracias mil!
Pues yo no estoy tan seguro de que no influya la velocidad del medio. Si la onda va más rápida (aunque sea cosa del medio por el que se propaga), pues sencillamente no será ya la misma onda, otra cosa será si es despreciable o no para lo que tengas entre manos.
@Illo Hola Illo! Si que existen tales cosas como onda cuadrada u onda triangular en la …”naturaleza” Recuerda que natural es todo lo que permitan las leyes fisicas,y segun aquel fisico,todo lo posible es obligatorio = ) Imagina una clasica fuente zen de las que llenan un cubilete de agua y cuando ha alcanzado cierto nivel vuelca. (CLOC) La cantidad de agua en el cubilete en el eje y y el tiempo en la x darian lugar a una onda triangular (esta en concreto se le llama de dientes de sierra) Por qué? Porque va llenandose “a velocidad constante” hasta que se vacía “de golpe” Y diras,pero esto no es una señal….bueno, si conseguimos que una pantalla pinte el nivel del agua en una pantalla pasa a serlo? =) Si quieres una analogía mas eléctrica imagina una corriente constante llenando un condensador,hasta que supera un cierto voltaje y se vacía de golpe. ¡Pongo a Hermes por testigo!¡Cuándo acabe exámenes escribo una serie sobre electrónica! = P
Illo, la onda cuadrada alterna su valor entre dos valores extremos sin pasar por los valores intermedios, así que no hay más de un valor de y por cada vaor de x.
Illo cuando miras los dibujos de las ondeas representan diferencia de presion respecto a tiempo, no posicion. La velocidad en el medio solo afactaria a cada uno de los puntos que se trasladan en el espacio y mientras que lo hagan todos a la misma velocidad no afecta y la forma de la onda es la misma. Si el objeto emisor se mueve si que se produce alteracion, el efecto doopler, pero en ese caso no se produce un cambio en la velocidad de propagacion de la onda, que es siempre la del medio. La diferencia solo podria ser si la presion de referencia de nuestro cuerpo fuera constante, pero me pareceria raro.
Compotrigo, la serie es de las mejores que he visto en el Cedazo (cuestión de gustos ya sabéis) y eso que las he laído casi todas.
La verdad es que acercar la “música” a la gente que no la ha estudiado es un trabajo muy complicado, y lo estás haciendo desde una postura muy muy acertada. Los que algo sabemos podemos apreciar el esfuerzo para simplificar las cosas al estilo El tamiz, mientras te metes hasta el cuello para definir bien los conceptos, que al final van a ser las herramientas que usaremos todos para comprender los entresijos de las composiciones y las estructuras musicales.
De momento te pongo un 10. Ya iremos bajando la nota si hiciera falta. Pero vamos, estos textos deberían ser obligatorios para algunos (como el guitarra y el cantante de mi grupo) que usan la música denostando el estudio de ella.
Para concluir: cualquiera que toque “de oído” porque le ha enseñado un amigo o alguien a tocar, debería leerte cuando termines la serie para comprender la cantidad de cosas que está dejando en el tintero y que puede ayudarle a ser todavía mucho mejor músico de lo que pudiera ser. Que hay mucho buen músico “de oído” por ahí y es una pena que no se muestren como lo grandes músicos que pueden llegar a ser.
Yo tengo poco oído, pero muchas ganas
Gracias por el esfuerzo!
Estructuración, concepto y ejemplos están definidos y de altura científica y pedagógica adecuada a diferentes niveles. Lo probaré con mis alumnos. Gracias.
Esta informacion me ha ayudado en mucho gracias
{ 1 } Trackback
[...] Para empezar, las características básicas del sonido son: altura, duración, intensidad y timbre. Con respecto a esta pieza, desde mi punto de vista la duración de los sonidos es larga. Los sonidos se quedan resonando un par de segundos. Un sonido corto (de escasa duración) se extenderá poco en el eje horizontal (tiempo), mientras que un sonido largo ocupará una mayor región de dicho eje. Una página que me ha resultado de interés a la hora de hacer este ejercicio es la siguiente: https://eltamiz.com/elcedazo/2011/05/26/eso-que-llamamos-musica-parametros-del-sonido/ [...]
Escribe un comentario