En el artículo anterior de esta anticuada (pero intensa) serie sobre Lógica de aplicación para la informática, para confeccionar la cual estoy usando los apuntes de la asignatura de “Metodología” de mi lejanísimo Segundo de Carrera, de Informática, del año académico 1973-74, impartida por el desgraciadamente fallecido profesor D. José Cuena Bartolomé, llegamos a definir el proceso de deducción lógica dentro del cálculo proposicional. Habíamos visto cómo usar la implicación lógica, el modus ponens y alguna cosilla más.
Como veréis, en esta serie no aparecen ni los silogismos ni, prácticamente, el “modus tollens”[1] ni todas esas cosas tan de buen ver en la Lógica filosófica tradicional, por no decir medieval, o escolástica, o aristotélica, o sanagustiniana, vaya Vd. a saber.
Pero es que en aquella asignatura de tan misterioso nombre, “Metodología”, de un par de horas semanales nada más, nos quedamos siempre “en el chasis”, en los fundamentos que nos permiten definir, con sólo pensar un poco, todos los demás modos de “modus”, etc. Todo está gobernado por el álgebra de Boole. Ah, si los afanosos silogistas medievales hubieran conocido el álgebra de Boole, las cosas hubieran sido mucho más sencillas… pero aún faltaban algunos siglos para que George Boole, que nació en 1815, definiera su famosa álgebra.
Y el método de exposición que siguió Pepe Cuena, como ya dije, era desde lo particular a lo general, definiendo bien los ladrillitos y luego construyendo con ellos cada vez edificios más y más altos y complejos…[2] Pues ya nos estamos aproximando a “lo general”…
Estamos ya a mediados, casi finales de abril, el curso se está acabando. Las clases finalizaban por entonces a mediados de mayo, para realizar los últimos parciales y dedicar casi todo junio a los finales, y luego septiembre a los exámenes de recuperación.[3] El curso se está acabando… y la serie con él. El último tema del curso, y el que cierra el círculo, tendrá que ver con el Cálculo de predicados. Cedamos un día más la palabra a Don José…
Cálculo de predicados, sí, pero… ¿qué es un predicado?
Pues un predicado es alguna cosa que se dice de algo, una cierta información que se da acerca de un término (en gramática o lingüística, diríamos del sujeto).
Supongamos la frase “Juan es fontanero”. Aquí el término es “Juan”, mientras que el predicado es “es fontanero”, que nos informa de que Juan tiene ciertas habilidades que le permiten, entre otras muchas cosas, arreglar un grifo que gotea.[4] En este caso se trata de un predicado “monádico”, puesto que se refiere a un solo término (Juan) y se representa por P(x), siendo la variable x cada término a los que se refiere el predicado, aquellos términos para los que el predicado P(x) es cierto. En este caso P sería “ser fontanero” y x se referiría a todos aquellos humanos para los que “ser fontanero” sería cierto, entre ellos Juan, claro está. Podríamos decir algo como “Ser fontanero(x)”, por ejemplo.
Ahora bien, los predicados que usamos en la vida corriente no son todos monádicos, ni mucho menos, sino que muchos se refieren a dos términos a los que ponen en relación, como en “Luis es amigo de Juan”, que expresaríamos P(x,y) (P sería aquí “ser amigo”, y x e y, dos personas que cumplen esa relación de amistad, como en “Ser amigo(Luis, Juan)”), o también tres términos, como en “Zaragoza está entre Madrid y Barcelona”, que denotaríamos P(x,y,z), o cuatro… y así sucesivamente. Serían predicados diádicos, triádicos, etc, respectivamente.
.
Vamos al lío.
Si tenemos un cierto Conjunto Universal (los españoles, los hispanoparlantes, la Humanidad en pleno, las plantas de mi jardín… lo que sea), podemos definir un cierto predicado que sea cierto para todos y cada uno de los componentes de dicho Conjunto Universal (como en “Todos los hombres son mortales”), o bien que sea cierto solamente para algunos de ellos (como en “Algunos hombres son fontaneros”), o, por fin, que no sea cierto para ninguno (por ejemplo, “Ninguna planta de mi jardín sabe hablar”).
Creo que os habéis dado cuenta de que ésta es la definición formal de un concepto que estaba apareciendo de rondón en artículos anteriores de la serie, sobre todo en el de la implicación lógica y en el anterior, el del proceso deductivo. Me refiero a la distinción entre los predicados Universales, que aplican a todos los elementos que componen un cierto Conjunto Universal, y los Particulares, que sólo aplican a algunos elementos de dicho Conjunto Universal y no a otros.
Todo lo que hemos visto hasta ahora, la escurridiza implicación y el proceso deductivo, se aplican a cualquier proposición, sea del tipo que sea. Tanto nos da que las proposiciones sean ciertas en todo el universo o sólo en el rellano de mi escalera: el método para tratarlas es idéntico.
Es ahora, mediante el Cálculo de Predicados, donde se introduce el concepto Universal/Particular y donde se hacen distinciones evidentes según que un predicado sea de un tipo o de otro. Ladrillito a ladrillito, la casa cada vez es más alta y resistente…
.
Bueno, pues para la definición formal de estos predicados, que se refieren a todo un conjunto o a sólo una parte, necesitamos algo más, algo que nos ayude a cuantificar cuántos elementos están afectados. Este algo más son los cuantificadores ( ), que junto con la negación (
), que junto con la negación ( ) permiten expresar todos estos tipos de predicados.
) permiten expresar todos estos tipos de predicados.
Estos cuantificadores se definen de la forma siguiente:
Todos los hombres son mortales:  (siendo H: “Los Hombres”, y P: “ser mortal”, y se lee: “Para todo x perteneciente a Los Hombres, x es mortal”).
(siendo H: “Los Hombres”, y P: “ser mortal”, y se lee: “Para todo x perteneciente a Los Hombres, x es mortal”).
Algunos hombres son fontaneros:  (siendo H: “Los Hombres”, y P: “ser fontanero”, y se lee: “Existe algún x perteneciente a Los Hombres, donde x es fontanero”).
(siendo H: “Los Hombres”, y P: “ser fontanero”, y se lee: “Existe algún x perteneciente a Los Hombres, donde x es fontanero”).
Ninguna planta de mi jardín sabe hablar:  (siendo J: “Las Plantas de mi Jardín”, y P: “saber hablar”, y se lee: “Para todo x perteneciente a Las Plantas de mi Jardín, x no sabe hablar”).[5]
(siendo J: “Las Plantas de mi Jardín”, y P: “saber hablar”, y se lee: “Para todo x perteneciente a Las Plantas de mi Jardín, x no sabe hablar”).[5]
.
Como veis, hasta aquí no es muy complicado… Veamos ahora cuáles son las propiedades de los dos cuantificadores, el universal (Para todo) y el existencial (Existe), y cómo podemos representarlos en nuestra vieja conocida forma, como variables booleanas extraídas directamente del Cálculo Proposicional. No nos acobardemos: veréis que, en realidad es todo muy sencillo e intuitivo…
 implica que
implica que 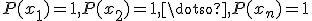 , es decir, todos y cada uno de los
, es decir, todos y cada uno de los  que forman el conjunto universal estudiado cumplen que
que forman el conjunto universal estudiado cumplen que 
En nuestro ejemplo de “todos los hombres son mortales”, esto quiere decir que Juan es mortal, Luis es mortal… etc, hasta El Tato es mortal: todos los individuos comprendidos en el conjunto de “Los Hombres” son mortales, por lo que “mortal(x)=1, para cualquier x”. Y esto lo podemos formular de forma sencilla como proposiciones, como vimos en el artículo correspondiente:
 o, en álgebra de Boole:
o, en álgebra de Boole:
 ,
,
Tranquilidad en la Sala… Esta formulita de nada no hace ni más ni menos que decir lo siguiente: si todo x perteneciente a X cumple P(x) implica que si tomamos por separado todos y cada uno de los “x” que integran el conjunto X, y miramos qué le pasa a P(x), entonces resulta que la proposición P(x) es cierta, o sea, 1, para todos los x. Si no fuera así, no sería “Para todo…”.
Por tanto, la conjunción (·) de todos los P(x) individuales es 1 también (puesto que 1·1·1…·1=1, evidentemente).
.
Por otra parte,  implica que habrá algún
implica que habrá algún  , al menos 1, en que ocurrirá que
, al menos 1, en que ocurrirá que  . Por ejemplo, como Juan es fontanero,
. Por ejemplo, como Juan es fontanero,  (siendo P “ser fontanero”, en este caso). En notación proposicional, esto quedaría:
(siendo P “ser fontanero”, en este caso). En notación proposicional, esto quedaría:
 o, en álgebra de Boole:
o, en álgebra de Boole:
 .
.
Ahora, lo que decimos con Existe un x perteneciente a X que cumple P(x) es, ni más ni menos, que al menos uno de todos los x que pertenecen al conjunto X debe cumplir que P(x)=1. Por tanto, la disyunción (la suma lógica, el +) de todos los P(x) tendrá como resultado 1, dado que hay uno, al menos un P(x), ése que “existe“, cuyo valor es 1. Entonces, por mucho que todos los demás P(x) valgan 0 (sean falsos), ese único valor verdadero (ese único Juan que sí que es un fontanero de rompe y rasga) hará verdadera la suma lógica.
.
¿Y qué pasa con la negación de un cuantificador? Veamos:
![\neg \forall x P(x) \equiv \neg [P(x_{1}) \wedge P(x_{2}) \wedge \dotso \wedge P(x_{n})] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_26ac8f372b0a19e14754fe82f2b427d4.png)
 , debido a la aplicación de la siempre tan útil Ley de De Morgan, y por tanto:
, debido a la aplicación de la siempre tan útil Ley de De Morgan, y por tanto:

Es natural y lógico. Decir que “No todo x cumple P(x)” es lo mismo que decir que “Existe un x tal que no se cumple P(x)“, o lo que es lo mismo, “Existe un x para el que no se cumple P(x)“, y por fin, “Existe un x tal que P(x)=0“.
O sea, traduciendo al lenguaje natural, si no todo el mundo es fontanero, es porque hay alguien, al menos uno, yo mismo sin ir más lejos, que no es fontanero. Una perogrullada como una casa.
¿Veis cómo en realidad las fórmulas son muy sencillas? Imponen, con tanta x y tanto simbolito raro, pero son evidentes.
Al contrario, es fácil demostrar que 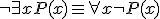 . Es decir, si no existe nadie que sea fontanero es porque todo el mundo no es fontanero. Otra vez evidente, al traducirlo al lenguaje cotidiano.
. Es decir, si no existe nadie que sea fontanero es porque todo el mundo no es fontanero. Otra vez evidente, al traducirlo al lenguaje cotidiano.
.
Entonces,  refiriéndose al producto lógico, o sea, booleano, y no a la multiplicación “normal”, como supongo que os habréis dado cuenta, y en cuanto al cuantificador existencial:
refiriéndose al producto lógico, o sea, booleano, y no a la multiplicación “normal”, como supongo que os habréis dado cuenta, y en cuanto al cuantificador existencial:
 [6]
[6]
.
Por otra parte, ¿qué pasaría si nuestro predicado no fuera monádico, sino que se refiriera a dos términos a los que pone en relación?
Pues, si tenemos la expresión  , podemos operar con ella de la siguiente manera:
, podemos operar con ella de la siguiente manera:
![\forall x \forall y f(x,y) = \forall x [\forall y f(x,y)] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_a8f45fce7aa4f2eb50cbb9cbd19d9cf1.png)
![\forall x [f(x,y_{1}) \wedge f(x,y_{2}) \wedge \dotso \wedge f(x,y_{n})] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_a8f6dc68bc18b9a180e0825e57a7c7ac.png)
![[f(x_{1},y_{1}) \wedge f(x_{1},y_{2}) \wedge \dotso \wedge f(x_{1},y_{n})] \wedge](https://eltamiz.com/elcedazo/wp-content/cache/tex_8b726b030c6a663899d218f9592128ba.png)
![[f(x_{2},y_{1}) \wedge f(x_{2},y_{2}) \wedge \dotso \wedge f(x_{2},y_{n})] \wedge](https://eltamiz.com/elcedazo/wp-content/cache/tex_f19eaeb7ddde06949317d6df94a8c63d.png) …
…
![\wedge [f(x_{n},y_{1}) \wedge f(x_{n},y_{2}) \wedge \dotso \wedge f(x_{n},y_{n}]) =](https://eltamiz.com/elcedazo/wp-content/cache/tex_b3ed7db8b2b201414fe979d1e7979cce.png)
 .
.
Este tocho de fórmulas es intimidante, de acuerdo, pero en lenguaje cotidiano es una obviedad. En realidad no quiere decir ni más ni menos que lo siguiente: que todas las posibles combinaciones de P(x,y), tomemos como tomemos los x’s y lo y’s, los emparejemos como los emparejemos, tendrán siempre como resultado 1, y por tanto, la conjunción (con Y, con ·) de todas ellas, como todas valen 1, será 1 también.
Así, por ejemplo, si decimos que en un pueblo todo el mundo es amigo de todo el mundo, con lo que el predicado básico es Ser Amigo(x,y), que valora si x e y son amigos (y valdrá 1 si sí que son amigos, y 0 si no lo son),[7] entonces, elijamos como elijamos las x’s y las y’s, sean quienes sean esos x e y, aunque vivan en los extremos más alejados del pueblo, son efectivamente amigos, así que para ellos el predicado Ser Amigo(x,y) es igual a 1, y por tanto la conjunción (el producto lógico) de todos ellos será 1 también. No es tan difícil, como veis.
Para tres variables (x,y,z), cuatro, etc, procederíamos de igual manera, generalizando esta misma fórmula.
Y naturalmente, dada la simetría del álgebra de Boole, podemos de la misma forma asegurar que 
No lo voy a escribir, pero cambiando el + y el · sale del tirón…
.
Por otra parte, es sencillo demostrar que los cuantificadores pueden “saltar” por los signos de conjunción o disyunción a través de las funciones. Veamos (y que no os intimiden las fórmulas, que parecen muy complicadas pero no lo son en absoluto).
En primer lugar, supongamos que tenemos los dos siguientes predicados individuales:
 : “Hace frío”, y
: “Hace frío”, y
 : “Todas las vacas tienen cuernos”, o, mejor expresado, “Para todo x perteneciente al conjunto de las vacas, x tiene cuernos”.
: “Todas las vacas tienen cuernos”, o, mejor expresado, “Para todo x perteneciente al conjunto de las vacas, x tiene cuernos”.
Entonces el predicado  significaría “Hace frío y todas las vacas tienen cuernos”. Es evidente que “p” es aquí un predicado que no tiene nada que ver con la variable y, es independiente a ella (porque hace frío, o no, independientemente de que las vacas tengan o no cuernos).
significaría “Hace frío y todas las vacas tienen cuernos”. Es evidente que “p” es aquí un predicado que no tiene nada que ver con la variable y, es independiente a ella (porque hace frío, o no, independientemente de que las vacas tengan o no cuernos).
Operemos ahora un poco con este predicado compuesto:
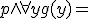
![p \wedge [g(y_{1}) \wedge g(y_{2}) \wedge . . . \wedge g(y_{n}) ] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_3ebc22701bae73f84766a672b4ecac79.png)
![[p \wedge [g(y_{1})] \wedge [p \wedge [g(y_{2})] \wedge . . . \wedge [p \wedge [g(y_{n})] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_44d08dddc1ec11b375f4cecbd3dbd3be.png)
![\forall y [p \wedge g(y)]](https://eltamiz.com/elcedazo/wp-content/cache/tex_eddd500caaf66d9bcd433e967139f4ed.png)
Es decir: ![p \wedge \forall y g(y) = \forall y [p \wedge g(y)]](https://eltamiz.com/elcedazo/wp-content/cache/tex_71790d49b101292787ca471c23697a30.png) , lo que quiere decir en nuestro ejemplo que “Para todo x perteneciente al conjunto de las vacas, hace frío y x tiene cuernos”. Como veréis es incluso realmente difícil expresar esta sutil distinción en español.
, lo que quiere decir en nuestro ejemplo que “Para todo x perteneciente al conjunto de las vacas, hace frío y x tiene cuernos”. Como veréis es incluso realmente difícil expresar esta sutil distinción en español.
Ahora veamos qué le ocurre al siguiente predicado:  . Operando:
. Operando:

![[f(x_{1}) \wedge . . . \wedge f(x_{n})] \wedge [g(y_{1}) \wedge . . . \wedge g(y_{n})] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_42e0203f2b0af6c2ade888fae361c326.png)
![[f(x_{1}) \wedge (g(y_{1}) \wedge . . . \wedge g(y_{n}))] \wedge](https://eltamiz.com/elcedazo/wp-content/cache/tex_016735967c5ca240b1107149e740daa1.png)
![[f(x_{2}) \wedge (g(y_{1}) \wedge . . . \wedge g(y_{n}))] \wedge](https://eltamiz.com/elcedazo/wp-content/cache/tex_fa1319fd101d0181405dcab0d1bd799e.png)
. . .
![[f(x_{n}) \wedge (g(y_{1}) \wedge . . . \wedge g(y_{n}))] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_06a9893234bc9aa8d8f461914c9dc084.png)
![[f(x_{1}) \wedge \forall y g(y)] \wedge [f(x_{2}) \wedge \forall y g(y)] \wedge . . . [f(x_{n}) \wedge \forall y g(y)]](https://eltamiz.com/elcedazo/wp-content/cache/tex_89fde76a549afb85ed8a989d761648ab.png)
Aquí, cada predicado  es independiente de
es independiente de  (tiene que ver con la variable x, que es obviamente distinta de y), así que podemos aplicar la propiedad que demostramos unas líneas más arriba. Queda que:
(tiene que ver con la variable x, que es obviamente distinta de y), así que podemos aplicar la propiedad que demostramos unas líneas más arriba. Queda que:
![[f(x_{1}) \wedge \forall y g(y)] \wedge [f(x_{2}) \wedge \forall y g(y)] \wedge . . . [f(x_{n}) \wedge \forall y g(y)] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_b73af716f28174d197d2fccbee71392d.png)
![\forall y [f(x_{1}) \wedge g(y)] \wedge \forall y [f(x_{2}) \wedge g(y)] \wedge . . . \wedge \forall y [f(x_{n}) \wedge g(y)] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_ecb2cc554a3fb14cd7699340ed39b461.png)
![\forall x [\forall y (f(x) \wedge g(y))] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_130b0c6aefdddcefe1cae7df5531a2cc.png)
![\forall x \forall y [f(x) \wedge g(y)]](https://eltamiz.com/elcedazo/wp-content/cache/tex_a9e59e12537cb59ea922b0bda0b06429.png)
Entonces podemos finalmente afirmar que:
![\forall x f(x) \wedge \forall y g(y) = \forall x \forall y [f(x) \wedge g(y)]](https://eltamiz.com/elcedazo/wp-content/cache/tex_74cdf1b52eeda0448391a237494a1276.png) , y que el cuantificador “Para todo” puede saltar a través de la fórmula del predicado, a guisa de saltimbanqui…
, y que el cuantificador “Para todo” puede saltar a través de la fórmula del predicado, a guisa de saltimbanqui…
Análogamente (esto ya no lo demuestro: es prácticamente inmediato en base a lo anterior):
![\exists x f(x) \wedge \exists y g(y) = \exists x \exists y [f(x) \wedge g(y)]](https://eltamiz.com/elcedazo/wp-content/cache/tex_ef70b1510edd20e4878969bc62cc35b4.png) y por fin:
y por fin:
![\forall x f(x) \wedge \exists y g(y) = \forall x \exists y [f(x) \wedge g(y)]](https://eltamiz.com/elcedazo/wp-content/cache/tex_191308724d4c1cd5088f99bd0b786a8a.png) Bello, ¿no?
Bello, ¿no?
.
Se define entonces la Forma Normal PRENEX para representar fórmulas en Cálculo de Predicados, donde las funciones adoptan la forma siguiente:
Primero, todos los cuantificadores, en cabeza de la fórmula, aprovechando que pueden “saltar” a través de ellas.
Después, todas las expresiones, ligadas exclusivamente por conjunciones,  , o disyunciones,
, o disyunciones,  , y donde la negación, las que haya, están aplicadas exclusivamente a las proposiciones simples, no a expresiones.
, y donde la negación, las que haya, están aplicadas exclusivamente a las proposiciones simples, no a expresiones.
Esta última parte es sencilla de ver, pues ya vimos cómo se podía convertir cualquier expresión booleana a una suma de productos, para llegar a expresar toda función booleana en su Forma Normal Disyuntiva (o Conjuntiva, tanto da)… y dado que los cuantificadores pueden “saltar” a través de la expresión (siempre que se refieran a las propias variables sobre las que saltan, o bien sean independientes de ellas), no es muy difícil llegar a escribir cualquier predicado, por compleja que sea su expresión, en Forma Norma PRENEX. Con ello se consigue tener una forma de expresión que permite comparar diferentes expresiones con predicados, para ver si son iguales o, si no lo son, en qué se diferencian (algo similar a lo que se obtenía mediante la Forma Normal Disyuntiva, si os acordáis).
.
Un ejemplo. Se pide escribir en Forma Normal PRENEX la siguiente expresión:
![\neg \exists x [p(x) \Longrightarrow \forall y q(y)] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_21d6264daaa7faafc71c30c9de3ced02.png)
Veamos…
![\neg \exists x [p(x) \Longrightarrow \forall y q(y)] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_21d6264daaa7faafc71c30c9de3ced02.png) en primer lugar, una simplificación de la implicación “
en primer lugar, una simplificación de la implicación “ ” …
” …
![\neg \exists x [\neg p(x) \vee \forall y q(y)] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_8336c921404dad2e04893625a582477c.png) ahora un cambio de cuantificador negado: No existe ningún x tal que R(x) es lo mismo que Para Todo x se cumple que No R(x). R(x) aquí hace referencia a la expresión compleja que hay dentro del paréntesis…
ahora un cambio de cuantificador negado: No existe ningún x tal que R(x) es lo mismo que Para Todo x se cumple que No R(x). R(x) aquí hace referencia a la expresión compleja que hay dentro del paréntesis…
![\forall x \neg [ \neg p(x) \vee \forall y q(y)] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_3255afd7db3495b886be2e61a84407a3.png) la negación entra dentro del paréntesis, y en el camino cambia el
la negación entra dentro del paréntesis, y en el camino cambia el  por el
por el  , según la Ley de De Morgan…
, según la Ley de De Morgan…
![\forall x [p(x) \wedge \neg \forall y q(y)] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_cffea7181ea4bd863b69a4e316ee5f8c.png) otro nuevo cambio de cuantificador negado: No todo y cumple Q(y) es lo mismo que Existe un y tal que No se cumple Q(y)…
otro nuevo cambio de cuantificador negado: No todo y cumple Q(y) es lo mismo que Existe un y tal que No se cumple Q(y)…
![\forall x [p(x) \wedge \exists y \neg q(y)] =](https://eltamiz.com/elcedazo/wp-content/cache/tex_e53596a84e44152fbfb5ca9e4f21c54b.png) ahora el cuantificador existencial salta, a modo de saltimbanqui, a través del paréntesis…
ahora el cuantificador existencial salta, a modo de saltimbanqui, a través del paréntesis…
![\forall x \exists y [p(x) \wedge \neg q(y)]](https://eltamiz.com/elcedazo/wp-content/cache/tex_48048f4e77f64473698c240d12e415f5.png) , et voilà!, la expresión resultante ya está en Forma Normal PRENEX.
, et voilà!, la expresión resultante ya está en Forma Normal PRENEX.
.
Vaya. Ha salido un artículo relativamente cortito para mis costumbres. Pero otra vez intenso. Creo.
Se está terminando el mes de abril… de 1974. Sólo quedan un par de clases, como mucho,[8] antes de los exámenes finales, así que usamos esas dos clases finales para terminar con algún detalle y hacer ejercicios para ejercitarnos antes de dichos exámenes… pero aún da para otro artículo más, que, esta vez sí, será el último de esta serie sobre Eso que llamamos Lógica que rememora las clases que Don José Cuena impartió a los alumnos de Segundo de Informática aquel calentito año de 1974… Hasta entonces.
Disfrutad de la vida, mientras podáis.
- Ni mucho menos el “modus ponendo tollens”, el “modus tollendo ponens” ni ningún otro tipo de inferencia clásica… sabiendo álgebra de Boole y cálculo proposicional, no hacen falta. [↩]
- Es lo que los consultores llamarían un método “bottom-up”, o de abajo arriba, en contraposición al método “top-down”, de arriba abajo, o desde lo general a lo particular. [↩]
- Ahora, con eso de “Bolonia”, el calendario universitario tradicional ha cambiado tanto que ya no sé cómo funciona. [↩]
- Atentos al dato: Lo que yo tengo anotado en mis apuntes, el ejemplo que usó Pepe Cuena en 1974, no era “Juan es fontanero”, no, sino que era… “Juan es negro”. En aquella época, decir de alguien que “era negro” no tenía ninguna acepción extraña: su piel era de color negro o de algún tono más o menos chocolate, y punto. Si ahora se me ocurre poner en el texto principal, “Juan es negro”, así por las buenas, sirviéndome además para casi todos los ejemplos y diatribas posteriores, seguro que me cae la del pulpo. Ay, ¡cómo ha cambiado la sociedad española en cuarenta años! ¡Y qué mal llevo yo lo de la “corrección política”, eso de “personas de color”, “ciudadanos y ciudadanas”, “miembros y miembras” y demás sandeces, memeces y estupideces por el estilo. [↩]
- Al menos, no saben hablar en español… [↩]
- No tendré que repetir aquí que se trata de una suma lógica, y no aritmética… ¿verdad? [↩]
- Y no, no vale “0,5″ si son conocidos pero no se llevan muy bien y tal… sólo 0 y 1. [↩]
- Y eso si no hacemos huelga por alguna importante razón; a mediados de los setenta del siglo pasado ésa era una situación bastante común… los únicos que podían hacer huelga sin terminar en el trullo éramos los estudiantes, aunque ciertamente la autoridad de entonces lo llamaba más bien “hacer pellas”. [↩]

The Eso que llamamos Lógica (VIII) El cálculo de predicados. by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.





{ 15 } Comentarios
Creo que hay una cosa que está incompleta. Cuando explicas el cuantificador exitencial, pones que debe cumplir la condición de que el sumatorio de todos los P(xi) debe ser uno, pero eso también lo cumple el cuantificador universal, no es concluyente. Es sólo condición necesaria, pero no suficiente. Para que se pueda definir así, debería añadirse otra condición más, como por ejemplo que el producotrio (o como se diga), sea 0, o bien, que algún P(xi) sea cero (aunque creo que esta última, podría meter la revisión en cierta recursividad).
Creo que como explicación sí se ve claramente lo que quieres decir, pero como definición, está un poco coja.
Por lo demás, a ver si me leo con más calma lo de los predicados con más de dos términos, que con tanta fórmula, si no lo leo atentamente, me lío bastante.
Te equivocas, Battosay. La disyunción es siempre tratada como inclusiva (sólo cuando resulta exclusica se remarca que es exclusiva y en este caso su simbolo es una uve subrayada).
No es necesario que algún P(xi) sea cero, pueden ser tranquilamente todos unos precisamente porque la disyunción inclusiva lo permite.
La definición es perfecta tal y como está escrita. Si acaso, justificar porqué es la que es, y no la que tú crees que es.
No entiendo qué tiene que ver que la o sea inclusiva o exclusiva, sé que se refiere a la inclusiva. Permíteme un ejemplo. Tenemos un P que es “es hombre” y un universo de Macluskey y yo (que soy hombre).
P(Macluskey) = 1 P(Battosay) = 1
Entonces, comprobamos el operador universal:
P(Macluskey) AND P(Battosay) = 1 AND 1 = 1
Probamos con el existencial:
P(Macluskey) OR P(Battosay) = 1 OR 1 = 1
Si definimos el existencial y el universal como incluyentes, pues me vale la definición. Pero si son excluyentes, la definición de Mac no me vale. No sé si me explico.
@Battosay: Creo que lo que te pasa es que no estás teniendo en cuenta que en realidad el cuantificador universal no representa ni más ni menos que un caso especial del existencial…
Vale. Me explico:
Si miras la tabla de verdad de la conjunción (AND, para entendernos) y de la disyunción (OR) verás que hay un caso particular en que ambos son ciertos: cuando ambas proposiciones individuales son ciertas.
Es decir, si se cumple que A AND B es cierto, también lo es obligatoriamente A OR B… ¿no? Y sin embargo es claro que el AND y el OR son distintos…
Aquí es igual, exactamente igual. Supongamos que decimos que “Para todo x perteneciente a los habitantes de un cierto pueblo, x es rubio”. En este caso… ¡también es perfectamente cierto que “Existe algún x de ese pueblo tal que x es rubio”! ¡Todos, de hecho, lo son!, luego “al menos uno lo es”… ¿De acuerdo?
Pero, en cambio, si tenemos que “Existe algún x tal que x es rubio”, no podemos afirmar lo siguiente: “Para todo x, x es rubio”, ni mucho menos, pues de la primera podemos inferir que podría haber algún habitante del pueblo que fuera moreno o pelirrojo, y seguiría siendo válida… de hecho, bastaría con un solo habitante del pueblo que fuera rubio para hacer cierta la sentencia con el cuantificador existencial…
En una palabra, como te comentaba Ammonio, la definición del texto es correcta, es decir, es necesaria y suficiente, pues no se necesita más para definir el “Existe”. Lo sé porque la he copiado esmeradamente de mis procelosos apuntes…
Piénsalo un momento, ponte un ejemplo, y seguro que lo ves claro.
Gracias por vuestros comentarios.
Saludos
Pero es que estamos ante una disyunción inclusiva (OR), no ante una disyunción exclusiva (EOR). Por eso la deficición está bien sin incluir la excepción de dices.
El sumatorio será 1 en todos y cada uno de los siguientes casos.
-P(Macluskey) OR P(Battosay) = 1 OR 1 = 1;
-P(Macluskey) OR P(Battman) = 1 OR 0 = 1
-P(Mikemouse) OR P(Battosay) = 0 OR 1 = 1
Si estuviésemos ante un EOR el primer caso resultaría cero y verdadero sólo en los dos siguientes.
No sé si me explico bien.
Con otras palabras:
Si se admite la exepción que propones (al menos uno de ellos ha de ser falso) la tabla de verdad de la suma lógica que compone el cuantificador existencial quedaría como sigue:
-P(Macluskey) OR P(Battosay) = 1 OR 1 = 0; -P(Macluskey) OR P(Battosay) = 1 OR 0 = 1; -P(Macluskey) OR P(Battosay) = 0 OR 1 = 1; -P(Macluskey) OR P(Battosay) = 0 OR 0 = 0;
Justamente ésta es la tabla de verdad de la disyunción exclusiva (que casualmente es la negación del bicondicional lógico o “coimplicación”).
Precisamente porque puede darse el caso de que todos los miembros de una disyunción inclusiva son verdaderos (ver mi intervención anterior) no podemos decir que que algún P(xi) sea cero.
Matizo: que algún P(xi) tenga que ser necesariamente cero
@ Macluskey, vale, si tomamos que el universal no representa más que un caso del existencial, aceptamos barco. Lo que pasa es que no me acaba de cuadrar, es más una forma de como veo yo las cosas que de como son en realidad. Para mí, decir “existe al menos algún” o “existe algún”, me sugiere que hay algunos que sí y otros que no, cuando, realmente, puede ser que existan todos. Quizás sea más un problema de semántica que matemático.
Por otro lado, volviendo a leer el artículo, creo que también puede ser por definir primero el universal y luego el existencial. Al ir del caso particular al general, busco, inconscientemente, alguna forma de diferenciarlos sí o sí. Mientras que si fuera al revés algo así como, “si se dan estas condiciones existe alguno, pero es que si, además, se da esta, existen todos”.
Vamos que comprendido, pero por mi forma de ver las cosas, un poquillo a regañadientes.
@Amnonio, insisto en que la OR exclusiva e inclusiva no tiene nada que ver con mi duda, te estás centrando en un caso particular, que es el de dos variables, te voy a poner un ejemplo con tres. Sigamos mi razonamiento en el caso de ampliar a tres el universo, Mac, la hija de Mac y yo.
P(Mac)=1 P(HijaMac)=0 P(Battosay)=1
Según mi razomaniento anterior:
P(Mac) OR P(HijaMac) OR P(Battosay) = 1 OR 0 OR 1 = 1 P(Mac) AND P(HijaMac) AND P(Battosay) = 1 AND 0 AND 1 = 0
Me sale existencial. Pero si hago como tú dices que hago, aplicar el or exclusivo:
P(Mac) XOR P(HijaMac) XOR P(Battosay) = 1 XOR 0 XOR 1 = 0
Es que me sale que no existe ninguno, cuando tenemos dos que existen. Y, de todas formas, te lo digo yo, que mi problema no es que confunda XOR con la OR, que no la confundo, que es otra cosa, lo que le he dicho a Mac arriba.
Y otra cosa, si el P que estamos usando es el predicado “es hombre”, ¿cómo es que “P(Macluskey) OR P(Battman) = 1 OR 0 = 1″? ¿Insinúas que Batman no es un hombre? ¿Qué quieres decir con eso? ¿Acaso dudas de su virilidad? A ver si vamos a tener un problema.
@Battosay: Si para ti, de “existe al menos uno que cumple tal cosa” deduces que “tiene que existir al menos uno que no cumple tal cosa”… pues vale; es lo que tiene el lenguaje: los aspectos semánticos son tan ricos (y tan complicados) que hacen difícil (¡y divertido!) comunicarse.
Pero ahora veámoslo con orientación “científica”.
Vas de viaje a un territorio desconocido y te encuentras con un nativo (el único que has visto hasta ahora) que tiene el pelo verde. Y anotas en tu libreta de expedicionario: “Existe al menos un nativo tiene el pelo verde”.
Sigues caminando y te encuentras con más nativos, todos con el pelo verde… pero de momento no puedes modificar tu observación, que es: “Existe al menos un nativo tiene el pelo verde”.
No puedes decir “TODOS los nativos tienen el pelo verde” porque no has visto a todos y cada uno de los nativos, por lo que no puedes afirmar la Universalidad de la verdez en la cabellera de los nativos.
Pero, por la misma razón, tampoco puedes pensar que haya obligatoriamente algún nativo con el pelo rojo, o morado o qué sé yo. No mientras no descubras uno. Si lo haces, debajo de “Existe al menos un nativo tiene el pelo verde” escribirás que “Existe al menos un nativo tiene el pelo morado”, por ejemplo, y santas y buenas.
Y si efectivamente has conseguido ver a todos y cada uno de los nativos y todos tienen el pelo verde, sólo entonces podrás asegurar que “TODOS los nativos tienen el pelo verde”… pero eso no invalida la primera anotación, ésa de “Existe al menos un nativo tiene el pelo verde”, que sigue siendo rigurosamente cierta.
Bueno, espero que este verdoso comentario te ayude a entender la diferencia…
Saludos
Ah, el copy-paste…
Naturalmente no es “Existe al menos un nativo tiene el pelo verde” , sino:
“Existe al menos un nativo QUE tiene el pelo verde”. Lo pones mal la primera vez y luego lo pegas doce veces.. y todas mal.
En fin.
Je, je. A Batman lo supongo un ente de ficción, por tanto inexistente.
A lo serio: la mejor manera de leer una disyunción inclusiva es “existe al menos algún x” lo cual quiere decir que por lo menos uno necesariamente tiene que existir para que sea válida la disyunción, lo cual quiere decir que también sería válida si existen dos, tres, incluso si existen todos.
Otras dos cosas:
¿Qué significa “me sale existencial”? Lo único que te sale es que no están todos y cada uno de los miembros de la conjunción lógica.
-”Pero si hago como tú dices que hago, aplicar el or exclusivo: P(Mac) XOR P(HijaMac) XOR P(Battosay) = 1 XOR = 0 Es que me sale que no existe ninguno, cuando tenemos dos que existen”.
¿De dónde sacas que no existe ninguno? lo único que estás expresando es que (recuerda que es la negación del bicondicional) no se da el caso de que la verdad del primero suponga la falsedad del segundo (en este caso 0 XOR 1) y que de la verdad del segundo no se sigue la falsedad del primero. La lectura que haces es muy rara, ten en cuenta que el resultado es el valor del funtor, no el valor existencial de los individuos.
Voy a dejarlo ya porque me da la sensación de que lío más a la gente de lo que puedo ayudarla.
@Mac, veo la diferencia, lo que pasa es que, quizás acostumbrado a ver esta terminología en teoremas y explicaciones matemáticas, uno se condiciona un poco. Suele ser algo tal como “para todo x (universal), existen un y (existencial)”. El poso que me deja a mí es que el existencial es algo como “a veces sí y a veces no”, vamos que siempre hay alguno que no, por eso veía coja la definición. Pero si el existencial incluye el universal, perfecto. Como ya dije arriba, creo que si los hubieras puesto al revés, muy posiblemente, ni me hubiera surgido tal duda.
En cuanto a tu ejemplo, lo veo perfectamente. Quizás dandole otra vuelta, se vea mejor mi problema. Supongamos que yo consigo hacer un censo de todos los indígenas estos y tienen todos el pelo verde. Publico mi investigación y después salen el los periódicos estos titulares:
Periódico I: “Existe un indígena con el pelo verde”. Periódico II: “Todos los indígenas tienen el pelo verde”.
¿A que todos diríamos que el primero es parcial? Sin embargo no ha mentido. Por eso me cruje a mí un poco. Que sí, que vale, que el operador existencial engloba al universal, pero. coño, que si es universal y decimos que el global, como que a mí me suena incorrecto. Sé que matemáticamente (o logicamente en este caso) es correcto, pero queda, por lo menos para mí, incompleto.
Por eso me cuesta tanto, si es para todos, pues es para todos, ¿por qué decir que simplemente hay algunos?
@ Ammonio, vaya se superpusieron los comentarios. Te explico lo que quiere decir. Yo tengo un predicado “es hombre” y un universo”Mac, su hija y yo”, y quiero saber si ese predicado es existencial o universal en mi universo. Saco los valores del predicado para cada valor del universo y aplico las definiciones de universal y existencial a ver qué me sale.
Como tú me estabas diciendo que estoy confundiendo, en la definición de existencia,l el OR con el XOR, te quería demostrar que ese no era mi problema, poniéndote un caso con tres variables donde se ve claramente que mi confusión no tiene nada que ver con la OR y la XOR, si no con una restricción a mayores que yo quería añadir, por que yo lo valgo, a la definición.
Ok, ahora veo tu duda.
Piensa en el siguiente expresión: “para todo x (único en su clase y por tanto universal) existe un y (existencial) tal que …”. En este caso no ocurre eso de unas veces sí y otras veces no. No ocurre ningún caso en el que no.
Ejemplo: Para todo Battosay existe una camisa (que puede ser desde una única camisa, hasta todo el conjunto de camisas que se hayan fabricado a lo largo de la historia) tal que Battosay es dueño de una camisa (o inluso podría ser que de todas).
A mí me dió clase D. José Cuena en la Facultad de Informática, en los años 83-84. Era uno de los mejores profesores que he tenido. No sabía que hubiera muerto.
Escribe un comentario