Esta serie se denomina “Eso que llamamos Lógica”, creo que os habréis dado cuenta. Presuntuoso nombre, seguramente. Sin embargo, el caso es que hasta ahora poco hemos visto de Lógica-Lógica, no sé si me explico…

Sirva en mi descargo que nos hemos estado preparando para ello, pues hasta ahora hemos visto cómo es el álgebra de Boole con su Forma Normal Disyuntiva, luego entramos en la base del álgebra de Circuitos, y por fin, en el artículo anterior vimos el álgebra de Conjuntos desde la óptica del álgebra de Boole… pero ya con una cierta aplicación a la resolución de problemas lógicos, lo que muchos de vosotros llamaríais “Acertijos”, como el ínclito e incombustible “¿Cómo se llama el maquinista?”, que os dejé de regalo en el capítulo anterior de la serie. Espero que su resolución no os haya destruido muchas neuronas.

Como sabéis, porque lo he dicho en cada capítulo, en realidad estoy siguiendo mis emborronados apuntes de la asignatura de “Metodología” de Segundo de Informática, curso 1973-74, impartido por José Cuena Bartolomé, desgraciadamente fallecido en 1999, uno de los mejores profesores que he tenido en mi vida.

Supongo que os habréis dado cuenta del método didáctico seguido por Pepe Cuena para desasnarnos en estas lides…

Empezó por la base teórica, el álgebra de Boole, luego nos explicó aplicaciones de la misma a problemas distintos (los circuitos eléctricos, los conjuntos), para llegar al cálculo proposicional… Iba paulatinamente definiendo los ladrillitos con los que se construirían los edificios cada vez más altos de la Lógica. No daba nada por sentado, sino que definía las cosas de lo particular a lo general…

Al final del artículo incluiré unos párrafos explicando todo esto de forma más detallada, para que no os perdáis en lo que sigue. Leedlo y podréis seguir lo que queda de serie con facilidad… espero.

.

En fin, a estas alturas del curso (debía ser enero o febrero de 1974), Don José nos dijo que ya estaba bien de holgazanear, que ya iba siendo hora de entrar en materia, lógicamente, con la Lógica de verdad… y eso haremos en este capítulo dedicado al Cálculo Proposicional. Sigamos el razonamiento y las explicaciones de Don José…

Si estamos hablando de Cálculo Proposicional, es decir, Cálculo de Proposiciones, lo primero que habrá que definir es qué es para nosotros una Proposición: Una frase a la que podemos atribuir, sin el menor asomo de duda, un valor de Verdad o de Falsedad.

Atención: “Podemos atribuir” no indica que tengamos que saber exactamente si la frase es verdadera o falsa en un contexto, sino que tenemos los medios para saberlo. Por ejemplo, la frase “Está lloviendo” es una proposición a la que podemos asignar sin duda alguna un valor de verdad o falsedad… una vez que hayamos mirado por la ventana.^[1]

Entonces, frases del estilo “La frase que está Vd. leyendo es falsa” no es una proposición, pues no podemos asignarle un valor de verdad ni de falsedad ni de nada de nada, salvo quizá acordarnos amablemente de los ancestros del autor de la frase. En una palabra, el cálculo proposicional no es pertinente para tratar frases de esas tan comunes que cualquiera calificaría de “Verdades a Medias” o de “Medias Mentiras”, que para el caso es lo mismo. No es, por lo tanto, una herramienta adecuada para analizar frases y afirmaciones de políticos, economistas, abogados… Si lo hacemos llegaremos continuamente a contradicciones y sinsentidos, así que mejor dejar el análisis de sus afirmaciones a avezados analistas y tertulianos varios, aunque me dé la sensación de que acertarían más leyendo los posos del té… En fin, dejemos este espinoso tema para esos avezados analistas y tertulianos que nos siguen, y centrémonos en el cálculo de proposiciones, de ésas de las que con todo rigor podemos estar seguros si son verdaderas o falsas…

.

Naturalmente, podemos unir varias proposiciones elementales (del estilo de “Llueve”, “Soy agricultor” o “La Tierra se mueve”) en una proposición compuesta, para lo que tenemos que unirlas mediante nexos. Estos nexos posibles son ni más ni menos que las conjunciones copulativas y/o las disyuntivas. En una palabra, mediante las conjunciones Y y O. Y también podemos negarlas (“No llueve”), mediante la partícula NO.^[2]

Podemos decir, por tanto, que “Llueve Y NO me mojo”, o que “Llueve O me mojo”. En este último caso, y que quede claro de aquí para siempre jamás, decir “Llueve O me mojo” quiere en realidad decir “Llueve O me mojo O ambas cosas”.

Si lo que queremos decir es que “O bien Llueve, o bien Me mojo, pero no simultáneamente”, cosa que en el cálculo proposicional y en la vida real es perfectamente posible, veremos más adelante que eso se trata de un “O lógico exclusivo”, y no de un “O“ normal. Lo digo porque en el lenguaje cotidiano se usa muchas veces el “O” con sentido exclusivo, y todo el mundo lo entiende así. Por ejemplo, si alguien nos pregunta “¿Adónde quieres cenar, en un chino o en un italiano?”, o bien “¿Dónde quieres que vayamos hoy, al cine o al teatro?”, prácticamente todo el mundo entiende que ambas opciones son exclusivas: si vamos al cine queda descartado el teatro y viceversa, y si vamos al italiano, el chino se queda hoy sin algunos clientes… Si a cualquiera de esas preguntas contestas “¡A ambos sitios!” lo más normal es que quien pregunta se quede sorprendido… no espera tal contestación (e incluso puede ser directamente imposible, si ambas actividades son a la misma hora).

Repito para que quede claro, cristalino: En cálculo proposicional, el “O” implica siempre, siempre, “Uno u Otro o Ambos a la vez”. Siempre.

Veamos, pues, usando la ínclita Forma Normal Disyuntiva, que para algo la expliqué hace un tiempo, cómo se comportan estas proposiciones compuestas (aquí, obviamente, V significa “Verdadero” y F, “Falso”):

Llueve	Me mojo	Llueve Y Me mojo
V	V	V
V	F	F
F	V	F
F	F	F

 

 

 

 

 

 

 

 

 

 

Llueve	Me mojo	Llueve O Me mojo [O Ambas]
V	V	V
V	F	V
F	V	V
F	F	F

 

 

 

 

 

 

 

 

 

 

 

A estas tablas tan monas se les denomina, de forma no muy imaginativa pero ciertamente descriptiva, “Tablas de Verdad”, y serán muy importantes en todo lo que sigue.

Tablas de Verdad. Anotarlo en algún rinconcito del cerebro para que no se olvide…

.

También podemos negar una proposición, dando origen a una proposición nueva, como “No llueve”, que será verdadera cuando “Llueve” sea falsa y viceversa. Entonces la tabla de verdad de una negación sería algo tan tonto como:

Llueve	No llueve
V	F
F	V

 

 

 

 

 

En jerga “cálculoproposicionalística”, las proposiciones genéricas que se usan en las fórmulas no suelen designarse con x, y, z… como es habitual en casi todas las ramas de la Matemática, sino más bien con p, q, r…. Además, en lugar de “Y”, “O” o “NO”, se usan los símbolos siguientes: , para el “y”,  para el “o”, y  para el “no”, aunque también se puede usar el símbolo  para denotar la negación; de ambas formas podéis encontrarlo, aunque yo usaré normalmente el signo .

Además, y ya puestos, podemos cambiar la representación de los propios valores posibles, asignando un “1” al valor Verdadero y un “0” al valor “Falso”. En realidad no hemos cambiado nada, tan sólo la forma de escribirlo… Sabiendo esto, podemos reescribir las tablas anteriores de la forma siguiente:

1	1	1
1	0	0
0	1	0
0	0	0

 

 

 

 

 

 

 

 

 

1	1	1
1	0	1
0	1	1
0	0	0

 

 

 

 

 

 

 

 

 

1	0
0	1

 

 

 

 

 

¿De acuerdo? Obviamente, si tenemos varias proposiciones (frases) mezcladas con “o” e “y”, algunas de ellas negadas y otras no, por muy complicada que sea la frase, siempre podemos conocer el valor de verdad de la proposición completa en base a la explotación de la correspondiente tabla de verdad. Muy útiles, las tablas de verdad, como veis.

Por ejemplo, sea la proposición , de la que queremos establecer su tabla de verdad en función de los valores de las proposiciones elementales p, q y r. Para facilitarnos la vida, usaremos algunas variables intermedias: llamaremos s al resultado de la proposición (ahora la fórmula original será , y luego llamaremos t al resultado de .

Construyendo la tabla de verdad paso a paso (tabla que, debido a que son tres las variables, tendrá ocho posibles combinaciones de valores, como supongo os habéis dado cuenta),^[3] llegamos a los valores de verdad resultantes:

1	1	1	0	0	1	1
1	1	0	1	1	1	1
1	0	1	0	0	1	1
1	0	0	1	0	1	1
0	1	1	0	0	0	0
0	1	0	1	1	1	1
0	0	1	0	0	0	0
0	0	0	1	0	0	0

 

NOTA: Podemos obtener con toda sencillez la fórmula equivalente en Forma Normal Disyuntiva de dicha fórmula simplemente explotando la Tabla de Verdad, creo que se ve claro mirando dicha tabla de verdad, ¿no es cierto?

Si queremos, por fin, conocer la tabla de verdad del O lógico exclusivo (lo denominaré 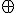por hacerlo de alguna forma; así al menos es como se identifica el XOR en el diseño de puertas lógicas)^[4] al que antes hice referencia (donde es cierta una proposición u otra, pero no ambas a la vez), no es ni más ni menos que la siguiente:

1	1	0
1	0	1
0	1	1
0	0	0

 

 

 

 

 

 

 

 

 

Y su fórmula resultante (en Forma Normal Disyuntiva) será .

.

Bueno, pues ahora sólo queda pensar un poco acerca de la naturaleza íntima de las proposiciones y las operaciones que las afectan… Mmmmm… veamos qué tenemos…

Un conjunto de elementos que pueden admitir sólo dos valores (0, 1), y dos operaciones cerradas que operan sobre ellos ()… Mmmmm… Esto me suena. ¿No será esto, por una casualidad, un álgebra de Boole?

.

Vamos a comprobarlo, y para ello habrá que verificar si todo este sistema cumple los axiomas de Huntington (1904). En el primer capítulo de la serie conté cuáles eran estos axiomas. Id allí si queréis refrescarlos.

Habría que comprobar, sucesivamente, si las operaciones “Y” y “O” referidas a proposiciones que pueden ser Verdaderas o Falsas exclusivamente (ya sabéis, eso de las “Verdades a Medias” no funciona muy bien en Cálculo Proposicional) cumplen los cuatro axiomas. No voy a detallar paso a paso las demostraciones, dejando al lector, si lo desea, probar los axiomas uno a uno, demostrando si se cumplen o no. Para ello utilizará seguramente las correspondientes tablas de verdad que tan útiles son…

Uno: ¿Son las operaciones “Y” y “O” conmutativas? Pues sí, lo son. Intuitivamente, parece que igual da decir “Llueve o Me mojo” que “Me mojo o Llueve”…

Dos: ¿Tienen las operaciones un elemento neutro? Evidentemente. El valor “Falso” (0) es el elemento neutro del “O” (“Llueve O Cualquier Cosa Falsa”^[5] es equivalente a “Llueve”, pues tiene su misma tabla de verdad), mientras que el valor “Verdadero” (1) es el elemento neutro del “Y” (“Llueve Y Cualquier Cosa Verdadera”^[6] es equivalente a “Llueve”, pues también tiene su misma tabla de verdad).

Tres: ¿Cumplen las operaciones la propiedad distributiva? Esto es menos evidente, pero si construís las tablas de verdad, veréis que, efectivamente, se cumple a rajatabla la propiedad distributiva, tanto del “Y” respecto del “O”, como del “O” respecto del “Y”.

Cuatro: ¿Tiene cada elemento un complementario? Esto sí que es sencillo: al haber sólo dos valores posibles, es sencillo ver que “Verdadero” es el complementario (el contrario) de “Falso”, y viceversa.^[7][8][9]

Por lo tanto, Señoras y Señores, el cálculo proposicional es un álgebra de Boole. Y yastá.

Todos los artilugios, teoremas y procedimientos que funcionan para un álgebra de Boole funcionan también en Cálculo Proposicional. Hala! Ya sabemos bucear entre Verdades y Mentiras…

.

Ya os podéis imaginar que todo esto es vital para poder diseñar y escribir programas eficientemente.

Efectivamente, todo aquél que haya escrito un  programa en su vida (y eso incluye haber metido alguna fórmula medianamente compleja en una hoja electrónica) ha tenido que lidiar con el famoso “IF“. El “Si” condicional que gobierna el flujo de los programas.

Muchas veces sirve escribir el if consultando una única proposición. Por ejemplo, en un cajero automático: Si el saldo de la cuenta es menor que el dinero que el cliente desea llevarse, denegar la operación. Fácil

Pero es muy normal tener que lidiar con proposiciones complejas que hay que evaluar para decidir por dónde debe seguir el programa…

Verbigracia:  Si el cliente es nuevo y tiene una marca de captación mayor de 7, o, siendo antiguo, tiene un saldo superior a x Euros y no tiene ninguna marca de “Cliente especial” siempre que el director de la sucursal no le haya calificado como de tipo 1 ó 3, o bien el director de la regional le haya calificado como de tipo 6, pero no de tipo 9, y además está como titular en una cuenta en la que alguno de los otros titulares sea un cliente preferente… entonces le concedemos el préstamo.

(!!)^[10]

Estaréis pensando… ¡qué condiciones tan retorcidas se ha sacado de la manga el Macluskey…! Pues no, amigos, no. Cosas mucho más complicadas todavía he tenido que escribir a lo largo de mi vida profesional… Y lo peor no es que esa condición sea alambicada, no: lo peor es que ¡Hay que programarla!, es decir, hay que escribir un programa que refleje fielmente esa condición de negocio. Y no sólo tiene que reflejar con fidelidad la condición de negocio, sino que tiene que hacerlo de la manera más simple y eficaz posible. Es más, de éstas habrá muchas, pero muchas, en cualquier Sistema que se precie…

¿Os dais cuenta ahora de lo importante que resulta conocer el Cálculo Proposicional para poder hacer esto correctamente?

La de programas que han fallado miserablemente por no tener correctamente programado el “if” correspondiente… Es, con gran diferencia, el principal motivo de fallo de los programas de todas partes: un if mal programado.

El verbo “IF” es el usado universalmente para designar la instrucción condicional; luego, según el lenguaje de programación usado, se escriben de una forma u otra tanto las comparaciones que forman las proposiciones individuales^[11] como las uniones entre ellas: Y (que casi siempre se pone en inglés: AND), O (lo mismo: OR) o NO (NOT),.

En Cobol, por ejemplo, se usan en inglés tal cual (AND, OR, NOT), lo mismo que en otros muchos lenguajes, como en SQL, pero en C, por ejemplo, igual que en Java o en PHP, se usa && para el Y, || para el O y ! para el NOT,^[12] y en Excel, versión española, se usa O(a,b,…), Y(a,b,…) y NO(a), y así.

Obviamente, la misma explicación sirve para las condiciones de terminación de los bucles DO-UNTIL o DO-WHILE, así que me ahorro seguir.

Y hoy en día hay muchísimos componentes y mecanismos industriales (como la alarma que funciona según el diagrama de la derecha) que tienen empotrado un software… un software casi siempre llenito de IF’s…

Bueno, pues ahora ya sabéis que, como todo esto es un álgebra de Boole, puedes aplicar todas sus reglas (que son las mismas del Cálculo Proposicional) para simplificar el contenido del if, o bien usar su FND para tratar de comprender uno que ya está programado.

Como bien dice J, “Ay, si me hubieran dado un mísero euro por cada vez que me he encontrado un if kilométrico^[13] que siempre era “true” (verdadero) o siempre era “false” (falso, claro),  o bien que se podía simplificar a uno mucho más sencillo“…

.

Ya para acabar, dije antes que, como el Cálculo Proposicional forma un álgebra de Boole,  ya sabemos bucear entre Verdades y Mentiras… pero no. No del todo.

Los humanos somos tan raros hablando y formulando frases, que hay que profundizar un poco más para poder usar esta herramienta en proposiciones formales. Pero eso lo iremos viendo en siguientes capítulos, que éste va quedando largo. Para empezar, hablaremos de la implicación lógica, la dichosa y a priori tan poco comprendida implicación lógica. A ver si, antes simplista que incomprensible, consigo explicarme y que se entienda tan “enrevesada” cosa, y por qué es como es y no de otra manera… Siento el suspense, pero no queda otra que esperar hasta el siguiente capítulo de “Eso que llamamos Lógica”, próximamente en sus pantallas…

.

NOTA IMPORTANTE

… para poder seguir el resto de la serie sin perderse.

Dije al principio del artículo que el método seguido por José Cuena para enseñarnos Lógica, dentro de su asignatura de “Metodología”, se basaba en introducir poco a poco los conceptos teóricos de lo particular a lo general, de tal modo que cada concepto explicado tuviera siempre otros conceptos en los que asentarse. En un símil del mundo de la construcción, primero definía cómo hacer un ladrillo, luego cómo construir una pared con ladrillos, luego cómo construir una habitación a base de paredes, una casa a base de habitaciones, una urbanización a base de casas…

Este método se denomina en la jerga informática “bottom-up“, de abajo arriba, de lo particular a lo general, en contraposición al método “top-down“, de arriba abajo, que funciona exactamente al revés: de lo general a lo particular. Ambos métodos funcionan, claro, pero bajo mi modestísimo punto de vista, en la enseñanza de cualquier tipo de temario se debe preferir el método “bottom-up”. Por ejemplo, antes de enseñar al niño a leer palabras completas se le enseña a leer letras individuales, y antes de leer frases, se le enseña a leer palabras. Y antes de enseñar a multiplicar, se enseña a sumar…

Todo esto puede parecer evidente, obvio, casi de Perogrullo. Pero resulta que, para lo que viene a continuación, para la exposición de los intríngulis de la Lógica, este sistema “bottom-up” puede resultar contraproducente, puede dificultar la comprensión de lo expuesto en cada momento. No es que falte nada, que no falta, está todo, todo, pero… no sé cómo decirlo, descolocado, desordenado… al menos desde cierto punto de vista.

Me he dado cuenta de ello, poco a poco, en los intensos debates^[14] que hemos mantenido Pedro, J y yo durante la revisión de los artículos de la serie. Ellos ponían pegas, porque no entendían ni las explicaciones ni los ejemplos, no porque estuvieran mal, sino porque les faltaban cosas obvias para ellos que yo (o sea, Pepe Cuena) estaba pasando por alto… Luego, al revisar el siguiente artículo, decían: “Ah!, claro, es que lo que yo echaba en falta en el artículo x, lo explicas luego en el artículo x+1, o en el x+2…“.

Disculpadme: No puedo ser mucho más preciso al respecto si no quiero destripar lo que queda de serie; sólo contaros que estos malosentendidos son debidos fundamentalmente, según mi entender, a la diferencia entre su formación (de J y de Pedro) y la mía: mientras su enorme formación es de corte marcadamente científico, la escasa mía es más bien de corte generalista: ellos echaban en falta, necesitaban para entender bien los conceptos que las cosas se expusieran de un modo diferente, mejor, en un orden diferente al que se exponen en la serie. Y hasta aquí puedo leer…

En fin, tras todos estos intensos intercambios, he modificado sustancialmente los artículos para, sin perder esa orientación “bottom-up” ni destripar nada de lo que quede ni usar nada que no haya sido explicado, ir dando al lector las armas para ir siguiendo la explicación y que no se pierda en disquisiciones que serán resueltas más adelante.

O sea: no voy a dar por sentado nada. Nada de nada. Voy a ir avanzando pasito a pasito por el proceloso mundo lógico hasta llegar a su glorioso final. Pero, por favor, creedme, ¡no os impacientéis! Cuando acabe la serie, todo lo necesario para razonar e inferir cosas a partir de otras estarán explicadas, desde lo particular a lo general, “bottom-up”. Nada faltará, el círculo estará cerrado, todo encajará.

Como si fuera una buena novela de suspense, por favor, seguid la exposición, aceptar las cosas como las iré contando y en el orden en que las iré contando, y el final seguro que os satisfará. Pero, permitidme que insista… ¡No   Os   Impacientéis!

.

Disfrutad de la vida, mientras podáis.

1. Aunque hay veces que no sé yo… como decía un amigo mío sevillano, preguntado sobre el tiempo que hacía cierto día en Sevilla: “Llover, llover, lo que se dice llover… llueve. Pero llover, llover, lo que se dice llover… pues ¡no llueve! ¡Ah, qué maravillosa riqueza la del idioma español! [↩]
2. La conjunción NI, que es copulativa también, en realidad es la suma de NO y de Y, así que en realidad no es atómica. [↩]
3. Por ser 2 (estados) elevado a 3 (variables). [↩]
4. Su nombre “de guerra” es Exclusive Or, en inglés. Aunque en realidad todo el mundo se refiere a él por su abreviatura: XOR, que es como se llaman normalmente las instrucciones de ordenador que lo implementan. [↩]
5. Cualquier Cosa Falsa sería una proposición que resulte siempre falsa, como por ejemplo “Macluskey tiene menos de treinta años”… ¡quién los pillara! [↩]
6. Cualquier Cosa Verdadera sería una proposición que resulte siempre verdadera, como por ejemplo “Macluskey tiene más de treinta años. [↩]
7. Truco para descreídos: cuando hablé de circuitos eléctricos en el tercer capítulo de la serie, sí que demostré con santa paciencia todos y cada uno de los dichosos axiomas. Si vais allí y cambiáis “Cerrado” por “Verdadero”, y “Abierto” por “Falso”, y además cambiáis “En Serie” por “Y” y “En Paralelo” por “O”, pues ya lo tenéis todo demostrado. [↩]
8. Bueno, en realidad, lo que ocurre es que las estructuras matemáticas subyacentes a la Lógica Proposicional son las mismas que la de los Circuitos eléctricos. [↩]
9. … Uff ¿A ver si va a ser verdad que al final las máquinas dominarán el mundo…? [↩]
10. Con razón se conceden tan pocos préstamos. [↩]
11. En el ejemplo, Cliente Nuevo=SI; Marca de Captación>7; Saldo>X; Tipo de Cliente=1; etc, etc. [↩]
12. Que ya son ganas de molestar, con lo fácil que es lo de AND, OR, NOT… [↩]
13. Por supuesto, siempre escrito por otros, claro, faltaría más, no iba yo a hacerlo mal… [↩]
14. Y esta vez, cuando digo intensos, es que han sido intensos. [↩]