El Cedazo

Siguiendo la línea de esta serie, observamos, en el artículo anterior, los inicios de la gran revolución que siguió a la proposición del modelo heliocéntrico de Copérnico-Kepler. Con este modelo, en 1618, se obtuvo la teoría de proporciones que hoy conocemos como la tercera ley de Kepler. Con ella y el método de medición de la paralaje con observatorios sobre la superficie terrestre (paralaje diurna) la humanidad  resolvió no sólo el problema de nuestra distancia al Sol sino a los demás planetas.

A pesar de la gran excitación que causó en la comunidad científica, tal método resultó no ser aplicable a las estrellas. Por más alejados sobre la superficie terrestre que estuviesen los observatorios, no se veía variación angular entre las mediciones que hacía cada observador de la posición de cualquier estrella. Ello no debería ser sorprendente, pues con los instrumentos disponibles hacia el siglo dieciocho incluso la paralaje medida de Saturno era nula por más que los astrónomos se empeñaran en ser minuciosos. Para muchos, una situación algo desmotivante. No obstante, la creatividad humana no se quedó allí y no sólo la medición de distancias a las estrellas fue posible,  sino indirectamente otros fenómenos desconocidos y que actualmente son de gran interés. De ello vale la pena hablar hoy.

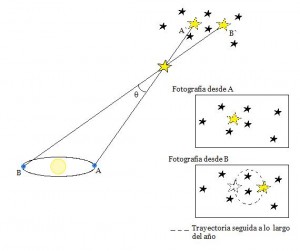
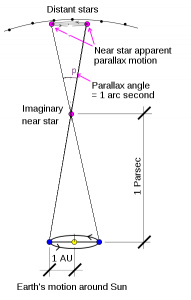
Paralaje estelar: durante medio año la Tierra gira alrededor del Sol y la posición de la estrella en estudio cambia con respecto a las estrellas lejanas. La paralaje sería el ángulo θ en el que difieren las mediciones hechas. (Autor)

A pesar del desolador panorama que se presentaba a los astrónomos, la superficie de la Tierra no constituía el último recurso para la resolución del problema. El método de la paralaje diurna permitió ver que la Tierra describía una órbita alrededor del Sol con un diámetro de unos 299.000.000 km, de modo que, como se ve en la imagen a la derecha, si se registraba la posición de una estrella una tarde y otra tarde se volvía a registrar, pero medio año después, el nuevo punto de observación estaría no a un diámetro terrestre, sino a 23.600 veces esta distancia. La paralaje se vería, por tanto, multiplicada por el mismo factor.

Tal método (llamado de paralaje estelar o anual para diferenciarlo del método de paralaje diurna) no se puede aplicar a los planetas, pues estos, a lo largo de medio año terrestre, describen una trayectoria tan complicada que cualquier desplazamiento paraláctico originado por el movimiento de la Tierra quedaría enmascarado. Los resultados obtenidos por este método, al aplicarlos a los planetas, indudablemente serían mucho menos exactos que con el método ordinario. Las estrellas, por el contrario permanecen relativamente fijas durante todo el año, lo cual da esperanzas de observar un desplazamiento útil. La primera persona que no sólo propuso este método sino que  intentó medir estas paralajes es un viejo conocido: el genial Aristarco de Samos.^[1] Sus mediciones a simple vista no le dieron los resultados esperados. Lastimosamente, mil novecientos años y muchas lentes de aumento después, tal paralaje tampoco fue observada en ninguna estrella. Llegó la década de 1830 y la paralaje seguía esquiva. Veamos las razones del fracaso.

La ausencia de paralajes fue inquietante desde tiempos de Aristarco. Lo primero que se pensó fue que la Tierra, después de todo, no se moviera con respecto a las estrellas y Copérnico y Kepler (y Aristarco para los que conocían sus escritos) estuviesen equivocados. En este caso, luego de un año, no se observaría paralaje alguna. Aristóteles, férreo defensor de la teoría geocéntrica, esgrimió tal argumento en contra de un posible movimiento de la Tierra alrededor del Sol. Sin embargo, para el siglo XVIII, el éxito del modelo heliocéntrico era enorme y ya era claro que la Tierra sí se mueve. La ausencia de paralaje debía explicarse de otra forma.

La paralaje estelar sólo es detectable si las estrellas no están equidistantes a la órbita terrestre. Movimiento a lo largo de un año debido a la paralaje, a varias distancias, de una estrella sobre la eclíptica.

Las respuestas empezaron a barajarse: desde los tiempos de Hiparco de Nicea, el cielo era imaginado como una cúpula en la cual estaban las estrellas algo así como pintadas. De esa manera todas se encontrarían equidistantes de la Tierra. Sabemos que el método de paralaje necesita de un fondo alejado y heterogéneo que sirva como referencia; al estar todas las estrellas a la misma distancia, por definición tal fondo no existe. Pero ¿podría aceptarse esta teoría? Con el tiempo, se fueron descubriendo varias razones que llevaban a pensar que la distancia de las estrellas a la Tierra era variable. De ser así, éstas se distribuirían uniformemente por todo el espacio y el Universo no tendría frontera rígida.

Lo primero que se pensó fue que las estrellas no estarían equidistantes, pues no todas son igual de brillantes. Hiparco se preocupó por este fenómeno e hizo el primer intento de clasificar las estrellas visibles sin instrumentos, de acuerdo a su brillo. Construyó una escala de seis magnitudes, siendo la primera la correspondiente a las de brillo más intenso y la sexta asignada a las apenas visibles. Trabajo descomunal, pues es una tarea realmente difícil para el ojo humano discernir con precisión aceptable la magnitud del brillo de las estrellas. Actualmente los astrónomos miden la intensidad de tal brillo con precisión matemática e instrumentos de los que no disponían los griegos. De esta forma, fue posible construir el sistema actual de clasificación estelar (llamado sistema de medición de magnitud aparente). Este sistema es muy similar al de Hiparco pero proporciona mayor precisión. En él, una diferencia de 5 magnitudes (por ejemplo, de 1 a 6) representa un cociente de 100 medido en brillo. Es decir, una estrella de magnitud 1 sería 100 veces más brillante que una de magnitud 6. De esta forma, una diferencia de una magnitud representa un cociente de aproximadamente 2,512^[2].

Estrellas de la constelación Leo por orden de brillo.

Tal es la precisión actual que permite darle décimas de unidad a la magnitud del brillo de una estrella. De esta forma, por ejemplo, Aldebarán (o Alpha-Tauri)^[3] tiene un brillo de magnitud 1,1. Existen estrellas que vemos más brillantes que Aldebarán y por lo tanto de magnitud inferior a 1,0. Por ejemplo, Procyon (Alpha-Canis Minoris) tiene una magnitud de 0,5, Vega (Alfa Lyrae) más brillante aun, de 0,0.^[4] Incluso existen estrellas de magnitud negativa, como Sirio (Alfa-Canis Majoris) que, con una magnitud de brillo de  -1,4, es la más brillante de la bóveda celeste. También puede asignarse una medida al brillo de los planetas, la Luna y el Sol. Júpiter llega a alcanzar una magnitud de -2,5, Marte de -2,8 y Venus de -4,3. La Luna tiene un brillo de magnitud aparente de -12,6 y el Sol de -26,9. Por otro lado, si nos vamos a los objetos más tenues que podemos medir, el telescopio espacial Hubble, el más potente en el espectro óptico, ha conseguido distinguir estrellas de magnitud 30.

Si suponemos que todas las estrellas tienen el mismo brillo, cabría concluir que la diferencia en el brillo aparente se debe únicamente a la distancia a la que la estrella se encuentra de nosotros. Las estrellas más cercanas serían más brillantes y las lejanas, más tenues. A pesar de ser éste un argumento para refutar la teoría de la bóveda celeste, nada en 1700 permitía suponer que las estrellas tuvieran el mismo brillo propio. Podía ser también que estuviesen todas a la misma distancia y su diferencia de brillo fuese una diferencia real.

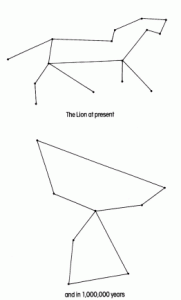
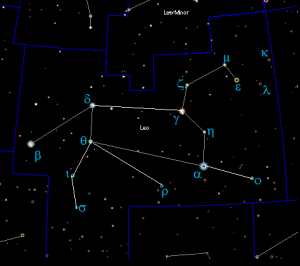
Movimiento propio de las estrellas de la constelación Leo a lo largo de un millón de años. (Carl Sagan: cosmos)

Otro argumento en contra de la suposición de la bóveda celeste vendría también desde tiempos de la Grecia Helenística. Los astrónomos de Alejandría habían registrado la posición relativa de una gran cantidad de estrellas. En el mapa estelar que mostraba el brillo de las estrellas, Hiparco incluyó también la posición de más de 800 estrellas en el cielo de sus tiempos. Este mapa fue preservado y ampliado por Ptolomeo, quien añadió unas 200 estrellas más. Más de mil ochocientos años después, en 1718, el astrónomo inglés Sir Edmund Halley, a quien debemos la descripción de la naturaleza de los cometas, observó que por lo menos tres estrellas (Sirio, Procyon y Arturo) ocupaban un lugar diferente al asignado por Hiparco. La diferencia era tan grande que la posibilidad de que los griegos o Halley se hubiesen equivocado era muy remota. Por ejemplo, Arturo (Alfa Bootis) se había desplazado un grado (dos veces el diámetro de la Luna) del lugar que le habían asignado los griegos. Halley concluyó que las estrellas se habían movido, tan lentamente que su movimiento no era perceptible en un año pero sí luego de muchas generaciones. Estas observaciones daban un gran golpe a la hipótesis de la bóveda fija pues se veía que algunas, si no todas las estrellas, no estaban sujetas a la bóveda. El movimiento de una estrella que observamos con respecto a las demás lo llamaremos movimiento propio. Actualmente se han realizado mediciones de movimiento propio de muchas estrellas, como en la figura de la izquierda, que muestra el movimiento propio de las estrellas de la constelación Leo adelantándonos un millón de años en el futuro.

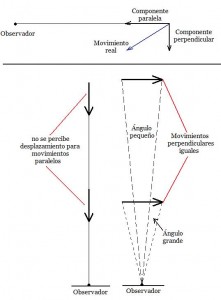
Movimiento relativo de las estrellas en relación con las componentes de movimiento con respecto a la linea de observación (Autor)

Si suponemos que la estrellas se encuentran distribuidas a distancias variables, lo más lógico es pensar que todas ellas se mueven a velocidades más o menos iguales y en direcciones aleatorias. Con esto podemos llegar a conclusiones interesantes. Si suponemos una dirección aleatoria de movimiento y separamos su movimiento, como en el dibujo de la derecha, en componentes paralela y perpendicular a la línea de visión del astrónomo, podemos decir que, en promedio, la mitad de las estrellas tienen en su movimiento una mayor componente perpendicular, mientras que la otra mitad tiene un movimiento con mayor componente paralela a ésta. Como se ve en la imagen, ninguna de las estrellas que se mueven con una gran componente en dirección paralela a la línea de visión presentaría movimiento propio mensurable, así sean cercanas o lejanas. Por otro lado, de las que se mueven en dirección perpendicular a dicha línea, las más próximas poseerán un movimiento propio mayor que las lejanas.

Esta asociación de movimientos propios grandes viene apoyada por el hecho que precisamente las estrellas más brillantes son las que tienen movimientos propios mayores. Las tres primeras estrellas en que se detectó un movimiento propio—Sirio, Procyon y Arturo—figuran entre las ocho más brillantes del cielo.^[5] Si la estrella es cercana, no sólo presentará un movimiento propio apreciable, sino un brillo aparente mayor. Según este argumento serían muy pocas las estrellas que presenten movimientos propios mensurables.^[6]

Movimiento propio de la estrella de Barnard a lo largo de veinte años (Wikipedia)

A pesar de eso, hacia 1700 nada permitía conocer la velocidad real de una estrella. Actualmente, por ejemplo, el movimiento propio más rápido lo posee la “Estrella de Barnard” descubierta en 1916 por el estadounidense Edward Barnard (1857-1923). Cada año la estrella se mueve, con respecto a las demás estrellas, un ángulo de 10,3 segundos de arco. Para los que no estén familiarizados con este término, recordemos que la circunferencia se divide, angularmente en 360 partes iguales llamadas grados, cada grado en 60 partes llamadas minutos, y cada minuto en 60 partes llamadas segundos. De esta forma, un segundo de arco representa 1/1.296.000 del circuito celeste. La Luna tiene un tamaño aparente de aproximadamente 31 minutos de arco. De esta forma, la estrella de Barnard se movería 1/186 del diámetro de la Luna cada año (!!)^[7]. Tal movimiento, medido en el lapso de 20 años, puede verse en la figura de la izquierda.

Los astrónomos, en un principio, no sabían cómo medir la velocidad real de la estrella pero, para hacer cuentas, podemos suponer que la estrella de Barnard viaja de forma perpendicular a la línea de visión del astrónomo a la misma velocidad que la Tierra (en realidad, su velocidad es de unas cinco veces, y no se mueve perfectamente de forma perpendicular a la tierra, por lo que estamos siendo humildes) es decir, unos 29 km/s. En un año habrá recorrido 940.000.000 km. Para que tal distancia corresponda tan sólo a 10,3 segundos de arco, la estrella de Barnard debería encontrarse a unos 16.000.000.000.000 km de distancia (!!) es decir, miles de veces más lejos que el planeta Neptuno del Sol. Con estas cuentas, la paralaje que exhibiría sería de apenas 1 segundo de arco. Detectar estas distancias angulares minúsculas sería como intentar ver una moneda desde una distancia de seis kilómetros. La distancia de la que hablamos es tan abismal que para que un objeto sea visible desde tan lejos debe ser un cuerpo luminoso más o menos del tamaño de nuestro Sol. Dicho de otro modo, no hay más que pensar que las estrellas son como el Sol y su única diferencia es que las vemos desde una distancia miles de veces más alejada que él.

Tales distancias, aunque fueron aproximaciones menores a las mediciones reales que llegaron muchos años más tarde, dejaron perplejos a los astrónomos. Se puede pensar que la estrella de Barnard en realidad no se mueve tan rápido con lo que llegaríamos a una cifra menor, sin embargo, podemos llegar a conclusiones parecidas por otro medio: supongamos que Sirio, la estrella más brillante, es idéntica en tamaño y en luminosidad a nuestro Sol (realmente es unas 25 veces más brillante). Mientras Sirio tiene un brillo de magnitud aparente -1,6, el del Sol de -26,9, es decir, su diferencia en magnitud es de 25,3. Puesto que un número en magnitud significa un factor de 2,512, el Sol tiene 13.200.000.000 veces más brillo que Sirio. Ahora bien, el brillo de una fuente luminosa varía en proporción del inverso del cuadrado de la distancia es decir, una estrella situada al doble de distancia de otra disminuirá su brillo en (1/2)² ó 1/4. Para que Sirio resplandezca con un brillo 1/13.200.000.000 del Sol, deberá estar 115.000 veces más lejos de la Tierra que éste. Si tomamos la distancia Tierra-Sol como la medida por el método de paralaje diurna  llegamos, nuevamente, a una distancia de 16.000.000.000.000 km. Es decir, sea cual fuere el argumento, las distancias que nos separan de las estrellas más cercanas deben ser realmente abismales, y debido a esto encontraríamos unas paralajes infinitamente pequeñas.

Vemos que es necesario manejar cantidades con varios ceros si necesitamos referirnos a alguna distancia interestelar. Para no tener que leer tantos ceros, acá les ayudo. Los astrónomos, para medir longitudes interestelares, utilizan el patrón año luz. Por definición, es la distancia que recorre un pulso de luz en un año. Recordando que la velocidad de la luz en el vacío es de 300.000 km/s, luego de un año habrá recorrido algo menos que unos diez billones de kilómetros.^[8] Así que nuestro valor supuesto de distancia a Sirio de 16 billones de kilómetros serán aproximadamente unos 1,6 años luz. Si esta estrella es de las más cercanas, es lógico suponer que todas las distancias estelares serán del orden de varios años luz.

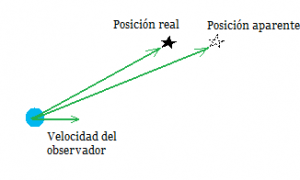
Aberración estelar: la posición aparente de un objeto cambia como resultado de moverse con respecto a él. (Autor)

Volviendo a la medición de paralajes estelares, durante el siglo dieciocho los instrumentos mejoraban enormemente. Sin embargo, con el pasar del tiempo, la cosa, en vez de mejorar, parecía ponerse más peluda. Ya vimos que las estrellas más cercanas son las que más movimiento relativo tienen. Así, al momento de medir paralajes era necesario discriminar tal movimiento de las medidas paralácticas^[9]. La cosa se ponía más compleja: en 1725, el astrónomo inglés James Bradley (1693-1762) observó un efecto que hoy llamamos aberración astronómica, debida principalmente a la velocidad finita de la luz y al movimiento de la Tierra.^[10] Básicamente se puede explicar con el dibujo a la derecha. Para hacerlo más gráfico: Supongamos que anda lloviendo. Una gota de lluvia, aunque caiga verticalmente con respecto a un observador en reposo en la tierra, cae en ángulo para un observador en movimiento y mientras más rápido vaya el observador, mayor será el ángulo. Precisamente eso es lo que le pasa a la luz cuando observamos a una estrella, pues, en nuestro caso, es la propia Tierra el observador en movimiento. La trayectoria de la luz se modifica y observaremos a la estrella en diferente posición dependiendo de la velocidad relativa de la Tierra con respecto a la estrella. Obviamente, como el movimiento de la Tierra es periódico, este efecto es también anual como el de la paralaje, pero depende el ángulo con respecto al plano de la eclíptica (el plano de órbita de la Tierra con respecto al Sol) que tenga la estrella, algo que no se ve en la primera. 

Nutación del eje terrestre en torno a la trayectoria de precesión.

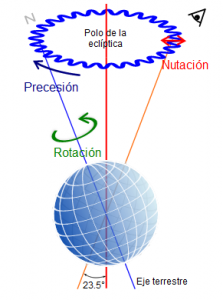
Bradley también descubrió que la dirección del eje de la Tierra respecto a las estrellas oscila ligeramente con un periodo de dieciocho años y medio. Este fenómeno de cabeceo del eje de rotación es llamado nutación. Como consecuencia de este cabeceo, la posición aparente de las estrellas con respecto a un observatorio en la superficie terrestre cambiará, produciendo una trayectoria irregular a lo largo de esos dieciocho años y medio, al cabo de los cuales volverá a su sitio original.

La búsqueda de paralajes estelares se volvía cada vez más esquiva, pero los instrumentos seguían mejorando. Esta vez otro viejo conocido, William Herschel (quien descubrió a  de Urano) se dio cuenta de otro fenómeno de gran interés. Siguiendo la sugerencia de Galileo, los efectos paralácticos deberían ser medidos más fácilmente comparando dos estrellas muy próximas angularmente entre sí, seguramente una estaría muy lejos y la otra mucho más cerca. De esta forma, la paralaje era mucho más fácil de medir teniendo en cuenta las posiciones relativas de cada estrella. Herschel, comparando estrellas muy cercanas en la línea de visión, detectó desplazamientos que no podía atribuir a paralajes estelares. Los efectos paralácticos deberían producir una elipse completa al cabo de un año, cosa que los movimientos detectados por Herschel no cumplían. A pesar de que estos movimientos también describían elipses, éstas no se completaban sino después de un periodo mucho mayor.

Sistema binario de dos estrellas de masa similar. (público)

En 1793 Herschel llegó a la conclusión de que estos movimientos se debían al giro de dos estrellas en torno a su centro de gravedad, y que el par de estrellas no eran sistemas independientes, uno mucho más alejado del otro y que por coincidencia parecían cercanos, sino que efectivamente ambas estrellas estaban muy cerca una de la otra. Este genial astrónomo había descubierto las estrellas binarias. A lo largo de los años descubrió otros 800 sistemas binarios, y actualmente es tal la cantidad de sistemas binarios que se han encontrado que los astrónomos sugieren que el 75% de las estrellas que vemos corresponden a sistemas de dos o más estrellas.

El sistema doble: Sirio A, la más grande, junto a su compañera Sirio B, mucho más pequeña. (Telescopio espacial Hubble)

Pero las consecuencias del descubrimiento de Herschel no pararían allí. En 1844, el astrónomo alemán Friedich Wilhelm Bessel (1784-1846), estudiando la estrella Sirio, comprobó que su movimiento propio no era simplemente una recta, sino una línea ondulada. Si hubiese una estrella al lado de ella podría decirse que tal movimiento era debido a la rotación de Sirio en torno a tal estrella. Pero no se observó ninguna compañera en sus alrededores. Bessel sugirió la presencia de una compañera oscura, es decir, una estrella de masa apreciable pero sin brillo, que ejerciera su fuerza gravitatoria sobre Sirio. Tal idea se vio confirmada en 1862 con el descubrimiento por parte del astrónomo estadounidense Alvan Graham Clark (1832-1897) de un punto muy tenue cerca de Sirio. Ésta sería la compañera oscura de Sirio (hoy llamada Sirio B), aunque después de todo no resultó ser tan oscura, pues su magnitud era de sólo 7,1. Podemos ver en la imagen de la derecha una comparación de sus brillos.

Una vez conocidos los fenómenos más importantes que conducían a problemas en la medición de paralajes estelares, así como el refinamiento gradual de los instrumentos, la esperanza de medirlas aumentaba. Finalmente, en los años 1830-39, se abordó el problema desde tres puntos diferentes del planeta y de manera independiente. En Sudáfrica, el astrónomo escocés Thomas Henderson (1798-1844) se dedicaba a estudiar la estrella Alpha-Centauri,^[11] estrella de gran brillo que hacía suponer a Henderson que se encontraba muy cerca. A orillas del mar Báltico, el germano-ruso Georg Wilhem von Struve (1793-1864) registraba la posición de Vega (Alpha- Lyrae). Por su lado, en Könisberg, Prusia oriental, Bessel (antes de descubrir la compañera de Sirio) no medía estrellas brillantes, sino estrellas veloces. Según este criterio, escogió la estrella 61 Cygni la cual tiene un movimiento propio de 5,2 segundos de arco por año, en aquel entonces la más veloz conocida. Hacia 1838 los tres astrónomos habían llegado a conclusiones importantes. Bessel fue el primero en publicarlas en1838; luego Henderson, quien tuvo que esperar a volver a Inglaterra, y por tanto no los publicó hasta 1839; finalmente Struve hizo lo propio en 1840.

Luego de mejoras subsiguientes de los resultados originales, se vio que Alpha-Centauri constituía un sistema triple: dos estrellas del tamaño del Sol muy próximas entre sí y la tercera (posteriormente llamada Próxima-Centauri), muy alejada de la pareja y muy tenue, y que es considerada actualmente la estrella más cercana a nuestro sistema solar. Debido a que su movimiento con respecto a la Tierra tiene una considerable componente paralela a la línea de observación, su movimiento propio es menor al de la estrella de Barnard (Sin embargo puedes verlo aquí). Tal sistema tiene una paralaje de apenas 0,76 segundos de arco resultando ser el mayor de los detectados a la fecha. Así, el sistema más cercano al nuestro es Alpha-Centauri, situado a 4,29 años luz. En cuanto a 61 Cygni, se comprobó que era un sistema doble. Resultó tener una paralaje de unos 0,29 segundos de arco y por lo tanto, encontrarse alejada de nosotros unos 11,1 años luz. Vega, en cambio, tuvo una paralaje mucho más difícil de medir, pues resultó estar alejada de nuestro sistema solar unos 27 años luz.

Definición de pársec

Una vez determinadas las paralajes a las estrellas más cercanas, se hizo popular una nueva unidad de distancia introducida por el astrónomo inglés Herbert Hall Turner (1861-1930), quien pensó que una unidad adecuada sería la distancia a la cual una estrella presenta una paralaje de un segundo de arco. Esta unidad es la paralaje-segundo abreviada como parsec. Una parsec es unos 3,26 años luz o 200.000 unidades astronómicas,^[12] o 30 billones de kilómetros.

Ahora bien, si conocemos la distancia real de una estrella es posible calcular su luminosidad a partir de su magnitud aparente; o a la inversa, determinar qué brillo presentaría a una distancia dada. El brillo aparente de una estrella a la distancia (arbitraria) de 10 parsecs (o 32,6 años-luz) se denomina magnitud absoluta de la estrella. Por ejemplo, si colocamos nuestro Sol a 10 parsecs tendría una magnitud de 4,9 y sería una estrella muy tenue. Si colocáramos a Sirio a tal distancia en vez de los 2,7 parsecs a que se encuentra, su brillo sería lógicamente más tenue del que vemos desde la Tierra, pero aún así sería de 1,4.^[13] En otras palabras: el Sol, el objeto más glorioso de nuestro cielo, y que Copérnico consideraba como centro del universo, no sólo es una estrella como las demás, sino que es una estrella común. Hay otras estrellas miles de veces más brillantes que ella. Sin embargo, no hay por qué sentirnos cohibidos. De las cincuenta estrellas más cercanas a nuestro sistema solar, sólo tres—Sirio, Procyon y Altair—son más luminosas que él. Las dos estrellas del sistema Alpha-Centauri son aproximadamente igual de luminosas y las otras 45 son todas más tenues que nuestro Sol.

La búsqueda de paralajes estelares había llevado no sólo a la solución de distancias interestelares, sino al descubrimiento de fenómenos como estrellas binarias, la medición de la velocidad de la luz y a la medición absoluta del brillo de estrellas cercanas. Este método causó grandes dificultades para ser aplicado a la medición de estrellas mucho más alejadas. Partimos de la suposición de que las estrellas se encuentran distribuidas aleatoria y uniformemente en el espacio. Sin embargo, hoy sabemos que nos encontramos en una galaxia en forma de platillo con un tamaño de cientos de miles de veces la distancia a Alpha-Centauri. Los primeros pasos que llevaban a tal conclusión ya se habían dado incluso antes de la medición de la paralaje por parte de Henderson. Pero eso lo veremos en el próximo artículo.

Los dejo con un mapa de las estrellas más cercanas a nuestro sistema solar. En esta imagen, las estrellas rojas son mucho más tenues que el Sol siguiendo en orden de brillo absoluto las naranjas, luego las amarillas (con brillo comparable al Sol) y finalmente las blancas (con brillo mucho mayor a nuestro Sol)

Mapa de estrellas más cercanas al sistema solar

1. Recordemos que él propuso el modelo heliocéntrico en Grecia [↩]
2. pues 2,512 * 2,512 * 2,512 * 2,512 * 2,512 * = 100 [↩]
3. Los primeros astrónomos le daban nombre propio, como Aldebarán, a las estrellas más representativas. Sin embargo, la gran cantidad de estrellas obligó a nombrarlas de otra forma. El método de Hiparco consiste en darle a una estrella el nombre de la constelación a la que pertenecen antepuesto por una letra griega que, según el orden del alfabeto griego, representa su brillo entre las estrellas de la constelación. Así, Alpha-Tauri es la estrella más brillante de la constelación Tauri seguida en brillo por Beta-Tauri y así sucesivamente. [↩]
4. Vega es la estrella de referencia en el sistema actual. [↩]
5. Sirio es la más brillante, la tercera es Arturo y Procyon es la octava. [↩]
6. Por un lado, debería tener un movimiento con gran componente perpendicular a la línea de visión, y por otro lado, estar lo suficientemente cerca como para que tal movimiento abarque un ángulo de visión mensurable [↩]
7. ¡Y pensar que los astrónomos conocen a la estrella de Barnard como la estrella fugitiva! [↩]
8. En esta serie hablamos de billones como millones de millones. Cuidado al consultar fuentes americanas, que ellos llaman billón a lo que nosotros llamamos mil millones o millardo. [↩]
9. Los 5 segundos de arco que se mueve la estrella de Barnard en seis meses deben separarse del segundo de arco que, por efectos de paralaje, supuestamente debe presentar según nuestras burdas aproximaciones. [↩]
10. Este fenómeno es uno de los más apreciables, produciendo desviaciones anuales de hasta 40 segundos de arco. A pesar de que tal fenómeno complicó mucho más la medida de paralajes, brindó una prueba más del movimiento de la Tierra, pues este fenómeno no se vería si la Tierra estuviese estática con respecto a las estrellas. Asimismo, permitió a Bradley medir la velocidad de la luz en 285.000 km/s, la medida más exacta que se había conseguido hasta ese entonces, con un asombroso error de sólo el 5%. [↩]
11. La constelación Centauri o Centauro sólo es visible desde el hemisferio Sur [↩]
12. Una unidad astronómica, o UA, es la distancia Tierra-Sol. [↩]
13. Recordemos que un valor numérico menor de la magnitud significa más brillo. [↩]

The ¿Qué tan grande es nuestro vecindario? La distancia a las estrellas más cercanas. by César Augusto Nieto, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.