En el artículo anterior de esta serie dedicada más o menos a la Lógica dimos un vistazo necesariamente rápido al álgebra de Circuitos. Me dejé de contar bastantes cosas sobre simplificación de circuitos, diseño, etc, sobre todo por el método de Karnaugh[1] pero creo que no aportaba gran cosa a lo que quería contar. Y en la red se encuentra bastante documentación al respecto para los electricistas en ciernes…
Así que seguiré con la asignatura de Metodología de Segundo de Carrera, impartida por Don José Cuena Bartolomé en el Instituto de Informática (antes de que se convirtiera en Facultad), allá por finales del año 1973 o principios de 1974…
Entonces, tras contar teoría sobre al álgebra de Boole y de su inmediata aplicación a los Circuitos Eléctricos, Pepe Cuena entró a destripar la Teoría de Conjuntos (ésa que conocíamos malamente del Bachillerato, con sus diagramas de Venn y todo eso), pero con una orientación bastante diferente de la que habíamos visto, con una orientación muy… lógica, si se me permite la expresión. Enseguida veréis por qué digo esto…
Los conjuntos, definidos de la forma clásica, es decir, todos aquellos grupos de elementos dentro del “Conjunto Universal” que son factibles de agruparse por cualquier criterio, más las operaciones Union (+) e Intersección (·)[2] forman un álgebra de Boole, eso es algo bastante claro. De hecho, fue este conocimiento (al que llegamos tras horas de frustrantes especulaciones, como conté en el primer artículo de la serie) el que nos libró de ser ingresados en un frenopático cuando nos enfrentamos por vez primera con el álgebra de Boole, así que lo dábamos por descontado.
Para los que tengáis un poco oxidados los conjuntos, aquí tenéis un par de ellos para vuestro uso y disfrute, A (azul) y B (rojo), inmersos en un “Conjunto Universal” verde que te quiero verde…
La intersección entre A y B es la parte gris rayada; la unión entre A y B es… lo que no es verde; el complementario de A es lo que le falta para ser el Universal, es decir, lo que no es azul (y el complementario de B, lo que no es rojo), etc, etc. Para fijar ideas, suponer, por ejemplo, que el conjunto A son “los rubios” y el conjunto B, “los que tienen más de cincuenta años“, y rápidamente podéis poner cara y ojos a cada uno de los grupitos que aparecen en el dibujo…
También os acordaréis de que un conjunto puede contener a otro. Por ejemplo, el conjunto de los europeos contiene al conjunto de los españoles, y a su vez el conjunto de los españoles está contenido en el conjunto de los europeos, y decimos que “los españoles” son un subconjunto de “los europeos”… Hasta aquí no creo que haya descubierto nada nuevo.
Entremos, pues, en materia:
.
Es evidente que, lidiando con conjuntos:
1- Las dos operaciones (+,·, es decir, Unión e Intersección) son conmutativas.
2- Existe un elemento neutro para cada operación: el Conjunto Vacío, o 0, para la unión (+) y el Conjunto Universal, o 1, para la intersección (·).
3- Ambas operaciones cumplen la propiedad distributiva respecto de la otra ( A·(B+C) = A·B+A·C; y A+(B·C) = (A+B)·(A+C) ).
4- Todo Conjunto A tiene su complementario A’ tal que A+A’=1 y A·A’=0, es decir, el Conjunto A’ es el Universal menos el propio conjunto A.
Así que no queda la menor duda de que los conjuntos, con la Unión y la Intersección, forman un álgebra de Boole.
.
En teoría de conjuntos, una cierta información aplicada a un cierto conjunto permite determinar un subconjunto de él. Por ejemplo, si tenemos el conjunto de todas las ovejas de un rebaño, aplicando una cierta información, un cierto atributo de ellas (el de ser negras, por ejemplo) define un subconjunto del anterior, el que forman las ovejas negras del rebaño, o sea, aquellas ovejas que, perteneciendo al rebaño, son negras, es decir, aquellas ovejas en las que se cumple que la frase “ser negra” es verdadera.[3]
Como no todas las ovejas del rebaño son negras (o sí, quién sabe, pero en principio esto es irrelevante), se define la relación “Estar contenido en” ( ) por la que denotamos que todos los elementos de un determinado conjunto pertenecen también a otro conjunto de rango superior. Así, el conjunto de las ovejas negras de un rebaño está contenido en el conjunto de todas las ovejas del rebaño. No hay mucha ciencia en esto…
) por la que denotamos que todos los elementos de un determinado conjunto pertenecen también a otro conjunto de rango superior. Así, el conjunto de las ovejas negras de un rebaño está contenido en el conjunto de todas las ovejas del rebaño. No hay mucha ciencia en esto…
Estrictamente, un conjunto A es contenido por uno B ( ) cuando todos los elementos de A están también en B, pero el conjunto B puede tener más elementos que no estén contenidos en A… o no, en cuyo caso A y B serían iguales (
) cuando todos los elementos de A están también en B, pero el conjunto B puede tener más elementos que no estén contenidos en A… o no, en cuyo caso A y B serían iguales ( ). En este caso, tanto A contiene a B como B contiene a A.
). En este caso, tanto A contiene a B como B contiene a A.
Si os acordáis del segundo artículo de la serie (dedicado sobre todo a definir la Forma Normal Disyuntiva), comenzaba explicando en él qué era la relación “ser menor o igual que”:  (que se definía como
(que se definía como  ), y cómo esta relación “menor o igual que” definía en un álgebra de Boole una relación de orden parcial. Pues bien, tratándose de conjuntos, la relación “es contenido por” es equivalente a la relación
), y cómo esta relación “menor o igual que” definía en un álgebra de Boole una relación de orden parcial. Pues bien, tratándose de conjuntos, la relación “es contenido por” es equivalente a la relación  , y, por tanto, es también de orden parcial.
, y, por tanto, es también de orden parcial.
Como consecuencia, sólo queda decir que  es lo mismo que decir que
es lo mismo que decir que 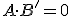 . O sea, en español corriente, que si un conjunto A está contenido en otro conjunto B, entonces la intersección de A con el complementario de B es el conjunto vacío.
. O sea, en español corriente, que si un conjunto A está contenido en otro conjunto B, entonces la intersección de A con el complementario de B es el conjunto vacío.
Y… no pongáis caras raras, que es evidente. Echad una ojeada al siguiente dibujo (que ya salió antes en la serie), y lo entenderéis.
Si A está contenido en B, entonces la intersección de A (la zona azul) con el complementario de B (B’, o sea, la zona gris) es el conjunto vacío, pues no comparten ni un solo elemento… Fácil.
.
Bien, con esto, ya tenemos todo lo que necesitamos para operar con conjuntos. Porque al saber que el álgebra de conjuntos es un álgebra de Boole, sabemos que en la relación de orden se cumple la propiedad transitiva, es decir, si  y
y  , entonces
, entonces  … y eso nos lleva probablemente a entender de una forma nueva[4] las implicaciones de la teoría de conjuntos… Veamos un ejemplo.
… y eso nos lleva probablemente a entender de una forma nueva[4] las implicaciones de la teoría de conjuntos… Veamos un ejemplo.
Supongamos que tenemos una serie de afirmaciones que se suponen ciertas referidas a un cierto entorno, un país, pueblo… o a toda la humanidad, tanto da:
1 – Un hombre que no es feliz no es dueño de sí mismo.
2 – Todo hombre casado tiene responsabilidades.
3 – Todo hombre, o bien está casado o es dueño de sí mismo o ambas cosas.
4 – Ningún hombre con responsabilidades puede pescar todos los días.
¿Qué podemos decir de esta comunidad de vecinos, aplicando lo que sabemos de teoría de conjuntos y del álgebra de Boole?
.
En primer lugar, consideramos como Conjunto Universal el que engloba a todos los hombres de ese entorno al que se refiere el enunciado (país, ciudad, continente…) y definimos luego una serie de conjuntos (todos ellos obviamente contenidos en ese Conjunto Universal) que definimos según la propiedad o propiedades definidas por las frases. En una palabra, cada afirmación está definiendo de forma implícita un subconjunto del Conjunto Universal… y estos subconjuntos son los siguientes (en todos los casos, x representa a un hombre perteneciente al Conjunto Universal):
Conjunto F: x es feliz.
Conjunto D: x es dueño de sí mismo.
Conjunto C: x está casado.
Conjunto R: x tiene responsabilidades.
Conjunto P: x puede pescar todos los días.
Si no supiéramos nada más, si no conociéramos las relaciones entre estos subconjuntos, esto podríamos representarlo, grosso modo, de la siguiente manera (siendo el conjunto H de todos los hombres, el Universal):
Cualquier representación sería factible, claro. Pero es que en realidad sí que tenemos información adicional que nos ayuda a establecer determinadas relaciones entre esos conjuntos… veamos cómo:
1 – Un hombre que no es feliz no es dueño de sí mismo: Esta frase podemos expresarla como que el conjunto de de los “no felices” está contenido en el conjunto de los “no dueños de sí mismos”, y lo representamos como  , pero también como
, pero también como 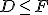 , pues al complementar ambos términos de la ecuación cambia el signo de la relación, o sea, el orden.
, pues al complementar ambos términos de la ecuación cambia el signo de la relación, o sea, el orden.
Traduciendo esta afirmación, 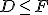 , al español corriente, lo que significa es que el conjunto de los Dueños de sí mismos está contenido en el de los Felices, es decir, los dueños de sí mismos son felices, cosa implícita en la frase del enunciado (de hecho es, estrictamente, la misma frase, pues contiene la misma información), pero que no es, ni mucho menos, tan evidente.
, al español corriente, lo que significa es que el conjunto de los Dueños de sí mismos está contenido en el de los Felices, es decir, los dueños de sí mismos son felices, cosa implícita en la frase del enunciado (de hecho es, estrictamente, la misma frase, pues contiene la misma información), pero que no es, ni mucho menos, tan evidente.
Si os acordáis del segundo artículo de la serie, cuando  entonces
entonces 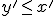 . Pues esa propiedad es la que hemos usado aquí para “dar la vuelta a la tortilla” a la frase.
. Pues esa propiedad es la que hemos usado aquí para “dar la vuelta a la tortilla” a la frase.
Por tanto, de la imagen genérica que teníamos antes, ya podemos decir algo más sobre este par de conjuntos en particular. A continuación, una representación de estos dos conjuntos (subconjuntos del Universal H, en realidad) tal como son uno respecto del otro: F contiene a D.
Sigamos con el resto de enunciados:
2 – Todo hombre casado tiene responsabilidades. Es decir:  , pero también
, pero también  , por la misma razón que antes.
, por la misma razón que antes.
3 – Todo hombre, o bien está casado o es dueño de sí mismo o ambas cosas. En una palabra: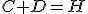 , pues la unión entre los conjuntos C (los casados) y D (los dueños de sí mismos) abarca a todos los hombres. Por lo tanto, siendo H el universal, podemos reescribir la ecuación como
, pues la unión entre los conjuntos C (los casados) y D (los dueños de sí mismos) abarca a todos los hombres. Por lo tanto, siendo H el universal, podemos reescribir la ecuación como 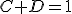 … o
… o 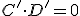 , que, como sabéis, es lo mismo.[5]
, que, como sabéis, es lo mismo.[5]
Sí, es así, es lógico: si C y D cubren conjuntamente todo el Universal, el H, podemos decir que todos los hombres (elementos del conjunto universal) pueden estar en una de estas tres situaciones, y sólo en una: pertenecen a C, pero no a D; pertenecen a D, pero no a C; o bien pertenecen simultáneamente a C y a D. No hay nadie que esté en C’·D’. El siguiente diagrama lo ilustra, siendo la parte marcada en turquesa la intersección de ambos conjuntos C y D.
Luego la intersección de los complementarios de cada conjunto (C’ y D’) es el conjunto vacío. ¿Sí?
Bien, entonces tenemos que 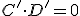 . Si recordamos la definición de la relación de orden parcial “Es Contenido” (
. Si recordamos la definición de la relación de orden parcial “Es Contenido” ( ), sabíamos que
), sabíamos que  . Luego el hecho de que sea
. Luego el hecho de que sea 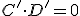 quiere decir, simultáneamente, dos cosas:
quiere decir, simultáneamente, dos cosas:
Una: que  . Dos: que
. Dos: que  .
.
No os hagáis cruces, que es algo evidente: si lo hacemos ahora al revés, vemos que la relación  implica que
implica que 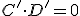 . Pero también la relación
. Pero también la relación  implica que
implica que 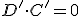 , que es lo mismo. Luego ambas relaciones de inclusión son válidas. Echad un ojo al diagrama de más arriba para entenderlo, si aún os quedan dudas.
, que es lo mismo. Luego ambas relaciones de inclusión son válidas. Echad un ojo al diagrama de más arriba para entenderlo, si aún os quedan dudas.
Por tanto, el tercer enunciado podemos descomponerlo en dos ecuaciones independientes:  y
y  (que, por cierto, son cada una de ellas la complementación de la otra).
(que, por cierto, son cada una de ellas la complementación de la otra).
4 – Ningún hombre con responsabilidades puede pescar todos los días. Es decir:  (los que tienen responsabilidades son un subconjunto de los que no pescan cada día), y también
(los que tienen responsabilidades son un subconjunto de los que no pescan cada día), y también  (los que pescan cada día no tienen responsabilidades).
(los que pescan cada día no tienen responsabilidades).
Si ahora empezamos a ir tomando los enunciados, y aplicando la propiedad transitiva inherente a la relación de orden  , tenemos que:
, tenemos que:
De  (4) y
(4) y  (2), tenemos que
(2), tenemos que  : Los que pescan no están casados.
: Los que pescan no están casados.
De la anterior  y
y  (3), tenemos que
(3), tenemos que  : Los que pescan son dueños de sí mismos.
: Los que pescan son dueños de sí mismos.
De la anterior  y
y 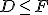 (1), tenemos que
(1), tenemos que  : Los que pescan son felices.
: Los que pescan son felices.
Bueno, ¡tampoco es tanta sorpresa! ![]()
Con todo este conocimiento podríamos representar todos estos conjuntos, por ejemplo, mediante la imagen siguiente:
Donde los que pescan son el grupo amarillo que, ni están casados, ni tienen responsabilidades, pero sí que son dueños de sí mismos y felices; el grupo de los que tienen responsabilidades son todos los casados más el grupito azul claro, que sí son dueños de sí mismos y, por tanto, felices, pero no están casados. El grupo de los felices son todos los dueños de si mismos más la franja roja (están casados, y no son dueños de sí mismos)… en fin, creo que es suficiente.
.
Igual esta ristra de ecuaciones os ha dejado temblando… porque he hecho una serie de conversiones y operaciones que quizá os hayan sorprendido, puesto que estamos hablando de casados, de gente que pesca y de los que son felices o no, y no estamos acostumbrados en absoluto a pensar en conjuntos de personas en términos algebraicos. Y llega entonces el tándem Cuena-Macluskey y se lía a poner ecuación tras ecuación…
Lo que he hecho han sido, en realidad, tres pasos, a saber:
Primero: He convertido los enunciados del problema a ecuaciones algebraicas (de álgebra de Boole, pero algebraicas, al fin).
Segundo: He operado con las ecuaciones, simplificado, etc, aplicando las reglas que conocemos para el álgebra correspondiente hasta llegar a un resultado (o varios parciales, tanto da).
Tercero: He “traducido” el resultado o resultados parciales nuevamente a lenguaje cotidiano: Los que pescan son felices, por ejemplo. Hala.
Y todo esto es una forma de proceder bastante extraña.
.
¡Un momento! ¿Seguro que ésta es una forma extraña de proceder? ¿Seguro? Pongamos otro problema diferente:
“Pepito tiene diez caramelos. Le da tres a su hermana. ¿Cuántos caramelos tiene ahora Pepito?“.
¿Qué hacemos para resolver este singular y dificilísimo problema de Quinto de Carrera?
Primero: Convertimos el enunciado del problema a ecuaciones algebraicas (de álgebra numérica “normal”). Decimos que 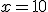 , siendo x el número de caramelos de Pepito antes de la dádiva a su hermana, y que
, siendo x el número de caramelos de Pepito antes de la dádiva a su hermana, y que  , siendo y el número de caramelos que le quedan a Pepito al final y 3, los caramelos que intervienen en la transacción.
, siendo y el número de caramelos que le quedan a Pepito al final y 3, los caramelos que intervienen en la transacción.
Segundo: Operamos con las ecuaciones, simplificando, etc, hasta llegar a un resultado (o varios parciales, tanto da). Aquí, diremos que  . El resultado final buscado es
. El resultado final buscado es  .
.
Tercero: Traducimos el resultado nuevamente a lenguaje cotidiano. Los caramelos que le quedan a Pepito son 7. Hala.
Luego… ¿Qué he hecho yo en el problema de los felices y los casados que no pescan que sea distinto a lo que hacemos normalmente para resolver problemas de cualquier tipo…? Nada. Nada de nada. Únicamente he usado álgebra de Boole en lugar de la “normal”, pero el método utilizado es ni más ni menos que el de toda la vida.
Espero que esta diatriba os haya tranquilizado. Un poco, al menos.
.
Llegados a este punto en el que ya no estamos seguros de que si somos felices es porque pescamos o que si nos casamos es porque no sabemos lo que hacemos, vamos a hablar de las ecuaciones booleanas y las cosas que les pasan que son de utilidad para nosotros.
En primer lugar, cualquier ecuación puede reducirse a una equivalente en que el segundo miembro es nulo.[6] Así,  se reduce simplemente a
se reduce simplemente a  , es obvio, pero ¿qué hacemos con la igualdad,
, es obvio, pero ¿qué hacemos con la igualdad,  ?
?
Pues  es, simultáneamente,
es, simultáneamente,  y
y  . La primera da origen a que
. La primera da origen a que  , mientras que la segunda da origen a que
, mientras que la segunda da origen a que  .
.
Sumamos miembro a miembro, y tenemos que  .
.
O sea, podemos sustituir  por
por  .
.
Además, y como acabamos de observar, podemos reducir cualquier sistema de ecuaciones booleanas a un única ecuación (lo acabamos de hacer, de hecho, en el ejemplo). Si tenemos un par de ecuaciones del tipo  y
y  (como acabamos de ver, toda ecuación puede reducirse a una igualdad con el segundo miembro igual a cero), podemos concluir que
(como acabamos de ver, toda ecuación puede reducirse a una igualdad con el segundo miembro igual a cero), podemos concluir que 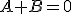 .
.
Por si quedan dudas, tomamos la primera ecuación,  , y sumamos la identidad
, y sumamos la identidad  a cada miembro, lo que nos deja
a cada miembro, lo que nos deja  . Pero B es cero, así que
. Pero B es cero, así que 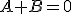 .
.
Por cierto, el sistema es dual, como casi todo en álgebra de Boole: si las ecuaciones fueran  y
y  , entonces podríamos reducirlas a
, entonces podríamos reducirlas a  .
.
Este procedimiento puede generalizarse para cualquier número de ecuaciones, por lo que es evidente que efectivamente es posible reducir cualquier sistema de ecuaciones booleanas a una única ecuación.
Lo que sí puede ocurrir es que un sistema de ecuaciones booleanas sea inconsistente, es decir, que no haya ningún valor posible de sus variables que cumpla todas las restricciones. Esto se puede ver fácilmente al reducir el sistema de ecuaciones original a una sola ecuación y luego aplicar reducciones… por ejemplo, el sistema de estas tres ecuaciones es inconsistente:  ;
;  ;
;  . No voy a decir por qué, para no estropearos el placer de descubrirlo vosotros mismos…
. No voy a decir por qué, para no estropearos el placer de descubrirlo vosotros mismos…
Y si os quedáis con ganitas de más, intentad demostrar si es inconsistente o no el sistema de tres ecuaciones booleanas siguiente:  ;
;  ;
; 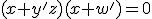 .
.
.
Veamos ahora un ejemplo muy característico, en forma de acertijo de tipo de los que podéis encontrar en los dominicales, debajo del crucigrama y al lado del Sudoku. Dice así:
“Del mítico reino de Thule no se sabe nada… ha estado sumido en la bruma del misterio años y años. Y más años. De hecho, sólo se sabe que su princesa Sigrid era el gran amor (platónico, desde luego) del Capitán Trueno cuyos tebeos[7] tanto leí en mi infancia…
“Pero cuatro thulianos, de turismo en un barco, naufragan frente a las costas de Galicia y, antes de perecer ahogados, dan alguna información sobre el reino de Thule. Esto es lo que cuentan:
“El náufrago número 1 dice que “En el reino de Thule todo el mundo que lleva pluma roja, o está casado o tiene perro o ambas cosas”, y a continuación expira con expresión beatífica.
“El náufrago número 2 asegura que “En el reino de Thule no hay ningún casado que no lleve pluma roja, a menos que sea brujo”, e inmediatamente fallece plácidamente.
“El náufrago número 3 afirma que “Todos los thulianos propietarios de perro que llevan pluma roja están casados”, y muere tranquilamente al instante.
“Por fin, el náufrago número 4, entre estertores, asevera que “No hay brujos en Thule”, y exhala su último suspiro con una sonrisa en su faz.
“¿Qué información nos han dado, en realidad, los cuatro náufragos?”
¿?
No, no me preguntéis por qué razón cuatro honrados y felices ciudadanos del mismísimo y misterioso reino de Thule, en su última hora, dan una información tan idiota. Es lo que tienen los acertijos booleanos…
Vamos con las ecuaciones que descifran los cuatro mensajes, teniendo en cuenta que los conjuntos básicos que aparecen en las declaraciones de los thulianos son:
R: x lleva una pluma roja.
P: x es propietario de un perro.
C: x está casado.
B: x es brujo.
1 – En el reino de Thule todo el mundo que lleva pluma roja, o está casado o tiene perro o ambas cosas, que se representa como  , o sea,
, o sea,  , o sea,
, o sea,  (por la Ley de De Morgan).
(por la Ley de De Morgan).
2 – En el reino de Thule no hay ningún casado que no lleve pluma roja, a menos que sea brujo, lo que se representa como  , es decir,
, es decir,  .
.
3 – Todos los thulianos propietarios de perro que llevan pluma roja están casados, que se representa como  , o lo que es lo mismo,
, o lo que es lo mismo,  .
.
4 – No hay brujos en Thule, que se representa (y ésta sí que es fácil) como  .
.
.
Espero que, hasta aquí, no haya habido problema para entender de dónde salen estas ecuaciones.
Ahora sumamos todos los primeros miembros y los segundos, que obviamente darán 0, y tenemos que: 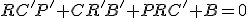 .
.
Ahora se trata de simplificar un poco, a ver qué sale. Reordenando:
![RC'P'+[B+B'R'C]+RC'P=0](https://eltamiz.com/elcedazo/wp-content/cache/tex_20f986070b1062c3e69451c87fa83d06.png)
Ahora, los dos términos centrales ![[B+B'R'C]](https://eltamiz.com/elcedazo/wp-content/cache/tex_159f7ea0ea6855cb84a4c11ff16d7c54.png) podemos sustituirlos por
podemos sustituirlos por  , dado que sabemos que
, dado que sabemos que  y por consiguiente
y por consiguiente  y entonces
y entonces ![[B+B'R'C]=(B+R'C)](https://eltamiz.com/elcedazo/wp-content/cache/tex_575396b237dc633d2bbebe76bf782695.png) . Por tanto, reordenando, queda:
. Por tanto, reordenando, queda:
 ; sacando factor común (por la propiedad distributiva)
; sacando factor común (por la propiedad distributiva) 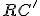 , queda:
, queda:
 , y como
, y como  , queda finalmente:
, queda finalmente:
 .
.
Ahora, en base a los términos de la ecuación, e igualando a cero cada uno de ellos (todos ellos son cero; si no, recordad, no podrían sumar cero)[8] calculamos las relaciones “contenido por” ( ). Como
). Como  , podemos inferir que:
, podemos inferir que:
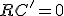 , luego
, luego  ; por otra parte
; por otra parte 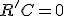 , luego
, luego  ; y por fin,
; y por fin,  .
.
De las dos primeras deducimos que C contiene a R, pero también que R contiene a C… ergo  . Así que podemos por fin informar a nuestros superiores que:
. Así que podemos por fin informar a nuestros superiores que:
 , es decir, traduciendo de nuevo al lenguaje cotidiano, todos los casados de Thule y sólo los casados llevan pluma roja, y
, es decir, traduciendo de nuevo al lenguaje cotidiano, todos los casados de Thule y sólo los casados llevan pluma roja, y
 , o sea, no hay brujos en Thule. Ésta es, en definitiva, la información obtenida de los cuatro náufragos.
, o sea, no hay brujos en Thule. Ésta es, en definitiva, la información obtenida de los cuatro náufragos.
Supongo que os habéis dado cuenta de que, dado que una de las premisas es que “no hay Brujos en Thule“, es decir,  , bien podía haber eliminado de antemano esa B de las ecuaciones donde aparece sumando, puesto que vale 0… Sí. Podía haberlo hecho, pero si no lo he eliminado ha sido para realizar la demostración en su caso general. En cualquier caso, podéis rehacer, si queréis, el razonamiento eliminando donde proceda ese B que es 0… y os dará exactamente lo mismo. Al menos, debería dar lo mismo.
, bien podía haber eliminado de antemano esa B de las ecuaciones donde aparece sumando, puesto que vale 0… Sí. Podía haberlo hecho, pero si no lo he eliminado ha sido para realizar la demostración en su caso general. En cualquier caso, podéis rehacer, si queréis, el razonamiento eliminando donde proceda ese B que es 0… y os dará exactamente lo mismo. Al menos, debería dar lo mismo.
.
¿Dolor de cabeza? Psé, tampoco es para tanto, de veras. Si os han quedado ganas de más, ahí va un clásico, que no voy a resolver para no estropear el disfrute:
“En un tren viajan tres empleados de ferrocarriles, el jefe de tren, el maquinista y el camarero, de nombres White, Black y Brown, aunque no necesariamente en ese orden, y viajan también tres viajeros que tienen los mismos nombres, White, Black y Brown. Tenemos además los siguientes datos sobre ellos:
“El viajero Black vive en Washington, pero el camarero vive a mitad de camino entre Washington y New York, mientras que el viajero que se llama igual que el camarero vive en New York. El viajero Brown gana doscientos mil dólares justos al año. El empleado de ferrocarriles de nombre White gana siempre al ajedrez al jefe del tren. Uno de los viajeros es vecino del camarero y gana exactamente, hasta el último céntimo, el triple que él.
Y la pregunta es… ¿Cómo se llama el maquinista?”[9]
.
Hasta aquí esta visión de la teoría de conjuntos con un poco de… lógica. En el próximo episodio de la serie entraré, de una santa vez, de la mano de Don José, en el Cálculo Proposicional. Pero… antes simplista que incomprensible, ¡eh! Hasta la próxima.
Disfrutad de la vida, mientras podáis.
- Se suponía en aquellos lejanos tiempos que igual nos tendríamos que dedicar al diseño de hardware, así que se contaban todas estas cosas; en la realidad, el 95% o más de nosotros nos dedicamos al software. [↩]
- Aviso: Usaré siempre + y · en vez de
 y
y  . [↩]
. [↩] - Ovejas negras: la intersección entre “las ovejas” y “las cosas que son negras”… o algo así. [↩]
- Bueno, igual no. [↩]
- Aplicando la Ley de De Morgan. [↩]
- No sólo en las ecuaciones booleanas; es obvio que en las algebraicas “normales” también. [↩]
- Aún no sabíamos que se llamaban comics. [↩]
- En álgebra de Boole, para que una suma de términos a+b+…c dé 0 es necesario que cada uno de los sumandos, a, b…c, sea 0, es decir, el conjunto vacío si hablamos de Conjuntos. Obviamente esto no es ni mucho menos cierto en álgebra numérica “normal”, pero sí en la de Boole. [↩]
- Aunque yo conozco el acertijo desde hace más de cuarenta años, incluso mucho antes de estudiar lógica, es relativamente fácil encontrar el acertijo y su solución en la Red. No lo hagáis: con un poquito de paciencia se resuelve bien, y es muy agradecido de resolver… ¡y siempre podéis torturar a algún amigo o pariente con el dichoso maquinista!
 [↩]
[↩]

The Eso que llamamos Lógica (IV) El álgebra de Conjuntos, revisitada. by , unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.











{ 4 } Comentarios
Me ha gustado mucho este artículo práctico sobre lógica.
Ojalá tuviese más tiempo libre para poder empaparme de todos los conocimientos necesarios para resolverlos por mí mismo.
Saludos.
Hola Mac, Creo que tienes un pequeño fallo en la nota 2: creo que has cambiado el orden de los símbolos unión e intersección. Un saludo
Caramba, Ril, qué buena vista… Cómo se nota que aún sois jóvenes
Corregido. ¡Gracias!
Gran artículo Mac!
Saludos
Escribe un comentario