Como siempre me pasa, he disfrutado como un enano leyendo vuestras soluciones al desafío de la semana pasada, la “ametralladora” cualitativa. Creo que la dificultad no estaba demasiado mal calculada, porque la mayor parte de vosotros habéis acertado entre dos y tres de las cinco preguntas –más a menudo tres que dos–, unos cuantos habéis logrado responder correctamente a cuatro de las cinco, y dos de los participantes (si no me he “comido” a nadie, que a veces pasa) habéis respondido correctamente a todas.

El objetivo principal era, desde luego, haceros disfrutar un rato pensando pero, además, mi intención era incluir alguna pregunta más puñetera con la que tal vez alguno aprendiese algo nuevo… veremos, aunque eso depende de los finalistas y ganadora, y si han hecho su trabajo bien al explicar las cosas. Vayamos por partes:

Pregunta 1

La Pregunta 1 era la del trineo: ¿cuál de las tres opciones es mejor, barrer la nieve perpendicularmente al suelo en el sistema de referencia del suelo, hacer lo mismo en el sistema de referencia del trineo o no hacer nada?

La respuesta es que lo mejor era la opción (a), barrer la nieve perpendicularmente al trineo en el sistema de referencia del suelo. La explicación de Argus es breve pero creo que bastante clara:

Lo más eficiente será barrer la nieve en perpendicular en el sistema de referencia del suelo.

Además de quitar nieve de delante que frene al trineo, la estamos empujando en oblicuo hacia atrás en el sistema de referencia trineo. La componente longitudinal de esta fuerza ejercida sobre la nieve, va hacia atrás en el sistema trineo, lo que producirá una cierta reacción hacia adelante.

Es fácil verlo si consideramos que en lugar de nieve estamos apartando grandes rocas de dos en dos, una por la izquierda y otra por la derecha. Lo eficiente es avanzar apartando y empujando las rocas hacia atrás lo máximo posible. Por el contrario, no se debe intentar que acompañen al trineo en su movimiento hacia adelante, lo que equivaldría a apartarlas en perpendicular en el sistema trineo. Eso nos frenaría.

Tal vez las figuras de Paloma lo aclaren aún más:

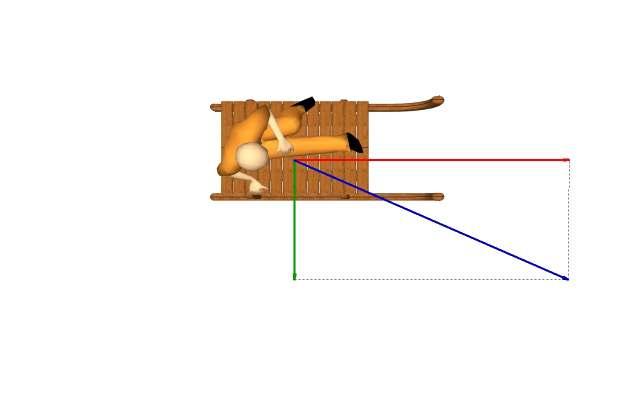
Para la opción a) en el dibujo de abajo puede observarse en rojo la trayectoria del trineo con referencia al suelo, en azul la de la nieve arrojada desde éste, también con referencia al suelo y por último en verde la trayectoria referenciada al trineo que habría que dar a la nieve expulsada para que cumpla éste último requisito de perpendicularidad con referencia al suelo.

Obtenemos así un empuje neto sobre el trineo que sería igual a la masa de la nieve multiplicada por la velocidad a la que la arrojamos y por el coseno del ángulo que forme la trayectoria de expulsión de la nieve con referencia al trineo (verde) con la trayectoria de éste (rojo).

Según se vaya reduciendo el movimiento del trineo debido al rozamiento, éste ángulo con el que tendremos que arrojar la nieve para mantener la perpendicularidad con referencia al suelo se hará cada vez mayor, con lo que el empuje que conseguimos se reduce cada vez más.

Opción a).

Para la opción b) en el dibujo de abajo aparece igualmente en rojo la trayectoria del trineo con referencia al suelo.

Nótese que en éste caso, debido a que la trayectoria de la nieve (en verde) es perpendicular con referencia al trineo, no se obtiene ningún empuje neto sobre éste. La trayectoria azul sería la de la nieve arrojada desde el trineo vista con referencia al suelo.

Opción b).

Pregunta 2

La Pregunta 2 era, en mi opinión, la segunda más difícil de las cinco. Había que decir qué le sucederá al nivel del agua si se fundía un cubito de hielo flotando en una piscina que contuviera una burbuja de aire en primer lugar, y una bola de plomo en el segundo.

La respuesta correcta es que el nivel del agua desciende en el caso del plomo, y desciende un poquitín en el caso de la burbuja de aire; muchos de vosotros habéis considerado que la densidad del aire es tan pequeña que podemos despreciar el peso de la burbuja, algo perfectamente razonable y que he considerado como válido. De modo que, en el caso de la burbuja, tanto “permanece constante” como “desciende ligerísimamente” son respuestas válidas.

La respuesta de Paloma considera despreciable el peso de la burbuja y explica además algo muy interesante – qué sucedería mientras la burbuja sube hacia la superficie si es que estuviera bajo el nivel del agua al fundirse el hielo:

Un bloque de hielo puro (esto es, sólo de agua, sin aire ni ninguna otra sustancia extraña dentro), flota porque la densidad del hielo es menor que la del agua líquida.

Por el principio de Arquímedes la parte sumergida desaloja un volumen equivalente de agua cuyo peso ejerce un empuje sobre el bloque hacia arriba que equilibra a su peso total.

Por ello, cuando el bloque se va licuando el nivel del líquido del recipiente que lo contiene no sube ni baja, ya que entonces el volumen del agua que formaba el bloque se habrá reducido justo al mismo volumen que permanecía sumergido cuando estaba en estado sólido.

Si el mismo bloque contuviese ahora una burbuja de aire, el peso del bloque sería prácticamente el mismo (despreciando el peso del aire), con lo que el volumen sumergido seguiría siendo justo el necesario para elevar dicho peso, es decir el mismo que sin burbuja. Lo único que varía ahora es que la parte emergida que será mayor, justo en el volumen que tenga la burbuja.

El nivel del agua en el recipiente no variará al final, por el mismo razonamiento de antes, ya que el aire escapará a la atmósfera en cuanto se vea libre. Sin embargo durante el tiempo que tarda la burbuja desde que se desprende del bloque hasta que llega a la superficie, el nivel del líquido subirá al volumen correspondiente a la burbuja, volviendo a bajar después al nivel inicial. Por ello este experimento hará que rebose el recipiente momentáneamente si lo hubiésemos llenado hasta el borde.

En el caso de que contuviese un material más pesado que el agua, como el plomo, el bloque sí se sumergirá más, para que el peso de agua correspondiente al volumen desalojado compense la diferencia de densidad de la bola de plomo respecto de su volumen de hielo.

Según se vaya licuando el hielo el porcentaje de volumen de hielo emergente se hará cada vez más pequeño, aumentando progresivamente el nivel del agua del recipiente, hasta que llegue un momento en que sucedan una de estas dos cosas: 1: El plomo se desprende del hielo y cae al fondo mientras que el hielo, liberado abruptamente de su peso, disminuye su porcentaje de volumen sumergido, bajando el nivel del agua del recipiente.

2: La densidad conjunta del bloque de hielo con el plomo supera la densidad del agua líquida, con lo que cae al fondo y a partir de ahora, mientras se funde el resto del hielo el nivel del agua del recipiente disminuye progresivamente al elevarse la densidad de ésta por pasar el hielo sumergido al estado líquido.

Por su parte, Argus nos explica, con unos dibujos de una calidad inefable, que rivalizan con los míos en la pizarra todos los días, cómo razonar si tenemos en cuenta el peso de la burbuja, por pequeño que sea, además de explicarnos qué sucede en el caso del alcohol y cubitos que no flotan:

En ambos casos el nivel del agua desciende.

El conjunto hielo-aire igual que el conjunto hielo-plomo, en caso de estar flotando, pesan igual que el volumen de agua desalojada. Esto es así por Arquímedes. Bueno, en realidad es así por otras razones, pero fue Arquímedes quien nos puso esas razones delante de las narices.

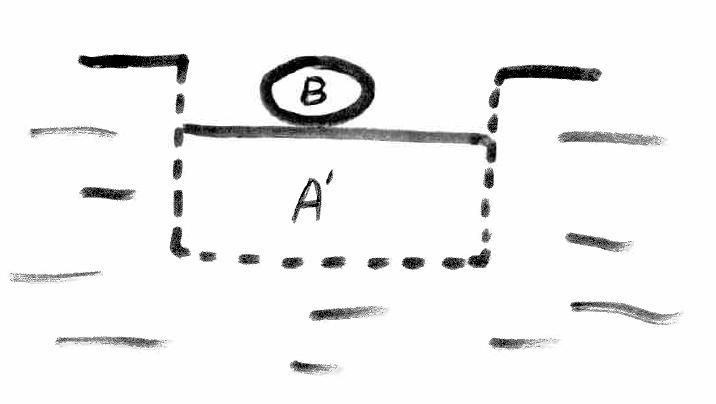
En los dibujos, A es el hielo, B es aire o plomo o lo que sea y A’ B’ son las cantidades de agua que pesan igual que A y B:

Si B es aire, el volumen B’ será casi imperceptible [1], pero no nulo. Podríamos decir que el nivel se mantiene prácticamente igual, aunque matemáticamente desciende.

Si B es más denso que el agua no se llegará tampoco a llenar el volumen de agua desalojada en un principio y el nivel de agua descenderá:

[1]- Recuerdo que estamos hablando de una piscina con agua, donde el hielo con aire va a estar flotando. Hay otros ejemplos donde el descenso de nivel no es en absoluto inapreciable y la cosa cambia mucho: Una columna de cubitos de hielo sumergidos en alcohol en un vaso de tubo no flotan ni con aire dentro. En ese caso el descenso del nivel de alcohol una vez fundido el hielo sí es bastante apreciable. Esto lo saben en cualquier bar donde pongan los cubatas con el hueco del hielo hacia abajo y no hacia arriba, o sea, en todos a los que yo he ido. En caso de que el conjunto hielo-plomo no flotase, igualmente descendería el nivel de agua, pues el hielo al fundirse daría lugar a un volumen de agua menor.

Pregunta 3

La Pregunta 3 era probablemente la más difícil de todas: dos vasos comunicantes con formas distintas y temperatura (y por tanto densidad) cambiante… ¿hacia dónde fluye el agua si se calienta A o se calienta B? Muy poquitos de vosotros habéis logrado responder correctamente, pero es que se las trae… casi todo el mundo responde que no pasa nada, o que en un caso el agua fluye de A a B y en el otro de B a A.

La respuesta correcta, sin embargo, es que el agua fluye de B hacia A en ambos casos. En palabras de Javier,

Si los recipientes tuvieran las paredes rectas, podemos razonar que no habrá flujo de agua de un recipiente al otro. En el fondo del recipiente habrá una presión hidrostática que vale igual al peso de la columna de agua que hay por encima. Si calentamos el líquido, aunque suba la altura de la columna por la dilatación, no cambia la masa de agua que hay encima (ni el peso por descontado) por cada unidad de superficie. Estamos suponiendo que las dimensiones del recipiente no cambian, ya sea porque el material tiene un coeficiente de dilatación despreciable o porque lo estamos refrigerando para mantener su temperatura constante.

a) Si calentamos el agua del recipiente A, que se ensancha, la subida de nivel será menor que la que habría en el caso de un recipiente recto. Por lo tanto habrá una disminución de la presión hidrostática en el fondo y habrá un flujo de agua desde el recipiente B.

b) Si calentamos el agua del recipiente B, que se estrecha, la subida de nivel será mayor que la que habría en el caso de un recipiente recto. Por lo tanto habrá un aumento de la presión hidrostática en el fondo y habrá un flujo de agua hacia el recipiente A.

En cualquier caso, hay un flujo de agua del recipiente B al A.

Paloma nos da una respuesta que utiliza los mismos conceptos, pero la incluyo por si a alguno le ayuda a encender la bombilla por ser más detallada:

Para simplificar el problema, vamos a suponer primero que el recipiente que estamos calentando está formado por un cilindro y no por troncos de cono como A ó B.

Al calentarse el agua de un recipiente cilíndrico, ésta se expande, y el nivel en el recipiente subirá siempre proporcionalmente a la temperatura, esto es, a incrementos iguales de temperatura les corresponderán incrementos iguales de nivel para todo el intervalo comprendido entre las temperaturas de fusión y de ebullición a presión atmosférica constante.

Pero ¿qué le sucede a la presión de agua en el fondo del recipiente cilíndrico cuando su nivel sube por efecto de la dilatación térmica? Como la presión sobre una superficie en el interior de un líquido es equivalente al peso de la columna de líquido de sección igual a dicha superficie y altura igual a la distancia hasta la superficie libre, dicha columna contendrá siempre la misma masa de líquido, por lo que la presión no variará en función de la temperatura en este caso.

Esto no sucederá así en un recipiente cuya sección aumente (caso A) o disminuya (caso B). En estos dos casos, los incrementos de nivel serán cada vez menores en un caso y cada vez mayores en el otro según vayamos subiendo en el rango de temperatura.

Así, la presión en el fondo del recipiente disminuirá con el aumento de temperatura en el caso A, mientras que aumentará en el caso B.

Podemos por lo tanto contestar ahora a las dos preguntas:

En el caso a), al disminuir la presión en A, el agua fluirá desde el recipiente B hacia el A por el tubo de comunicación, mientras que en el caso b), también fluirá el agua desde B hacia A, pero esta vez por haber aumentado la presión en B. Se da así la paradoja que en el caso a) el nivel en A sube, mientras que baja el de B. En el caso b) suben los niveles de ambos recipientes, el de A por la entrada por el tubo de comunicación y el de B por dilatación térmica, quedando en equilibrio el del recipiente B más alto que el de A, al contener agua más caliente y por lo tanto menos densa.

Si el recipiente que calentásemos fuese cilíndrico (o de sección constante), el nivel subiría sobre el del recipiente más frío sin que se produjese ninguna circulación de líquido por el tubo de comunicación que los igualase, como sucede normalmente con líquidos de densidad homogénea. (sí se producirían en el vaso comunicante pequeñas corrientes de torbellino que acabarían por mezclar el líquido e igualar los niveles a la larga).

Pregunta 4

La Pregunta 4, sin embargo, os ha resultado más fácil de lo que pensaba – en este caso lo bueno es que era posible realizar el experimento en vivo, para comprobar lo que pasaba.

La respuesta correcta es que las monedas terminan así:

Y la pega más común que suele poner la gente es que, si la moneda ha girado 180°, ¿por qué no termina invertida como en la segunda figura? Pero, mejor que yo, lo explicáis vosotros.

En palabras de Argus,

El error más común en este tipo de problemas es pensar que un cambio de posición de 180o de una moneda respecto de la otra, produce una rotación igualmente de 180o. Esto sería correcto si en lugar de rodar hubiese girado respecto al centro de la moneda fija, pero hay que tener en cuenta que eso produciría deslizamiento en el punto de contacto.

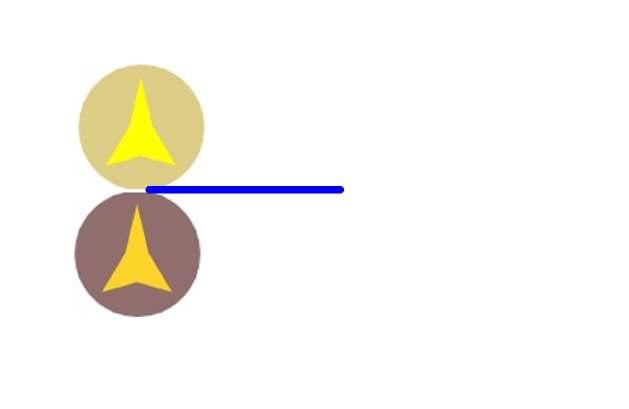
Para ver por qué no es así, nos puede ayudar si imaginamos que son dos relojes. En la posición inicial, las 6 del reloj de arriba toca con las 12 del reloj de abajo.

Haciendo rodar el reloj de arriba un poco, sin deslizamiento, veremos que la siguiente coincidencia serán las 5 del reloj de arriba con la 1 del reloj de abajo. ¿Qué está sucediendo? Pues que cuando el punto de contacto en el reloj de abajo es una hora más, el punto de contacto en el reloj de arriba es una hora menos.

En la posición final, el punto de contacto en el reloj fijo ha aumentado en 6 horas, por tanto el punto de contacto del reloj móvil ha disminuido en otras 6 horas y vuelven a estar en contacto las 6 con las 12 y nunca las 6 con las 6.

Dicho más formalmente, el ángulo de giro de la moneda móvil sobre sí misma es el doble que el ángulo entre los puntos de contacto inicial y final en la moneda fija. Cuando el punto de contacto en la moneda fija se sitúa a 180° del punto inicial, el ángulo de giro de la moneda móvil habrá sido del doble, es decir, 360°.

Por si a alguien le queda alguna duda, Paloma nos regala la vista, una vez más, con dibujos clarificadores:

La respuesta incorrecta es la segunda. El error se produce al pensar que si se hace rodar la moneda de arriba una longitud de media circunferencia, ésta habrá dado sólo media vuelta, por lo que quedara boca abajo respecto de su orientación original. Sin embargo se produce un segundo giro de 180 grados y del mismo signo que el anterior, por lo que el resultado correcto es que vuelve a quedar en la misma orientación inicial, tal y como se ve en la primera respuesta. Los siguientes dibujos aclaran cada uno de los giros.

Representación del recorrido que efectuará la moneda superior, en azul, por el canto de la moneda inferior.

Vista del mismo recorrido estirado, en azul.

Primer giro de 180° a causa del recorrido.

Tras el segundo giro de 180° a causa de volver a curvar el recorrido sobre el canto de la segunda moneda.

Pregunta 5

Finalmente, la Pregunta 5 nos daba un razonamiento incorrecto sobre una bola de acero girando alrededor de un clavo, con el hilo enrollándose y la bola moviéndose cada vez más deprisa de modo que no se conservaba la energía. ¿Dónde estaba el error en el razonamiento?

La respuesta correcta es que la bola se mueve con la misma rapidez todo el tiempo; gira más deprisa, pero dado que el radio de giro va disminuyendo, la velocidad angular aumenta, dando la impresión de que la bola “se acelera”. En palabras de Argus,

Efectivamente su energía cinética se conserva porque su velocidad lineal, su celeridad, se mantiene constante. Ahora bien, cada vez el radio de giro es menor, por tanto la longitud de la circunferencia descrita es también menor y a igual velocidad lineal, completa las vueltas más rápido.

Esto me recuerda a los profesores del colegio en el recreo haciendo girar el silbato alrededor de una cadenilla que se iba enrollando en el dedo. Hasta muchos años más tarde no comprendí por qué diablos el dichoso silbato aceleraba sin motor y sin hélices.

Sin embargo, nadie (ni siquiera ganador y finalistas) ha mencionado algo importante y curioso, que os planteo para ver si alguien puede resolverlo en comentarios –eso sí, esta vez hace falta conocer conceptos como el momento angular–. Efectivamente, la energía se conserva y la velocidad lineal también: la bola siempre va igual de rápido. Sin embargo, si la velocidad lineal es constante y el radio de giro disminuye, lo que no se conserva es el momento angular, a pesar de que la fuerza que sufre es una fuerza central, hacia el clavo… ¿dónde está el error en el razonamiento que acabo de hacer y cómo se explica lo que sucede?

Respecto a finalistas y ganador, cuyas soluciones completas dejo más abajo en PDF: los dos finalistas son Argus y Javier. Javier ha explicado muy bien varias respuestas y ha acertado en cuatro de las cinco, y Argus ha contestado bien a todas y explicado las cosas estupendamente bien; también ha contestado correctamente a todas las preguntas Paloma (Argus y ella han sido los únicos salvo que, como decía antes, me haya saltado algo), pero sus dibujos y explicaciones son tan maravillosos que Paloma es la ganadora del desafío de hoy (aunque Argus ha estado a un tris). ¡Enhorabuena a los tres!

Como siempre, dejo aquí las soluciones completas de finalistas ganadora: soluciones de Javier, soluciones de Paloma, soluciones de Argus. Y, también como siempre, los finalistas y ganadora podéis contar con el número de septiembre en el correo –en cuanto lo tengamos listo– para que podáis guardar este pobre honor.

Espero que hayáis disfrutado y ¡hasta el próximo desafío en noviembre!