En el artículo anterior de esta serie sobre Música y Ciencia prometíamos una orientación objetiva fundada en argumentos menos trillados que los de todos los días en la discusión alrededor del atonalismo. Puede parecer sorprendente iniciar un tema así a partir del círculo de quintas, conocido por todos los músicos como el símbolo por antonomasia representativo de las tonalidades. ¿Es que todavía quedará algo por decir acerca de eso? Pues sí, queda mucho por decir y – como veremos – directamente vinculado al atonalismo en general y al dodecafonismo en particular.
Cuando Pitágoras hizo su célebre enunciado: “Cualquier intervalo puede expresarse como una combinación de un número mayor o menor de quintas justas” estableció el cimiento de toda la música occidental durante los próximos 2500 años a partir de aquel momento. Ése sería el gran legado musical de la antigua Grecia, un tema desarrollado en el artículo más largo de toda la serie a causa de la importancia histórica. En efecto, el enunciado pitagórico permite deducir la escala diatónica calculando 7 quintas justas consecutivas partiendo de un cierto sonido original, lo cual se obtiene multiplicando su frecuencia por 3/2 – es decir, 1,5 – siete veces. Luego, Pitágoras y Aristógenes desarrollarían el cálculo hasta la cantidad de 12 quintas justas – multiplicando la frecuencia original por 3/2 doce veces –, lo cual equivalía a calcular siete octavas consecutivas sobre el mismo sonido original (es decir, multiplicar su frecuencia por 2 siete veces). De este cálculo derivaría el sistema de 12 tonalidades que hoy conocemos.
Pero he aquí, según ya vimos, que 12 quintas justas no cuadran con 7 octavas, y Pitágoras descubrió una pequeñísima diferencia que denominó “coma”. El valor de la coma es de 1,0136433, es decir, la diferencia entre las frecuencias de dos sonidos separados por una coma es de un 1,36%, diferencia pequeña, pero que es perfectamente audible, como se puede escuchar en el ejemplo siguiente, donde se escuchará un cierto sonido, en concreto un La con su afinación habitual de 440 Hz, y a continuación otro sonido separado del anterior una coma, es decir, de unos 446 Hz.
Clip de audio: Es necesario tener Adobe Flash Player (versión 9 o superior) para reproducir este clip de audio. Descargue la versión más reciente aquí. También necesita tener activado Javascript en su navegador.
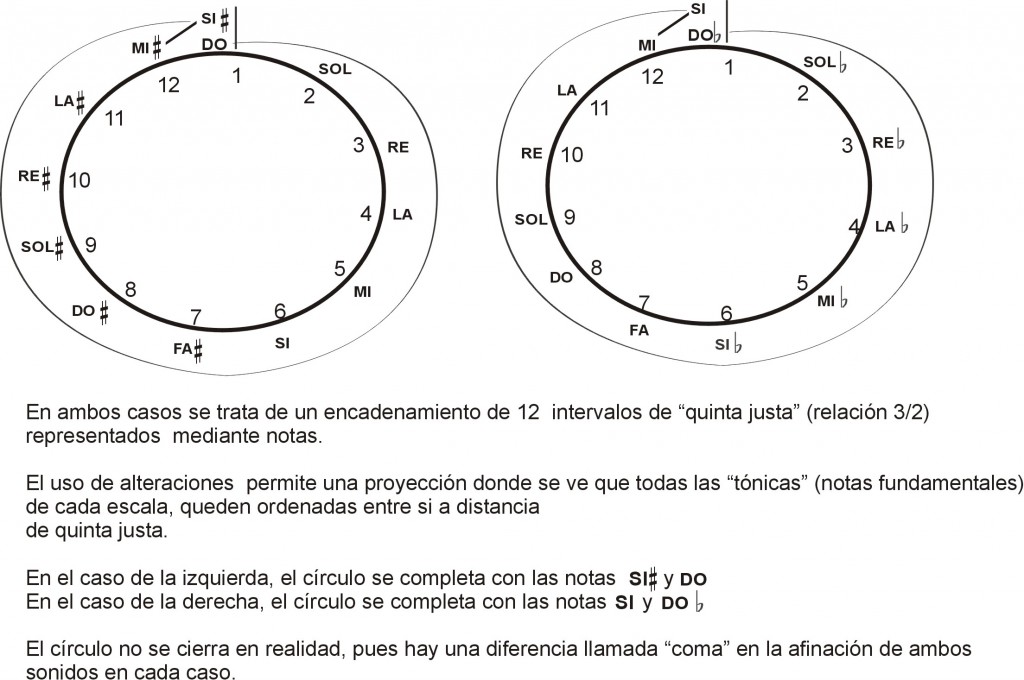
El descubrimiento de la coma sería la causa de diversos problemas, ya en aquella época, pero harían crisis varios siglos después, cuando el sistema de las tonalidades habría de terminar sustituyendo al sistema modal de los griegos. En el año 1679 el teórico y compositor ruso Nikolai Diletski escribía el que se considera primer tratado de composición de la historia, y allí aparece por primera vez el diseño del “Círculo de Quintas”, que es un diagrama que intenta visualizar el problema de la coma en el cálculo de 12 quintas justas consecutivas:
Pero el círculo de la figura no supera las 12 quintas, y no sabemos lo que sucede más allá de ese límite. Esto ya es más interesante.
¿Qué sucedería si comenzásemos a calcular quintas justas indefinidamente en dos sentidos: en uno, hacia los sostenidos, y en otro, hacia los bemoles?
Cierto día, tras releer el antes citado artículo, Macluskey se hizo esta pregunta suponiendo una afinación (frecuencia) de 1.000 Hz para el DO (es una afinación ficticia, pues en realidad – como lo hiciéramos notar varias veces – ningún DO en ninguna afinación usual tiene exactamente esa frecuencia, pero un número redondo facilita comprender los ejemplos) y he aquí el resultado que obtuvo:
Este resultado no deja de ser tan sorprendente como inquietante, pues muestra nada menos que la imposibilidad de darle nombre a todas las notas a partir de cierto límite. Y, como si esto fuese poco, empiezan a sumarse más comas, sin explicación aparente, siendo que la predicción de Pitágoras era que al cabo de 7 octavas se sumaba sólo una coma.
Intrigado, me hizo una consulta al respecto suponiendo que yo hallaría alguna explicación recurriendo a la teoría de la música. Así nació este nuevo capítulo de la serie sobre Música y Ciencia.
Un resumen del problema, para comenzar
A medida que van sumándose las comas pueden desaparecer los nombres de algunas notas, en efecto, pero no desaparecen los sonidos. Para que no desaparezcan los nombres habría que usar nuevas “alteraciones” para los únicos 7 nombres existentes de las notas, como vimos en el artículo dedicado al alfabeto de la Música. Para eso existe el doble bemol (bb), el triple si hiciera falta (bbb), y así hasta que se quiera. También hay dobles sostenidos (el símbolo del doble sostenido es x), triples (x#), cuádruples (xx), quíntuples (xx#) y así en adelante. Así que habría que usar esos símbolos para que cada nota tuviese un nombre. Esto es, para empezar, una complicación de la escritura, pero además, como veremos en seguida, poco contribuye a una visión más clara de este asunto.
Cuando se llega al FAb de 1231,785 Hz y se comprueba que no está la nota SI y aparecen 2 comas, lo que ha sucedido es que el LA que sigue en la proyección no es un LA sino un SIbb para poder formar la relación 3/2, a la que luego seguiría un MIbb, que no es lo mismo que RE, etc. O sea: caímos en el problema ya planteado en el artículo tantas veces mencionado, es decir, LA# no es lo mismo que SIb y, en este caso, ahora ocurre que SIbb no es lo mismo que LA.
Entonces, si recordamos que hay una diferencia de una coma entre LA# y SIb, ahora no podría ocurrir otra cosa que aparecer 2 comas, porque el bemol es “doble”. Lo mismo seguirá ocurriendo de ahí en adelante: 2 comas de diferencia para cada nuevo sonido en relación 3/2. Y, si no hay otra forma de nombrar individualmente todas esas nuevas notas que van surgiendo, parecería que el problema estaría resuelto. Pero ¿lo estará realmente?
Observemos ahora esto otro: la nota innombrada FA + 2 comas (1.369,964 Hz en el cuadro) debería ser MI#+2 comas – para poder contar 5 notas desde el LA# y decir que es una “quinta” – pero… aunque pongamos bien el nombre de la nota, después tendremos el problema de que en vez de DO habrá que indicar SI#+2 comas (en vez de DO+2 comas), FAx (doble sostenido)+2 comas en vez de SOL… etc. , con lo cual no habríamos adelantado mucho camino… y lo que es peor, sigue costando entender cómo funciona todo esto.
Los músicos cortan por lo sano en estos casos: rarísima vez usan una triple alteración (DO x#, por ejemplo) y escriben directamente RE#, gracias al uso común que hoy se hace del temperamento igual. Y hacen lo mismo con los bemoles: en vez de RE bbb escriben SI, y listo. A lo sumo se usan alteraciones dobles, pero se puede evitar tener que escribirlas, porque sin duda la famosa raíz 12 de 2 tiene sus ventajas.
Pero tampoco está todo solucionado de esta manera, y… ahora viene lo peor. Si al cabo de 12 quintas (en la 7ª octava) se produce una diferencia de una coma respecto al sonido original de base – tal como descubriera Pitágoras –, entonces al cabo de 24 quintas tendremos 2 comas de diferencia, luego 3 comas al cabo de otras 12 quintas, y así en adelante. ¿Será cierto?
Veamos lo que ocurre tomando esta vez una afinación (igual de ficticia que la anterior) para un Do de 100 Hz:
Pues no, no es como suponíamos, no exactamente. El problema que aquí se ve, llevando la proyección hasta 36 quintas y 21 octavas, es que la diferencia en Hz va en notorio aumento, para cada octava, cada 12 quintas, y, a cada vez, aumenta mucho más que unas pocas comas. Veamos:
Diferencia con la 7ª octava: 174,634 Hz, que representa Una Coma: 
Diferencia con la 14ª octava: 4.5011,246 Hz, que representa Una Coma al cuadrado: 
Diferencia con la 21ª octava: 8.701.244,458 Hz, que representa Una Coma al cubo: 
Generalizando, cada vez que “gira la rueda” se introduce una coma de diferencia con la vuelta anterior, por lo que, respecto de la frecuencia fundamental, esos 100 Hz iniciales, la diferencia acumulada en la vuelta n no es de n comas, sino de una coma^n. Es decir, la diferencia crece exponencialmente, crece más cuantas más vueltas demos en la espiral hasta hacerse eventualmente tan grande como se desee.
Este fenómeno ya había sido descubierto en unos pocos estudios al respecto, donde se ve que la representación gráfica no da un círculo, ni tampoco una espiral homogénea, sino que da una espiral que se abre indefinidamente y la diferencia no se mantiene estable: sigue en aumento cada 12 quintas, y cada vuelta es más abierta que la anterior.
Pero aquí está lo que se me ocurre llamar “la trampa de los músicos”: se acostumbra a ver esto a partir de un “centro natural” (la escala de Do) desde donde parten dos proyecciones “alteradas” en sentidos contrarios, una hacia los sostenidos y otra hacia los bemoles. Usualmente el círculo de quintas no va más allá de las “enarmonías” (SI-DOb por un lado, y SI#-DO por otro lado) y ahí se detiene. Por esta razón es por lo que no se llega a ver lo que muestra la tabla de arriba.
Ahora bien, cualquier músico atento ya habrá advertido que venimos manejando dos círculos (uno que cierra en SI-DOb, y otro en SI#-DO), cuando lo acostumbrado es presentar un solo círculo. Es que existen varios modelos del círculo – como el que se cierra en la enarmonía FA#-SOLb , otro que resuelve el problema cerrándose en el intervalo SOL#-MIb , que es enarmónico de la quinta LAb-MIb, otro más que propone una mitad del círculo en quintas para los sostenidos y la otra mitad en cuartas para los bemoles… – en fin, lo único que revelan todas esas complicaciones es que el razonamiento va dirigido mucho más hacia la escritura de las notas que a los cálculos, que es el inconveniente sobre el que hemos insistido repetidamente.
Además, también tenemos que entre las explicaciones de la teoría musical hay otra verdadera “trampa” para el que quiera entender bien todo esto, y se trata de la teoría de los “tetracordios”.
Esta palabreja (“tetracordio”=cuatro cuerdas) esconde en realidad un error histórico, pero no quiero desviar el tema con ese detalle ahora. Lo único que necesitamos saber es que el círculo de quintas es un diagrama que intentó reducir este otro esquema:
O a la inversa, para los bemoles:
Tratemos de entender este par de jeroglíficos. Los famosos “tetracordios” los podemos identificar en las figuras observando que siempre hay grupos de 4 notas que coinciden entre dos escalas, y donde el segundo de una escala se adopta como primero de la siguiente, si se va hacia los sostenidos, o a la inversa si se va hacia los bemoles, siempre partiendo de la escala “natural”. Pero veamos esto más claro calculando, por ejemplo, cómo resulta la proyección “inversa” de los sostenidos, o sea, la que “baja” por quintas hacia los bemoles, donde las comas no se suman, sino que se restan:
El caso aquí es que “bajando quintas” (al igual que el inverso que se podría calcular “subiendo quintas”) es un método que no se corresponde con la realidad física: todos, absolutamente todos los sonidos forman una secuencia de relaciones armónicas 3/2 cuya frecuencia de partida podría ser en realidad cualquiera (así fuese infinitesimal, teóricamente hablando) y luego se desarrollará en un solo sentido y no en dos.
Se podría empezar con una frecuencia inicial de 0.000000001 Hz, si quisiéramos. Claro, que… ¿qué nombres llevarían esas “notas”? Pues… ninguno; sólo sería posible algo como 1,2,3,4… o parecido. ¿Puedes imaginarlo? Nada de DO-SOL = 3/2, porque entonces, cuando llegamos a la quinta N° 8, ya tenemos problemas para saber cómo se llaman de ahí en adelante las notas medidas en Hz, y ni hablar de lo que pasa llegando a la quinta N° 25 ó a la 36.
Analizando todo esto desde el punto de vista matemático, hay un hecho que se ve muy claro: parecería que la mejor forma de comprender la teoría de las escalas es encarándola como la intersección de conjuntos, todos idénticos entre sí, donde cada conjunto está formado por 7 elementos distintos dispuestos en un orden determinado, y donde la cantidad de conjuntos puede tender a infinito en caso de continuar. Por eso, cuando se dice que “el proceso puede hacerse no sólo subiendo desde la escala de Do, sino también hacia abajo desde el Do hacia el Fa”, ahí, justamente ahí, se ve el error: ¿Por qué “hacia abajo”, si el FA es la 4ª nota de la escala de Do? Entonces, si habíamos empezado por DO, si después seguíamos por el RE… el MI… pues ahora le tocaría, por orden, al FA. Nada de ir “hacia atrás”. ¿Y qué sucede haciéndolo de esta otra manera? Sucede que el SIb queda “metido” en la escala de Do, así como podría ser también con el resto de los bemoles, e igualmente con los sostenidos, a medida que fuesen apareciendo todos. Y, naturalmente, cualquier nota que lleve un sostenido, o un bemol, podrá ser la fundamental (tónica) para formar una nueva escala.
Entonces la deducción general se vuelve fácil: Si en la octava pueden “caber” todos los sonidos necesarios para empezar una escala, y si entre esos mismos sonidos fundamentales también se pueden contar los sostenidos y los bemoles (escala de Do#, de Re#… o de Mib, Reb…etc), y habiendo comprobado que hay sonidos en común, eso significa que lo que tenemos es la intersección de 24 conjuntos idénticos entre sí, en un espacio acústico que contiene todos los conjuntos. Y en ese espacio puede crecer la densidad, en la medida que se sigan sumando nuevos conjuntos, y tiende a infinito. Ahí se terminaron los tetracordios y el círculo de quintas.
En el cálculo de la entonación justa, que es el que corresponde por igual a la escala de Pitágoras o la de Aristógenes – a las que vinimos refiriéndonos hasta ahora – la proyección de quintas es una sola, y se desarrolla en un espacio limitado cada vez más denso, y ese espacio es el intervalo de octava. El temperamento igual (aquél que define la separación entre todos los semitonos según la raíz doce de dos) limitará la densidad de ese espacio, mediante la adopción de 12 sonidos y sólo 12, aunque existan por lo menos 24 maneras distintas de anotar los 12 elementos.
Y cabe repasar aquí algo a propósito de esto último. El nombre de “escala cromática” que se le ha dado a la escala temperada de 12 sonidos – e incluso a las diferentes formas posibles de escribirla –, contribuye a crear no pocas confusiones. Tal como nos preguntábamos en el octavo artículo de la serie, ¿cómo demostrar de dónde viene el semitono cromático? Otro hueso duro de roer, claro está, pero es hasta que se entiende que el tal semitono viene en realidad del propio conjunto de todas las escalas diatónicas. Entonces, supongamos, si hiciéramos crecer la cantidad de conjuntos (escalas) en número suficiente, descubriríamos intervalos más pequeños que el “cromático”, dentro del mismo espacio, incluso menores que la coma, todos formados entre sonidos naturales hasta el infinito. Esto no es la teoría general del microtonalismo, porque la base de cálculo no sería aquí la subdivisión del semitono resultante de la raíz 12 de 2.
Resumiendo: el círculo de quintas y los tetracordios no sirven para razonar el origen de las tonalidades, porque desde el punto de vista matemático las notas no son términos generalizables y entonces pueden llevar a errores de concepto. Y, por otra parte, cuando los compositores y algunos teóricos dicen que “el cromatismo es un desarrollo de la tonalidad”, en realidad tienen razón – aunque ahora sabemos por fin por qué: es porque en la acústica no existen sonidos “ajenos” a las tonalidades.
Y si no existen, ¿cuál sería la tonalidad al cabo de “x” vueltas de la espiral?
Habría una sospecha muy lógica: la idea del infinito es algo tan inaprensible que cuesta imaginar que al cabo de un número suficiente de quintas justas – o sea, de una cantidad suficiente de vueltas de la espiral –, no se hallará finalmente alguna frecuencia que permitiese cerrar la proyección, siempre en base a la relación justa 3/2 definida por Pitágoras. Si esto ocurriera, querría decir que el número posible de tonalidades basadas en la quinta justa pitagórica 3/2 sería finito. ¿Será así?
Hemos visto que en cada vuelta de la espiral la diferencia con la frecuencia de la escala básica aumenta exponencialmente en una coma. Es decir, si tenemos:
o lo que es lo mismo:
donde 
o sea, una coma, y n es el exponente de la coma cada 7 octavas (o sea, al completarse cada nuevo ciclo de 12 quintas justas), la pregunta sería:
¿Llegará la parte decimal de para n tendiendo a infinito, a ser cero para algún n? O lo que es lo mismo:
¿Llegará para n tendiendo a infinito, a dar como resultado un número entero para algún n?
Y la respuesta es NO. La parte decimal del resultado de la división podrá eventualmente acercarse a cero tanto como se quiera, pero nunca será cero. Es decir, el resto de la división anterior nunca será cero.
El motivo es que, para que fuese cero alguna vez, debería cumplirse que todos los factores primos de los divisores fueran iguales uno a uno a algunos de los de los dividendos, y eso no puede pasar nunca.
En efecto, se puede demostrar por inducción:
para la primera iteración, será 
para la segunda, 
para la tercera, 
y en la iteración n será 
En una palabra, tenemos una repetición interminable del número 3 en el dividendo y otra del número 2 en el divisor. Como 3 y 2 son números primos entre sí, no hay nada más que hacer: aunque los multipliquemos hasta el infinito, el resultado de la división nunca será entero, o sea, el resto de la división, que genera la parte decimal del resultado, nunca será cero.
Esto demuestra que la cantidad de tonalidades también tiende a infinito y que la escala de Do original jamás tendrá su enarmónica equivalente exacta. Nunca, jamás, en ninguna vuelta de la espiral, llegará a aparecer la escala de DO nuevamente; llegaremos a estar muy próximos, pero, como la parte decimal nunca será cero, la enarmonía es imposible. A cada vuelta se generarán más y más tonalidades, infinitas tonalidades, de hecho, aunque sea imposible representarlas a todas con notas. Y, como corolario, ello no ocurrirá solamente con la escala de Do, sino con cualquier otra: absolutamente ninguna escala podrá tener una enarmónica exacta en el conjunto.
¿Y qué importa eso, si disponemos de la escala temperada?
Como esto es imposible de razonar con notas, conviene hacer una puntualización acerca de lo que los músicos ya saben: Una alteración cualquiera, como el sostenido, por ejemplo, equivale a modificar la frecuencia (altura de la nota) en un “semitono”. Si la alteración es “doble” (doble-sostenido, por ejemplo), la altura de la nota variará en 2 semitonos. Y, generalizando, n sostenidos equivaldrá a una cantidad n de semitonos. De ahí que escribir notas de esa manera no puede representar nunca la afinación justa de todos los sonidos deducibles por el cálculo, porque la relación de semitonos no expresa un valor exponencial, sino lineal. Por eso al principio dudábamos si estaría resuelto el problema de darle nombres a las notas “innombradas” mediante la escritura de dobles o triples alteraciones. Ahora vemos que no, que no puede ser.
Así entonces, la pregunta que hacíamos recién acerca de cuál sería la tonalidad al cabo de “x” vueltas de la espiral, importa desde otro punto de vista: siendo que el conjunto de escalas tiende a infinito, la demostración que terminamos de hacer viene también a confirmar, una vez más, que no existe sonido alguno ajeno a las tonalidades. Y esto, a su vez, demuestra la inviabilidad de la hipótesis del atonalismo (es decir, la posible ausencia de tonalidad) que se impondría en la música del siglo XX. La escala temperada y las 7 notas con sus respectivas alteraciones, que es la forma de escribirla por semitonos en el pentagrama, ha sido la base teórica para la abolición de la tonalidad, pero es una representación grosera de la realidad física si ésta es llevada hasta sus últimas consecuencias.
Desde luego que esto no significa negar la utilidad práctica de la escala temperada de 12 sonidos. Tampoco se sugiere que el oído sea capaz de distinguir diferencias tan pequeñas de frecuencias como las que se puedan deducir del cálculo, la mayoría de las cuales estarían por debajo de la percepción – de hecho, una aproximación suficiente a cero en la parte decimal permite decir que el circuito se cierra en ese punto para la percepción auditiva.
Acerca de lo que sí queremos llamar la atención es que cuando los músicos razonan exclusivamente en base a notas y alteraciones pueden caer en errores de concepto tan graves como querer fundar teorías que no resisten la prueba del cálculo matemático.
The Música y ciencia – 11 Acerca del círculo de quintas. by Gustavo Britos Zunín, unless otherwise expressly stated, is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 2.5 Spain License.
{ 19 } Comentarios
Muy denso, pero muy buen artículo, como es habitual Gustavo.
Yo creo que los que no sabían mucho de teoría musical las estarán pasando “canutas” para seguirte en estos dos últimos artículos.
Pero lo bueno es que están tan bien escritos que si los leen unas cuantas veces, pueden llegar a entender todo este jaleo musical que tenemos montado.
En mi opinión, deberíamos tener los instrumentos clásicos con afinación temperada. Basar la teoría musical actual en la escala temperada en tono de concierto.
Y dejar las demás frecuencias no usadas para nuevos tratados de teoría musical, pero que sean completamente ajenos a la teoría musical clásica.
El que quiera salirse de la escala temperada, que se invente su teoría. Que seguro que un día aparece una teoría musical más simple y más útil. Pero que no se intente adaptar la clásica, que esto ya no hay quien lo adapte, ¿no crees?
Muchas gracias por el “desasnamiento” como se viene diciendo por aquí!
Hombre, si, es otro artículo denso… pero, claro, como ya comentó Gustavo en el post anterior, si se quiere establecer la relación entre música y ciencia no hay más remedio que ser riguroso.
A mí me parece simplemente genial, cómo a partir del inicuo círculo de quintas, solamente dándole vuelta tras vuelta, cómo llega a desmontar la principal baza teórica de ciertas teorías musicales…
Genial.
La verdad es que sí, que el famoso círculo de quintas se ha tomado como referencia en muchos tratados de música. Sobre todo anglosajones por lo que yo he podido ver.
En mi escuela básicamente lo utilizamos para aprender el orden de los sostenidos en las armaduras de cada tonalidad, pero para poco más. En otros sitios se utiliza para entender conceptos de armonía, pero yo, por más que lo intento, no me facilita nada en ese aspecto.
Gracias a tí también, Macluskey, por esa aficción tuya a darle vueltas a las cosas cuando no acaban de tener sentido! Creo que gracias a ello hoy tenemos un artículo mejor todavía.
Y una pregunta para Mac, como alguien que se ha acercado hace poco a la teoría musical, pero desde tu gran experiencia como “escuchador” musical:
¿No te parece buena idea mantener afinación de concierto en los instrumentos y afinación temperada? Nos quitamos de problemas y de errores de comas, diferencias entre sostenidos y bemoles y demás parafernalias. Y creo que podemos tener una teoría musical bastante coherente hasta que tengamos otra más sencilla y más completa!
Permiteme que te felicite, otra vez, por tus artículos.
@Voro: No se merecen las gracias… yo he aprendido mucho gracias a Gustavo. Lo que pasa es que, como buen escéptico irredento que soy, intento entender bien las cosas, y con la teoría musical no he sido capaz. Hasta ahora (hasta un punto, claro).
Y sobre la pregunta que me haces… pues no sé qué decir.
En realidad la pregunta sería: ¿Purismo pitagórico a machamartillo, o practicidad?
Como ya decía Gustavo en el artículo de los griegos, si Pitágoras hubiera hecho cuadrar a la fuerza siete octavas con doce quintas, los músicos de todos los tiempos se hubieran ahorrado un montón de dolores de cabeza. Y era muy sencillo, lo tenía al alcance de la mano, sobre todo para un científico como él.
Bastaba con hacer 2^7 = (x/2)^12, y despejar x… que da 2,99661415…, y entonces decir que la quinta debía tener una frecuencia de (2,996614…/2) de la nota original, en vez de (3/2), et voilà: Desaparecen las comas y por arte de ensalmo tenemos la escala temperada, y el círculo de quintas generaría un solo conjunto de doce notas, y sólo uno, el de la escala temperada, por más vueltas que dé.
¿Con esto se perdía la “relación natural”? Vale. ¿Y qué más da?
… Porque estoy completamente convencido de que los griegos del Siglo VI A.C., que experimentaban con las cuerdas de sus liras, no serían capaces de distinguir entre una cuerda de longitud 3 y otra de longitud 2,996614, sus instrumentos de medida no tenían semejante precisión (ni sus oídos semejante agudeza).
En definitiva, la diferencia entre una quinta pitagórica “natural” y una temperada es completamente inapreciable para el común de los mortales. En la octava central del piano, la que tiene el famoso La de 440Hz, su quinta (Mi) en lugar de tener 660 Hz, que sería lo que tendría si fuera la afinación justa, tendría… ¡659,26 Hercios!. Hay quien asegura que es capaz de distinguir la diferencia. Yo no, y es más, no me creo que eso sea posible para nadie, por muy entrenado que tenga uno el oído. Yo he hecho pruebas con el Audacity, y una diferencia de una coma la distingo… a duras penas. Pero tres cuartos de hercio en 660…
O sea, que si por este ignorante fuera, sólo se usaría la afinación temperada, y se acabaron los problemas. Pero, claro…
¿Cómo se te ocurre preguntar estas cosas tan elevadas a alguien que no sabe nada de música? 
Saludos
Bueno, creo que le he preguntado a la persona correcta
Correctísima respuesta y además estoy de acuerdo contigo. Como medio músico que soy, nunca me he puesto a hacer cálculos matemáticos, aunque debería haberlos hecho!
Pero vamos, has resumido el conflicto perfectamente en un par de párrafos y has dejado la postura de la afinación temperada bien establecida.
Ahora falta alguien que nos haga entrar en razón y justifique el uso de sostenidos y bemoles “pitagóricos”.
Un placer leeros, de verdad.
Saludos,
Ahora me dispongo a afinar mi guitarra y tengo el siguiente dilema (que antes no tenía)
Empezando por la cuerda más grave (MI) voy afinando las cuerdas consecutivas con un intervalo de cuarta (MI, LA, RE, SOL, SI, MI). La única excepción es ese intervalo de tercera entre el SOL y el SI, que se hace para poder llegar al MI una octava más alta en la cuerda más aguda. O sea, que no es que sea una excepción; Yo a eso le llamo trampa directamente. En cualquier caso, con un buen oído esta afinación por cuartas debería responder a una relación dada, igual que el 3/2 de las quintas. Sin embargo, de esta manera llegamos a un MI en la cuerda aguda que no tiene exactamente el doble de frecuencia que el MI de la cuerda grave. ¿En qué cuerda se debería hacer “trampa” para que todo cuadre? Serán diferencias mínimas, pero me pregunto si eso se notará de alguna manera cuando se toca una pieza.
Y precisamente por ser diferencias mínimas, ¿por qué no suena estridente? Quiero decir, si una quinta está en relación 3/2 y suena bien por resonancia, ¿cómo es que una relación de 2,996/2 no suena horrible?
@Voro: Gracias por los cumplidos, pero, repito, yo de “hacer” música no sé absolutamente nada, sólo de escucharla y de tratar de entenderla.
Dudo que mis pobres palabras puedan servir de argumento para convencer a nadie… pero si la reflexión te ha servido… ¡me alegro muchísimo!
@Argus: Sobre lo de afinar cuerdas de guitarra (o de cualquier otra cosa)… me temo que tendrás que preguntar a alguien que sepa. No tengo ni la menor idea de cómo se afina nada (como no fuera con un medidor electrónico de frecuencias, claro, y creo que ni así).
Ahora bien, a la pregunta que haces al final:
“por ser diferencias mínimas, ¿por qué no suena estridente? Quiero decir, si una quinta está en relación 3/2 y suena bien por resonancia, ¿cómo es que una relación de 2,996/2 no suena horrible?…
…eso sí que creo que puedo responderlo, o al menos imaginármelo. Supón este escenario:
Una gran orquesta moderna, con la cuerda completa, madera cuádruple, 4 trombones y tuba, 8 trompas y cuatro trompetas, arpa, percusión… Fijémonos ahora en la cuerda: 60 profesores, de los que 30 son violines (16 primeros y 14 segundos), 12 violas, 10 cellos y 8 contrabajos.
Sale el concertino y da la orden de afinar a la orquesta. El oboe da la nota (el dichoso La de 440 Hz) y afina el viento. Vuelve a dar la nota y afina la cuerda (en ocasiones por un lado la cuerda grave y por otro los violines). Se supone que con esto todo el mundo ha afinado el La y, con ello todo el resto de notas. Es decir, todo el mundo, los 100 profesores de la orquesta, dan exactamente 440 Hz al ejecutar el La.
¿Exactamente? ¿100 personas diferentes, 440 Hz exactamente? Imposible, físicamente imposible. Centrándonos en los violines solamente, no es posible que los 30 tengan exactamente la misma tensión en las cuerdas ni en el arco, ni que los 30 profesores pongan el dedo exactamente en la misma centésima de milímetro al hacer la presa, ni que las cuerdas sean todas exactamente iguales, del mismo grosor y composición… Imposible.
Es sencillamente imposible que, en el sorprendente caso de que el La del oboe tenga 440,00000 Hz, todo el resto de la orquesta afine su La a 440,00000 Hz.
…
Ahora bien, supongamos por un momento que sí, que, por un milagro y por una vez, todos los instrumentos dan el La a la misma frecuencia exacta, hasta el quinto decimal, al afinar. ¿Qué pasaría luego, mientras se ejecuta la obra? ¿Todas y cada una de las notas que ejecutarían todos y cada uno de los profesores, decenas de miles de ellas en total, estarían perfectamente afinadas? Imposible, de nuevo. A ver cómo puedes asegurar que si un violín tiene que dar 50 DO’s en el transcurso de la obra, en todos y cada uno de ellos el dedo está exactamente en el mismo punto, haciendo la misma presión y con el mismo ángulo de ataque del arco. Multiplica ahora por 30 violines, o por 60 profesores en la cuerda, o 100 en la orquesta.
…
Pero supongamos de nuevo que sí, que por un milagro aún mayor, esto ocurre. Pues ni aun así. Porque mientras se ejecuta la obra las cuerdas se van destensando muy poco a poco, se van calentando, etc, lo justo para variar mínimamente de nuevo los hercios resultantes.
Y sin embargo… ¡suena bien, maravillosamente bien, si la orquesta es buena!
En definitiva, y perdón por el tostón, el oído tiene una serie de tolerancias a los sonidos, igual que las cuerdas las tienen al resonar, y una diferencia de un 1 o un 2 por mil es inapreciable para todo el mundo, salvo que tengas un aparatito electrónico para medir la frecuencia… pero, entonces… ¡¡¡¿dónde está la gracia???!
Un cordial saludo de este supino ignorante.
Dije antes que no tenía ni idea de afinar guitarras… ni nada, en realidad. Pero de lo que dice Argus deduzco un par de cosas:
1) El Mi final está DOS octavas por encima del Mi inicial, no una. 2) Dos octavas son 14 notas… naturales, pero son 24 semitonos, que estar, lo que se dice estar… están. Con seis cuerdas para repartir esos 24 semitonos, hay que dividir 24 semitonos entre 5 intervalos “intercordales” (si es que se dice así, que lo dudo). 24/5= 4,8. O sea, no se pueden tener 5 intervalos “intercordales” idénticos si queremos que la sexta cuerda esté afinada al cuádruple de frecuencia que la primera (o sea, dos octavas más arriba).
La mejor solución será, supongo, tener 4 intervalos entre cuerdas de 5 semitonos y uno de 4 semitonos. No será perfecto, pero es lo más aproximado. Y así es exactamente como estás afinando tu guitarra: los intervalos Mi-La; La-Re; Re-Sol y Si-Mi son de 5 semitonos, y el intervalo Sol-Si, de cuatro semitonos.
Pero claro, cuando hablas en cuartas y en terceras… yo no me entero. Porque estás mirando el pentagrama y no estás teniendo en cuenta los semitonos que hay entre notas; seguramente por eso te resultaba raro y pensabas que “hacías trampa”. Porque supongo que luego, cuando ejecutes una pieza, sí que usarás bemoles y sostenidos cuando la partitura lo pida, ¿no? Luego, aunque no se escriban (porque estás afinando en do mayor, por lo que veo), ahí están.
Definitivamente, la nomenclatura musical de segundas, cuartas, quintas y demás, basada en cómo se escriben las notas y no en cómo suenan es completamente incomprensible para los legos. Lo digo por experiencia, como buen lego que soy…
Saludos de nuevo
Argus, los dos tenéis razón (aunque Argus se haya confundido de octava).
En mi caso, yo la guitarra la afino con afinación temperada, así que las dos octavas son el cuádruple de frecuencia.
De hecho, las guitarras (al contrario que los violines) tienen trastes, así que la escala la tienen dividida en 12 sonidos de igual distancia entre ellos (a estas alturas creo que me puedo tomar esta licencia).
Lo que quiero decir, es que entiendo que TODAS las guitarras tienen afinación temperada, ya que un Do# es lo mismo que un Re bemol. Es el mismo traste.
Otra cosa es que los virtuosos se pongan a hacer un bending milimétrico para diferenciar ese sostenido del bemol y saltar la coma. Me parecería un poco ridículo tocar así, pero es como lo hacen las flautas más o menos… creo… vamos que no tengo ni idea de esto último. jejejej.
@Mac: No sólo es imposible que los 30 violines estén afinados y se toquen exactamente igual como comentas. Es que si lo estuvieran no oiríamos 30 violines sonando a la vez sino que oiríamos un violín sonando más fuerte (si despreciamos el efecto de la sala y la diferente posición y timbre de cada uno, claro).
@Argus: La disonancia sólo se empieza a apreciar a partir de cierta diferencia, si la diferencia es muy pequeña (como ocurre con los 30 violines de Mac) el resultado es bueno. Si desafinamos un poquito más cada violín empezará a sonar muy desagradable. En este hecho se basan las guitarras de 12 cuerdas, los solos a dos guitarras tan característicos de grupos como Thin Lizzy o los pedales de “chorus”. Además puedes comprobarlo tú mismo con dos cuerdas de la guitarra. Toca la misma nota en dos cuerdas y empieza a hacer un bending poco a poco en una de ellas y lo verás.
Hola a todos. Bien, creo que las cuestiones planteadas por cada uno han quedado resueltas por los mismos comentarios, lo que me dice que estos artículos van surtiendo su efecto…
@Macluskey: Ya te dije que lamentablemente no naciste en la época de Pitágoras! Esa deducción de una quinta 2,996614…./2, y que es tuya y así lo hice notar en aquel artículo, nos habría evitado unos 2500 años de dolores de cabeza.
@Voro: En realidad hace tiempo que pienso que la escritura moderna de la música debería numerar los sonidos del 1 al 12 y terminar con tantas especulaciones teóricas. Habría únicamente 12 escalas mayores y sus 12 relativas menores, todo el mundo aprendería a afinar de esa manera, y, como no habría sostenidos ni bemoles para leer, nadie sabría si el oído le “engaña” y tal vez debiera tocar una coma más alto o más bajo al tocar el sonido 2 que euivaldría tanto a Do sostenido como a Re bemol. Pero, como dije en otro artículo, el sistema de 7 notas está impreso en la mente de los músicos – y en millones de toneladas de papel también. Y el sistema sigue sirviendo. (????)
En cuanto al resultado sonoro de una imposible afinación idéntica, nota a nota, pera una orquesta de 100 músicos, esas ínfimas desafinaciones producen batimientos complejísimos originados por sonidos que no son puros (los armónicos que contiene el conjunto provienen de la mezcla de timbres de los diferentes instrumentos), de manera que eso sería lo que produciría ese timbre tan particular de los grandes conjuntos instrumentales como una orquesta sinfónica. Tal vez eso se perdiese si fuera posible hacer que todos los músicos afinasen idénticamente, y en fase, cada nota sin excepción. Es decir, supongo que podría perderse.
No se me ocurre comentar nada más sobre lo que cada uno ha dicho muy acertadamente, y muchas gracias por las apreciaciones.
Un saludo y espero que mi serie os siga gustando!
Voro, los trastes de la guitarra ofrecen una afinación temperada, pero se puede afinar la guitarra de oído sabiendo cómo suena un intervalo de 5 semitonos, que es la distancia entre una cuerda y la siguiente. Si afinamos así cuerda a cuerda, llegamos a un MI agudo que no tiene exactamente 2 octavas más -tienes razón Mac, son 2- que el MI grave.
Ahora no puedo probarlo en mi guitarra porque estoy de mudanza, pero con una guitarra eléctrica con distorsión al máximo es fácil afinar las cuerdas así, pues la distorsión exagera los pequeños fallos de afinación. Una vez afinadas, la distorsión se nota muchísimo menos y es más “redonda”. Al afinar así las cuerdas de dos en dos, se trata de ver cuánto distorsionan entre octava y octava, por ejemplo, entre la 4a cuerda en el trase 14 y la 1a cuerda al aire. Esto es el mismo MI, pero el de la cuerda 4 estaría “temperado” y el de la cuerda 1 sonaría según un ciclo de cuartas. Creo que será imperceptible, pero cuando lo pruebe os lo confirmo.
Argus, si te he entendido bien, no estoy de acuerdo contigo.
Si afinas de oído, haciendo sonar cuerdas contiguas, entiendo que lo que estás haciendo es pisar el traste 5 de la 6ª cuerda y la 5º cuerda al aire, para que suene la misma nota y afinar. Como bien dices el batimento hace desagradable el sonido simultáneo con distorsiñon así que se puede afinar de forma precisa.
El problema aquí es que al igualar la afinación de una cuerda con otra pisando traste, es que estás afinando una “cuarta” pero con afinación temperada, puesto que tomas de referencia ese 5º traste. Y las octavas serán siempre múltiplos exactos.
Espera un momento, si lo que dices al afinar haciendo sonar simultáneamente dos cuerdas al aire, entonces no te entiendo. En ese caso no se produce el batimento al desplazar la afinación un poquito más allá o más acá de una cuarta pitagórica. No entiendo como puedes asegurar de oído que estás a una cuarta justa (pitagórica) y no a 5 semitonos. Si tienes un oído capaz de diferenciar esas dos frecuencias, te envidio. Yo no soy capaz.
Y creo que la distorsión suena muy redonda en los dos casos (cuarta justa y 5 semitonos temperados). Si lo pruebas me cuentas y lo miro yo también. Pero estoy convencido.
Voro, efectivamente me refería a afinar las cuerdas haciéndolas sonar al aire. Por supuesto que no soy capaz de diferenciar una cuarta temperada de una pitagórica, faltaría más! Sólo me preguntaba si con ayuda de la distorsión se podría intentar. Pero no, no lo creo. Con lo cual, lo que deduzco de esto es que si nadie puede distinguir la diferencia, ¿quién dice que la cuarta pitagórica es la “exacta”? ¿por qué exacta? Lo mismo pasa con el círculo de quintas ¿quién dice que lo exacto es una relación 3/2 y no 2,996/2? Es como en la antigua Grecia cuando se quería pensar que PI era 22/7 ¿Es ese PI más exacto que 3,14159?
Efectivamente, Argus. ¡Ése es el quid de la cuestión!
¿Qué relación es más exacta? El tema es que si se van a uilizar 7 notas, parecería mucho más propocional y natural usar la relación 2,996/2, que deja espacios proporcionales entre todas las notas de las escalas. Y al rellenar los huecos para usar las 12 notas “cromáticas” sigue manteniendose la proporción y las exactitudes.
¿¿¿¿No os parece todavía más natural el 2,996/2 que el antiguo 3/2????
El 3/2 será muy redondo el número y tal, pero los resultados (usando 7 notas como decidieron en su momento) no son nada redondos. Son feos, inexactos, y poco útiles.
Un saludo!
El asunto de la afinación de los instrumentos es otro buen ejemplo de lo “sencillo” que es el tema de la acústica aplicada en la música. Pero los guitarristas estais de parabienes… En el piano la afinación de las octavas es bastante más complicada de lo que se podría uno imaginar, con 88 notas temperadas, triples cuerdas para casi todas las teclas, algunas con dobles cuerdas y sólo unas pocas con una cuerda sola en la región grave. Así es como ni siquiera con el temperamento igual se arreglan todos los problemas de afinación, a causa del fenómeno llamado “inarmonía”. Hay un artículo muy interesante acerca de todo esto en Wikipedia: http://es.wikipedia.org/wiki/Ac%C3%BAstica_del_piano
Desde luego Gustavo, cada vez que miro el piano por dentro me quedo más asombrado. Y ver trabajar a los afinadores es alucinante, la verdad.
Voy a ver el artículo de la Wiki.
Un saludo y gracias por el esfuerzo!!!!
Tenia yo todo un rollo montado para explicar el porqué del circulo de 5tas y la relación que guarda éste con la teoría de los tetracordios, y sumado a eso, muchas otras cuestiones que le acuñan al circulo de 5tas.
La explicación, mejor “imposible”, no puedo estar más agradecido del tiempo que le dedicó el Sr. Gustavo para redactar todo eso. Sumado a eso, los comentarios más constructivos, “imposible”, dado que en muchos de los blogs y lugares donde las personas opinan es en busca de tener la razón imponiendo “verdades” sin fundamento en sí. Debemos hacer las cosas en pro del crecimiento, no de tener la razón, la razón la dan los hechos, los resultados de las cosas hablan por sí solos.
Escribe un comentario