Tal vez estás leyendo este artículo, pero ¿estás seguro de ello? No deberías estarlo, ya que tras los meses de rigor entre artículo y artículo, hoy volvemos al nebuloso mundo de Cuántica sin fórmulas. Continuamos el bloque dedicado a los estados cuánticos en general y, en concreto, a las aplicaciones prácticas del entrelazamiento cuántico. En el último artículo de la serie hablamos acerca de una de ellas, la criptografía cuántica, mediante la cual utilizamos las borrosas propiedades del Universo para transmitir información sin que nadie se entere de lo que nos decimos.
Soy consciente de que algunos anheláis artículos más filosóficos que aquél, y tarde o temprano vendrán, pero a quienes así pensáis tengo que pediros paciencia: no tendría sentido hablar de estados y entrelazamiento sin hacerlo sobre criptografía, teletransporte, qubits o computación cuántica, si queremos dar una idea más o menos amplia sobre la mecánica cuántica actual, con lo que los alternaremos. De modo que hoy seguiremos con un asunto muy relacionado con el anterior, aunque mucho me temo que a algunos os decepcione porque los medios de comunicación suelen darle unos aires que no se corresponden con la realidad, y el propio nombre puede ser engañoso: el teletransporte cuántico.
Como digo, tanto el nombre como las descripciones que a veces se oyen por ahí –no quiero hablar sobre el nivel general de las secciones de ciencia de muchos medios o empezaría a soltar espumarajos por la boca– conducen mucho a confusión. Antes de que entremos en una descripción más detallada de lo que es el teletransporte cuántico, quiero que quede claro lo que no es: no es ni un transporte de materia ni un proceso instantáneo. ¿Ya estás decepcionado? Si no es así todavía, veamos algunas razones más para estarlo, y luego hablemos de cómo conseguir el teletransporte cuántico de manera descriptiva e inmundamente simplista –si eres físico como yo, aléjate de este artículo ahora mismo o luego vendrá el rechinar de dientes, ¡avisado estás!–.

Va a ser que no.
Cuando decimos la palabra “teletransporte”, lo que viene a la cabeza –por lo menos a la mía– es el transporte instantáneo de materia a través del espacio. Evidentemente, siempre podemos transportar materia a lugares lejanos, simplemente moviéndola, pero eso requiere tiempo y nadie lo llamaría “teletransporte”. Si hay una barrera física entre ambos lugares, por ejemplo, ya no podríamos transportarnos. De igual modo, si queremos transportar algo entre dos lugares que están a una distancia gigantesca, hacerlo mediante el movimiento requiere de un tiempo muy largo, mientras que el teletransporte –entendido, como digo, de manera intuitiva– significaría que podemos realizar el tránsito instantáneamente. Y, siguiendo este criterio, ese “teletransporte” es imposible de acuerdo con la mecánica clásica, con la relativista y la cuántica, todas por igual.
Pero imagina esta otra situación, que podríamos llamar pseudoteletransporte clásico, y que podría tener lugar si el mundo no fuera “borroso”, sino que la mecánica clásica fuera la que describe el Universo de forma completa; no es un “teletransporte verdadero”, pero no está nada mal. Supongamos que tú, estimado y valiente lector, estás tan a gusto leyendo este artículo frente a tu ordenador en vez de hacer algo más útil con tu vida, y yo consigo, de alguna manera, conocer con una exactitud absoluta la posición y velocidad de todas y cada una de las partículas fundamentales que componen tu cuerpo.
Si así fuera, y luego yo transmitiera toda esa información hasta otro lugar diferente, por ejemplo, la Estación Espacial Internacional, y allí dispusiera de los suficientes átomos de distintos elementos como para reconstruir un cuerpo humano, podría utilizar esa información que he obtenido, disponer los átomos en la estación de modo que todos y cada uno de ellos tuvieran exactamente las mismas posiciones relativas, velocidades, energías, etc., con lo que tendríamos una copia exacta e indistinguible de ti en la Estación.
A continuación, yo podría destruir tu cuerpo en tu habitación frente a tu ordenador, para que no tuviéramos la incómoda situación de que hubiera dos copias de ti, y entonces el único “tú” que existiría sería el que está en la Estación Espacial Internacional, sin que tu cuerpo se haya movido en ningún momento desde tu habitación hasta la estación. Naturalmente, existe un problema filosófico muy profundo ahí: el que está en la Estación Espacial Internacional ¿eres realmente tú? Si la configuración y estructura exacta de tus huesos, músculos, sistema nervioso con cada una de las neuronas, recuerdos, etc., son indistinguibles del original, ¿eres “tú”? Esto lleva a cuestiones mucho más profundas aún, como la propia pregunta de qué significa “tú”, en las que no vamos a entrar ahora, porque no es el objetivo de este artículo.
La cuestión es que, de este modo, habríamos logrado una suerte de “pseudoteletransporte”. Por un lado, los átomos de tu cuerpo no se han movido de su sitio, ni instantáneamente ni de ninguna otra manera. De hecho, para evitar situaciones incómodas he reducido tu cuerpo original a cenizas; además, he necesitado tener ya, en el lugar de destino, un conjunto de átomos de muchos elementos listo para recibir la información de tu cuerpo y convertirse en tu “nuevo cuerpo”. Por otro lado, el proceso no es instantáneo en absoluto: he necesitado transmitir la información desde la habitación de tu casa hasta la Estación Espacial, por ejemplo utilizando ondas de radio, y luego recibir la información allí y disponer la materia que tengo para reformar tu cuerpo de la manera adecuada. De ahí que no sea un teletransporte “de verdad”, aunque todo depende, claro está, de cómo definamos el término.
Como ves, este pseudoteletransporte es teóricamente perfectamente plausible de acuerdo con la mecánica clásica… e irrealizable en la práctica por razones obvias. Para empezar, ¿puedes imaginar la cantidad de información que requeriría transmitirse para conocer con exactitud todas las variables que definen cada una de las partículas que forman tu cuerpo? Y, aunque enlace otra vez con los aspectos filosóficos del asunto, ¿estarías dispuesto a someterte al proceso, y sentirías que quien aparecería al otro lado en la Estación eres tú mismo?
Pero este “pseudoteletransporte” mediante la transferencia de la información completa sobre un sistema físico para reconstruirlo en otro lugar no sólo es imposible en la práctica: es imposible debido a la naturaleza cuántica del Universo. No es posible conocer todas las variables de un sistema con exactitud o, lo que es lo mismo, no es posible conocer el estado de un sistema sin alterarlo. De hecho, espero que cuando hayas leído más arriba lo de “conocer con una exactitud absoluta la posición y la velocidad” hayas lanzado un gruñido de desdén; “¿Con exactitud ambas cosas a la vez? ¡Menudo atrevimiento!”, habrás pensado, y con razón. De modo que ¿cómo conseguir ese pseudoteletransporte en un mundo cuántico?

Los primeros en definir teóricamente un proceso por el cual conseguirlo fueron C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres y W. K. Wootters, en 1993, en “Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels”, publicado en 1993. No esperes que te explique con detalle el sistema de Crépeau y compañía, pero sí al menos una descripción que te dé una idea de dónde está la clave de todo el asunto. La primera vez que conseguimos llevar el sistema de estos científicos a la práctica “teletransportando” fotones fue, por cierto, cuatro años más tarde: en 1997 se publicó en Nature “Experimental Quantum Teleportation”, de D. Bouwmeester, J.-W. Pan, K. Mattle, M. Eibl, H. Weinfurter y A. Zeilinger. Eso sí, no esperes cohetes: como veremos luego, no hemos logrado aún nada que se parezca, ni de lejos, a lo que consigue Scotty en cada episodio de Star Trek.
La clave del sistema de Brassard y sus colegas es, como tal vez hayas sospechado ya, el entrelazamiento cuántico del que llevamos hablando unos cuantos artículos de la serie. Mediante el entrelazamiento es posible transmitir, de manera indirecta, el estado de una parte de un sistema sin alterarlo, midiendo por el contrario otra parte del sistema que esté entrelazada con él, como hicimos en el caso de la criptografía cuántica del último artículo.
Supongamos el caso de un sistema físico más sencillo que el de tu cuerpo; de hecho, supongamos un caso muy, muy sencillo, el de un sistema físico con dos autoestados, como un electrón que puede tener el espín hacia arriba o hacia abajo, un fotón que puede estar polarizado horizontal o verticalmente o, ya que ésos son ejemplos mundanos y aburridos, el de un cuantejo que puede resultar ser zanahoriófilo o zanahoriófobo cuando le muestras una zanahoria, e intentemos teletransportarlo en el Universo cuántico. Tal vez, como en artículos anteriores, pueda hacerte falta papel y lápiz, porque la cosa va a volverse liosa (si no fuera así, me estaría quedando en la superficie que suele leerse por ahí, con lo que este artículo no aportaría nada). Eso sí, mi explicación, como suele suceder, es bastante pobre, y mira que lo intento aclarar… de modo que, de antemano, disculpas por los líos en los que voy a meterte.
No voy a insultar tu inteligencia repitiendo todas las propiedades de los cuantejos que explicamos en el artículo de criptografía. Supongamos que tu cuantejo está en un estado cualquiera que es una superposición de los dos estados propios, $a \left | zanahori\acute{o}filo \right \rangle + b \left | zanahori\acute{o}fobo \right \rangle$, donde $a$ y $b$ tienen que ver, como hemos visto en la serie, con la probabilidad de que al mostrarle esa verdura el cuantejillo se lance a por ella o se ponga a llorar.

Sí, mucho me temo que los cuantejos han vuelto.
Antes de nada –porque si no entiendes esto, nada de lo que viene después tiene sentido–, veamos por qué no puedes hacer lo mismo que si el mundo no fuera cuántico; ¿por qué no puedes simplemente mostrarle una zanahoria al cuantejo, ver si es zanahoriófilo o zanahoriófobo, llamar por radio a la Estación Espacial y comunicárselo y punto final? Si te haces esa pregunta, permite primero que te dé un pescozón, porque eso significa que no has asimilado la serie hasta ahora. Si le enseñas una zanahoria a tu cuantejo, claro que su estado va a colapsarse a $\left | zanahori\acute{o}filo \right \rangle$ o $\left | zanahori\acute{o}fobo \right \rangle$… Pero si eso es lo que comunicas a la Estación Espacial y ellos preparan un cuantejo idéntico al que tienes tú después de mostrarle la zanahoria, lo que tienen no es idéntico al cuantejo original.
Para entender esto, en el resto del artículo supondremos un estado concreto para tu cuantejillo –un estado que tú y yo, por supuesto, desconocemos si no realizamos ninguna medición sobre el cuantejo enseñándole una zanahoria–, de modo que no haya unas $a$ y $b$ abstractas. Imaginemos pues que tu cuantejo está en el estado $\frac{1}{2}\left | zanahori\acute{o}filo \right \rangle + \frac{\sqrt{3}}{2}\left | zanahori\acute{o}fobo \right \rangle$, es decir, es bastante más probable que al enseñarle la zanahoria se muestre zanahoriófobo que zanahoriófilo. Si esto te suena muy raro, te recomiendo que releas el artículo sobre superposiciones cuánticas, por cierto.
¿Ves cómo enseñarle una zanahoria al cuantejo y luego comunicar el resultado a la Estación no resuelve el problema? Esto es lo que sucedería:
- Tú tienes $\frac{1}{2}\left | zanahori\acute{o}filo \right \rangle + \frac{\sqrt{3}}{2}\left | zanahori\acute{o}fobo \right \rangle$.
- Enseñas una zanahoria al cuantejo, y éste se pone a llorar, luego su estado se ha colapsado a $\left | zanahori\acute{o}fobo \right \rangle$.
- Llamas por radio a la Estación Espacial Internacional, y les comunicas que el estado del cuantejo es $\left | zanahori\acute{o}fobo \right \rangle$.
- Ellos de algún modo preparan a su cuantejo para que también lo sea, con lo que tienen un cuantejo en el estado $\left | zanahori\acute{o}fobo \right \rangle$.
¡No hemos teletransportado el cuantejo original! Hemos obtenido una cosa diferente, pues el proceso ha modificado el cuantejo inicial. De hecho, como puedes ver, este pseudoteletransporte funcionaría sólo para cuantejos que están en uno de los autoestados, porque entonces la información a transmitir es trivial y se trata de un caso casi idéntico al clásico.
Pero, si el cuantejo está en un estado que no es trivial y que no conocemos, como por ejemplo $\frac{1}{2}\left | zanahori\acute{o}filo \right \rangle + \frac{\sqrt{3}}{2}\left | zanahori\acute{o}fobo \right \rangle$, ¿cómo teletransportar ese cuantejillo a otro lugar como la Estación sin modificar su estado, de modo que al otro lado tengamos un cuantejo indistinguible de ése sin llevarlo físicamente hasta la Estación?
Lo primero que nos hace falta, además de tu cuantejo (el original que queremos pseudoteletransportar), es otro par de cuantejos más. Porque la clave de la cuestión es utilizar el entrelazamiento cuántico para convertir el cuantejo de la Estación en una copia indistinguible del tuyo – a efectos prácticos, en tu mismo cuantejo.
De modo que, en primer lugar, producimos un par de cuantejillos entrelazados como explicamos al hablar de criptografía, de modo que estén siempre en estados opuestos. Tú te quedas en tu casa con uno de ellos, al que llamaremos Orejitas, y yo me voy a la Estación con el otro cuantejo, Canela. Y unos días después intentamos realizar nuestro experimento con un cuantejo más, Chispas. Nuestro objetivo es que Chispas acabe en la Estación Espacial conmigo, o un cuantejo indistinguible de Chispas, claro.
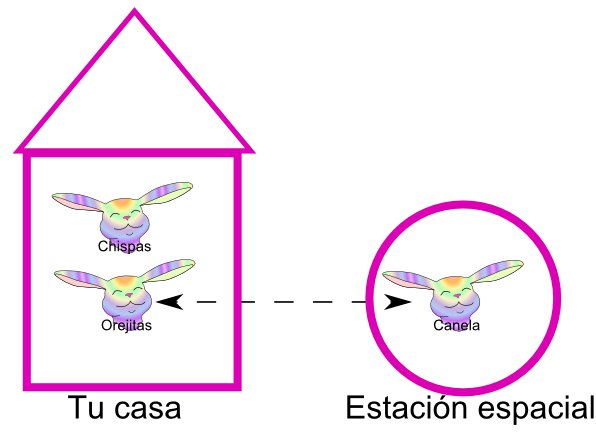
Situación inicial (Orejitas y Canela están entrelazados).
Y, aunque sea repetitivo, recuerda: si realizas una medición sobre Chispas, _entonces dejará de ser Chispa_s como era antes y habremos fastidiado todo el asunto, porque lo que me mandarías sería sólo parte de la información sobre Chispas, de manera que yo sería incapaz de recrear a Chispas tal y como era. Pero esto merece una pausa, porque es una de las dos claves de todo el asunto (y me disculpo de nuevo si lo estás entendiendo tan bien que estas pausas te resultan aburridas).
La razón de que el teletransporte no pueda funcionar a la manera clásica es que lo que quiera que queremos transportar –Chispas, un fotón, un átomo de sodio– no es completamente cognoscible. Si medimos absolutamente algunas de sus propiedades, por el principio de incertidumbre de Heisenberg perdemos otras, con lo que no es posible convertir el sistema en información a la antigua usanza, transferir esa información y luego reconstruir el sistema en el punto de destino con la información transmitida.
En términos de Chispas, nuestro simple cuantejillo tiene una “personalidad” en lo que a las zanahorias se refiere, una personalidad que nos es imposible conocer completamente: $\frac{1}{2}\left | zanahori\acute{o}filo \right \rangle + \frac{\sqrt{3}}{2}\left | zanahori\acute{o}fobo \right \rangle$. La única manera de conocer parte de su personalidad es mostrarle una zanahoria –medir–, pero entonces sólo tenemos una parte de la información sobre él, y la otra parte se ha perdido y nunca podremos recuperarla de nuevo.
Nuestro sistema, que es el del teletransporte cuántico, salvará ese obstáculo haciendo uso del entrelazamiento, mediante el cual hay una conexión íntima entre Orejitas y Canela, una conexión que transmite el estado de uno al otro de manera instantánea y sin que haya necesidad de que lo conozcamos nosotros. Lo que haríamos sería lo siguiente:
-
Entrelazamos a Chispas con Orejitas. Para ello, en el caso de los cuantejos, metemos a ambos en una misma caja durante cierto tiempo, y en el caso de sistemas físicos reales… bueno, depende. Estos experimentos suelen hacerse con fotones, que pueden llevarse junto con otros fotones a través de láminas semiespejadas y “combinarse” para formar estados entrelazados diversos. El caso es que, en los absurdos términos de nuestra analogía, ahora Orejitas y Chispas son amigos.
-
Medimos el estado conjunto de Chispas y Orejitas, mostrándoles una zanahoria. Una vez hemos hecho esto, no hay vuelta atrás: Chispas ya no es el que era antes, hemos colapsado el estado Chispas + Orejitas y sólo hemos obtenido parte de la información que queremos transmitir. Si no hubiéramos hecho nada más, nuestro experimento sería un fracaso, porque la parte de la información sobre Chispas que no hemos obtenido se habría perdido. Para seguir con nuestra analogía, ya que conocemos algo sobre Chispas pero no todo, imaginemos que ahora sabemos que Chispas tenía mayor probabilidad de ser zanahoriófobo que de ser zanahoriófilo, es decir, sabemos que $b > a$. Y ya nunca podremos saber, mirando a Chispas, qué valores tenían ni $a$ ni $b$.
-
Aquí es donde está lo genial del sistema desarrollado por Bennet, Jozsa, Wootters y compañía. Al entrelazar a Chispas con Orejitas, éste contiene parte de la información de Chispas, y por tanto la misma información –o más bien la opuesta– está en Canela, en la Estación Espacial. Aunque se escapa con mucho al nivel de este artículo, de modo que tendrás que creerme, la parte de la información original que se queda en Orejitas y, a través de él, en Canela, es justo la información que no hemos obtenido al hacer la medición.
Es decir, ahora Canela “se parece” a Chispas, pero puede no ser exactamente igual que él. En términos de nuestro ejemplo, supongamos que tras la medición Canela puede acabar en uno de estos dos estados: $\frac{\sqrt{3}}{2}\left | zanahori\acute{o}filo \right \rangle + \frac{1}{2}\left | zanahori\acute{o}fobo \right \rangle$ o $\frac{1}{2}\left | zanahori\acute{o}filo \right \rangle + \frac{\sqrt{3}}{2}\left | zanahori\acute{o}fobo \right \rangle$. Supongamos que hay un 50% de probabilidades de que Canela haya quedado en uno u otro estado, con lo que es incluso posible que ya sea exactamente igual que Chispas, o tal vez no. Y recuerda también que nosotros no conocemos el estado de Canela ni esos números, ya que no lo hemos “medido”.
-
Tenemos, por tanto, el estado original de Chispas “partido” en dos pedazos: por un lado, información que conocemos nosotros explícitamente, al haber mostrado la zanahoria a Chispas + Orejitas, a saber, que Chispas es más zanahoriófobo que zanahoriófilo. Por otro lado, información contenida en Canela, un cuantejo sobre el que no hemos realizado medición ni modificación alguna todavía, que es el hecho de que Canela está en uno de los dos estados que he escrito un poco más arriba. De modo que, para que yo pueda disponer de toda la información, implícita y explícita, hace falta que me envíes un mensaje con lo que has visto al enseñar la zanahoria a Chispas + Orejitas, por ejemplo, mediante una llamada de radio. Tú me llamas a la Estación y me dices, “Pedro, he enseñado zanahorias a los cuantejillos y mi conclusión es que Chispas es más zanahoriófobo que zanahoriófilo”.
-
Finalmente, utilizando la información que me has enviado, yo modifico a Canela. Por ejemplo, lo “entreno” para que si su probabilidad de ser zanahoriófilo era menor que la de ser zanahoriófobo se quede como estaba, pero si era al revés intercambie los coeficientes de zanahoriófilo y zanahoriófobo. En la realidad, claro está, hablamos de cosas como fotones, de modo que puede hacerse pasar el fotón por un sistema físico que asegure, por ejemplo, que la componente horizontal de la polarización del fotón sea mayor que la vertical si no era así.
Observa que mi entrenamiento de Canela consiste básicamente en “decirle”: si ya eres más zanahoriófobo que zanahoriófilo, quédate como estás. Si es al revés, intercambia ambas probabilidades, pero no estoy enseñando ninguna zanahoria a Canela. No he medido nada sobre él, luego no se ha colapsado ni a $\left | zanahori\acute{o}filo \right \rangle$ ni a $\left | zanahori\acute{o}fobo \right \rangle$.
Supongamos que, en nuestro caso particular el estado de Canela era $\frac{\sqrt{3}}{2}\left | zanahori\acute{o}filo \right \rangle + \frac{1}{2}\left | zanahori\acute{o}fobo \right \rangle$. Tras el entrenamiento, el cuantejillo habrá comprendido que debe intercambiar ambos coeficientes, pues quiero que sea más zanahoriófobo que zanahoriófilo al igual que Chispas, de modo que se modifica hasta convertirse en $\frac{1}{2}\left | zanahori\acute{o}filo \right \rangle + \frac{\sqrt{3}}{2}\left | zanahori\acute{o}fobo \right \rangle$… es decir, en Chispas.

La situación final (los dibujos de Chispas y Orejitas sólo tratan de mostrar que ya han sido medidos).
Si los ojos aún no te dan vueltas, recapitulemos lo que hemos conseguido: hemos logrado tener en la Estación a un cuantejillo exactamente idéntico a Chispas. Recuerda que, si la cuántica es una teoría completa, cuando el estado de dos sistemas es el mismo estado no es sólo que tengamos la misma información de ambos, sino que ambos sistemas son idénticos en sí mismos, es decir, quien está en la Estación ya no es “Canela” sino “Chispas”, porque todo lo que hace a Chispas ser Chispas, sin excepción, está en él. A cambio, nuestro Chispas original ya no es Chispas – su estado se ha colapsado a otra cosa. Hemos “pseudoteletransportado” a Chispas.
Observa que todas las limitaciones del pseudoteletransporte clásico siguen presentes aquí: hace falta un cuantejo en el destino antes de “transportar” nada, y hace falta transmitir información a la manera clásica –en nuestro caso, cuando me llamas por radio– para completar el proceso, ya que la información transmitida por el entrelazamiento entre Orejitas y Canela es sólo una parte del total. De modo que no estamos cerca, ni mucho menos, de transportarte a ti u objetos similarmente complejos: la cantidad de información necesaria, como en el caso anterior, es increíblemente grande.
Otra limitación, en este caso una que no existía de igual modo en el método clásico, es el hecho de que, como verás, hemos tenido dos cuantejos entrelazados en tu casa y la Estación. Pero, en la práctica, mantener el entrelazamiento sin que se produzcan interacciones con el entorno que acaben con ella es muy difícil, sobre todo si es durante un tiempo o distancias largas.

Diagrama del teletransporte cuántico de fotones bajo el Danubio.
Hasta ahora hemos logrado “teletransportar” de este modo fotones y unos pocos átomos, pero cuanto más complejo es el sistema a transportar, menor distancia hemos conseguido. Con fotones, en 2004 se logró el teletransporte cuántico bajo el río Danubio y una distancia de unos 600 metros, utilizando una fibra óptica para transmitir los fotones entrelazados –si alguien conoce un experimento más reciente de mayor distancia, decídmelo y actualizamos el artículo–; con átomos, tan sólo de unas cuantas micras. De manera que hacerlo con algo tan sumamente complejo como, qué se yo, una taza de café está todavía muy lejos, y lograrlo distancias que merezcan la pena, todavía más: porque, si vas a utilizar una tecnología compleja y carísima para “transportarte” unos cuantos cientos de metros, mejor te montas en el autobús.
En el próximo artículo atacaremos un asunto un poco más filosófico apoyándonos en éste; observa que hoy, en cierto sentido, hemos obtenido información de algo sin medirlo, a través del entrelazamiento entre Orejitas y Canela. En la siguiente entrada de la serie exploraremos más en detalle cómo utilizar esta peculiaridad del entrelazamiento para saber cuándo algo está ahí sin mirarlo, algo que parece justo lo contrario de lo que sugiere la mecánica cuántica (que suele involucrar no poder ver cosas que están ahí aunque las miremos), hablando sobre el detector de bombas de Elitzur-Vaidman.
Si no has saltado a este último párrafo sino que te has leído el ladrillo entero, me quito el sombrero. Eso sí, no lo comentes con las personas de tu entorno o puedes encontrarte aislado socialmente en menos que canta un gallo. Y, si ves un cuantejo por ahí, busca ayuda inmediatamente.
Puedes encontrar este artículo y otros como él en el número de abril de 2010 de nuestra revista electrónica, disponible a través de Lulu:
Para saber más (esp/ing cuando proceda):

